Asking If the Existence of Vacuum Energy to Keep Computational “Bits” Present at Start of Cosmological Evolution, Even If Spatial Radius Goes to Zero, Not Planck Length, Is Possible ()
Received 10 December 2015; accepted 15 April 2016; published 18 April 2016

1. Introduction
This article is to investigate what happens physically if there is a non-pathological singularity in terms of Einsteins equations at the start of space-time. This eliminates the necessity of having then put in the Planck length since then they would be no reason to have a minimum non-zero length. The reasons for such a proposal come from [1] by Stoica who may have removed the reason for the development of Planck’s length as a minimum safety net to remove what appears to be unadvoidable pathologies at the start of applying the Einstein equations
at a space-time singularity, and are commented upon in this article. 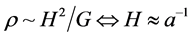 in particular is re-
in particular is re-
marked upon. This is a counter part to Fjortoft theorem in Appendix I. The idea is that entanglement entropy will help generate bits, due to the presence of a vacuum energy, as derived at the end of the article, and the presence of a vacuum energy non-zero value, is necessary for comsological evolution. Before we get to that creation of what is a necessary creation of vacuum energy conditions, we refer to constructions leading to extremely pathological problems which [1] leads to minus the presence of initial non-zero vacuum energy. [2] also adds more elaboration on this.
Note a change in entropy formula given by Lee [3] about the inter relationship between energy, entropy and temperature as given by
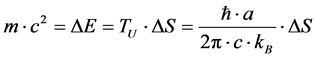 (1)
(1)
As a reviewer has asked about Equation (1) and the inter relationship of a mass m, and acceleration, the key point of this review is to look at if gravitons have a mass, m, in the beginning, and if Equation (1) is used, which the mass of a graviton is proportional to the following
 (1a)
(1a)
The reason why the mass of a graviton is stated as given by Equation (1a) is to presume that the relationship given by Lee [3] , as to any mass, is given by Equation (1) and Equation (1a), so we can relate any presumed
mass linked to gravitons to change in entropy. As to acceleration appearing, the acceleration, 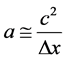 is part
is part
of the formula given by Equation (1) and by default Equation (1a) and also by thermodynamic reasoning the generalized temperature
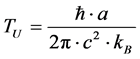 (1b)
(1b)
If we assume, in the onset of expansion of the universe, that Equation (1b) holds, then we can review the application of Equation (1a) to graviton mass, m, as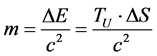 , and to have acceleration, given by
, and to have acceleration, given by 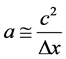 as part of a definition of generalized temperature, given by Equation (1b).
as part of a definition of generalized temperature, given by Equation (1b).
Note that temperature is, in this presentation by Lee [3] presumably a constant initially, i.e. very hot, so then we are really in this presentation, assuming that the acceleration as given by 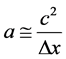 is a constant, so in fact what we are actually reviewing through Equation (1a) is a direct relationship of mass as proportional to entropy, i.e. as
is a constant, so in fact what we are actually reviewing through Equation (1a) is a direct relationship of mass as proportional to entropy, i.e. as
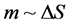 (1c)
(1c)
i.e. the mass of a graviton is presumed to be proportional to entropy, i.e. in choosing Equation (1c) we are leading up to one of the themes of this document which is that if entropy is proportional to information and note that later, we will be relating entropy, as given, to a numerical count factor, i.e. then in fact, this will lead to a re write of Equation (1c) to read as, if N (count) is a numerical count proportional to the change in Entropy, that
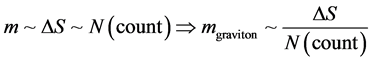 (1d)
(1d)
This assumes that we are evaluating Equation (1b) as a constant, i.e. that the temperature be fixed, which is leading to the acceleration, which the referee was so concerned about, as a constant, i.e. via the relationship of
looking at ![]() as an acceleration factor, and presumably that the delta x factor in acceleration is of the interval of Planck length.
as an acceleration factor, and presumably that the delta x factor in acceleration is of the interval of Planck length.
Lee’s formula is crucial for what we will bring up in the latter part of this document. Namely that changes in initial energy could effectively vanish if [1] is right, i.e. Stoica removing the non pathological nature of a big bang singularity. That is, unless entanglement entropy is used.
If the mass m, i.e. for gravitons is set by acceleration (of the net universe) and a change in enthropy ![]() between the electroweak regime and the final entropy value of, if
between the electroweak regime and the final entropy value of, if ![]() for acceleration is used, so then we obtain
for acceleration is used, so then we obtain
![]() (2)
(2)
Then we are really forced to look at (1) as a paring between gravitons (today) and gravitinos (electro weak) in the sense of preservation of information.
Having said this note by extention![]() . As
. As ![]() changes due to
changes due to ![]() and
and![]() , t hen a is also altered i.e. goes to zero.
, t hen a is also altered i.e. goes to zero.
What will determine the answer to this question is if ![]() goes to zero if
goes to zero if ![]() which happens if there is no minimum distance mandated to avoid the pathology of singularity behavior at the heart of the Einstein equations. In doing this, we avoid using the energy
which happens if there is no minimum distance mandated to avoid the pathology of singularity behavior at the heart of the Einstein equations. In doing this, we avoid using the energy ![]() situation, i.e. of vanishing initial space-time energy, and instead refer to a nonzero energy, with
situation, i.e. of vanishing initial space-time energy, and instead refer to a nonzero energy, with ![]() instead vanishing. In particular, the Entanglement entropy concept as presented by Muller and Lousto [4] is presented toward the end of this manuscript as a partial resolution of some of the pathologies brought up in this article before the entanglement entropy section. No matter how small the length gets,
instead vanishing. In particular, the Entanglement entropy concept as presented by Muller and Lousto [4] is presented toward the end of this manuscript as a partial resolution of some of the pathologies brought up in this article before the entanglement entropy section. No matter how small the length gets, ![]() if it is entanglement entropy, will not go to zero. The requirement is that the smallest length of time, t, rescaled, does not go to zero. This preserves a minimum non-zero
if it is entanglement entropy, will not go to zero. The requirement is that the smallest length of time, t, rescaled, does not go to zero. This preserves a minimum non-zero ![]() vacuum energy, and in doing so keep non zero amounts of initial bits, for computational bits cosmological evolution even if
vacuum energy, and in doing so keep non zero amounts of initial bits, for computational bits cosmological evolution even if![]() .
.
I think that the common confusion here, is that ![]() refers to initial RADII and not to curvature, which was also one of the questions raised by the referee.
refers to initial RADII and not to curvature, which was also one of the questions raised by the referee. ![]() is a minimum radii and has nothing to do with curvature. This formula, which evidently confused referees, i.e. if
is a minimum radii and has nothing to do with curvature. This formula, which evidently confused referees, i.e. if ![]() refers to a computational bits value which will show up in our manuscript, then our statement is that we have an initial radii of less than Planck Length. As given by
refers to a computational bits value which will show up in our manuscript, then our statement is that we have an initial radii of less than Planck Length. As given by
![]() (2a)
(2a)
Is part of the build up of Equation (3) and should be read by readers so as to understand the significance of what is in this Equation (2a). I.e. ![]() does not hold, in general, and we get Equation (2a) only if the
does not hold, in general, and we get Equation (2a) only if the ![]() value is used which refers to a computational bits value.
value is used which refers to a computational bits value.
Before doing that, we review Ng [5] and his quantum foam hypothesis to give conceptual underpinnings as to why we later even review the implications of entanglement Entropy.
We state unequivocally here, that Equation (2a) has ![]() referring to a computational bits value which is Equation (3) and will be part of treating entropy and its evolution
referring to a computational bits value which is Equation (3) and will be part of treating entropy and its evolution
Note that this evaluation is preformed in the Planck time interval, and is the basis of evaluation by our paper.
I.e. the concept of bits and computations is brought up because of applying energy uncertainty, as given by [5] and the Margolis theorem appears to indicate that the universe could not possibly evolve if [1] is applied, in a 4 dimensional closed universe. This bottle neck as indicated by Ng’s [5] formalism is even more striking in the author’s end of article proof of the necessity of using entanglement entropy in lieu of the conclusion involving
entanglement entropy, which can be non zero, even if ![]() provided there is a minimum non-zero time length.
provided there is a minimum non-zero time length.
2. Review of Ng, [5] with Comments
First of all, Ng refers to the Margolus-Levitin theorem with the rate of operations ![]()
![]() . Ng wishes to avoid black-hole formation
. Ng wishes to avoid black-hole formation![]() . This last step is not important to our view point, but we refer to it to keep fidelity to what Ng brought up in his presentation. Later on, Ng refers to the
. This last step is not important to our view point, but we refer to it to keep fidelity to what Ng brought up in his presentation. Later on, Ng refers to the ![]() with
with ![]() the Hubble radius. Next Ng refers to the
the Hubble radius. Next Ng refers to the![]() . Each bit energy is
. Each bit energy is ![]() with
with ![]()
The key point as seen by Ng [4] and the author is in
![]() (3)
(3)
Assuming that the initial energy E of the universe is not set equal to zero, which the author views as impossible, the above equation says that the number of available bits goes down dramatically if one sets ![]() ? Also Ng writes entropy S as proportional to a particle count via N.
? Also Ng writes entropy S as proportional to a particle count via N.
![]() (4)
(4)
We rescale ![]() to be
to be
![]() (5)
(5)
The upshot is that the entropy, in terms of the number of available particles drops dramatically if ![]() becomes larger.
becomes larger.
So, as ![]() grows smaller, as
grows smaller, as ![]() becomes larger.
becomes larger.
a) The initial entropy drops;
b) The nunber of bits initially available also drops.
The limiting case of (4) and (5) in a closed universe, with no higher dimensional embedding is that both would almost vanish, i.e. appear to go to zero if ![]() becomes very much larger. The quest4ion we have to ask is would the number of bits in computational evolution actually vanish?
becomes very much larger. The quest4ion we have to ask is would the number of bits in computational evolution actually vanish?
3. Does It Make Sense to Talk of Vacuum Energy If ![]() Is Changed to
Is Changed to ![]() ? Only Answerable Straightforwardly If an Embedding Superstructure Is Assigned. Otherwise Difficult, Unless One Is Using Entanglement Entropy Which Is Non Zero Even If
? Only Answerable Straightforwardly If an Embedding Superstructure Is Assigned. Otherwise Difficult, Unless One Is Using Entanglement Entropy Which Is Non Zero Even If ![]()
We summarize what may be the high lights of this inquiry leading to the present paper as follows:
a. One could have the situation if ![]() of an infinite point mass, if there is an initial nonzero energy
of an infinite point mass, if there is an initial nonzero energy
in the case of four dimensions and no higher dimensional embedding even if [1] goes through verbatim. The author sees this as unlikely. The infinite point mass construction is verbatim if one assumes a closed universe, with no embedding superstructure and no entanglement entropy. Note this appears to nullify the parallel Brane world construction used by Durrer [6] . The author, in lieu of the manuscript sees no reason as to what would perturb this infinite point structure, so as to be able to enter in a big bang era. In such a situation, one would not have vacuum energy unless entanglement entropy were used. That is unless one has a non zero entanglement entropy
[4] present even if![]() . See [7] for a smilar argument.
. See [7] for a smilar argument.
b. The most problematic scenario. ![]() and no initial cosmological energy. i.e. this in a 4 dimensional closed universe. Then there would be no vacuum energy at all. initially. A literal completely empty initial state, which is not held to be viable by Volovik [8] .
and no initial cosmological energy. i.e. this in a 4 dimensional closed universe. Then there would be no vacuum energy at all. initially. A literal completely empty initial state, which is not held to be viable by Volovik [8] .
c. If additional dimensions are involved in beginning cosmology, than just 4 dimensions will lead to physics which may give credence to other senarios. One scenario being the authors speculation as to initial degrees of freedom reaching up to 1000, and the nature of a phase transition from essentially very low degrees of freedom, to over 1000 as speculated by the author in 2010 [9] .
The relevant template for examinging such questions is given in Table 1 as printed.
e. The meaning of octonionic geometry prior to the introduction of quantum physics presupposes a form of embedding geometry and in many ways is similar to Penrose’s cyclic conformal cosmology speculation.
f. It is striking how a semiclassical argument can be used to construct in Table 1. In particular, we look at how Planck’s constant is derived, as in the electroweak regime of space-time, for a total derivative [11] [12]
![]() (6)
(6)
Similarly [11] [12]
![]() (7)
(7)
The A field so given would be part of the Maxwell's equations given by [10] as, when ![]() represents a D’Albertain operator, that in a vacuum, one would have for an A field [11] [12]
represents a D’Albertain operator, that in a vacuum, one would have for an A field [11] [12]
![]() (8)
(8)
And for a scalar field ![]()
![]() (9)
(9)
Following this line of thought we then would have an energy density given by, if ![]() is the early universe permeability [11]
is the early universe permeability [11]
![]() (10)
(10)
We integrate (10) over a specified E and M boundary, so that, then we can write the following condition namely [11] [12] .
![]() (11)
(11)
(11) would be integrated over the boundary regime from the transition from the octonionic regime of space time, to the non-octonionic regime, assuming an abrupt transition occurs, and we can write, the volume integral as representing [11] [12]
![]() (12)
(12)
Then by applying [11] [12] we get ![]() formed by semiclassical reasons. In semiclassical reasoning similar to [10] .
formed by semiclassical reasons. In semiclassical reasoning similar to [10] .
![]()
Table 1. Time interval dynamical consequences does QM/WdW apply?
![]() (Constant value) (13)
(Constant value) (13)
The question we can ask, is that can we have a prequantum regime commencing for (11) and (12) for ![]() if
if![]() ? And a closed 4 dimensional universe? If so, then what is the necessary geometrial regime
? And a closed 4 dimensional universe? If so, then what is the necessary geometrial regime
of space-time so that the integration performed in (11) can commence properly? Also, what can we say about the formation of (12) above, as a number, ![]() gets larger and larger, effectively leading to. Also, with an octonionic geometry regime which is a pre quantum state [13] .
gets larger and larger, effectively leading to. Also, with an octonionic geometry regime which is a pre quantum state [13] .
In so many words, the formation period for ![]() is our pre-quantum regime. Table 1 could even hold if
is our pre-quantum regime. Table 1 could even hold if ![]() but that the 4 dimensional space-time exhibiting such behavior is embedded in a higher dimensional template. That due to
but that the 4 dimensional space-time exhibiting such behavior is embedded in a higher dimensional template. That due to ![]() not removing entanglement entropy as is discussed near the end of this article.
not removing entanglement entropy as is discussed near the end of this article.
4. If ![]() Then If There Is an Isolated, Closed Universe, There Is a Disaster Unless One Uses Entanglement Entropy
Then If There Is an Isolated, Closed Universe, There Is a Disaster Unless One Uses Entanglement Entropy
One does not have initial entropy, and the number of bits initially disappears. That is if one is not using entanglement entropy, as will be examined at the end of this article.
Abandoning the idea of a completely empty universe, this unperturbed point of space time (of matter-energy) appears to be a configuration for a static point of space time with no perturbation, as may be the end result of applying Fjortoft theorem [14] to the thermodynamic potential as given in [15] , i.e. the non definitive answer for fulfillment of criteria of instability by applying Fjortoft’s theorem [14] to the potential [15] leading to no instability as given by the potential given in [15] may lead to a point of space-time with no change, i.e. a singular point with “infinite” mass which does not change at all. This issue will be reviewed in [16] a different procedure, i.e. a so called nonsingular universe construction. To get there we will first of all review an issue leading up to implementation of [16] .
5. Can an Alternative to a Minimum Length Be Put in? Consider the Example of Planck Time as the Minimal Component, Not Planck Length
From J. Dickau, [17] the following was given to the author, as a counter point to ![]() leading to a disaster.
leading to a disaster.
“If we examine the Mandelbrot Set along the Real axis, it informs us about behaviors that also pertain in the quaternion and octonic case-because the real axis is invariant over the number types. If numbers larger than.25 are squared and summed recursively (i.e. ?z = z^2 + c ) the result will blow up, but numbers below this threshold never get to infinity, no matter how many times they are iterated. But once space-like dimensions are added-i.e. an imaginary compoent―the equation blows up exponentially, faster than when iterated.
Dickau concludes:
“Anyhow there may be a minimum (space-time length) involved but it is probably in the time direction”.
This is a counter pose to the idea of minimum length, looking at a beginning situation with a crucial parameter ![]() even if the initial time step is “put in by hand”. First of all, look at [4] , if E is M, due to setting c = 1, then
even if the initial time step is “put in by hand”. First of all, look at [4] , if E is M, due to setting c = 1, then
![]() (14)
(14)
Everything depends upon the parameter ![]() which can go to zero. We have to look at what (14) tells us, even if we have an initial time step for which time is initially indeterminate, as given by a redoing of Mitra’s
which can go to zero. We have to look at what (14) tells us, even if we have an initial time step for which time is initially indeterminate, as given by a redoing of Mitra’s ![]() formula [7] which we put in to establish the indeterminacy of the initial time step if quantum processes hold.
formula [7] which we put in to establish the indeterminacy of the initial time step if quantum processes hold.
![]() (15)
(15)
What Dickau is promoting is, that the Mandelbrot set, if applicable to early universe geometry, that what the author wrote, with ![]() potentially going to zero, is less important than a
potentially going to zero, is less important than a
minimum time length. The instability issue is reviewed in Appendix II for those who are interested in the author’s views as to lack proof of instability. It uses [15] which the author views as THE reference as far as thermodynamic potentials and the early universe.
6. Muller and Lousto Early Universe Entanglement Entropy, and Its Implications: Solving the Spatial Length Issue, Provided a Minimum Time Step Is Preserved in the Cosmos, in Line with Dickau’s Suggestion
We look at [4]
![]() for a time dependent horizon radius
for a time dependent horizon radius ![]() in cosmology (16)
in cosmology (16)
Equation (16) above was shown by the author to be fully equivalent to
![]() (17)
(17)
i.e.
![]() (18)
(18)
So, then one has
![]() (19)
(19)
No matter how small the length gets, ![]() if it is entanglement entropy, will not go to zero. The requirement is that the smallest length of time, t, re scaled does not go to zero. This preserves a minimum non zero
if it is entanglement entropy, will not go to zero. The requirement is that the smallest length of time, t, re scaled does not go to zero. This preserves a minimum non zero ![]() vacuum energy, and in doing so keep the non zero initial bits, for computational bits contributions to evolving space time behavior even if
vacuum energy, and in doing so keep the non zero initial bits, for computational bits contributions to evolving space time behavior even if![]() .
.
7. Reviewing a Suggestion as to How to Quantify the Shrinkage of the Scale Factor and Its Connections with Entanglement Entropy
We are given by [16] if there is a non singular universe, a template as to how to evaluate scale factor a against time scaled over Planck time, with the following results.
![]() (20)
(20)
Two time and scale factor values in tandem particularly stand out. Namely,
![]() (21)
(21)
Also
![]() (22)
(22)
The main thing we can take from this, is to look at the inter-relationship of how to pin down an actual initial Hubble “constant” expansion parameter, where we look at:
![]() (23)
(23)
Recall that![]() , which is predicated upon, if the time is close to Planck time the initial maximal density of
, which is predicated upon, if the time is close to Planck time the initial maximal density of
![]() (24)
(24)
And length given by
![]() (25)
(25)
So (24) is implying that the amount of matter in a region of space ![]() is initially about
is initially about
![]() (26)
(26)
Using 1 GeV/c2 = 1.783×10−27 kg means that (26) above is
![]() (26a)
(26a)
Then if
![]() (27)
(27)
It will lead to
![]() (28)
(28)
Then, to first order, one is looking at initial entropy to get a non zero but definite vacuum energy as leading to an entanglement entropy of about (just before the electro weak regime) regardless of the situation being in fidelity , or lack of with the physics of [18]
![]() (29)
(29)
8. Reviewing the Geometry for Embedding (29) above
In line with Stoica [1] shrinking the minimum length and referring to both (29) and (27), the idea is to use a surface area treatment as to getting the initial entropy values as given in (29). To do so, the author at the situation presented in Figure 1.
The two branes presented in Figure 1 given at ![]() and
and ![]() refer to the two Brane world states, especially in line with [19] [20] . The first one, namely
refer to the two Brane world states, especially in line with [19] [20] . The first one, namely ![]() is the Brane where our physical universe lives in, and is embedded in. If one uses this construction, with higher dimensions than just 4 dimensions, then it is possible to have a single point in 4 dimensional space as a starting point to a tangential sheet which is part of an embedding in more than 4 dimensions. Along the lines of having a 4 dimensional cusp with its valley (lowest) point in a more than 4 dimensional tangential surface. The second Brane is about
is the Brane where our physical universe lives in, and is embedded in. If one uses this construction, with higher dimensions than just 4 dimensions, then it is possible to have a single point in 4 dimensional space as a starting point to a tangential sheet which is part of an embedding in more than 4 dimensions. Along the lines of having a 4 dimensional cusp with its valley (lowest) point in a more than 4 dimensional tangential surface. The second Brane is about ![]() centimeters away from the Brane our physical world lives in, and moves closer to our own Brane in the future, leading to a slapping of the two Branes together about a trillion years ahead in our future [19] [20] . The geometry we are referring to with regards to embedding is in the first Brane
centimeters away from the Brane our physical world lives in, and moves closer to our own Brane in the future, leading to a slapping of the two Branes together about a trillion years ahead in our future [19] [20] . The geometry we are referring to with regards to embedding is in the first Brane![]() . [6] uses this geometry to have graviton production which the author has used to model Dark Energy.
. [6] uses this geometry to have graviton production which the author has used to model Dark Energy.
![]()
Figure 1. As adopted from Reference [6] .
9. Conclusion: Making Computational Bits, via (19)
As stated by Ng. the idea would be to have to give imputs into (3) i.e.
![]() (3)
(3)
Here in this case, even if the spatial contribution, due to [1] goes to zero, the idea would be to have the time length non-zero so as to have a space-time version of l non-zero. This would also be in tandem with calling E, in (3) as proportional to![]() , where if the time is Planck time, in minimum value, and
, where if the time is Planck time, in minimum value, and ![]() in value, one would have before the electro-weak an input into E, which would require an entropy (entanglement).
in value, one would have before the electro-weak an input into E, which would require an entropy (entanglement).
What remains to be seen is, if there is a geometric sheet in more than 4 dimensions, allowing for non-zero time, as argued for![]() , even if the spatial component goes to zero, according to [1] . We suggest an update as to what was written by Seth Lloyd [21] with
, even if the spatial component goes to zero, according to [1] . We suggest an update as to what was written by Seth Lloyd [21] with
![]() (30)
(30)
when [22]
![]() (31)
(31)
While doing this, a good thing to do, would be to keep in mind the four dimensional version of vacuum energy as given by Park, [23] namely
![]() (32)
(32)
As well as the transition given by a combination of [23] , with [24] , Barvinskey et al.
![]() (33)
(33)
Quantifying the above, and giving it experimental proof, via detector technology may allow us to investigate an old suggestion by the author as to four dimension and five dimensional vacuum energy which are given for
small time values![]() ,
, ![]() and for temperatures sharply lower than
and for temperatures sharply lower than![]() , Beckwith [22] (2007), where for a positive integer n
, Beckwith [22] (2007), where for a positive integer n
![]() (34)
(34)
In particular, the author is interested in investigating if the following is true.
Look at an argument provided by Thanu Padmanabhan [25] , leading to the observed cosmological constant value suggested by Park [22] . Assume that![]() , but that when we make this substitution that
, but that when we make this substitution that ![]() [26]
[26]
![]() (35)
(35)
i.e. looking at if
![]() (36)
(36)
Now to make it more interesting.
We can replace ![]() by
by![]() . In addition, we may look at inputs from the initial value of the Hubble parameter to get the necessary e folding needed for inflation, according to
. In addition, we may look at inputs from the initial value of the Hubble parameter to get the necessary e folding needed for inflation, according to
![]() (37)
(37)
Leading to
![]() (38)
(38)
If we set ![]() implying a very large initial cosmological constant value, we get in line with what Park suggested for times much less than the Planck interval of time at the instant of nucleation of a vacuum state
implying a very large initial cosmological constant value, we get in line with what Park suggested for times much less than the Planck interval of time at the instant of nucleation of a vacuum state
![]() (39)
(39)
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 110752.
Appendix I. Fjortoft Theorem
A necessary condition for instability is that if ![]() is a point in space time for which
is a point in space time for which ![]() for any given potential U, then there must be some value
for any given potential U, then there must be some value ![]() in the range
in the range ![]() such that
such that
![]() (1)
(1)
For the proof, see [12] and also consider that the main discussion is to find instability in a physical system which will be described by a given potential U. Next, we will construct in the boundary of the EW era, a way to come up with an optimal description for U.
Appendix II. Constructing an Appropriate Potential for Using Fjortoft Theorem in Cosmology for the Early Universe Cannot Be Done. We Show Why
To do this, we will look at Padamanabhan [15] and his construction of (in Dice 2010) of thermodynamic potentials he used to have another construction of the Einstein GR equations. To start, Padamanabhan [15] wrote
If ![]() is a so called Lovelock entropy tensor, and
is a so called Lovelock entropy tensor, and ![]() a stress energy tensor
a stress energy tensor
![]() (1)
(1)
We now will look at
![]() (2)
(2)
![]()
So happens that in terms of looking at the partial derivative of the top (1) equation, we are looking at
![]() (3)
(3)
Thus, we then will be looking at if there is a specified ![]() for which the following holds.
for which the following holds.
![]() (4)
(4)
What this is saying is that there is no unique point, using this ![]() for which (4) holds. Therefore, we say there is no official point of instability of
for which (4) holds. Therefore, we say there is no official point of instability of ![]() due to (3). The Lagrangian structure of what can be built up by the potentials given in (3) with respect to
due to (3). The Lagrangian structure of what can be built up by the potentials given in (3) with respect to ![]() mean that we cannot expect an inflection point with respect to a
mean that we cannot expect an inflection point with respect to a
2nd derivative of a potential system. Such an inflection point designating a speed up of acceleration due to DE exists a billion years ago [37] . Also note that the reason for the failure for (4) to be congruent to Fjoroft’s theorem is due to
![]() (5)
(5)
Appendix III. Details as to Forming Crowell’s Time Dependent Wheeler De Witt Equation, and Its Links to Worm Holes
This will be to show some things about the worm hole we assert the instanton traverses en route to our present universe. From Crowell [38]
![]() (1)
(1)
This has when we do it![]() , and frequently
, and frequently![]() , so then we can consider
, so then we can consider
![]() (2)
(2)
In order to do this, we can write out the following with regards to the solutions to Eqn (1) put up above.
![]() (3)
(3)
And
![]()
![]() (4)
(4)
This is where ![]() and
and ![]() refer to integrals of the form
refer to integrals of the form ![]() and
and![]() . It
. It
so happens that this is for forming the wave functional permitting an instanton forming, while we next should consider if or not the instanton so farmed is stable under evolution of space time leading up to inflation. We argue here that we are forming an instanton whose thermal energy is focused into a wave functional which is in the throat of the worm hole up to a thermal discontinuity barrier at the onset, and beginning of the inflationary era.
Appendix IV. The D’Albembertain Operation in an Equation of Motion for Emergent Scalar Fields
We begin with the D’Albertain operator as part of an equation of motion for an emergent scalar field. We refer to the Penrose potential ( with an initial assumption of Euclidian flat space for computational simplicity) to account for, in a high temperature regime an emergent non zero value for the scalar field ![]() due to a zero effective mass, at high temperatures. [27]
due to a zero effective mass, at high temperatures. [27]
When the mass approaches far lower values, it, a non zero scalar field re appears.
Leading to ![]() as a vanishingly small contribution to cosmological evolution
as a vanishingly small contribution to cosmological evolution
Let us now begin to initiate how to model the Penrose quintessence scalar field evolution equation. To begin, look at the flat space version of the evolution equation
![]() (1)
(1)
This is, in the Friedman?Walker metric using the following as a potential system to work with, namely:
![]() (2)
(2)
This is pre supposing![]() , that one is picking a curvature signature which is compatible with an open universe.
, that one is picking a curvature signature which is compatible with an open universe.
That means ![]() as possibilities. So we will look at the
as possibilities. So we will look at the ![]() values. We begin with.
values. We begin with.
![]() (3)
(3)
We find the following as far as basic phenomenology, namely
![]() (4)
(4)
![]() (5)
(5)
The difference is due to the behavior of![]() . We use
. We use ![]() ~axion mass
~axion mass ![]() in asymptotic limits with
in asymptotic limits with
![]() (6)
(6)
Appendix V. Interesting Speculation. Does There Exist a Five Dimensional Version of an Instanton in the Worm Hole Transition Regime?
We will attempt to build the contribution as to a Reissner-Nordstrom metric embedded in a five dimensional space-time metric, and see if this satisfied. i.e. look at (1) below This allows us to determine, using of the Risessner-Nordstrom metric as given, by Kip Thorne, Wheeler, and Misner [39] , for an added cosmological “constant” ![]() and “charge” Q. This will be shown to lead to [40]
and “charge” Q. This will be shown to lead to [40]
![]() (1)
(1)
To do this, we start off with the following space time line metric in five dimensions. This is a modification of Wesson’s book. [40]
![]() (2)
(2)
We claim that what is in the ![]() brackets is just the Reissner-Nordstrom line metric in four dimensional space. The parameters in the
brackets is just the Reissner-Nordstrom line metric in four dimensional space. The parameters in the ![]() bracket are linked to the Reissner-Nordstrom metric via
bracket are linked to the Reissner-Nordstrom metric via
![]() (3)
(3)
And
![]() (4)
(4)
And this is assuming that ![]() as well as using
as well as using ![]() with a maximum value topped off by a Planck’s length value due to
with a maximum value topped off by a Planck’s length value due to![]() . So being the case, we get the following stress tensor values
. So being the case, we get the following stress tensor values
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Furthermore, we get the following determinant value
![]() (8)
(8)
All these together lead to (1) being satisfied. Let us now see how this same geometry contributes to a worm hole bridge and a solution as to forming the instanton flux wave functional between a prior to a present universe. The Reissner-Nordstrom metric permits us to have a radiation dominated ‘matter’ solution whose matter ‘contribution’ drops off rapidly as the spatial component of geometry goes to zero. This is in tandem with radiation pressure and density falling off rapidly, as we leave the center of such a purported soliton/ instanton. This is extremely useful because it ties in with the notion of fractional branes contributing to entropy calculations. In fact it is useful to state that these two notions dove tail with each other quite closely. The only difference is that the construction above does not in itself lend to the complexity of what we would observe, which is in itself a multiple?joined net work of charge centers and of shifting geometry.
Appendix VI. Basic Physics of Achieving Minimum Precision in CMBR Power Spectra Measurements
Begin first of all looking at
![]() (1)
(1)
This leads to consider what to do with
![]() (2)
(2)
Samtleben et al. [31] consider then what the experimental variance in this power spectrum, to the tune of an achievable precision given by
![]() (3)
(3)
![]() is the fraction of the sky covered in the measurement, and
is the fraction of the sky covered in the measurement, and ![]() is a measurement of the total experimental sensitivity of the apparatus used. Also
is a measurement of the total experimental sensitivity of the apparatus used. Also ![]() is the width of a beam, while we have a minimum value of
is the width of a beam, while we have a minimum value of ![]() which is one over the fluctuation of the angular extent of the experimental survey.
which is one over the fluctuation of the angular extent of the experimental survey.
i.e. contributions to ![]() uncertainty from sample variance is equal to contributions to
uncertainty from sample variance is equal to contributions to ![]() uncertainty from noise. The end result is
uncertainty from noise. The end result is
![]() (4)
(4)
Appendix VII. Vacuum Fluctuations Which May Occur: Cosmological Perturbation Theory and Tensor Fluctuations (Gravity Waves)
Durrer reviews how to interpret ![]() in the region where we have
in the region where we have![]() , roughly in the region of the Sachs-Wolf contributions due to gravity waves. We begin first of all by looking at an initial perturbation, using a scalar field treatment of the ‘ Bardeen potential’
, roughly in the region of the Sachs-Wolf contributions due to gravity waves. We begin first of all by looking at an initial perturbation, using a scalar field treatment of the ‘ Bardeen potential’ ![]() This can lead us to put up, if
This can lead us to put up, if ![]() is the initial value of the Hubble expansion parameter
is the initial value of the Hubble expansion parameter
![]() (1)
(1)
And
![]() (2)
(2)
Here we are interpreting A = amplitude of metric perturbations at horizon scale, and we set![]() , where
, where ![]() is the conformal time, according to
is the conformal time, according to ![]() = physical time, where we have a as the scale factor.
= physical time, where we have a as the scale factor.
Then for![]() , and
, and![]() , and a pure power law given by
, and a pure power law given by
![]() (3)
(3)
We get for tensor fluctuation, i.e. gravity waves, and a scale invariant spectrum with ![]()
![]() (4)
(4)
Appendix VIII
Beginning of quote from [28]
4. Re-examining relic gravitational wave models as to what relic Gravitational waves could tell us about the origins of the early universe. As given in an earlier paper by the Author
Quoting from [9] we write the following. We reproduce this, because of the centrality of Equation (27) which is basic. It is very noticeable that in [10] we have that the following quote is particularly relevant to consider, in lieu of our results
Quote
“Thus, if advanced projects on the detection of GWs will improve their sensitivity allowing to perform a GWs astronomy (this is due because signals from GWs are quite weak) [1] , one will only have to look the interferometer response functions to understand if General Relativity is the definitive theory of gravity. In fact, if only the two response functions (2) and (19) will be present, we will conclude that General Relativity is definitive. If the response function (22) will be present too, we will conclude that massless Scalar-Tensor Gravity is the correct theory of gravitation. Finally, if a longitudinal response function will be present, i.e. Equation (25) for a wave propagating parallel to one interferometer arm, or its generalization to angular dependences, we will learn that the correct theory of gravity will be massive Scalar-Tensor Gravity which is equivalent to f(R) theories. In any case, such response functions will represent the definitive test for General Relativity. This is because General Relativity is the only gravity theory which admits only the two response functions (2) and (19) [4] [8] . Such response functions correspond to the two “canonical” polarizations h+ and h×. Thus, if a third polarization will be present, a third response function will be detected by GWs interferometers and this fact will rule out General Relativity like the definitive theory of gravity”.
End of quote
We argue that a third polarization in Gravitational waves from the early universe may be detected, if there is proof positive that in the pre Planckian regime that the Corda conjecture [11] as given below, namely if the following analysis is part of our take on relic gravitational waves, is supported by the kinetic energy being larger than the potential energy, namely what if.
Quote
“The case of massless Scalar-Tensor Gravity has been discussed in [4] [13] with a “bouncing photons analysis” similar to the previous one. In this case, the line-element in the TT gauge can be extended with one more polarization, labelled with Φ (t + z), i.e. …”.
End of quote: This ends our recap of the section given in [9] which we think is important
What we are arguing for is that the choice of the vacuum energy as given by Equation (27) may give conclusive proof as to satisfy the Corda conjecture and his supposition as to the existence of an additional polarization [10] . We will, in the future try to extend our results so as to determine if Equation (27) either falsifies or supports the existence of a 3rd polarization. Which will be a way to determine the final disposition of GR as THE theory of Cosmology, or open up the possibility of alternate theories. It is an issue which we think will require extreme diligence. While ending our query as to the possible existence of a third polarization we should mention what would be the supreme benefit of our upcoming analysis of Equation (27), namely how to avoid the conflating of dust, with gravitational waves, i.e. the tragic Bicep 2 mistake [11] - [14] .
End of quote from reference [29] which answers questions as to cosmological questions as to what is necessary for physics interpretation of both bicep 2, and the relative strength of polarization
End of quote from [28] from our present reference listing
We now go to [31] directly. It is important that the information transfer and the mathematics thereof be in fidelity to requirements as of [31] directly. If they do not lead to falsifiable results pertinent to [32] then the supposition advanced in this paper are null and void and should be not continued.