Received 4 June 2015; accepted 3 April 2016; published 6 April 2016

1. Introduction
There are many types of eruptive variables. They range from the ones which display rapid, irregular increases in brightness, as though the novae, to the spectacular supernovae. Also, there are the eruptive variable stars which show sudden, unpredicted decreases in brightness.
The most famous of the eruptive variables is the novae. The term nova means new. Actually, a nova is an existing star that suddenly emits an outburst brought a star luminosity up to naked eye visibility. It seemed like a new star. The Chinese astronomers called them guest stars. Novae, before and after their outburst, are hot subdwarf stars. They are heavenly bodies of very high temperature but small size [2] .
A typical nova flares up during its outburst to thousands or even tens of thousands of times its normal luminosity. Among the more spectacular of the cataclysms of nature is the supernova. In contrast to an ordinary nova, a supernova is a star that flares up to hundreds of millions of times its former brightness [2] .
The three most famous supernovae to have been observed during the last ten centuries in the Milky Way are, the supernova of 1054 in Taurus, the Tycho’s star of 1572 in the constellation Cassiopecia, and the supernova of 1604 in Serpens, describe by both Kepler and Galileo. In a typical Galaxy, supernovae appear to occur at the rate of at least one every few hundred of years [2] . The question is: how a star of large mass knows that it must discard a large part of its mass? or in other words, what is the mechanism by means of the massive stars lose mass?
2. Radiation Pressure
In order to make an appropriate treatment of the stability of a star, it is necessary to take account of a phenomenon which may have an important effect on the star’s equilibrium, viz. the pressure of radiation [3] . It is well known that electromagnetic waves, including light waves, posses mass and momentum and exert a force on anything which obstructs their progress [3] .
Ordinarily the pressure of radiation is extremely minute, but inside a star the radiation is so intense that the pressure is by no means negligible as regards the conditions of equilibrium of the material. As it is well kown the radiation pressure is proportional to the fourth power of the temperature, that is to say
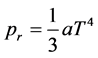 (1)
(1)
where a = 7.64 ´ 10−15 is Stefan’s constant [4] .
The outward flowing radiation may thus be compared to a wind blowing through the star and helping to distend it against gravity. The proportions of the weight of the material are borne by the radiation pressure, the remainder being supported by the gas pressure. The proportion between them is the same at all parts of the star. It does not depend on the density nor on the coefficient of opacity. This is so, since for a given flow of radiation, transparent matter offers less obstruction and experiences less force than opaque matter. But this is compensated because the flow of radiation increases with the transparency of the material [3] . It depends only on the mass and the average molecular weight.
However, it is necessary to take into account the self-generated magnetic field as a fundamental element for the star’s equilibrium [4] . As it is well known, a magnetic field has the property of generating in a conducting fluid a magnetic viscosity that confers to it a certain rigidity. That rigidity in the conducting stellar fluid may be interpreted as if the star were supported by a superstructure made up by the magnetic line as of force. It can be assumed that this magnetic superstructure has the mission of keeping the shape of the star even when this object should be animated by a rotation movement, since the magnetic lines of force are frozen in the stellar fluid and move along with it [4] .
2. The Self-Generated Magnetic Field
In the theoretical frame developed by A.S. Eddington [3] a new hypothesis was introduced by the author, which consists of proposing that at an early stage of their evolution, all gaseous stars generate an intense magnetic field whose mission is to contribute to their stability and equilibrium [4] .
In order to determine the dynamic state of a viscous and conducting compressible gaseous fluid, that moves with velocity v(x, t) in some region of space where a magnetic field H (x, t) exist, the following equations are used [4]
 (2)
(2)
and
 (3)
(3)
where p (x, t) is the total pressure, r(x, t) the mass density and h, z the coefficients of viscosity [5] . The relation (3) is the momentum balance equation of magneto hydrodynamics. For any gaseous star, the mass density is in general, a function of time t and the radius R such that r = r(R, t) [4] .
It can be directly shown that (3) takes the following equivalent form
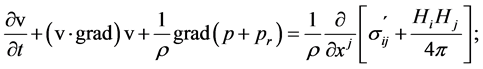 (4)
(4)
where  is the viscosity stress tensor [4] [5] , the relation of equivalence [5]
is the viscosity stress tensor [4] [5] , the relation of equivalence [5]
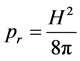 (5)
(5)
and the following well known formula in vector analysis
 (6)
(6)
were used, after integration by parts and taking in to account the condition (2). Suppose that the star revolves in such a way that the flux of the stellar fluid is steady; and then ¶v/¶t = 0. In this case it is fulfilled that
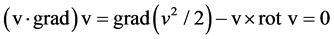 (7)
(7)
This is so, because the star revolves on its own axis with a velocity v(l, t), with l the stellar latitude, and then, v is independent of x [6] . In that case, it can be obtained that
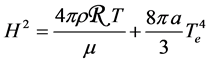 (8)
(8)
where Te is the effective temperature.
On the other hand is easy to see that in the inner regions of a given star, the first term is greater than the second one, and therefore that term can be neglected.
Consequently and for any inner region of the star, the magnitude of the magnetic field can be calculated from the following equation
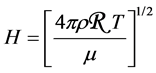 (9)
(9)
In (8) and (9), R is the gases universal constant [4] .
At the surface of the star, the mass density is practically zero, and then, the magnitude of the magnetic field can be obtained from the next relation
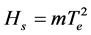 (10)
(10)
where
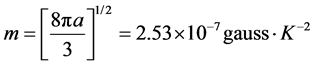 (11)
(11)
is a universal constant [4] .
3. The Mass-Luminosity Relation
From the modified mass-luminosity relation [4]
 (12)
(12)
where L is the luminosity, M the mass, G the universal gravitational constant, c the velocity of light in the empty space, a = 2.5 is a constant, and kc is the coefficient of opacity at the stellar center, and according to the theoretical frame developed by A.S. Eddington [3] it can be shown that, in general, the more massive stars are also the more luminous. The relation between the mass and luminosity of a star is not accidental or mysterious but results from fundamental laws that govern the internal structure of the stars [3] .
The mutual gravitational attraction between the masses of various regions within a star produces tremendous forces that tend to collapse the star forward its center. Thus, the central temperature must adjust itself against the gravitational pressure.
Gravitation is the force drawing matter together, and a sit gathers in more and more material tends to build stars of enormous size. It can be assumed that, opposed to this, the radiation pressure is the main disruptive force. In fact, it is known that a star without radiation pressure is stable. But since it is observed, the stellar masses cease abruptly when radiation pressure becomes important [3] . It is only when the mass has reached 1033 gm. that this check on the aggregating power of gravitation emerges from insignificance; but with further increase of mass it rapidly rises [3] .
On the other hand, and given that the lines of force of the self-generated magnetic field can be interpreted as the superstructure that gives not only a very important support to the star, but also has the mission to contribute to their stability, that internal magnetic superstructure prevens that the star from gravitational collapse or exploding because of the added effect of radiation pressure and those of hot gases.
In some way, the magnetic lines of force behave in the inner part of the star as a powerful shock absorber acting in both ways: against gravitational compression as well as against hot gases and radiation expansion.
However, the hot gases pressure depends on the temperature; that is to say
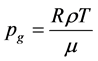 (13)
(13)
in the meantime, the magnitude of the self-generated magnetic field inside the star, is proportional to the square root of the temperature, as can be seen from Equation (9). Then, and according to (1), the radiation pressure is the dominant term; so that, the radiation inside a massive star is so intense that the pressure make up that it explode, as a nova or a supernova. The magnitude of the out burst will be depend on the amount of the stellar mass. On the other hand, in the process of the star’s formation, the mass accumulation is limited by the action from radiation pressure.
Normally, after ejecting perhaps a hundred-thousandth of its mass in a nova outburst, a star returns in the course of a few decades to its prenova state, sometime without any absorption or emission lines in its spectrum, and eventually shows only minor, irregular variations [1] . There is some indication that many nova-like stars and ordinary novae are binary systems, in which one component is small and hot while the other is large and cool. In such binaries, the large and cool star often expels gas that becomes trapped by the small and hot star. When the amount of trapped gas exceeds a certain limit, the hot star causes it to erupt in the form of a nova. Merle F. Walker, working at the Mount Wilson Observatory, made the surprising discovery that the nova DQ Herculis is an eclipsing binary star [1] . There is only one other known case of a nova in a binary system.
However this does not rule out the posibility that many novae may have close companions that would be very difficult to detect [1] .
4. Nova Herculis
The light curve of Nova Herculis contains small, strictly rhythmic oscillations whose period is 71 sec., with a very striking degree of precision. The strict periodicity suggest that the nova is pulsating like a Cepheid variable, but far more rapidly, since it contracts and expands in a cycle of only 71 seconds [1] . As it is well known, for all pulsating stars, the period in days multiplied by the square root of the average mass density is a constant [3] . The period-mass density relation for variable stars of the Cepheid type is [5]
 (14)
(14)
where b is a parameter of the theory which is used to determine the stellar mass [1] [5] . It can be assured that the relation (14) is also valid for Nova Herculis; in such a way that it is fulfilled that
![]() (15)
(15)
Let’s consider the variable star called d Cepheid. The mean density of that star is 3.42 ´ 10−4 gm∙cm−3, and its period, 5.37 days. On the other hand, the period of Nova Herculis is equal to 8.2 ´ 10−4 days; so that, and according to (15) the mean density of the nova is 15,000 gm∙cm−3.
Applying the relation (14) to Nova Herculis it is obtained that
![]() (16)
(16)
Therefore, from (16) the following values are obtained
![]() (17)
(17)
For gaseous stars the value of the mass is determined from the quadric equation [1] [2]
![]() (18)
(18)
where m = 2.11 is the average molecular weight, and the symbol indicates the mass of the Sun, which is equal to 1.985 ´ 1033 gm [1.5] so that,
![]() (19)
(19)
The value of the radius R is given by the following expression in terms of rm and M
![]() (20)
(20)
Then, and with the values of the mean density and the stellar mass, it is obtained that
![]() (21)
(21)
There can be no doubt that Nova Herculis resembling a white dwarf due to their extremely density. On the other hand, their strict periodicity suggests that it is a pulsating star like a Cepheid variable. However, it is small, hot, and an extremely dense star.
Inconsequence, it can be assured that Nova Herculis is a recurrent nova that resembling a white dwarf, and also behaves as a pulsating star like a Cepheid variable. It is well known that ordinary nova outburst recurring phenomena. The amount of mass which is lost in a single outburst is quite small, about 10−5 of the mass of the star [1] . Perhaps, this is so because in the novae their enormous density plays an important role as an opposed additional factor against the radiation pressure.
5. Conclusions
As regards the conditions of equilibrium of a star, it is necessary to take account the radiation pressure. The formulae from the theory enable in to calculate what proportion of the weight of the stellar mass is borne by the radiation pressure, and what part being supported by the hot gases pressure. To a first approximation, the proportion is the same at all parts of the star. It depends on the mass and the average molecular weight, and not on the density nor the coefficient of opacity [3] . The stars differ in brightness, density and other conditions, but they mostly contain about the same amount of material. The majority are between 1033 gm and 1034 gm. where the serious challenge of radiation pressure to compete with hot gases pressure is beginning [3] . Apparently, nature has a standard model before her forming the stars, and would not tolerate much deviation.
It can be seen in a general way, the causes of that uniformity. The force of gravitation drawing matter together tends to build stars of a very big size. However, it gathers more and more material the temperature inside the star increases their value in order to maintain the equilibrium; and that fact made that the radiation pressure increases their value too. Given that is the dominant term over the other equilibrium conditions; the hot gases pressure, and the magnitude of the self-generated magnetic field, that phenomenon is the main disruptive force. It is a significant fact that stellar masses congregate just at the point where radiation pressure is beginning to endanger the safety of the star. In consequence, the radiation pressure is the agent which has cloven chaos into the stars [3] . Radiation pressure not only limitate the mass accumulation but would be a serious danger for the stability of the stars; so that the more massive the star the smaller the chance of survival [3] .
Finally, if it is considered that laws of physics as are presently known, are valid for the Primeval Atom, sometimes also called the Cosmic Egg. It is also possible to propose that the enormous radiation pressure which generates inside of it by the extreme initial conditions of pressure, mass density, temperature, etc., is the mechanism used by nature, in order to initiate the evolutionary phenomenon known as the Expansion of the Universe, in the most fantastic and catastrophic explosion called by G. Gamow, The Big Bang.