On Common Fixed Point Theorem of Four Self Maps in a Fuzzy Metric Space ()
Received 27 January 2016; accepted 28 March 2016; published 31 March 2016

1. Introduction
L. Zadeh’s [1] investigation of the concept of fuzzy set in the year 1965, has led to a rich growth of fuzzy mathematics. Today, it has become a well-accepted system to embrace upon uncertainties springing in numerous physical situations. The theory of fixed point equations is one of the extrusive basic tools to exploit various physical formulations. Theorems on fixed points in fuzzy mathematics are emerging with flourishing hope and vital certainty.
Many authors have introduced the concept of fuzzy metric space in various ways and have shown that every metric induces a fuzzy metric. There have been several endeavors to formulate fixed point theorems in fuzzy mathematics. In 1975, Kramosil and Michalek [2] generalized the statistical metric space and defined the fuzzy metric space which was later modified by George and Veeramani [3] [4] by introducing the concept of continuous t-norms. Recently, many researchers [5] - [9] have enormously developed the theory by studying various aspects of the theory and extending the concept of fuzzy metric through applying several contractive, expansive, continuity and compatibility conditions on the fuzzy metric and producing different results.
Pant [10] introduced the notion of reciprocally continuous mappings and established a fixed point theorem. S. N. Mishra, Nilima Sharma, S. L. Singh [11] defined z-asymptotically commuting maps in fuzzy metric spaces which may be seen as a comparable formulation given by Trivari-Singh [12] in metric spaces. These mappings are more general than commuting and weakly commuting maps.
The aim of this paper is to show that the self maps in a fuzzy metric space satisfying certain properties and inequalities possess a common fixed point which is unique.
2. Preliminaries
Here, we shall recall some prefaces:
Definition 2.1 ( [13] ): A binary operation 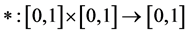 is said to a continuous t-norm if
is said to a continuous t-norm if 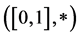 is an abelian topological monoid with unit
is an abelian topological monoid with unit  whenever
whenever  &
& 
 .
.
2.1(α) Basic continuous t-norms are:
・ 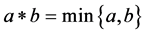 (minimum t-norm)
(minimum t-norm)
・ 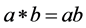 (product t-norm)
(product t-norm)
・  (Lukasiewicz t-norm)
(Lukasiewicz t-norm)
・ 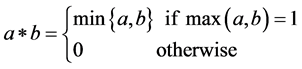 (weakest t-norm, the drastic product)
(weakest t-norm, the drastic product)
Definition 2.2 ( [3] ): Let X be any non-empty set, 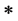 is a continuous t-norm and M is a fuzzy set on X × X × (0, ∞) satisfying
is a continuous t-norm and M is a fuzzy set on X × X × (0, ∞) satisfying
a) 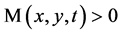
b)  Û
Û 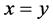
c) 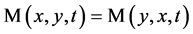
d) ![]()
e) ![]() is continuous where
is continuous where![]() ,
, ![]()
Here, ![]() denotes the degree of nearness between x, y with respect to “t”.
denotes the degree of nearness between x, y with respect to “t”.
・ Grabiec ( [14] ) had shown that ![]() is non-decreasing
is non-decreasing![]() .
.
Definition 2.3 ( [3] ): A sequence ![]() in a fuzzy metric space
in a fuzzy metric space ![]() said to converge to
said to converge to ![]() Û
Û ![]() as
as![]() .
.
Definition 2.4 ( [3] ): A sequence ![]() in a fuzzy metric space
in a fuzzy metric space ![]() is said to be a Cauchy sequence if for each
is said to be a Cauchy sequence if for each![]() ,
, ![]() , there exists
, there exists ![]() such that
such that ![]() for all
for all![]() .
.
Definition 2.5 ( [3] ): If every Cauchy sequence in a fuzzy metric space X is convergent, then X is said to be complete.
Definition 2.6 ( [10] ): Two self maps A and B of a fuzzy metric space ![]() are said to be reciprocally continuous on X if
are said to be reciprocally continuous on X if
![]() and
and ![]()
whenever ![]() is a sequence in X such that
is a sequence in X such that
![]() and
and ![]()
for some![]() .
.
Definition 2.7 ( [11] ): Two self maps A and B of a fuzzy metric space X are said to be z-asymptotically commuting if and only if
![]()
whenever ![]() is a sequence in X such that
is a sequence in X such that
![]()
for some ![]() and
and![]() .
.
Lemma 2.8 ( [14] ): Let ![]() be a fuzzy metric space. If there exists
be a fuzzy metric space. If there exists ![]() such that
such that ![]() for all
for all ![]() and t > 0, then
and t > 0, then![]() .
.
Succeeding the Grabiec’s approach to fuzzy contraction principle, Mishra. S. N., Nilima Sharma, Singh. S. L. [11] had obtained common fixed point theorem for asymptotically commuting maps in fuzzy metric spaces.
Theorem 2.9 ( [11] ): Let ![]() be a complete fuzzy metric space with
be a complete fuzzy metric space with![]() ,
, ![]() and
and ![]() . If there exist continuous maps
. If there exist continuous maps ![]() and a constant
and a constant ![]() such that
such that
1) ST = TS
2) {P, S} and {Q, T} are asymptotically commuting pairs
3) ![]()
4) ![]()
for all![]() , t > 0 and
, t > 0 and ![]() then P, Q, S, T have a unique common fixed point.
then P, Q, S, T have a unique common fixed point.
3. Main Results
Theorem 3.1: Let ![]() be a complete fuzzy metric space &
be a complete fuzzy metric space & ![]() be any of the continuous t-norms given in 2.1(α) and let A, B, S, T be self maps of X satisfying
be any of the continuous t-norms given in 2.1(α) and let A, B, S, T be self maps of X satisfying
・ The pair {A, S} is reciprocally continuous
・ The pair {B, T} is z-asymptotically commuting
・ The pairs {B, S} and {T, S} commute with each other
・ ![]() (1)
(1)
where![]() ,
, ![]() , then A, B, S, T have a unique common fixed point in X.
, then A, B, S, T have a unique common fixed point in X.
Proof: {A, S} is reciprocally continuous:
⇒ ![]() and
and ![]()
whenever ![]() is a sequence in X such that
is a sequence in X such that
![]() and
and ![]() for some
for some ![]() (2)
(2)
{B, T} is z-asymptotically commuting:
⇒ ![]()
whenever ![]() is a sequence in X such that
is a sequence in X such that
![]() for some
for some ![]() (3)
(3)
・ To prove that![]() :
:
Put ![]() and
and ![]() in (1), we get
in (1), we get
![]()
Letting![]() , we have
, we have
![]() (Since from (2) and (3))
(Since from (2) and (3))
![]() (Since
(Since![]() )
)
![]()
![]()
![]() (from lemma 2.8) (4)
(from lemma 2.8) (4)
i.e., we can find a ![]() such that (2) and (3) holds simultaneously.
such that (2) and (3) holds simultaneously.
Consider (3)
![]()
![]() (Since from (3))
(Since from (3))
![]() (since
(since![]() ) (5)
) (5)
・ To prove that![]() :
:
Put ![]() and
and ![]() in (1), we get
in (1), we get
![]()
![]()
(Since the pairs {B, S} and {S, T} commute with each other).
Taking ![]() on both sides, we have
on both sides, we have
![]()
![]()
![]()
![]() (from lemma (2.8))
(from lemma (2.8))
But from (4), we get ![]() (6)
(6)
・ To prove![]() :
:
Put ![]() and
and ![]() in (1)
in (1)
![]()
Taking limit ![]() on both sides, we get
on both sides, we get
![]() (Since from (2))
(Since from (2))
![]() (Since from (5))
(Since from (5))
![]()
![]()
![]()
![]() (from lemma (2.8))
(from lemma (2.8))
But from (4), we get ![]() (7)
(7)
![]() From (5), (6) and (7) we have
From (5), (6) and (7) we have ![]() (8)
(8)
・ To prove![]() :
:
Consider
![]()
![]()
![]()
![]()
![]()
![]()
![]() (9)
(9)
⇒ from (8) and (9), we have ![]()
![]() z is a common fixed point of A, B, S, T.
z is a common fixed point of A, B, S, T.
・ To prove Uniqueness of z:
Let us assume that A, B, S, T have another common fixed point in X say p where ![]()
i.e., ![]()
Now we prove that![]() .
.
Consider
![]()
![]()
![]() (using lemma (2.8))
(using lemma (2.8))
![]() There exists a unique common fixed point of A, B, S, T in X. W
There exists a unique common fixed point of A, B, S, T in X. W
Example 3.2: Let X = [0, 2], ![]()
![]() where
where ![]() and
and ![]() be the continuous t-norm given by
be the continuous t-norm given by![]() .
.
Clearly, ![]() is a Complete fuzzy metric space.
is a Complete fuzzy metric space.
Let A = 1, ![]() , S = x,
, S = x, ![]() be self maps on X.
be self maps on X.
Let ![]() be a sequence in X.
be a sequence in X.
![]() and
and ![]()
![]() and
and ![]() where
where![]() .
.
⇒ A and S are reciprocally continuous.
Let ![]() be a sequence in X.
be a sequence in X.
![]() and
and ![]() where
where![]() .
.
⇒ B and T are z-asymptotically commuting where z = 1.
Also, the four maps satisfies (iii) and (iv) of theorem 3.1.
⇒ A, B, S, T have a Unique common fixed point in X i.e., at x = 1. W