Received 18 January 2016; accepted 22 March 2016; published 25 March 2016

1. Introduction
A large number of works, in particular [1] - [5] , have been dedicated to the queuing systems (QS) with losses. Building of QS models and determining their characteristics are simplified, if it is assumed that the incoming flow of requests or their service times are exponentially distributed. The rejection of this assumption leads to a considerable complication of the models. In this paper, the model of two-line QS with losses was built on the assumption that the incoming flow of requests and their service times have distributions of general form. For building QS model and determining its stationary characteristics, the theory of semi-Markov processes with arbitrary phase state space [5] - [10] was used.
2. System Description and Building of the Semi-Markov Model
Two-line QS with losses GI/G/2/0 is being considered. It is assumed that the system receives requests, and the time between their arrival is a random variable (RV) 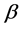 with the distribution function (DF)
with the distribution function (DF) . A received request, with equal probability, starts to be served by one of the available servers or gets lost, if no servers are available. The service time of request by the
. A received request, with equal probability, starts to be served by one of the available servers or gets lost, if no servers are available. The service time of request by the  server-RV
server-RV 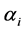 with DF
with DF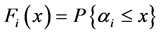 ,
,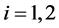 . It is assumed that RV
. It is assumed that RV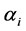 ,
,  are independent, and have densities
are independent, and have densities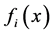 ,
, 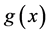 , finite mathematical expectations and variances.
, finite mathematical expectations and variances.
To describe the QS operation, the semi-Markov process [5] - [7] 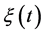 with the following set of states is used:
with the following set of states is used:
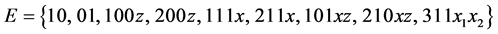 .
.
The meaning of state codes is the following:
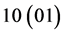 : first (second) server started serving the received request, and second (first) server is available;
: first (second) server started serving the received request, and second (first) server is available;
 : first (second) server became available; second (first) server is available;
: first (second) server became available; second (first) server is available; 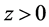 is the time until the arrival of the next request;
is the time until the arrival of the next request;
![]() : first (second) server started serving the received request;
: first (second) server started serving the received request; ![]() is the time until the end of the request service by second (first) server;
is the time until the end of the request service by second (first) server;
![]() : first (second) server became available;
: first (second) server became available; ![]() is the time until the end of the request service by second (first) server;
is the time until the end of the request service by second (first) server; ![]() is the time until the arrival of the next request;
is the time until the arrival of the next request;
![]() : the received request was lost; the times until the end of the request service by first (second) servers are respectively equal
: the received request was lost; the times until the end of the request service by first (second) servers are respectively equal![]() .
.
The time diagram of the system is shown in Figure 1.
Let us define the sojourn times in states of the system. For instance, the sojourn time![]() , in the state
, in the state ![]() is determined by three factors: the time x left until the end of request service by the first server, the time
is determined by three factors: the time x left until the end of request service by the first server, the time ![]() of request service by the second server, and the time
of request service by the second server, and the time ![]() between the request arrivals.
between the request arrivals.
Therefore, ![]() , where
, where ![]() is the minimum sign. Similarly, the sojourn times in other states are determined as follows:
is the minimum sign. Similarly, the sojourn times in other states are determined as follows:
![]() (1)
(1)
We define the transition probabilities of the embedded Markov chain (EMC) ![]() for states
for states ![]() , in the context of other states, they are determined similarly.
, in the context of other states, they are determined similarly.
![]() (2)
(2)
![]()
Figure 1. The time diagram of the system functioning.
3. Definition of the Stationary Distribution of the Embedded Markov Chain
We will find the stationary distribution of EMC![]() . Let us denote
. Let us denote ![]() the values of stationary distribution in states
the values of stationary distribution in states ![]() and assume the existence of stationary densities
and assume the existence of stationary densities ![]()
![]()
![]()
![]() .
.
Introduce the notations:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,![]() .
.
Using (2), set up a system of integral equations to determine the stationary distribution:
![]() (3)
(3)
The last equation in the system (3) is the normalization requirement.
Next, for the sake of simplicity, a homogenous case is considered, and a inhomogeneous case leads to lengthy transformations and results. Let![]() . Then, due to the symmetry of states, we get that
. Then, due to the symmetry of states, we get that![]() ,
, ![]() ,
,![]() .
.
The system (3) is reduced to the following system of equations:
![]() (4)
(4)
Let us introduce the following functions, which are used to record the stationary distribution of EMC:
![]() ―is the density of the renewal function [11]
―is the density of the renewal function [11] ![]() of the renewal process generated by RV
of the renewal process generated by RV![]() ;
;
![]() ―is the density of the direct residual time distribution [11] for the renewal process generated by RV
―is the density of the direct residual time distribution [11] for the renewal process generated by RV![]() ;
;
![]()
![]() ―is the density of the renewal function, renewal process generated by RV with the distribution density
―is the density of the renewal function, renewal process generated by RV with the distribution density![]() ;
;
![]() (5)
(5)
Using the method of successive approximations [12] , we can show that the system (4) has the following solution:
![]() (6)
(6)
The constant ![]() is found by means of normalization requirement; its explicit form is not used when finding the QS stationary characteristics.
is found by means of normalization requirement; its explicit form is not used when finding the QS stationary characteristics.
The system of equations, which is almost identical to the system (3), and its solution method are covered in [13] .
4. Definition of Stationary Characteristics of System
Let us turn to the determination of the stationary characteristics of the QS. Using Formulas (1), we will define the average sojourn times in states of the system:
![]() (7)
(7)
We divide the set of states E into three following subsets:
![]() ―all servers are available;
―all servers are available;
![]() ―one server is in service;
―one server is in service;
![]() ―two servers are in service;
―two servers are in service;
![]() ,
,![]() .
.
We will introduce the transition probabilities of the semi-Markov processes![]() :
:
![]() ,
,
and
![]() ―stationary probabilities,
―stationary probabilities,![]() .
.
We will show that the stationary probabilities of QS ![]() are defined by the following formulas:
are defined by the following formulas:
![]() (8)
(8)
where
![]() (9)
(9)
![]() ―is the renewal function [11] ;
―is the renewal function [11] ;
![]() ―is DF of the direct residual time [11] ;
―is DF of the direct residual time [11] ; ![]()
![]() ―is the mathematical expectation of the direct residual time [11] .
―is the mathematical expectation of the direct residual time [11] .
The proof. As is known [5] [6] , the following equalities are true:
![]() (10)
(10)
where![]() ―is the average sojourn time of SMP
―is the average sojourn time of SMP ![]() in state
in state![]() ;
;
![]() ―is the stationary distribution of EMC
―is the stationary distribution of EMC![]() .
.
Let us calculate the integrals entering into the right side of equalities (10). Using (6), (7), we get:
![]()
In the transformations, the following formula was used:
![]() .
.
![]()
![]() (11)
(11)
![]() (12)
(12)
By substituting the determined expressions in Formulas (10), we get Formulas (8).
Let us define the stationary probability of request loss. We will consider the subset of states:
![]() ―a received request was lost.
―a received request was lost.
We will find ![]()
![]()
Therefore, the stationary probability of request loss equals:
![]() (13)
(13)
Important characteristics of the QS under consideration are average stationary sojourn times ![]() of the system in the selected subsets of states
of the system in the selected subsets of states![]() . To determine them we will use Formulas [5] [6] :
. To determine them we will use Formulas [5] [6] :
![]() (14)
(14)
Let us find the values of the expressions in the denominators of Formulas (14).
![]() (15)
(15)
The transformations used the following formula:
![]() , (16)
, (16)
which results from the first equation of the system (4),
![]() (17)
(17)
![]() (18)
(18)
In the derivations of equalities (17), (18) Formula (16) was used in the same way.
Having placed the determined values of the denominators into Formulas (14), we obtain:
![]() (19)
(19)
![]() ,
,
![]() .
.
5. Particular Cases of QS GI/G/2/0
Let us look at particular cases of QS GI/G/2/0.
1) We find the stationary characteristics of QS![]() . In this case,
. In this case,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
,
![]()
![]()
![]()
![]()
Using Formulas (8), (13), (19), we obtain:
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
2) Let us examine QS M/G/2/0, ![]() ,
,![]() .
.
The direct substitution into the system (4) can show that the stationary distribution of EMC is determined by the formulas:
![]()
Functions (5) in this case are as follows:
![]()
![]() ―is the density of function 1: of renewals [11] ;
―is the density of function 1: of renewals [11] ;
![]() ―is the density of function 0: of renewals [11] ;
―is the density of function 0: of renewals [11] ;
![]()
Consequently,
![]() .
.
Using Formulas (8), (13), (19), we obtain that the stationary characteristics of QS M/G/2/0 are written as:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Thus, in this case, as shown in [4] , stationary probabilities ![]() are invariant under the laws of distribution of service time.
are invariant under the laws of distribution of service time.
The semi-Markov model of QS ![]() is considered in [14] .
is considered in [14] .
In the paper [5] , a similar approach to the building of QS model under consideration is used. To find the stationary distribution of EMC, a method based on the usage of taboo-probabilities is applied.
In monograph [13] , the semi-Markov model of QS ![]() is considered and stationary characteristics are defined.
is considered and stationary characteristics are defined.
Using built semi-Markov model, limiting theorems and Markov renewal equations [5] - [7] , one can find other stationary and non-stationary characteristics of QS![]() .
.