Global Existence of Periodic Solutions in a Nonlinear Delay-Coupling Chaos System ()

Abstract

Keywords

Share and Cite:

Received 29 January 2016; accepted 18 March 2016; published 21 March 2016

1. Introduction

In the 19th century, H. Poincaré found that three-body gravitational interactions can produce amazing complex behaviors by studying the celestial mechanics, that is, there may be uncertainty even in the dynamic equations of very simple object interactions. He found that some systems have sensitive dependence on initial values and behavioral unpredictability. It is the first discovery of chaos. In 1963, E.N. Lorenz [1] unexpectedly discovered the first chaotic attractor in simulating weather, since then, chaos occurs in many areas and has access to the far- reaching development.

Since the discovery of chaos, it has been highly regarded in many areas, such as mathematics, mechanics, meteorology, astronomy, and economics. Chaos can be used to achieve the encrypted transmission of infor- mation. If the information is hidden in the chaotic signal, when the receiver has synchronized with the trans- mitter signal, the signal can be obtained, rather than by other people. The important feature of chaos is its highly sensitive to initial values, which makes it difficult to control. In practical applications, we hope to eliminate the negative effects resulting chaos and strengthen its positive effects. This makes the chaos control has become a highly anticipated new field. In particular, we can control the bifurcation of system [2] , such as retarding the occurrence of inherent bifurcation, stabling bifurcation solution, changing the shape or type of bifurcation, and controlling multiplicity of the limit cycle, amplitude or frequency. It has formed a number of chaos control methods, such as the OGY method [3] , variational parameter control [4] , state feedback control [5] , adaptive control [6] , optimal control [7] , robust control [8] and non-feedback control [9] . As an important research aspect of chaos control, chaos synchronization has also been widely concerned, resulting in a variety of effective methods: PC synchronization [10] , active-passive synchronization [11] , chaos synchronization based on mutual coupling [12] and adaptive synchronization method [13] . Chaos control and chaos synchronization are identical. These methods often make the dimension of original system increases, forming a new coupled system. In order to understand the ultimate effect of chaos control and synchronization, we not only need to know the dynamic behavior of original system, but also need to discuss the one of new coupled system (see [14] - [18] ).

A system with unidirectional nonlinear delayed-coupling scheme is considered in this paper. T. Banerjee et al. [19] proposed system

(1)

where x is the state variable, 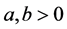are system parameters, and 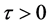is the time delay. f is the nonlinear function. When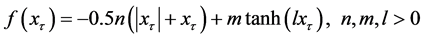, [19] has reported that as b or 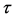varies, chaos and hyperchaos are observed. Furthermore, [20] studied the synchronization of the following coupled system.

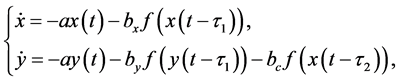(2)

where x and y are drive and response variables. 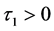is the system delay, and 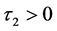is the coupling delay. and are as usual positive parameters. The value of determines the strength of the coupling. Our purpose is to investigate the global existence of periodic solutions for the system.

The remainder of this paper is organized as follows. In Section 2, we employ the preliminary results about the existence of the local Hopf bifurcation. In Section 3, the global Hopf bifurcation is established. An example is given in order to illustrate the results obtained in Section 4.

2. Preliminary Results

We present some preliminary results of system (2) about the existence of local periodic solutions. This is the basis of the global Hopf bifurcation.

Let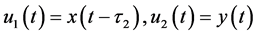, and denote as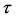. Using x and y to represent the variables still, Equation (2) can be written into the following system

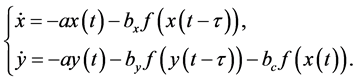(3)

Clearly, is an equilibrium point. The characteristic equation of its corresponding linear system around is

(4)

that is,

(5)

or

(6)

When, the eigenvalues are.

Let be a pair of roots of Equation (5). Substitute into Equation (5) and separate the real and imaginary parts

(7)

Denote (H₁) and (H₂). Let be a root of Equa- tion (4) near satisfying.

Lemma 1. If (H₁) or (H₂) is satisfied, then

Lemma 2. 1) If (H₁) and (H₂) are not satisfied, then all roots of Equation (4) have negative real parts for any.

2) If (H₁) is satisfied, then there exists a sequence of satisfying such that Equation (4) has a pair of purely imaginary roots when, and all roots of Equation (4) have negative real parts when.

3) If (H₂) is satisfied, then there exists a sequence of satisfying such that Equation (4) has a pair of purely imaginary roots when, and all roots of Equation (4) have negative real parts when.

4) If (H₁) and (H₂) are satisfied, then there exists a sequence of satisfying and such that Equation (4) has two pairs of purely imaginary roots when, and all roots of Equation (4) have negative real parts when, where

and

Using the lemmas above, we have Theorem 1.

Theorem 1. Suppose (H₁) is satisfied.

1) If (H₁) and (H₂) are not satisfied, then the zero equilibrium point of system (3) is asymptotically stable for any.

2) If (H₁) is satisfied, then the zero equilibrium point of system (3) is asymptotically stable when and unstable when. System (3) undergoes a Hopf bifurcation at when.

3) If (H₂) is satisfied, then the zero equilibrium point of system (3) is asymptotically stable when and unstable when. System (3) undergoes a Hopf bifurcation when.

4) If (H₁) and (H₂) are satisfied, then the zero equilibrium point of system (3) is asymptotically stable when

and unstable when. System (3) undergoes a Hopf

bifurcation when, where are defined above.

3. Global Existence of Periodic Solutions

In this section, we study the global continuation of periodic solutions bifurcating from the point, , ,. Throughout this section, we follow closely the notations in Wu [21] and let (H₁) or (H₂) be satisfied, namely local Hopf bifurcation occurs. We define

and let denote the connected component of in, where and

are defined in Lemma 2.

We assume (H₁) or (H₂) is satisfied so that the local Hopf bifurcation occurs.

Lemma 3. If is bounded, then all periodic solutions of the system (3) are uniformly bounded.

Proof. Suppose that there exists such that, is a nonconstant peri- odic solution of system (3) and have maximums at, respectively, then. We have

This shows that the periodic solutions of (3) are uniformly bounded.

Lemma 4. System (3) has no nontrivial t-periodic solution.

Proof. If system (3) has a nontrivial t-periodic solution, then

(8)

has a nontrivial periodic solution.

However, system (8) only has trivial periodic solutions. In fact,

only has a trivial periodic solution (i.e., equilibrium). Moreover,

has no nontrivial periodic solution.

Thus, system (3) has no nontrivial t-periodic solution.

Next, we show system (3) has no nontrivial 2t-periodic solution.

Lemma 5. Assume

(H₃)

is satisfied, system (3) has no nontrivial 4t-periodic solution. Moreover, system (3) has no nontrivial 2t-periodic solution.

Proof. Let be a 4t-periodic solution of system (3).

Then is a periodic solution to the following system of ODE:

(9)

where and,.

From Lemma 3, the periodic orbit of the system (9) belongs to the region:

(10)

If we want to prove there is no nontrivial 4t-periodic solution in (3), it suffices to prove that there is no nonconstant periodic solution for (9). To do this, we apply the general Bendixson’s criterion in higher dimensions developed by Li & Muldowney [22] . It is easy to compute the Jacobian matrix of the system (9) for:

Then the second additive compound matrix of is a matrix defined as follows.

For any integers, the element in the i-row and the j-column of is

Choose a vector form in as

With respect to this norm, we can obtain that the measure of the matrix is given by

(11)

By Corollary 3.5 of Li & Muldowney [22] , the system (9) has no periodic orbit in G if. By

(11), we have if and only if

(12)

So we get (9) only has trivial periodic solutions when (H₂) is satisfied.

Thus, (9) has no nontrivial periodic solution. System (3) has no 4t-periodic solution.

Theorem 2. Suppose that (H₁)/(H₂) and (H₃) are satisfied, then, for each, system (3) has

nonconstant periodic solutions with periods in, respectively. Here,

are defined in Lemma 2.

Proof. We can prove that the projection of onto t-space includes,. We have given the characteristic matrix of the system (3) at zero equilibrium.

By Lemmas 1 and 2, there exist, and a smooth curve such that and

Then.

Denote and

Obviously, if and such that, then, ,. Set

We obtain the crossing number

We conclude that

By Theorem 3.3 of Wu [21] , is unbounded.

Lemma 3 implies that the projection of onto the z-space is bounded.

From the definition of, we know that

Hence

From Lemmas 4 and 5, we know that if, andif. So, to make unbo- unded, the projection of onto t-space must be unbounded. Obviously, are pairwise disjoint. So system (3) has nonconstant periodic solutions for.

In this section, we derive the global existences, number and periods of periodic solutions. However, the stability of periodic solutions far away from is unclear.

4. An Example

Choosing and with , system (2) can be expressed as follows:

(13)

[19] gave the curves of corresponding to different parameters and l (see Figure 1). It evidences is bounded when (A is any finite constant).

For system (13), , and. (H₁) is satisfied and (H₂) isn’t. Furthermore,.

System (13) has a periodic solution near. As shown in Figure 2 at.

(H₃) is correct, and we now show large amplitude periodic solutions exist for values of far away from. This indicates the global existence of periodic solutions. As shown in Figure 3 at.

5. Conclusion

In our paper, the effect of parameters on dynamics of a unidirectional nonlinear delayed-coupling chaos system at the zero fixed point is investigated. There exist the critical values of Hopf bifurcation and small amplitude periodic solutions. Furthermore, we derive that the local periodic solutions also exist globally for. In addition, the results indicate the variation of dynamics of system (2) is owing to the inherent delay, and not owing to the coupled one. Our results are propitious to investigate chaos synchronization using system (2), especially synchronization of periodic solutions. However, it still needs to study further for the dynamics of bidirectional coupled system.

Acknowledgements

We thank the Editor and the referee for their comments. The research is supported by National Natural Science Foundation of China (No. 11301263), the Jiangsu Natural Science Foundation (No. BK20140927), the Ningxia Natural Science Foundation (No. NZ13213) and the Ningxia Higher Educational Science Program (No. GX2014[222]17).

Conflicts of Interest

The authors declare no conflicts of interest.

References