Neural Network for Estimating Daily Global Solar Radiation Using Temperature, Humidity and Pressure as Unique Climatic Input Variables ()
Received 21 November 2016; accepted 15 March 2016; published 18 March 2016
1. Introduction
Solar radiation is an important parameter for research related to solar energy. The solar energy importance is that it can play a key role in the decarbonisation of the global economy along with improvements in energy efficiency and imposing costs on greenhouse gases emissions [1] . Furthermore, solar radiation is widely used for the applications development, such as photovoltaic systems, that convert solar energy directly into electrical energy without harming the environment, and development of crop growth models based mainly on processes photosynthetic [2] .
Unlike other climate variables such as ambient temperature and relative humidity, the solar radiation is barely measured [3] . Even if there exist some weather stations nearby, access to data is often limited. Also, it is common for weather data to have many missing values (from a few minutes to several days missing measurements), or they are out of range due to equipment malfunction [4] [5] . So, in those cases it is possible to obtain reasonably accurate estimates of their value using computational models.
In the literature, we can find a wide variety of methods to estimate solar radiation. There are empirical models [3] [6] [7] , statistical approaches [8] [9] , others based on linear regression [10] - [13] and nonlinear [11] [14] and based on artificial intelligence techniques. In the latter group, the use of artificial neural networks is the most extended [10] [15] , although some authors have proposed methods that use techniques such as Fuzzy Logic [11] and Particle Swarm Optimization [16] , among others [11] [17] . A complete review of these methods can be found in [1] [18] [19] .
Many of these methods include empirical relationships between solar radiation and astronomical factors (Earth-sun distance, solar declination, hour angle, etc.), geographic factors (latitude, longitude and elevation of the site), physical factors (diffusion of air molecules, water vapor content, the spread of dust, etc.) and weather factors (sunshine, temperature, rainfall, relative humidity, cloud cover, etc.) [1] . The empirical models based on meteorological factors that provide more accurate estimates use mainly sunshine hours and cloudiness as input variables [20] , but other variables such as precipitation, relative humidity, temperature point spray, among others, are also very common. Therefore, a proper method for a particular purpose and a particular location should take into account data availability and expected accuracy. In the particular, case where measurements of cloudiness and sunshine hours are not available, there are other models, based on different sets of variables available on the most weather stations, such as ambient temperature, relative humidity and atmospheric pressure.
The aim of this paper is to propose a method for estimating daily global solar radiation, based on an empirical model and neural network. The proposed method uses the empirical model to generate initial estimates, which are then used along with temperature, relative humidity and atmospheric pressure as input variables for the neural network to improve estimates. As part of this study, we make a comparison of different mathematical methods to determine which one provides better initial estimates of solar radiation. Both empirical models and neural network are adjusted and validated using weather data from automated weather stations located in the province of Tucumán, Argentina. Finally, the proposed method is compared with linear regression to determine if the relationship between input data and output data has indeed nonlinear components.
The rest of this paper is organized as follows: Section 2 describes the materials and methodology used for estimating daily global solar radiation; Section 3 details the results for both the empirical model and the method based on neural networks; finally in Section 4 the conclusions are presented.
2. Materials and Methodology
2.1. Data Description
The weather data used in this work were collected from five weather stations belonging to Estación Experimental Agroindustrial Obispo Colombres (E.E.A.O.C.), located in the province of Tucumán, Argentina. The dataset corresponds to average values of samples taken every 15 minutes, in the period between 01-01-2010 and 20- 11-2013. Among all the variables provided by the weather stations, in this paper we use:
・ Temperature [˚C]
・ Relative Humidity [%]
・ Atmospheric Pressure [hPa]
・ Observed Solar Radiation [W/m2]
In the initial analysis of the dataset, and as usually happens in distributed sensor networks, there are records with missing or erroneous values (out of range), varying from a few days to a few weeks. This is usually caused by problems in measuring devices or data transmission and storage or poorly calibrated instrumentation [21] . Because the amount of missing data is not significant, we decided to remove the complete records that present any anomaly. Also, the data were not filled to prevent the filling procedure introduce deviations that can affect the results. Table 1 shows a summary of missing values for each weather station and a statistical description of the dataset.
From the database described above, a new database is generated with daily values, which was used in the tests in this paper. This new database is composed of maximum, minimum and average temperature, average relative humidity, average atmospheric pressure and global solar radiation [MJ/m2].
2.2. Initial Model for Estimating Global Solar Radiation
A large percentage of empirical methods found in the literature use empirical relations to estimate the global solar radiation from climatic variables. Many of them include extraterrestrial radiation (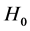
), which is calculated using standard geometric properties. The process described below is based on [6] :
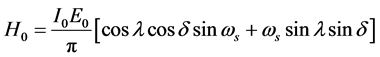(1)
where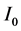 
is the solar constant, equal to 118.11 [MJ/(m2∙day)]; 
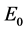is a correction factor for the eccentricity of the orbit of the Earth, 
is the longitude of the location,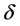 
is the solar declination and 
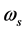is the hour angle of the sun.
The factor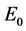 
is defined as the square of the ratio between current Earth-Sun distance (R) and the average
![]()
Table 1. Statistical description of the climate database.
Earth-Sun distance (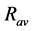
), which is calculated as:
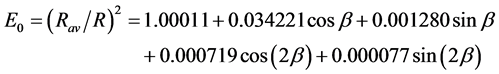(2)
where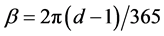 
is the day of the year (d) in radians.
The solar declination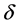 
is the angle between the rays of the sun and the plane of the Earth equator. It is obtained by the following equation:
(3)
where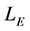 
is the ecliptic longitude which indicates the position of the Earth in its orbit. Since the eccentricity of the orbit of the Earth is small, we can consider that is circular, committing an error of about 1 degree. So, the solar declination is calculated using the following expression:
![]()
(4)
The hour angle of the sun ![]()
is defined as its angular displacement, taking positive values before noon and negative values in after noon. The hour angle of the sun can be calculated using the following equation:
![]()
(5)
To choose a method for the initial estimates of global solar radiation, different models based only on temperature were tested. To adjust the empirical parameters of these models, a local search algorithm was implemented, Hill Climbing [22] . This algorithm was used because some of the models are nonlinear respect to the parameters, preventing the use of deterministic methods, such as regression analysis. Thereby, using data from the meteorological station located in El Colmenar, we seek the optimal combination of parameters, so as to minimize the error committed by the model. Table 2 shows the errors obtained in each case. We can see that the models proposed by [23] and [24] are those that achieved best results in terms of accuracy. However, in this paper we use the Annadale’s model because it is simpler and requires less parameter adjustment. Then, the daily global solar radiation is calculated using the following equation:
![]()
(6)
where ![]()
and ![]()
are empirical coefficients adjusted with historical data of temperature and global solar radiation, and Z is the altitude of the location (450 meters in Tucumán). A complete description of the tested models and their corresponding mathematical formulas can be found in [6] .
2.3. Feedforward-Backpropagation Neural Network
![]()
Table 2. Error values obtained with empirical models, using the data from El Colmenar.
weights, which are adjusted iteratively by a training algorithm. For each iteration (or step), the algorithm compares the output and target values, so as to minimize the error. The training process ends when the network is capable of reproducing the outputs corresponding to the input parameters.
Multilayer Feedforward is a kind of neural network, which consist of a number of layers: the first has neurons directly connected to the input data, and they are linked to one or more neurons in a hidden layer, or directly connected to the neurons in the output layer. In this kind of network, all neurons in one layer are full connected to all neurons of the next layer, and there are no feedbacks or recurrent connections.
In this work, we decided to use a Multilayer Feedforward Neural Network with 4 neurons in a single hidden layer, as show in Figure 1. Hyperbolic tangent sigmoid transfer function is used in the hidden layer and linear transfer function for neurons in the output layer. The neural network was trained with the Levenberg-Marquardt Backpropagation algorithm [25] , due to its high efficiency and fast convergence, although their computational requirements are high [26] . For the purpose of developing, testing and validating the ANN-model, the data from the meteorological station located in El Colmenar was divided into two subsets following a uniformly random distribution [27] , taking 80% as training set and 20% as testing set. The stop criterion consists of at most 50 iterations or until it is verified that the error in the testing set is higher than in the training set for 10 consecutive epochs.
The input vector of the neural network consists of global solar radiation estimates (H) calculated with Equation (6), the solar zenith angle (![]()
) in radians calculated with Equation (7) and climatic variables (mean relative humidity and maximum, minimum and average temperature) described in Section 2.1.
![]()
Figure 1. Architecture of a multilayer feedforward neural network.
![]()
(7)
Additionally, in order to improve the accuracy of estimates, information from the previous day is included as new independent variables called lagged variables [28] . Thus, the number of input variables of the system is duplicated (12 variables in total). In preliminary tests it was determined that considering variables corresponding to 2 or more days before does not generate a significant improvement.
2.4. Lineal Regression
In other works [10] [13] [29] , linear regression was used to estimate solar radiation in different locations in Argentina, obtaining good results. This shows that solar radiation has a linear relation with other weather variables, mainly temperature, humidity, sunshine hours and cloudiness, among others. However, when these variables are not available, the quality of the estimates obtained with linear regression can be reduced. Then, to verify the presence of non-linear components in the problem, we also use linear regression to estimate the values of solar radiation, and then compare the values obtained with those obtained with neural networks. The input variables used in both cases are the same.
The inclusion of past information as lagged variables in the input vector generates a strong correlation between some of the input variables. For this reason, the linear systems involved can be ill-conditioned (produce a strong variation in the output for small changes in the input) [30] [31] , making the solution not adequate. To avoid this problem we use Moore-Penrose pseudoinverse [30] , which is able to obtain good solutions even in the presence of ill-conditioned systems.
2.5. Statistical Analysis
In order to evaluate the performance of the implemented models, the errors obtained are analyzed using different metrics commonly used in the literature, comparing the calculated solar radiation values (![]()
) with solar radiation measurement (![]()
). The error metrics used are: Root Mean Squared Error or RMSE (Equation (8)), whose value is interpreted easily because it is expressed in the same unit that the variable to be estimated; Percentage Root Mean Squared Error or RMSE% (Equation (9)), which expresses the RMSE as percentage; Mean Bias Error or MBE (Equation (10)), which allowed us to know if there is an underestimation or overestimation, analyzing its sign; Pearson’s Correlation Coefficient R (Equation (11)), which helps to determine the extent that the model follow the general trend of the data.
![]()
(8)
![]()
(9)
![]()
(10)
![]()
(11)
3. Results and Discussion
The errors obtained using the simple empirical model, using linear regression and using a neural network are shown in Table 3. It is clear that neural networks generate results with lower errors in all cases. Considering RMSE values, the error reduction of neural network compared to empirical model is 30.9% in El Colmenar, 32.0% in Santa Ana, 28.0% in Pueblo Viejo, 29.3% in Monte Redondo and 23.4% in Casas Viejas. Note that error levels obtained from dataset from El Colmenar are lower in all three cases. This occurs because data from El
![]()
Table 3. Statistical results for the basic empirical, linear regression and neural networks models.
aValues used for training or parameter adjustment.
Colmenar were used to adjust the empirical model, obtain the linear regression coefficients and train the neural network. Furthermore, comparing the results obtained, you can see that the error reduction when using neural networks regarding linear regression is 6.6% for training set (data from El Colmenar) and 10.0% on average for the validation cases. These differences show that the relationship between solar radiation and the input variables present nonlinear components.
The use of lagged variables allows improving the estimates accuracy. According to preliminary tests, which are not detailed in this work, use these additional variables allows a reduction between 10% and 15% in the estimates obtained with neural networks. Since the total amount of variables is not excessive (in total 12 input variables were used), it was not necessary to implement a method for selecting variables.
The use of lagged variables allows improving the estimates accuracy. According to preliminary tests, which are not detailed in this work, use these additional variables allows a reduction between 10% and 15% in the estimates obtained with neural networks. Since the total amount of variables is not excessive (in total 12 input variables were used), it was not necessary to implement a method for selecting variables.
Figure 2 and Figure 3 show the scatter plots of measured and estimated solar radiation data, from El Colmenar (training) and Casas Viejas (validation). It is evident that there is a slight underestimation for values greater than 25 [MJ/m2], and a slight overestimation for values less than 5 [MJ/m2]. This model behavior occurs for both the training set and the validation set. However, in general the trained model achieves correctly grasp the trend of the data, and this is reflected in the R values near 1 in Table 3. The scatter plots for the rest of the weather stations were similar to those shown from Casas Viejas. Finally, in Figure 4 you can see and compare curve profiles of real and estimated solar radiation data.
4. Conclusions
This paper presented a methodology for estimating solar radiation based on empirical models and artificial neural networks, using temperature, relative humidity and atmospheric pressure as unique climatic input variables. From the results obtained, we present the following conclusions:
・ The proposed methodology is used to estimate the daily global solar radiation satisfactorily, even without some of the variables considered critical that the literature reports as necessary for a good estimate.
・ Using the neural network significantly improves the accuracy over estimates obtained only using the empirical model.
![]()
Figure 2. Results obtained with neural networks on data from (a) El Colmenar (training set) (b) Casas Viejas (validation set).
![]()
Figure 3. Results obtained with neural networks on data from Casas Viejas (validation set).
![]()
(a)![]()
(b)
Figure 4. Daily Global Solar Radiation estimates obtained using neural networks. (a) El Colmenar (training set). (b) Casas Viejas (validation set).
・ By using lagged variables is possible to improve the result. Considering more time backwards the number of variables increases, but in some cases this allows to increase the accuracy of the estimates. However, the use of too many variables may increases the complexity of the problem, so it is recommended the use of some variable selection method to avoid these problems.
・ The error obtained is slightly higher than the error obtained in other works that estimate solar radiation in Tucumán [13] . This result is expected since in our case the input variables are restricted to only three (temperature, humidity and pressure).
In this work, a single empirical model is included as input to the neural network. However, the methodology used allows us to include more than one.
Acknowledgements
This work was partially supported by grants PID-UTN 25/P051 UTI 1757. We also wish to extend thanks to Estación Experimental Agroindustrial Obispo Colombres to provide the data necessary to make this paper.