Pressure Characteristics Study for the Configuration of Sudden Expansion with Central Restriction and Suction ()
Received 20 November 2015; accepted 14 March 2016; published 17 March 2016

1. Introduction
In plain sudden expansion configuration, the fluid is required to flow through a passage of sudden increasing cross-sectional area; this results in a recovery of static pressure. Because, significant amount of energy is transferred from the main flow irreversibly to the recirculating eddies. However, since the flow is subjected to adverse pressure gradient, the flow separates from the walls resulting in substantial loss of stagnation pressure. As stagnation pressure is a matter of utmost significance in assessing the performance of various components and the cycle of a gas turbine based power plant, such losses in stagnation pressure in sudden expansion geometry may drop the overall plant efficiency. In this paper, study on pressure characteristics of fluid passing through sudden expansion configuration has been carried out by incorporating central restriction in the inlet zone and suction at the top corner on side wall. The most remarkable feature of this study is that it clearly shows the advantages of sudden expansion with central restriction and suction over the plain sudden expansion configuration or sudden expansion with central restriction only as far as the maximum magnitude of the static pressure rise is concerned.
From a brief review of literature, it appears that the first work in the field of plain sudden expansion configuration has been carried out by Macagno and Hung [1] . They have carried out computational and experimental study on the flow of a viscous liquid through axisymmetric sudden expansion configuration. They have considered an expansion ratio of 2:1 and for Reynolds number up to 200. They have observed that the vorticity lines are stretched in the direction of the flow when the Reynolds number becomes higher. Kwon et al. [2] have numerically described an economical prediction procedure for fully developed incompressible flow through a symmetric sudden expansion channel. They have considered two-dimensional boundary layer equations for incompressible, steady and laminar flow. They have considered Reynolds numbers (based on channel inlet height) ranging from 1 to 320 for fully developed laminar flow undergoing a sudden 2:1 expansion. Budwig et al. [3] have experimentally investigated the flow characteristics of laminar pulsatile flow through an axisymmetric sudden expansion configuration. In their configuration, a diameter ratio of 2.25 is used by them. For steady flow, they have used the Reynolds number of 131 and 253, based on the bulk velocity and upstream tube diameter. They have concluded that the flow patterns for a strongly pulsating flow in an axisymmetric sudden expansion differ dramatically from steady flow patterns. Mandal and Majumder [4] have numerically investigated the effects of inlet center line turbulence on reattachment length in an axi-symmetric sudden expansion. They have used area ratio of 1.47 for an axial velocity as 10.6 m/s. They have observed that the recirculation bubble and reattachment length decrease with the increase in center line turbulence intensity. But after a certain limit of intensity, reattachment length is constant.
Sheen et al. [5] have experimentally investigated the flow characteristics in a concentric annular flow over an axisymmetric sudden expansion with inlet modification. They have used a centrebody at the inlet region to the sudden expansion configuration and inlet region becomes concentric annulus shape. They have considered Reynolds number ranging from 150 to 5800, based on the volumetric mean axial velocity and hydraulic diameter of the annular pipe. For their configuration, the diameter expansion ratio is considered 1.987. Four typical flow patterns are observed by them. These are open annular flow, closed annular flow, vortex shedding, and stable central flow. Chakrabarti et al. [6] have numerically carried out the performance simulation of a vortex controlled diffuser in low Reynolds number regime. They have considered a sudden expansion configuration with suction slot on different position of vertical and horizontal walls. They have used Reynolds number ranging from 20 to 100, aspect ratio for 2 and 4, and bleed fraction for 2 percent, 5 percent and 10 percent. They have observed that static pressure rise increases with increase in bleed. They have established that the position of the bleed slot should be located preferably at the vertical wall top corner of the vortex controlled diffuser for the best performance. Layek et al. [7] have carried out numerical simulation to study the effects of suction and blowing on flow separation in a symmetric sudden expansion channel. They have considered uniform blowing or suction at the lower and upper porous step walls. They have used expansion ratio of 1:2 and non-dimensional inlet channel length of 4. During computation, Reynolds number ranging from 100 to 500 is considered by them. They have observed that the blowing through the channel wall makes the asymmetric nature of flow to the symmetric by diminishing the region of separation. But the symmetric nature of flow becomes asymmetric by the application of suction from the porous channel wall. Takano et al. [8] have experimentally studied the detailed structure of separated flow downstream of a backward facing step configuration. They have considered a non-uniform periodic disturbance along spanwise direction by using an injection of synthetic jet array. They have used an expansion ratio of 1.67 with a step height of 4 mm. The Reynolds number based on the step height ranged from 300 to 900 is considered. They have observed that non uniform injection velocity affects the distorted vortex structure and reattachment distribution in the span wise direction which strongly depends on the Reynolds number and injection velocities of the synthetic jet array. Tuncer et al. [9] have experimentally investigated the stability and structure of lean premixed methane air flames in a swirl stabilized premixed dump combustor at atmospheric pressure. At the inlet of the dump plane, they have considered a 45˚ angled eight blades swirl vane which is installed on a 20 mm diameter centre body. They have observed two elliptically shaped counter rotating recirculation vortices behind the dump plane and a central recirculation zone just downstream of dump plane. Cerantola and Birk [10] have experimentally and numerically evaluated short annular diffusers with conical expansion at exit of the annulus using swirlers with different swirl angles. They have considered three area ratios such as 1.61, 1.91 and 2.73 for an inlet Reynolds number of 1.4 × 105. For 10 deg inlet swirl, they have observed that AR = 1.91 diffuser gives highest performance. Taamallah et al. [11] have experimentally studied the link between the flame macroscale structure and thermo-acoustic instabilities, in a premixed swirl-stabilized dump combustor. They have concluded that dynamic modes in the long combustor are mostly associated with specific mean flame brush spatial distributions.
As per brief review of literature, it is noted that a number of researchers have studied the flow characteristics of fluid passing through plain sudden expansion configuration. But, the numerical or experimental study on plain sudden expansion configuration with some modifications is very few [5] - [11] . Again, it is noted that systematic detailed study on the pressure characteristics in case of sudden expansion configurations with central restriction and suction is not addressed. Therefore, in this paper an attempt has been made to study the effect of Reynolds number, percentage of central restriction, aspect ratio and percentage of suction on average static pressure distribution and average stagnation pressure distribution for sudden expansion with central restriction and suction configuration.
2. Mathematical Formulation
2.1. Governing Equations
Schematic diagrams of the computational domain for flow through plain sudden expansion, sudden expansion with central restriction only, and sudden expansion with central restriction and suction are illustrated in Figure 1(a)-1(c) respectively. The flow under consideration is assumed to be steady, two-dimensional and laminar. The fluid is considered to be Newtonian and incompressible.
The following dimensionless variables are defined to obtain the governing conservation equations in the non- dimensional form;
Lengths: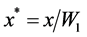 ,
, 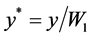 ,
, 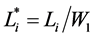 ,
,  ,
, 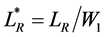 ,
,  ,
, 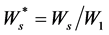 ,
,
Velocities: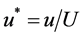 ,
, 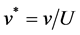 ,
,
Pressure: .
.
With the help of these variables, the non-dimensional mass and momentum conservation equations are written as follows:
 (1)
(1)
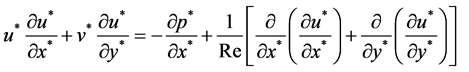 (2)
(2)
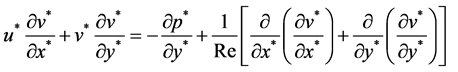 (3)
(3)
where, the flow Reynolds number, .
.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 1. (a) Schematic diagram of the computational domain for the configuration of plain sudden expansion; (b) Schematic diagram of the computational domain for the configuration of sudden expansion with central restriction only; (c) Schematic diagram of the computational domain for the configuration of sudden expansion with central restriction and suction.
2.2. Boundary Conditions
Four different types of boundary conditions are applied to the present problem. They are as follows:
1) At the walls: No slip condition is used, i.e., ![]() ,
,![]() .
.
2) At the inlet: Axial velocity is specified and the transverse velocity is set to zero, i.e., ![]()
![]() . Fully developed flow condition is specified at the inlet, i.e.,
. Fully developed flow condition is specified at the inlet, i.e.,![]() .
.
3) At the exit: Fully developed condition is assumed and hence gradients are set to zero, i.e., ![]() ,
,![]() .
.
4) At the line of symmetry: The normal gradient of the axial velocity and the transverse velocity are set to zero, i.e., ![]() ,
,![]() .
.
2.3. Numerical Procedure
The partial differentials Equations (1), (2) and (3) are discretised by a control volume based finite difference method. Power law scheme is used to discretise the convective terms (Patankar, [12] ). The discretised equations are solved iteratively by SIMPLE algorithm, using line-by-line ADI (Alternating directional implicit) method. The convergence of the iterative scheme is achieved when the normalised residuals for mass and momentum equations summed over the entire calculation domain fall below 10−8.
In the computation, flow is assumed fully developed at the inlet and exit. Therefore, exit is chosen far away from the throat. The distribution of grid nodes is non-uniform and staggered in both coordinate direction allowing higher grid node concentrations in the region close to the step and walls. During computations, the non-di- mensional inlet (![]() ) and the exit (
) and the exit (![]() ) lengths are considered as 1 and 50 respectively for AR = 1.5, 2 and 3. However, the computations are also performed with
) lengths are considered as 1 and 50 respectively for AR = 1.5, 2 and 3. However, the computations are also performed with ![]() = 100. The obtained results are having no significant variation on the important design parameters. The grid sensitivity study has been performed carefully for a typical aspect ratio (AR) of 2 and Re = 100 with 20% central restriction (CR). Several test cases are run by using different grid size to quantify grid independence study in terms of magnitude and location of Ψmax. Finally in our work we have considered the meshes comprising of 41 × 37 grid nodes in the inlet section and 221 × 121 grid nodes in the exit section in the x- and y-directions, respectively. For higher aspect ratio like AR = 4, 5 and 6, the grid sensitivity study has been performed considering typical aspect ratio of 5, Reynolds number of 100% and 20% central restriction. For these aspect ratios, the non-dimensional inlet and the exit lengths are considered as 1 and 200 respectively. The meshes comprising of 41 × 37 grid nodes in the inlet section and 457 × 193 grid for the exit section in the x- and y-directions, respectively are used. This study has been discussed in detail by Das and Chakrabarti [13] .
= 100. The obtained results are having no significant variation on the important design parameters. The grid sensitivity study has been performed carefully for a typical aspect ratio (AR) of 2 and Re = 100 with 20% central restriction (CR). Several test cases are run by using different grid size to quantify grid independence study in terms of magnitude and location of Ψmax. Finally in our work we have considered the meshes comprising of 41 × 37 grid nodes in the inlet section and 221 × 121 grid nodes in the exit section in the x- and y-directions, respectively. For higher aspect ratio like AR = 4, 5 and 6, the grid sensitivity study has been performed considering typical aspect ratio of 5, Reynolds number of 100% and 20% central restriction. For these aspect ratios, the non-dimensional inlet and the exit lengths are considered as 1 and 200 respectively. The meshes comprising of 41 × 37 grid nodes in the inlet section and 457 × 193 grid for the exit section in the x- and y-directions, respectively are used. This study has been discussed in detail by Das and Chakrabarti [13] .
2.4. Code Validation
Sheen et al. [5] have performed the experimental work to study the flow pattern for an annular flow over an axisymmetric sudden expansion configuration with central restriction at inlet section. From their results, the mean axial velocity profile at the exit of the annular region for Re of 326 AR of 1.987 and CR of 47.9% in case of laminar flow region has been considered by us for the validation purpose of our results at the same typical magnitudes of Re, AR and CR. The results of our numerical computation and work of Sheen et al. [5] have been presented in Figure 2. The figure shows good agreement between our numerical results and the results obtained by Sheen et al. [5] in their experimental work.
Battaglia and Papadopoulos [14] have performed a 2-D numerical study considering a symmetric sudden expansion channel. Their results are used for the purpose of validation of our results for a fixed Reynolds number of 171. During analysis, two different aspect ratios of 1.61 and 2 are used. This is shown in Table 1 and Table 2 respectively. The dimensionless reattachment length based on inlet and exit dimensions are compared between our computational results and the results of Battaglia and Papadopoulos [14] . The results show a good agreement except the small deviation.
3. Results and Discussion
The important results of the present study are reported in this section. The parameters those affect the flow characteristics are identified as,
![]()
Figure 2. Comparisons between numerical and experimental velocity values.
![]()
Table 1. Comparison of non-dimensional reattachment length for Re = 171, based on inlet dimension.
![]()
Table 2. Comparison of non-dimensional reattachment length for Re = 171, based on outlet dimension.
a) Reynolds number, 50 ≤ Re ≤ 200,
b) Central restriction, CR = 0 to 40%,
c) Suction, S = 2% to 10% of inlet mass flow,
d) Aspect ratio, AR = 2 to 6.
3.1. Average Static Pressure Distribution Along the Axial Distance
A sudden expansion configuration creates a separation of the boundary layer from the wall which results positive and negative pressure zone at the post throat region. This post throat region greatly influence the static pressure which is considered an important parameter in assessing the performance of various components of gas turbine engine such as diffuser, combustor etc. In the present work, the average static pressure at any cross section is determined by the following expression:
![]() . (4)
. (4)
The average static pressure distribution curves along the axial distance for sudden expansion with 40% central restriction with 0% (i.e. without suction), 2%, 4%, 6%, 8% and 10% suction are shown in Figure 3(a). For all the cases, a fixed Reynolds number of 100 with a constant aspect ratio of 2 are considered. The general characteristics of all the curves are that in the inlet section the steep fall of average static pressure takes place at the throat. This is an expected behavior because, across the throat region, there is a sudden increase in area which enhances the denominator of the above expression sharply, and presumably no amount of static pressure recovery across the region can compensate the steep fall of average static pressure. Then, at the post throat region, at a given section there are zones of positive pressure and negative pressure. The combination effect of positive and negative pressure zones, give significant pressure recovery within the main stream due to increased kinetic energy diffusion. After reaching the maximum value, the average static pressure gradually droops due to dominating frictional effect for the rest of the region. From the figure, it is noted that the maximum magnitude of average static pressure rise from throat increases with increase in percentage of suction. Again, at a particular value of
Reynolds number and aspect ratio, the magnitude of average static pressure rise at a section is more in case of sudden expansion with central restriction and suction configuration compared to the case of configuration of sudden expansion with central restriction only. The probable reason may be that, when suction is considered the recirculating bubble size decreases. Because of that, the effect of diffusion should decrease. But, suction at the top of the vertical wall decreases the outer layer of corner recirculation zone which are the main cause of dominating frictional effect with the wall. This combined effect increases the magnitude of average static pressure at any section. The effect of central restriction on average static pressure distribution along the axial distance for sudden expansion with different percentages of central restrictions and 10% suction and without suction configurations is illustrated in Figure 3(b). In each case, different central restrictions are considered as 0% (i.e. plain sudden expansion), 20%, and 40% for a fixed Reynolds number of 200 with a constant aspect ratio of 2. It is noted that the maximum magnitude of average static pressure rise from throat increases with increase in percentage of central restriction for both with and without suction configurations. It may be attributed that the larger zone of diffusion with increase in central restriction may cause the enhancement of static pressure rise. It is also observed that, at any section the magnitude of average static pressure rise is more for the case of suction configuration compared to without suction configuration. The reason is explained earlier in this subsection. Figure 3(c) represents the average static pressure distribution along the axial distance for sudden expansion with typically 40% central restriction with and without suction configuration for typical Reynolds numbers of 50, 100, 150 and 200 to investigate the effect of Reynolds number on average static pressure rise for stated configurations. In each case, a fixed aspect ratio of 2 is considered. It is seen that the maximum average static pressure rise from throat increases with increase in Reynolds number for both the configurations with and without suction. The reason is that the kinetic energy diffusion increases with increase in Reynolds number.
When sudden expansion with central restriction with and without suction configurations are compared, maximum magnitude of average static pressure rise from throat is always more in case of suction configuration compared to without suction one for a fixed value of Reynolds number. The effect of aspect ratio on average static pressure distribution with axial distance for sudden expansion with typically 40% central restriction and sudden expansion with typically 40% central restriction for 10% suction is presented in Figure 3(d). For all the cases, different aspect ratios of 2, 4 and 6 are considered with a fixed Reynolds number of 200. At this higher percentage of central restriction (i.e., CR = 40%), it is noted that the maximum magnitude of average static pressure rise from throat is always less for higher aspect ratio. From the figure, it is also observed that at a particular value of aspect ratio the maximum magnitude of average static pressure rise from throat is always more in case of suction configuration compared to without suction.
Therefore, from the study, it may be mentioned that sudden expansion with central restriction and suction configuration will give more benefit in terms of the maximum magnitude of average static pressure rise from throat compared to the sudden expansion with central restriction configuration only or configuration of plain sudden expansion.
3.2. Average Stagnation Pressure Distribution Along the Axial Distance
Stagnation pressure is one of the important parameter to determine the performance of the various components of a gas turbine cycle as well as the cycle itself. The computation of average stagnation pressure at any section should take into considerations of the direction of the velocity vector particularly in a flow situation, like the present case where the flow is the recirculating type. After performing the energy balance, Chakrabarti et al. [15] have developed the following mathematical formulation to estimate the stagnation pressure at a particular cross section;
![]() . (5)
. (5)
The suffix “e” represents the plane of measurement. Stagnation pressure is constant in a stream flowing without heat or work transfer only if friction is absent, i.e., the stagnation pressure drop can be used as a measure of fluid friction. In the present problem the stagnation pressure at any location is computed using the dimensionless form of the above equation. It is obvious that according to the present definition, average stagnation pressure, should always drop along the axial length.
The average stagnation pressure distribution along the axis has been described in Figure 4(a) for 0% (without suction), 2%, 4%, 6%, 8% and 10% suction of inlet mass flow. The general behaviour of all curves is drooping characteristics for both the configurations (with and without suction). From the figure, it is noted that average stagnation pressure drop increases at any section with increase in percentage of suction. As Reynolds number is fixed for the considered cases, kinetic energy diffusion may decrease slightly or remains more or less same because of increase in suction. Again, it is expected that size of the recirculating bubble at corner zone decreases with increase in suction. This may decrease the viscous dissipative effect slightly. Finally, the viscous dissipative effect dominates the effect of diffusion as percentage of suction increases and this leads to increase in average stagnation pressure drop at any section. The average stagnation pressure distribution with axial distance has been computed for sudden expansion with 0% (i.e. plain sudden expansion), 20%, and 40% central restrictions considering 10% suction and without suction configurations for a typical Reynolds number of 200 and an aspect ratio of 2. The outcome of the exercise has been depicted in Figure 4(b). From the study, it is seen that, for a
fixed value of Reynolds number, the average stagnation pressure drop at any section increases with increase in percentage of central restriction for both the configurations. This is happening because, with increase in percentage of central restriction, the viscous dissipative effect dominates the effect of kinetic energy diffusion, this leads to increase in average stagnation pressure drop at a section. It is also noted that, at a particular value of Reynolds number and central restriction, more stagnation pressure drop occurs at a section in case of suction configuration compared to without suction configuration. The reason is explained earlier in this subsection. The effect of Reynolds number on average stagnation pressure distribution along the axis for sudden expansion with typically 40% central restriction only and sudden expansion with typically 40% central restriction and 10% suction has been investigated and illustrated in Figure 4(c). The Reynolds numbers are considered as 50, 100, 150 and 200 for a particular aspect ratio of 2.
The general characteristics of all the curves of both the considered configurations (i.e., with and without suction) are same in nature, i.e., average stagnation pressure drop at a section decreases with increase in Reynolds number. This can be reasoned as, for higher Reynolds number flow, the kinetic energy contribution towards the working fluid at a section will be higher leading to the possibility of higher average stagnation pressure at that section. Form the figure, it is also found that for all the considered Reynolds number, the average stagnation pressure drop at a section is more in case of sudden expansion with central restriction and suction configuration compared to the case of sudden expansion with central restriction only, like earlier observation. The reason is explained earlier. The variation of average stagnation pressure distribution along the axial distance for different aspect ratio of 2, 4 and 6 for sudden expansion with 40% central restriction and sudden expansion with 40% central restriction and 10% suction is shown in Figure 4(d). In each case, a typical Reynolds number of 200 is used. It is noted that the average stagnation pressure drop at a section increases with increase in aspect ratio for both the considered configurations. The reason is that as the distance from the throat increases, the frictional loss increases for higher aspect ratio due to larger size of recirculating bubble at corner zone. This increased frictional loss enhances the average stagnation pressure drop at a section. Like earlier observation, it is again noted that the average stagnation pressure drop at a section is more in case of suction configuration compared to the configuration of without suction.
4. Conclusions
In many flow situations, fluid is decelerated to ensure an increase in the static pressure and to get the recirculating bubbles for the mixing of two or several fluids as a mixing chamber in the decelerated zone. Among its many applications, particular mention may be made of the function as a diffuser, or mixing chamber and combustor. In this research activity, the effects of percentage of suction, percentage of central restriction, Reynolds number and aspect ratio on average static pressure distribution and average stagnation pressure distribution have been investigated for the configuration of sudden expansion with central restriction and suction configuration. This leads to the following important observations:
1) Maximum magnitude of average static pressure rise from throat increases with the increase in percentage of suction. This maximum magnitude also increases with the increase in Reynolds number and percentage of central restriction. The maximum magnitude of average static pressure rise from throat is less for higher aspect ratio. Again, this magnitude is always more in case of sudden expansion with central restriction and suction configuration compared to the case of without suction configuration.
2) Average stagnation pressure drop at any section increases with the increase in percentage of suction and percentage of central restriction, but it decreases with the increase in Reynolds number. The average stagnation pressure drop at a section increases with the increase in aspect ratio. When suction is considered, average stagnation pressure drop at a section increases in case of suction configuration compared to the case of without suction.
Nomenclature
Li: Inlet length (i.e., length between inlet and throat sections), m
Lex: Exit length (i.e., length between throat and exit sections), m
LR: Reattachment length, m
p: Static pressure, [N/m2]
Re: Reynolds Number
u: Velocity in x-direction, m∙s−1
v: Velocity in y-direction, m∙s−1
U: Average velocity, m∙s−1
W: Width of central restriction, m
Ws: Width of suction slot, m
W1: Width of inlet duct, m
W2: Width of exit duct, m
AR: Aspect ratio = W2/W1
CR: Percentage of central restriction = W/W1
x, y: Cartesian co-ordinates
ρ: Density, kg∙m−3
μ: Dynamic viscosity, kg∙m−1∙s−1
Subscripts
*: Dimensionless terms
1-1: Inlet
2-2: Exit
NOTES
![]()
*Corresponding author.