Two Eigenvector Theorems

Raghuram Prasad Dasaradhi^1*, V. V. Haragopal²

¹Department of Mathematics, Osmania University, Hyderabad, India.
²Department of Statistics, Osmania University, Hyderabad, India.

DOI: 10.4236/alamt.2016.61002                

Abstract

In this paper, we established a connection between a square matrix “A” of order “n” and a matrix  defined through a new approach of the recursion relation . (where  is any column matrix with n real elements). Now the new matrix  gives us a characteristic equation of matrix A and we can find the exact determination of Eigenvalues and its Eigenvectors of the matrix A. This new approach was invented by using Two eigenvector theorems along with some examples. In the subsequent paper we apply this approach by considering some examples on this invention.

Keywords

Characteristic Equation, Minimal Polynomial, Eigenvalues, Eigenvectors, Vander Monde Matrix, Jacobi Block Matrix

Received 19 December 2015; accepted 5 March 2016; published 8 March 2016

1. Introduction

In this article, we present results connecting the Eigenvalues and vectors [1] - [5] of a square matrix “A” of order “n” and a matrix 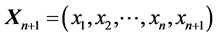defined (where x₁ is any column matrix with n elements) through the recursion relation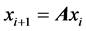. these results will be useful in the context of exact determination of Eigenvectors of a matrix associated with a specific Eigenvalue when the minimal polynomial is known. However this problem, of considerable interest in the field of numerical matrix analysis, is being considered in a separate study.

2 Basic Points

Before presenting these Eigenvector theorems, it is useful to introduce a few notations and some rather obvious lemmas.

Let A be a matrix with n Eigenvalues 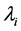and associated Eigenvectors 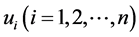Unless stated otherwise, these roots are assumed to be distinct. Similarly we define the minimal (and under the assumption of distinctness, also the characteristic) Polynomial [6] of A.

: a set of distinct indices’s, a subset of set.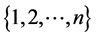

: the vector of n components of the coefficients of 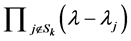in reverse order, with trailing zeroes.

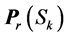: the same vector as 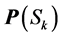but with leading zeroes;

When, a singleton, we shall write.

: the Vander monde matrix [7] , defined by,.

: an nth order matrix with the following structure. The column, has the last element as, successive elements of from below being obtained by accumulating successive terms in the expansion of.

: the left justified n-component vector of coefficients of in the reverse order.

: same vector as q above, but with S leading zeroes.

J: the Jacobi Block matrix [7] [8] with diagonal elements and super diagonal elements1

: the j-th column of the identity matrix.

: appropriate scalars as need be.

3. Main Results

The following useful lemmas are rather obvious:

LEMMA 1:

LEMMA 2:

LEMMA 3:

LEMMA 4:

For clarity we shall illustrate these notations and results by way of illustrations.

ILLUSTRATION 0:

let;.

Now for the

3.1. First Eigenvector Theorem

Let

where, then. Proof is obvious once it is noted that if, then

Since eigenvectors are unique up to scale, it is obvious that, by proper scaling one can always have, For arbitrary, the relation (provided of-course tha lies in the full-space, but in no Proper subspace) with the set as basis.

COROLLARY 1.1:

COROLLARY 1.2:

COROLLARY 1.3:

COROLLARY 1.4: Let be a pair of complex conjugate Eigenvalues of A and Let be the associated Eigenvectors where u, v are real vectors.

Let.

Then and.

Another analogous corollary, in respect of Eigenvalues where is a surd is obvious.

ILLUSTRATION 1.1:

let and

Then;

.

Hence

and

U. diag

Let.

Then,

And

where,

ILLUSTRATION 1.2:

Let and

We have

A has as one real root and as two complex conjugate roots.

Hence is the Eigenvector for.

from which we get the complex conjugate Eigen vectors

where;.

We shall now state

3.2. The Second Eigenvector Theorem (The Generalized Eigenvector Theorem)

Let; then and hence.

Proof is obvious once it is observed that.

ILLUSTRATION 2:

Let and

We have the minimal polynomial of degree 3, as,

This is also the characteristic polynomial.

Hence

where

, , are such that;

, and.

taking

where,

We get

where

4. Summary

Extensions of these two theorems and their corollaries to cases where the minimal polynomial is a proper factor of the characteristic polynomial and hence, for some of the multiple Eigenvalues at least, the associated Eigenspace is of dimension more than one is obvious though explicit proof is slightly cumbersome.

The proposed method can be used in many mathematical subsequence applications viz., in most of the big data analysis, image processing and multivariate data analysis.

Acknowledgements

We are highly thankful to Late Prof. S.N. NARAHARI PANDIT for suggesting this problem, we are indebted to him.

Thanks to UGC-India, for financial support.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Dasaradhi, R.P. and Haragopal, V.V. (2015) On Exact Determination of Eigen Vectors. Advances in Linear Algebra & Matrix Theory, 5, 46-53 http://dx.doi.org/10.4236/alamt.2015.52005
[2]	Liu, B.L. and Lai, H.-J. (2000) Matrices in Combinatorics and Graph Theory. Kluwer Academic Publishers.
[3]	Proskuryakov, I.V. (1978) Problems in Linear Algebra. Mir Publishers, Moscow.
[4]	Datta, K.B. (1991) Matrix and Linear Algebra. Prentice-Hall of India Private Limited, New Delhi.
[5]	Horn, R.A. and Johnson, C.R. (1991) Topics in Matrix Analysis. Cambridge University Press, Cambridge.
[6]	Cullen, C.G. (1990) Matrices and Linear Transformations. 2nd Edition, Dover Publications, New York.
[7]	Bellman, R. (1974) Introduction to Matrix Analysis. 2nd Edition, Tata Mcgraw-Hill Publishing Company Ltd., New Delhi.
[8]	Curtis, C.W. (1984) Linear Algebra: An Introductory Approach. Springer-Verlag, New York.