Intelligent Winding Machine of Plastic Films for Preventing Both Wrinkles and Slippages ()
Received 30 July 2015; accepted 16 February 2016; published 19 February 2016

1. Introduction
Thin, flexible plastic films (webs) are widely used in various fields as different materials, including functional and packaging materials. Common examples include the optical films used in liquid-crystal displays (LCD) and packaging films used for the storage and transport of foods. The reason for this is that webs are suited to use in mass production and can be given moisture proofing, light blocking, optical properties, and such in a continuous process. In general, during the final web handling process, the web is rewound into a roll using a rewinding system. Finally, the rewound web is cut to the appropriate size in making the final product and shipped. Therefore, it is extremely important to prevent defects during rewinding in order to maintain the quality of the web. When rewinding condition settings are inappropriate, however, defects such as slip, telescoping, and wrinkles will occur in the rewound roll. These types of defects are closely related to the internal stress condition of the roll. As such, we believe that by theoretically determining the internal stress, we can predict and prevent such defects ahead of time. In this light, Hashimoto et al. have proposed a rewinding tension optimization method designed to prevent slip and wrinkles inside the roll [1] -[3] . We have not found any examples, however, in which software for determining the optimal rewinding conditions has been specifically integrated with the actual rewinding equipment.
In this research, we investigate the optimal rewinding conditions, including tension and nip-load, and developed a rewinding system in which the software is integrated to minimize rewinding defects.
2. Tension and Nip-Load Optimization Function
2.1. Equipment Subject to Optimization
Figure 1 shows a schematic of the web-based manufacturing machine that is the subject of this research. The machine is composed of an unwinding unit, a coating (printing) unit, a drying unit, and a rewinding unit.
The web is fed from the unwinding unit and transported to the rewinding unit, where it is ultimately rewound into a roll. Moreover, processes located between the unwinding and rewinding units, such as printing and coating, are used to provide the web with various properties.
Such production processes are used widely for such applications as printing of webs for food packaging and coating and drying of functional materials on webs to produce LCDs and lithium-ion batteries.
In this research, we focused on the rewinding unit―in which defects are particularly likely to occur―and investigated the commonly used dual-shaft turret rewinder shown in Figure 2.
![]()
Figure 1. An example of the manufacturing equipment.
2.2. Applying the Rewinding Model to an Actual Rewinder
2.2.1. Web Rewinding Model
In this research, we predict the occurrence of defects by first theoretically determining the internal roll stress, from which we determine the optimal rewinding conditions. Therefore, to determine the internal roll stress, we assume the web that has been wound into a spiral to be a series of thin walled concentric cylinders, such as that shown in Figure 3. The wound roll model consists of alternating layers of web and air film entrained between the web layers.
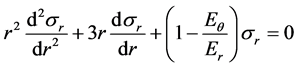 (1)
(1)
When solving for Equation (1), we need to set the following two boundary conditions for radial stress σr. First, we can define the following equation for the boundary condition at the innermost layer, given that displacement at the first layer of the web and at the core are equal.
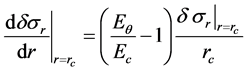 (2)
(2)
Meanwhile, we can define the following equation for the boundary condition at the outermost layer of the roll during rewinding.
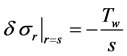 (3)
(3)
Because there is no new web added to the outermost layer at the completion of rewinding, we can define the boundary condition at the outermost layer as follows:
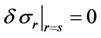 (4)
(4)
By applying the boundary conditions shown in Equations (2) through (4) and solving for rewinding equation (1), we can determine the internal radial stress. At this point, we can determine radial stress σri at the i-th layer of the roll by adding the stress increment from the (i+1) layer to the n-th layer (final roll layer) as in Equation (5).
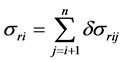 (5)
(5)
Here, δσrij expresses the stress increment at the j-th layer when the web is wound to i layers. During specific calculations, we successively solve the rewinding equation for stress increment δσr obtained by substituting
Equation (5) into Equation (1) under boundary conditions (2) through (4) and repeating in compliance with Equation (5).
Moreover, under most manufacturing conditions, the region where the internal tangential stress becomes negative (compressive stress), in other words, the region in which wrinkles form, has a higher likelihood of occurring near the roll core. Because this phenomenon is often experienced in manufacturing plants, we must accurately estimate the internal stress near the roll core to prevent such wrinkles. In the actual machine, however, phenomena can occur that create disturbance near the rewinding core at the outset of web winding, so the approach does not necessarily satisfy the boundary conditions mentioned earlier. Some of these typical phenomena include tension variation in the web width direction caused by geometric steps in the rewinding core and adhesive tape, or by variation in adhesion and wrinkling in the web.
These phenomena cause variation in internal roll stress in the width direction, sometimes causing the web to be rewound on the roll core in a distorted geometry. When these types of phenomena occur near the roll core, the internal stress in the width direction will be uneven through the outermost layer because the web is successively layered. Wrinkles that occur at the outset of rewinding are different from wrinkles caused by internal roll compressive stress, and are thus difficult to improve using tension and nip-load.
Therefore, we investigated a method of avoiding these defect phenomena that conforms with the boundary conditions in order to apply the theoretical rewinding model mentioned earlier to the actual machine.
2.2.2. Tapeless Web Splicing Method
Web splicing during rewinding typically uses adhesive tape, as shown in Figure 4, so differences in adhesion between the roll core and adhesive tape are likely to cause width direction tension variation in the web. Moreover, as the roll diameter increases, a high radial stress occurs near the innermost layers of the roll, meaning that thickness variation in the adhesive tape increases the risk of generating an uneven stress profile in the web width direction. To avoid this type of defect, we must consider the influence that the position and thickness of the adhesive tape will have on the internal roll stress ahead of time and ensure that wrinkles do not occur in the web immediately before rewinding. The condition of the web during transport, however, contains many items that cannot be numerically compared. Moreover, there are various types of adhesive tapes, so it is nearly impossible to quantitatively handle these characteristics. Therefore, for the rewinding machine used in this research, we selected a machine that uses a water droplet spray (tapeless method)―an example of which is shown in Figure 5―instead of one that uses an adhesive tape.
Figure 6 compares the experimental results of the tapeless method proposed in this research and the conventional adhesive tape method. In the experiment, a web of PET film was rewound to a maximum roll diameter of 200 (mm). During rewinding, we inserted a pressure sensitive paper when the roll diameter reached 100 (mm) to visually observe the stress profile in the width direction after rewinding. The photograph shows the results when the web was later unwound. From the results, we confirmed changes in internal stress and wrinkles when using an adhesive tape, whereas we did not observe any wrinkles or changes in stress when using the tapeless method. Therefore, we concluded that it is possible to prevent wrinkles at the outset of rewinding mentioned earlier using the tapeless method.
![]()
Figure 5. Photograph of spray nozzle device.
2.3. Optimizing Rewinding Conditions
2.3.1. Concept behind Rewinding Condition Optimization
In actual manufacturing lines, the web width, thickness, and mechanical properties often differ depending on the item being produced. As such, it is desirable if the rewinding tension and nip-load can be set over a wide range. Conventionally, rewinding conditions are set based on experience, while a method for proportionally decreasing tension in the roll radial direction under a constant nip-load (taper tension), in particular, has come to be used widely. As will be mentioned later, however, a rewinding method that increases the final winding tension is more useful to realize rewinding conditions that maintain an optimal internal roll stress condition. Meanwhile, it is believed to be important to variably control the entrained air volume to maintain the optimal roll quality using nip-load, so a system that strictly fixes the running conditions is not flexible enough. Therefore, in this research, we selected a method that indicates the rewinding conditions using the calculation model mentioned earlier, as shown in Figure 7.
2.3.2. Setting Method for Optimal Rewinding Conditions
We used a standard computer in optimizing the rewinding conditions. The software is composed of two main parts―a user interface that displays the precondition settings necessary for optimization along with the calculation results, and a calculation unit that provides the computational analysis for optimization. Confirmation of the precondition settings and calculation results is best when the operational method relies on the experience of the operator as little as possible. As such, we used a method that visually displays these using graphs and such. Figure 8 shows an example of the results. Here, we can set the web’s physical properties by using the input screen shown in Figure 8(a). Using this approach, the accuracy of the rewinding conditions optimized in the calculation unit can be visually confirmed using graphs, such as those shown in Figure 8(b).
2.3.3. Optimization Method Summary
The rewinding tension obtained via optimization is converted to a torque command value and applied to an electric motor through the control unit. The nip-load obtained via optimization is converted to an equivalent pressure and applied by the control device as a command value. The rewinding tension and nip-load are expressed as the following design variable vector.
 (6)
(6)
Here, ΔTi 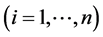 and ΔNj
and ΔNj 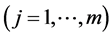 are the updated values from the initial tension and initial nip-load, respectively. i and j express the radial boundary position. The tension function and nip-load function are determined via interpolation of these values, such as by the third order spline function for radial coordinate r. Moreover, the search range for the design variable vector is selected with an upper limit of maximum tension Twmax and maximum nip-load Nmax, and a lower limit of minimum tension Twmin and minimum nip-load Nmin. These values are determined ahead of time by the designer.
are the updated values from the initial tension and initial nip-load, respectively. i and j express the radial boundary position. The tension function and nip-load function are determined via interpolation of these values, such as by the third order spline function for radial coordinate r. Moreover, the search range for the design variable vector is selected with an upper limit of maximum tension Twmax and maximum nip-load Nmax, and a lower limit of minimum tension Twmin and minimum nip-load Nmin. These values are determined ahead of time by the designer.
To prevent web wrinkles, it is necessary to prevent the circumferential stress from becoming compressive. As such, we impose a condition where the minimum circumferential stress is a non-negative. At the same time, to prevent slip, it is necessary to ensure that web interlayer friction remains greater than critical friction Fcr at which slip begins.
![]()
Figure 7. Schematic diagram of the system.
![]() (a)
(a)![]() (b)
(b)
Figure 8. An example of interface. (a) Input data. (b) Calculation result.
Considering the above factors, we express the constraint conditions as the following inequality.
![]() (7)
(7)
Here, constraint function gi(X) is defined by each of the following equations.
![]() (8)
(8)
When designing the objective function, we set the circumferential stress to be a non-negative close to zero, and set the difference between interlayer friction and critical friction to be a positive close to that approaching zero over a wide range of radial positions in the roll. Moreover, we set the difference between stress at the start of rewinding and at the end of rewinding as close to zero as possible to ensure stability during web splicing. Therefore, the objective function that must be minimized is defined by the following equation.
![]() (9)
(9)
Moreover, interlayer friction F(r) is determined by Equation (10). Circumferential stress σθref is a physical value introduced for purposes of scaling and is given by Equation (11).
![]() (10)
(10)
![]() (11)
(11)
Given the above, the optimized problem for rewinding tension and nip-load is formularized by the following equation.
![]() (12)
(12)
3. Overall Evaluation of the Research Machine
We conducted rewinding tests to investigate the applicability of the rewinding condition optimization method proposed above and confirmed the performance. We calculated the optimal rewinding conditions using this optimization method and observed the appearance of a roll rewound under these rewinding conditions. Table 1 shows the applied conditions during optimization. Moreover, the applied conditions are values that can be modified accordingly depending on the specifications during production.
Figure 9 shows a concrete example of an optimization calculation for rewinding tension and nip load. In Figure 9(a), the dashed line shows rewinding tension for an initial tension of Tw0 = 200 (N/m) (taper tension), the dash-dot line shows rewinding tension for an initial tension of Tw0 = 140 (N/m) (taper tension), and the solid line shows the optimized rewinding tension. On the other hand, Figure 9(b) shows the nip-load for each of the tensions shown in Figure 9(a). Figure 9(c) shows the tangential stress and Figure 9(d) shows the interlayer
![]()
Figure 9. Internal stress under conventional conditions and optimized conditions.
friction. In Figure 9(a), the taper tension is given a reduction rate of 30 (%). This value is determined based on the wrinkle and slip occurrence conditions, and has come into broad use through trial and error. Moreover, the nip-load for the taper tensions in Figure 9(b) is N = 70 (N/m) (an empirically determined fixed value).
As can be seen from Figure 9(c), when using the non-optimized tension (dashed line), we can see that there is a region in which the tangential stress becomes negative (r/rc = 1.1 to 2.5), a region in which there is a high risk of wrinkle generation [1] [2] .
This is equivalent to a condition of so-called roll tightening. Meanwhile, when using the optimized tension and nip-load (solid line), we see that there is no compression stress in any of the regions.
Figure 9(d) shows the interlayer friction. The higher the value, the less likely it is for the web slip phenomenon called telescoping to occur. From Figure 9(d), we see that using the optimized rewinding conditions (solid line) maintains a higher friction than with the conventional rewinding conditions (dot-dash line). In short, if an equivalent external force is generated in the web handling environment, we see that this approach is also more effective than the conventional method at preventing telescoping. Conventionally, when telescoping occurs where taper tension is applied, the solution is to set a high value for the initial tension or a high value for the nip-load. In this case, radial stress σr, which acts as the web interlayer pressing force, increases so that the air layer formed between the web layers becomes thinner, increasing interlayer friction. At the same time, however, compressive stress is generated in circumferential stress σθ, which risks causing wrinkles. Meanwhile, using the optimization models in this research, we set the rewinding tension after estimating the tangential stress (compressive stress), used nip-load to constrain the entrained air volume near the outermost layers where the pressing force (radial stress) decreases, and set a high value for the interlayer friction. Moreover, another approach is to use a fixed value for the nip-load and increase the rewinding tension near the outermost layers, but a high tensile force risks causing the creep phenomenon to occur in the web. In addition, given limitations on the cost of the electric motors and installation space, it is not always possible to increase the rewinding tension. As such, it is desirable to use a variable nip-load in actual manufacturing locations.
Although we showed that we can calculate the optimized rewinding conditions using these types of optimization models, we also made an appearance comparison of rewound webs to confirm its applicability to real-world situations.
Figure 10 shows a photograph of two rewound webs. The rewinding conditions and web conditions are equivalent to the conditions shown in Figure 9 and Table 1. In Figure 10(b), we can see that there are no wrinkles when the optimal rewinding conditions are applied. In contrast, as shown in Figure 10(a), wrinkles occur near the roll core under conventional rewinding conditions. Even though wrinkles may not be easy to confirm visually, with functional materials such invisible wrinkles often make the quality of the product unacceptable.
As such, it is important to theoretically ensure that the internal roll stress will be non-negative before rewinding.
Next, we conducted drop tests to compare the slip resistance force. Figure 11 shows a schematic of the drop test. This device has a structure that drops the roll along a shaft. In this test, we ensured free-fall from the same height for rolls rewound at each tension and compared the appearance after impact.
Figure 12 shows the appearance of the rolls after falling. With the roll rewound using the conventional rewinding conditions, as shown in Figure 12(a), we see that slip occurs at the innermost layers. The reason for this is that the interlayer friction force is relatively lower than the impact force when the bottom face of the roll core impacts the ground. On the other hand, with the roll rewound at the optimized rewinding conditions, as shown in Figure 12(b), we can see that there is no slip even when an impact force is applied. In other words, we can see that these conditions make it more difficult for slip to occur without causing internal wrinkles than with the conventional method. From the above, we were able to verify the viability of the adaptation method of this optimization model with an actual rewinding machine.
![]()
Figure 11. Experimental apparatus for drop test.
4. Conclusions
In this paper, we created a simple rewinding condition setting system that considers the standard properties that a rewinding machine must meet in applying the rewinding condition optimization method. The following summarizes our main conclusions.
1) We created a tapeless system to suitably operate the rewinding model and showed the results.
2) We integrated the optimizing function for rewinding tension and nip-load into an actual rewinder in creating a method for easy operation by the operator [6] [7] .
3) We showed that the optimization function was able to effectively prevent defects, such as telescoping and wrinkles.
Nomenclature
Ec: rewinding core Young’s modulus (Pa)
Er: wound roll radial Young’s modulus considering influence of entrained air (Pa)
Eθ: wound roll circumferential Young’s modulus (Pa)
f(X): objective function
Fcr: critical friction reference value (N)
F: interlayer web friction (N)
![]() : limiting function
: limiting function
hw: web thickness (m)
m: nip-load function radial partitions
N: nip line load (N/m)
n: tension function radial partitions
![]() : nip-load change from initial nip load at j-th nodal point (N/m)
: nip-load change from initial nip load at j-th nodal point (N/m)
![]() : maximum tolerance value of nip-load change at j-th nodal point (N/m)
: maximum tolerance value of nip-load change at j-th nodal point (N/m)
![]() : minimum tolerance value of nip-load change at j-th nodal point (N/m)
: minimum tolerance value of nip-load change at j-th nodal point (N/m)
r: arbitrary radial position on roll layer (m)
rc: core radius (m)
s: wound roll outer radius (m)
Tw0: initial rewinding tension (N/m)
Tw: rewinding tension
![]() : change in tension from initial tension at i-th nodal point (N/m)
: change in tension from initial tension at i-th nodal point (N/m)
![]() : maximum tolerance value for tension change at i-th nodal point (N/m)
: maximum tolerance value for tension change at i-th nodal point (N/m)
![]() : minimum tolerance value for tension change at i-th nodal point (N/m)
: minimum tolerance value for tension change at i-th nodal point (N/m)
W: web width, m
V: web rewinding velocity (m/min)
X: design variable vector
σmin: minimum wound roll tangential stress (Pa)
σr: wound roll internal radial stress (Pa)
δσr: wound roll radial stress incremental (Pa)
σθ: internal roll circumferential stress (Pa)
σθref: circumferential stress reference value (Pa) (=Tw0/hw)