Two-Temperature Generalized Thermoelasticity without Energy Dissipation of Infinite Medium with Spherical Cavity Thermally Excited by Time Exponentially Decaying Laser Pulse ()
Received 14 December 2015; accepted 24 January 2016; published 27 January 2016

1. Introduction
The two temperatures theory of thermoelasticity was introduced by Gurtin and Williams [1] , Chen and Gurtin [2] , and Chen et al. [3] , [4] , in which the classical Clausius-Duhem inequality was replaced by another one depending on two temperatures; the conductive temperature  and the thermodynamic temperature
and the thermodynamic temperature , the first is due to the thermal processes, and the second is due to the mechanical processes inherent between the particles and the layers of elastic material, this theory was also investigated by Ieşan [5] .
, the first is due to the thermal processes, and the second is due to the mechanical processes inherent between the particles and the layers of elastic material, this theory was also investigated by Ieşan [5] .
Among the authors who contribute to developing this theory, Quintanilla studied existence, structural stability, convergence and spatial behavior for this theory [6] , Youssef constructed the generalized Fourier’s law to the two-temperature theory of thermoelasticity and proved its uniqueness of solution for homogeneous isotropic material [7] . Puri and Jordan studied the propagation of plane harmonicwaves, recently [8] , Magaña and Quintanilla [9] have studied the uniqueness and growth solutions for the model proposed by Youssef [7] . A new theory of generalized thermoelasticity has been constructed based on two-temperature generalized thermo- elasticity theory for anisotropic and homogeneous body without energy dissipation by Youssef [10] . This new theorem has been constructed in the context of Green and Naghdi model of type II of linear thermoelasticity. Also, a theorem of general uniqueness is proved for two-temperature generalized thermoelasticity without energy dissipation [10] .
The present paper is devoted to a study of the induced temperature and stress fields in aninfinite elastic medium with aspherical cavity under the purview of two-temperature thermoelasticity without energy dissipation. The medium is considered to be an isotropic homogeneous thermoelastic material. The bounding plane surface of the cavity is thermally loaded bytime exponentially decaying laser pulse. An exact solutions of the problem is obtained in Laplace transformdomain, and the inversions of the Laplace transforms have been culculated numerically. The derived formulations are computed numerically for copper, and the results are presented in graphical form.
2. The Governing Equations
We will consider perfectly conducting, elastic, isotropic, and homogeneous medium and the governing equations will be taken in the context of two-temperature generalized thermoelasticity without energy dissipation.
According to Youssef model, the heat conduction equation takes the form [10] :
 ,
,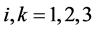 (1)
(1)
The conduction-dynamical heat equation takes the form [10] :
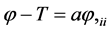 (2)
(2)
The equations of motion take the form
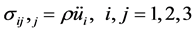 (3)
(3)
The constitutive equations take the form
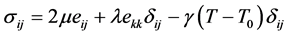 (4)
(4)
and
 (5)
(5)
where 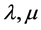 Lame’s constants,
Lame’s constants, 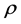 density,
density,  specific heat at constant strain,
specific heat at constant strain,  ,
, 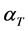 coefficient of linear thermal expansion,
coefficient of linear thermal expansion,  is the time,
is the time, 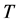 is the temperature,
is the temperature, ![]() is the reference temperature,
is the reference temperature, ![]() is the thermodynamical temperature increment such that
is the thermodynamical temperature increment such that![]() ,
, ![]() is the conductive heat
is the conductive heat
temperature, ![]() are the components of stress tensor,
are the components of stress tensor, ![]() is the cubic dilatation,
is the cubic dilatation, ![]() is the displacement components,
is the displacement components, ![]() is the characteristic of Green-Naghdi theorem, a is non-negative parameter (two- temperature parameter), and Q is the heat source per unit mass.
is the characteristic of Green-Naghdi theorem, a is non-negative parameter (two- temperature parameter), and Q is the heat source per unit mass.
3. Formulation of the Problem
We will consider perfectly conducting elastic infinite bodies with spherical cavity occupy the region ![]() of an isotropic homogeneous medium whose state can be written in terms of the space variable r and the time variable t such that all of the field functions vanish at infinity. We use a spherical system of coordinates
of an isotropic homogeneous medium whose state can be written in terms of the space variable r and the time variable t such that all of the field functions vanish at infinity. We use a spherical system of coordinates![]() . Due to its symmetric geometry, the problem is one-dimensional with all the functions considered depending on the radial distance r and the time t and the displacement
. Due to its symmetric geometry, the problem is one-dimensional with all the functions considered depending on the radial distance r and the time t and the displacement![]() . It is assumed that there are nobody forces in the medium and it is initially quiescent.
. It is assumed that there are nobody forces in the medium and it is initially quiescent.
Thus, the field equations in spherical one-dimensional case can be put as:
![]() (6)
(6)
and
![]() (7)
(7)
The non-Fourier heat transfer equation due to a laser heating pulse decaying exponentially in time can be written as [7] :
![]() (8)
(8)
where ![]() is the power intensity of surface reflection, I0 is laser peak power intensity,
is the power intensity of surface reflection, I0 is laser peak power intensity, ![]() is reflection coefficient,
is reflection coefficient, ![]() laser pulse parameter and
laser pulse parameter and ![]() is absorption coefficient.
is absorption coefficient.
And
![]() (9)
(9)
where![]() .
.
The constitutive equations will take the following forms
![]() (10)
(10)
![]() (11)
(11)
and
![]() (12)
(12)
where
![]() (13)
(13)
We shall use the following non-dimensional variablesfor convenience [10] :
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() (14)
(14)
where ![]() and
and![]() .
.
Equation (1) and Equations (4)-(9) assume the form (where the primes are suppressed for simplicity)
![]() (15)
(15)
By using Equation (13) into Equation (15), we get
![]() (16)
(16)
also, we have
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
and
![]() (20)
(20)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() .
.
4. The Solution in the Laplace Transform Domain
We use the Laplace transform of both sides of the last equations defined as:
![]() (21)
(21)
Hence, we obtain
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
and
![]() (27)
(27)
Eliminating ![]() between Equations (23) and (24), we have
between Equations (23) and (24), we have
![]() (28)
(28)
where![]() ,
, ![]() and
and![]() .
.
From Equations (28) and (24), we obtain
![]() (29)
(29)
From Equations (22) and (28), we have
![]() (30)
(30)
where![]() ,
, ![]() and
and![]() .
.
By eliminating ![]() between Equations (28) and (30), we obtain
between Equations (28) and (30), we obtain
![]() (31)
(31)
where![]() ,
, ![]() and
and![]() .
.
By eliminating ![]() between Equations (28) and (30), we get
between Equations (28) and (30), we get
![]() (32)
(32)
where![]() .
.
The bounded solutions of the Equations (31) and (32) take the forms
![]() (33)
(33)
and
![]() (34)
(34)
where ![]() are the roots of the equation
are the roots of the equation
![]() (35)
(35)
By using Equations (33) and (34) into Equation (30), we obtain
![]() (36)
(36)
Hence, we get
![]() (37)
(37)
To get the constants![]() , we have to apply the boundary conditions on the surface of the cavity when
, we have to apply the boundary conditions on the surface of the cavity when ![]() (R is the radius of the cavity). We will consider that the heat conduction
(R is the radius of the cavity). We will consider that the heat conduction ![]() and the strain
and the strain ![]() have zero value on the surface of the cavity, which gives that
have zero value on the surface of the cavity, which gives that
![]() (38)
(38)
Thus, the system of the equations on (34) and (37) gives the following linear equations
![]() (39)
(39)
and
![]() (40)
(40)
By solving the above system, we get
![]() and
and ![]()
Those complete the solutions as following
![]() (41)
(41)
![]() (42)
(42)
Substituting from Equations (41) and (42) in (28), (27) and (25) we get![]() ,
, ![]() and
and ![]() respectively.
respectively.
5. Numerical Inversion of the Laplace Transform
To determine the solutions in the time domain, the Riemann-sum approximation method is used to obtain the numerical results. In this method, any function in Laplace domain can be inverted to the time domain as:
![]() (43)
(43)
where Re is the real part and ![]() is imaginary number unit. For faster convergence, numerous numerical experiments have shown that the value of
is imaginary number unit. For faster convergence, numerous numerical experiments have shown that the value of ![]() satisfies the relation
satisfies the relation ![]() Tzou [9] .
Tzou [9] .
6. Numerical Results and Discussion
We now consider a numerical example for which computational results are given. For this purpose, copper is taken as the thermoelastic material for which we take the following values of the different physical constants [11] :
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
From the above values, we get the non-dimensional values of the problem as:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Figures 1-5 represent the conductive temperature distribution, the thermodynamic temperature distribution, the strain distribution, the displacement distribution, and the stress distribution respectively, in the context of one-temperature type (solid lines) and two-temperature type (dashed lines). We can notice that the two-temper- ature parameter has significant effects on all distribution. The material reaches the steady state through the two- temperature type before the one-temperature type. The peak points decrease when we use the two-temperature type.
![]()
Figure 1. The conductive temperature distribution.
![]()
Figure 2. The thermodynamic temperature distribution.
![]()
Figure 4. The displacement distribution.
Acknowledgements
I want thank Prof. Hamdy M. Youssef (Mechanics Department, Faculty of Engineering, Umm Al-Qura University, Makkah KSA) for his help and advises to me to complete this work and to choose this respected journal.