Joint Coordination Organizes to Form the Task-Dependent Trajectory of the Body Center of Mass ()
Received 20 November 2015; accepted 11 January 2016; published 14 January 2016

1. Introduction
As multi-joint movements are usually involved in whole-body motion in humans, various combinations of joint movements are used to accomplish the same purpose on different occasions. Hence, during whole-body motion, the central nervous system (CNS) needs to select one combination of joint movements from an innumerable set of combinations. Furthermore, as the goal of whole-body motion is represented by task-oriented body center of mass (COM) displacement [1] [2] , the CNS also needs to control the task-dependent COM position. Thus, the CNS needs to control, even at the kinematic level, various potential COM and joint movements. From the viewpoint that the CNS controls various mechanical degrees of freedom, Bernstein [3] addressed this problem as the degree of freedom problem in the motor control paradigm.
Solutions for the problem in which the CNS controls both COM and joint movements have been proposed in recent studies [4] - [6] . Scholz and Schöner [4] assessed the variability of variables, including the COM, head, and hand during a sit-to-stand motion at the Jacobian space (i.e., joint space), and observed that the variability of the COM was the smallest. Thus, they concluded that, among the different variables, the CNS primarily controlled the COM. Based on these findings, the authors moreover propose the uncontrolled manifold hypothesis, which states that the CNS solves the degree of freedom problem by controlling only task-dependent variables such as the COM, and does not control the joint angles. Furthermore, Scholz et al. [6] applied this hypothesis to the equilibrium of the whole body against perturbations, and found that the CNS controlled the COM as a means to maintain the equilibrium of the whole body. This finding supports the general assumption that, during whole-body motion, the CNS only controls the COM. As the CNS only appears to control the COM position and does not control joint movement, the coordinative structure among the joints must be organized to form the COM position. Moreover, considering that the COM is controlled to form a task-dependent path, the organized coordinative structure among joints should in theory display a specific or lawful shape based on a particular task. Although Scholz and colleagues [4] - [6] indicated that, during whole-body motion, each joint of the lower limb would coordinate in order to maintain a constant COM trajectory, they did not report on the shape of coordination among the joints. In fact, to our knowledge, there are no previous studies on the shape of such joint coordination, particularly for whole-body motion.
Therefore, in the present study, we select downward squatting as a task to elucidate the mutual relationship between the COM trajectory and joint movement, as well as shape of coordination among joints. Downward squatting involves a motion that lowers the COM. With regard to the mechanical equilibrium, since an individual can maintain an equilibrium without falling as his COM represents his base of support (i.e., foot length of approximately 25 cm in the sagittal plane), he can perform this motion with various COM trajectories. Moreover, the COM position is determined by the joints of the whole body. Assuming that the COM trajectory is formed by the three joints of the hip, knee, and ankle, in the case of motion in a plane, there are two coordinates of the body COM (e.g., x and y) and three joint angles. Thus, as shown in Equation (1) below, an equation to determine the COM coordinates would be an ill-posed problem because the number of COM coordinates is lower than that of the joint. Consequently, it may be redundant for combinations among the joints to determine COM coordinates. Moreover, although joint coordination during squatting is constrained by maintaining equilibrium [7] and by anatomical elements, as one segment angle (e.g., trunk angle) during the motion is altered, the other two segment angles (e.g., shank and thigh angles) can change in numerous combinations. Hence, elucidating the relationship between the COM path and joint coordination during the squatting motion with altering trunk angles can help clarify the shape of joint coordination that forms the COM trajectory, and we thus selected a downward squatting motion as the task in the present study.
Based on previous studies that the CNS controls task-dependent COM position [4] [5] and that whole body movements are constrained by maintaining equilibrium [7] , we hypothesized that the COM trajectory would show a particular one, even if segment angles are altered, and that the joint movements would show a lawful shape of coordination to form a controlled COM trajectory.
2. Methods
2.1. Subjects
Eight healthy males, aged 20 - 28 years, participated in this study. The mean (± standard deviation [SD]) height and mass of the subjects were 1.73 ± 0.04 m and 67.8 ± 7.7 kg, respectively. All subjects were student volunteers from Tohoku Bunka Gakuen University and had no history of musculoskeletal disorders. The volunteers read a description of the purpose, risks, and basic procedures of the experiments and provided informed consent prior to participation in this study. The ethics committee at Tohoku Bunka Gakuen University approved the experimental procedures in this study.
2.2. Experimental Procedure
Each subject stood barefoot, with his feet at a width of 20 cm. The subjects were instructed to squat downwards by approximately 15 cm at their preferred speed, and maintain the squatting posture for 3 s. To elucidate the relationship between the COM trajectory and joint coordination upon altering one segment angle, we set five trunk angle conditions. The trunk angle relative to a vertical line at the final position varied at 0˚ (C1), 20˚ (C2), 30˚ (C3), 50˚ (C4), and 70˚ (C5). The final posture of the trunk under each condition was visualized by two bars (like a microphone stand). Each subject practiced a few times until the motion could be performed smoothly, after which five trials were performed under each condition.
Infrared reflective markers were placed on the skin of each subject’s right shoulder (acromion), hip (great trochanter), knee (lateral femoral condyle), ankle (lateral malleolus), and foot (5 thmetatarsal bone). The movements of the markers were recorded by using a 3-D motion analysis system (Vicon 370, Vicon Peak, UK: 60 Hz). The data were smoothed by using a low pass filter at 5 Hz [8] . The segment angles were defined as the angle between the vertical line and each segment (Figure 1). The COM coordinates (X, Y) of the whole body in the sagittal plane were estimated by using the following Equation (1):
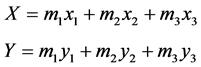 (1)
(1)
where m1, m2, and m3 represent the shank, thigh, and trunk mass relative to the whole-body mass of each subject [9] , respectively, and x1 (y1), x2 (y2), and x3 (y3) represent the x (y) coordinates of the COM of the shank, thigh, and trunk [9] , respectively. In order to determine whether there are differences in the shape of the COM trajectory between conditions, the relative anteroposterior (AP) displacement of the COM was calculated by dividing the maximum AP displacement of the COM when the subject squatted 15 cm by 15 cm, which is the minimum vertical displacement. All procedures were performed using MATLAB (Math Works Inc., MA, USA).
2.3. Statistical Analysis
Two separate repeated measure analysis of variance (ANOVA) with one within-subject factor (trunk flexion angle condition) were performed for the relative AP displacement COM and the trunk angle at the final position. Bonferroni multiple pairwise comparison was performed as a post-hoc test. The cutoff for statistical significance was set at p < 0.05. All statistical analyses were performed using SPSS software (IBM Corporation, NY, USA).
3. Results
3.1. COM Trajectory
The COM trajectories of all subjects under each condition are shown in Figure 2. The trajectories showed subject-dependent paths, and, as hypothesized, no systematic alteration upon altering the trunk angle was observed.
![]()
Figure 1. Definitions of the segment angles.
![]()
Figure 2. The averaged center of mass trajectories for all subjects (n = 8) under each condition. The origins include the start position of each subject. Each line under each condition represents one subject averaged over five trials. Each color under each condition represents one subject.
Moreover, most subjects showed roughly vertical COM paths under each condition. The relative AP displacements of the COM under all conditions are shown in Table 1. This displacement was nearly zero under all conditions, indicating that the COM trajectories were roughly vertical. Moreover, ANOVA, which was performed to examine whether there were differences in the relative AP displacements among conditions, showed no difference (p > 0.05), suggesting that the COM trajectories did not depend on the trunk conditions.
3.2. Joint Movements
The trunk angles at the final position were significantly different between conditions (p < 0.001), meaning that the subjects performed the set trunk angles in each condition (Figure 3(a)). Figure 3(b) illustrates the changes in the shank and thigh angles as a function of the trunk angle. The shank angle systematically decreased as the trunk angle increased, whereas the thigh angle remained constant. The relationship among the shank, thigh, and trunk angles in the final positions are shown in Figure 3(c) as a three-dimensional phase portrait, since the COM position in this study was determined by the segment angles of the shank, thigh, and trunk. The shank and trunk angles showed a lawful relationship―i.e., the shank angle decreased with an increase in the trunk flexion angle in the plane where the thigh angle was approximately 40˚ (gray square).
4. Discussion
4.1. Formation of COM Trajectory
We found that, based on the ANOVA results (Table 1), there was no difference in the path of the COM trajectory under all trunk conditions. Moreover, the whole-body COM trajectory during the squatting motion formed
![]()
Figure 3. (a) The mean trunk angle for all subjects under each condition. The error bars represent the standard deviation. **p < 0.001. (b) The shank (black circle) and thigh (white square) angles as a function of the trunk angle. (c) Three- dimensional phase portrait showing the relationships among the shank, thigh, and trunk angles in all subjects under all conditions. Each plot represents the average of five trials under each condition for each subject.
![]()
Table 1. Relative anteroposterior displacement (dimensionless) for all subjects under each condition.
an approximate vertical in all subjects (Figure 2). Although whole-body motions were constrained by biomechanical dynamics (i.e., postural stability and maintaining of equilibrium [7] ), individuals could maintain equilibrium without falling as long as the body COM remains within the subject’s base of support. During the squatting motion in the present study, the base of support was a foot length of approximately 25 cm in the sagittal plane. When this motion was performed within that base of support, there were innumerable COM paths that could be formed. However, in the present study, the COM showed nearly vertical paths, even though the trunk configuration while squatting varied. It was considered that this verticality of the COM trajectory mighty not only be due to the fact that whole-body motions were constrained by dynamical equilibrium, but also due to the fact that the torques of joints forming the COM trajectory were minimized. Using a quiet standing task, and while assuming that the whole body formed an inverted pendulum with a point mass positioned on the COM, Winter et al. [10] examined the relationship between the pendulum angle and the plantar flexion torque in the ankle joint; they found that the ankle plantar flexion torque increased as the pendulum angle increased. This finding indicated that, for the squatting motion in the present study, as the COM moved outside the vertical path (i.e., AP excursion), it needed excessive torque (muscle work) to control the joint movements required for adjusting the sway. In addition, Yamasaki et al. [11] compared the verticality of the COM rising path after seat-off during a sit-to-stand motion in experiments with the verticality simulated by two models (minimum jerk model and minimum torque-change model); they found that the verticality computed by the minimum torque-change model was more consistent with that in the experiment than that computed by the minimum jerk model. This finding suggested that the verticality of the COM trajectory was a form that minimized torques caused by muscles. Thus, the findings regarding the formation of the COM trajectory in the present study indicated that the COM path during whole-body motion would assume a shape that depended on the task and that minimized muscle work.
4.2. Mutual Relation between the COM and Joint Movement
The COM showed a roughly vertical trajectory under all trunk conditions, while the joint movements systematically varied among trunk conditions (Figure 3(b), Figure 3(c)). As shown in Figure 3(b), the shank inclination angle decreased as the trunk angle increased, whereas the thigh angle remained constant. The findings that the joints coordinately varied with altering trunk angles and that the COM trajectory formed task-dependent paths suggested that the joint movements were altered in an organized manner to form the COM path while ensuring that the muscle torques were minimal. Thus, these findings might indicate that the CNS controlled the COM position while minimizing muscle torque, and that joint movements were coordinately organized to form the COM position. Bernstein [2] proposed that since motions could be performed in a hierarchical structure, as individuals perform motions such as squatting or walking in a space, the muscle-joint linkage at the lower level was involved in background adjustments to obtain the goal of motion. In addition, the uncontrolled manifold hypothesis proposed by Scholz and colleagues [4] - [6] indicated that the CNS controlled the task-dependent COM position, but did not control joint movements, and that each joint in whole body motion coordinated to form a task-dependent COM position. Thus, the present findings indicated that joint movements were organized to form the COM position, all of which were controlled by the CNS.
As joint movements organize to form a task-dependent COM position, these organized joint movements should in theory have a lawful coordination dependent on the task. However, previous studies have not examined the coordination of these organized joint movements. Herein, the relationship among the segment angles, as observed in the phase portrait in Figure 3(c), indicated a lawful connection of the organized joints―i.e., the shank angle decreased as the trunk angle increased in a plane wherein the angle of the thigh was constant (approximately 40 degrees). This lawful connection suggests that each segment has a different role in squat downward. As the trunk angle is increased with constant angles of the shank and thigh, the COM moves anteriorly; this movement would result in excessive ankle joint torque [10] . The COM anterior displacement attribute to increase of the trunk angle in theory could be decreased by decrease of the shank inclination angle and increase of the thigh flexion angle. However, in the present study, only the shank angle was altered upon changes of the trunk angle, and not the thigh angle. These findings may indicate that shank movement shows a coordinating relationship with trunk movement in order to adjust AP displacement of the COM. The finding that the thigh angle remained constant as the trunk angles were altered suggests that this angle determines the depth during downward squatting. In the present study, the depth of squatting was set at approximately 15 cm (Figure 2). Therefore, all subjects performed downward squatting of 15 cm under all conditions. We believe that a thigh angle of 40 degrees is essential for squatting downwards by a depth of 15 cm. These findings are novel and suggest that
![]()
Figure 4. Schematic of the hypothesis proposed in this study. The central nervous system controls the center of mass (COM). The COM trajectory is constrained by biomechanical dynamics and minimum muscle torques, and the joints (segments) are coordinately organized while being constrained by the COM trajectory.
the joints in the whole body are coordinately organized to adjust the COM position.
The differences in the shank and thigh angles with a change in the trunk angle may be associated with a synergy at the kinematic level. Latash et al. [12] stated that lawful changes during multi-joint movements can arise only when each element (joint angle) of the system is coordinately organized in synergy, and not when it is independently controlled by the CNS. Furthermore, Rosenbaum [13] described that multi-joint movements that occur with ease, such as rotation of the elbow and wrist joints in the same direction, are movements occurring with synergy, whereas those that occur without ease, such as rotation of the elbow and wrist joints in opposite directions, are movements occurring without synergy. In the present study, the trunk and shank rotated around the hip and ankle joints, respectively, in a clockwise direction, while the thigh rotated around the knee joint in a counter-clockwise direction. This finding suggests that the coordinative connection between the trunk and shank results from synergy. Moreover, the finding that this coordination arises in a plane with a thigh angle of approximately 40 degrees suggests that the thigh movement compensates for the coordinative connection. Further studies are needed to confirm this hypothesis.
In summary, the present study indicated that the coordination of whole-body segments would be organized in a lawful manner to form the task-dependent COM trajectory. Furthermore, the present study suggested the following: 1) the CNS controls only the COM position and not the joint movement; 2) the COM is constrained not only by biomechanical dynamics (i.e., maintaining equilibrium and postural stability) but also by minimum muscle torques and; 3) the segment movements, which constitute the joint movement, consist of coordination with synergy between the trunk and shank, and of the thigh movement that compensates for the coordination; this has been represented as a schematic in Figure 4.