Triangle Method for Estimating Soil Surface Wetness from Satellite Imagery in Allahabad District, Uttar Pradesh, India ()
Received 2 December 2015; accepted 10 January 2016; published 13 January 2016

1. Introduction
The demand for spatially distributed land surface information such as soil surface wetness in agriculture, hydrology and environmental engineering is now increasing exponentially than before [1] . Soil surface wetness influences the interactions between the land surface and atmospheric processes such as partitioning of energy into sensible and latent heat fluxes [2] .
Soil moisture is highly variable in space and time; therefore point based measurements are difficult, cumbersome to obtain over wide area [3] . Remote sensing as geospatial technology has excellent capabilities to infer moisture availability (soil surface wetness) over a target at a specific time. Therefore, soil surface wetness can be mapped so as to give adequate information for certain users in agriculture and hydrology [4] .
The retrieval of soil moisture from satellite measurements has been the special interest for many researchers from 1978 hitherto (the launching date of SAR system with Seasat). Microwave portion of the electromagnetic spectrum is first proved to be successful for retrieval of soil moisture and vegetation parameters [1] . Other techniques such as Optical/TIR (triangle method), thermal inertia, gamma radiation and hyperspectral have been proposed and successfully carried out for inferring soil surface wetness from satellite data [3] [5] .
The Triangle Method for estimating land surface moisture and energy fluxes emerged in 1990’s [6] . The method uses the relationship between scaled surface radiant temperature and fractional vegetation cover derived from remotely sensed data. The underlying principle of this method is that surface radiant temperature is sensitively dependent upon soil surface wetness. Hence, spatial and temporal variations in surface wetness are reflected by variations in surface radiant temperature.
The merits of remote sensing techniques for monitoring surface soil moisture over the traditional means include: synoptic, timely coverage with good repeat passes (temporal resolution) and efficiencies of scales [7] . Specifically, the great importance of the triangle method is that it does not need ancillary atmospheric and surface data [6] . This paper is aimed at using the Triangle Method to estimate soil surface wetness in Allahabad district of Uttar Pradesh, India.
2. Materials and Methodology
2.1. Materials
2.1.1. Study Area
This study was conducted in Allahabad district. Allahabad district is enclosed between latitude 25.45˚N and longitude 81.84˚ at an elevation of 98 meters (322 ft) above mean sea level [8] . The district is situated in the southern part of the Uttar Pradesh, India. Six (6) Tehsils (geographical areas) were chosen for the study. These are Karchhana, Phulpur, Bara, Koraon, Soraon and Handia (Figure 1). Chaka Block (sub-study area) which is situated within the Karchhana Tehsil was selected as soil sampling site (Figure 1).
The typical climate of Allahabad is humid subtropical climate denoted as Cwa in the Köppen climate classification. This type of climate is common to cities in north-central India. The annual rain is about 1027 mm. The temperature ranges from 40˚C to 45˚C and from 2˚C to 24˚C during summer and winter respectively [8] [9] .
The soils of Allahabad district were developed under the synergistic impacts of a wide range of soil forming factors including climate, vegetation and parent materials. The area is covered by layers of alluvium spread by the slow-moving rivers of the Ganges system [10] . Alluvial soils are the most fertile soils among all Indian soils
![]()
Figure 1. Study area and sampling points.
[11] . Chaka block has moderately shallow and eroded loamy soils [12] . The vegetation of the study site consists mainly of scrub. Forests lie in Trans-Yamuna and some portions of the Vindhya Hills.
2.1.2. Dataset Description
This study made use of Landsat 7 Enhanced Thematic Mapper Plus data. The ETM+ sensor onboard Landsat 7 image consists of 8 spectral bands (blue, green, red, near-infrared, shortwave infrared, thermal infrared and panchromatic).
Landsat 7 ETM+ data (Path/Row 143/42) was procured from United States Geological Survey (USGS) site (http://glovis.usgs.gov). The acquisition dates of the images are 30th January, 2015; 15th February, 2015; 19th March, 2015; 20th April, 2015 and 6th May, 2015. The images of 3rd March, 2015 and 4th April were very cloudy.
2.1.3. In Situ Measurements
Soil samples were collected at some locations (22 sampling points) in Chaka Development Block area at two depths (0 - 5 cm and 5 - 15 cm). The Landsat 7 ETM+ overpass time is 5:00 am GMT which corresponds to 10:30 am Indian time. Therefore, soil sampling was carried out between 10:30 and 11:30 am (local time of India). Gravimetric method was used to determine the moisture content using procedures explained in [11] .
2.2. Methodology
2.2.1. Data Pre-Processing
The brightness values (DNs) were converted to radiance (W m−2 sr−1 μm−1) using the radiometric calibration coefficients of Landsat 7 ETM+ according to [13] procedure.
 (1)
(1)
where:


Lλ = Spectral radiance at the sensor’s aperture [W/(m2 sr μm)]; Qcal = Quantized calibrated pixel value [DN]; Grescale = Band-specific rescaling gain factor [(W/(m2 sr μm))/DN]; Brescale = Band-specific rescaling bias factor [W/(m2 sr μm)].
The at-satellite band reflectance (BD) was computed from at satellite directional radiance as follows: [13] [14] .
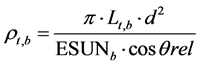 (2)
(2)
where:  is at-satellite band reflectance (BD)/Planetary TOA reflectance [unitless]; π is mathematical constant equal to ~3.14159 [unitless];
is at-satellite band reflectance (BD)/Planetary TOA reflectance [unitless]; π is mathematical constant equal to ~3.14159 [unitless];  is at-satellite spectral radiance in band b (W m−2 sr−1 μm−1); ESUNb is the mean solar exoatmospheric radiation over band b (W m−2 sr−1 μm−1); θrel is solar incident angle or solar zenith angle relative to the land surface slope and d2 is earth-sun distance in astronomical unit. The parameter d2 is computed as the function of day of year using the following equation: [13] [14] .
is at-satellite spectral radiance in band b (W m−2 sr−1 μm−1); ESUNb is the mean solar exoatmospheric radiation over band b (W m−2 sr−1 μm−1); θrel is solar incident angle or solar zenith angle relative to the land surface slope and d2 is earth-sun distance in astronomical unit. The parameter d2 is computed as the function of day of year using the following equation: [13] [14] .
 (3)
(3)
where DOY is day of year and 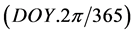 (rad).
(rad).
2.2.2. Derivation of Normalized Difference Vegetation Index (NDVI) and Fractional Vegetation Cover
NDVI which is a function of the surface derived reflectance in the Red and NIR bands was calculated using the following formula:
 (4)
(4)
where:  is reflectance in the near-infrared band;
is reflectance in the near-infrared band;  is reflectance in the red band.
is reflectance in the red band.
Fractional vegetation cover was derived from the scaled NDVI (N*).
 (5)
(5)
where N* is calculated using the following formula as:
 (6)
(6)
NDVI0 is the value corresponding to bare soil and NDVImax is the value corresponding to the full vegetation [15] .
2.2.3. Derivation of Emissivity Corrected Surface Radiant Temperature
The surface emissivity can be incorporated into thermal atmospheric correction of thermal remotely sensed data so as to determine accurate radiometric temperatures [15] . Therefore, surface emissivity was computed so as to incorporate it into land surface temperature derivation algorithm.
 (7)
(7)
where: T is in degrees Kelvin. It can be converted to degree Celsius by subtracting 273.15 from the Kelvin values.
K1 and K2 are calibration constants for Landsat 7 ETM+ equal to 666.09 W m−2 sr−1 μm−1 and 1282.71 W m−2 sr−1 μm−1 respectively [13] [16] .
CVRI is cell value as radiance (W m−2 sr−1 μm−1); ε is surface emissivity [unitless] computed using Equation (8).
![]() (8)
(8)
where: Fr is fractional vegetation cover; ![]() is pixel’s emissivity;
is pixel’s emissivity; ![]() is emissivity of vegetation;
is emissivity of vegetation; ![]() is emissivity of soil.
is emissivity of soil.
2.2.4. Scaling NDVI and Surface Radiant Temperature
The NDVI was scaled using the formula discussed above in Equation (6). Surface radiant temperature was also scaled likewise according to [6] algorithm.
![]() (9)
(9)
where: Tir is surface radiant temperature; Tmin is minimum temperature in the image; Tmax is maximum temperature in the image. Both the N* and T* values range from 0 to 1.
2.2.5. Creation of T*-Fr Triangular Space
A scatter plot of Fr versus scaled surface radiant temperature was developed for each date in order to observe the triangle. The Fr was plotted on ordinate while the scaled surface radiant temperature on abscissa. An algorithm was used to fit the warm edge according to [2] procedure.
![]() (10)
(10)
where: Fri is the fractional vegetation cover of pixel i-th pixel; a is the intercept of the linear warm edge; b is the slope of the linear warm edge.
2.2.6. Transformation of Pixel Measurements into Soil Surface Wetness
Pixel measurements were transformed into soil surface wetness (moisture availability) using 3rd order polynomial equation developed by [6] from the output of Soil Vegetation Atmosphere Transfer Model (SVAT). The inputs of this polynomial algorithm are fractional vegetation cover, scaled surface radiant temperature and coefficients.
![]() (11)
(11)
where: Mo is moisture availability (soil surface wetness) at a pixel; T* is pixel’s scaled surface radiant temperature; Fr is pixel’s fractional vegetation cover; aij is coefficient of the equation.
3. Results and Discussion
3.1. T*-Fr Scatter Plot
The scatter plot of the T* versus Fr resembles a triangle in each date under study (Figure 2). Fr was plotted on the ordinate while the scaled surface radiant temperature on the abscissa. The emergence of the triangular space
![]()
Figure 2. Triangular space of scaled surface radiant temperature versus fractional vegetation cover (before removal of standing water pixels).
is an indication of the presence of wide range of soil surface wetness within the area under investigation. These findings are in accord with the interpretation of triangular space by [6] [17] [18] .
The moisture availability (soil surface wetness) varies linearly from the warm edge (Mo equals to zero) to the cold edge (Mo equals to 1). The warm edge is the right edge of the distribution and it represents the pixels with warm surface temperature. The higher surface radiant temperature along this edge is either as a result of low evaporation rates from dry soils under low vegetation condition or low transpiration rates from vegetation canopy under high ground vegetation cover (owing to the low soil moisture) which in turn causes stomatal closure in the canopy. The left edge is defined as the cold edge. Pixels along this edge have cool surface temperature. This is because of high evaporation rates from wet soils under low vegetation condition or high transpiration from vegetation canopy under high vegetation condition which indicates the presence of high amount of moisture and lack of water stress.
The cloud and water pixels distort the shape of the triangle around the boundaries. It is very noticeable in the triangles of the 30th January, 2015 (DOY 30), 15th February, 2015 (DOY46) and 19th March, 2015 (DOY 78) that the triangles bulge in the lower left side. This distortion is likely to be caused by standing water pixels because of lower reflectivity and a bit higher temperature of water in comparison with cloud. Figure 3 depicts the results of standing water pixels’ distortions removal on 30th January, 2015, 15th February, 2015, and 19th March, 2015).
![]()
Figure 3. Triangular space of scaled surface radiant temperature versus fractional vegetation cover (After removal of standing water pixels).
3.2. Spatial and Temporal Distribution of Soil Surface Wetness
Soil surface wetness tends to vary spatially and temporally owing to the certain factors such as the nature of the scenery, soil type, land use et cetera. Chaka block in Allahabad was chosen to show the spatial variation of simulated soil surface wetness. The findings have shown that soil surface wetness varied spatially and temporally within the area under investigation. Figure 4 depicts the spatial variability maps of simulated soil surface wetness
![]()
Figure 4. Spatial distribution of simulated soil surface wetness in Chaka block.
![]()
Table 1. Correlation coefficient (R2) between simulated soil surface wetness and ground measured volumetric water in Chaka block.
at 30 m resolution using third order polynomial algorithm on the study dates. The range of soil surface wetness decreases progressively between DOY 46 and DOY 110. This might be as a result of the absolute cessation of rainfall between March and April.
3.3. Correlation Analysis
The simulated soil surface wetness using the 3rd order polynomial algorithm was correlated with ground measured volumetric soil moisture at depths 0 - 5 cm and 15 cm. The findings showed a very weak correlation between the simulated soil surface wetness and ground measured soil moisture at deeper soil layers (Table 1). This indicated that triangle method can only estimate soil surface wetness at superficial layer of the soil (0.5 to 1 cm). This should be taken into consideration when the method is being applied.
The weak correlation between the simulated and measured soil moisture (soil surface wetness) can be attributed to the depth at which soil moisture measurements were made. To find out the possible reason(s) for the weak correlation between simulated and estimated soil moisture in the present study, series of personal communications were made with the developer of the algorithm [19] in May, 2015 (Professor Toby N. Carlson, Penn State University, USA). According to [19] it might be difficult to get a good correlation between ground measured volumetric soil surface moisture at deeper substrate and estimated soil surface wetness using triangle method, as the latter technique estimates moisture availability (soil surface wetness) at the top skin layer of the soil (0.5 to 1 cm). This is because the drying rates at the surface discontinue to be linearly correlated to that at lower levels (depths) during the satellite overpass.
4. Conclusion
This study demonstrated the efficient remote sensing techniques for estimating soil surface wetness (surface moisture availability) using a relationship between scaled surface radiant temperature and fractional vegetation cover on the triangular space (triangle method). The simulated soil surface wetness and ground measured soil moisture did not correlate well. The possible reason of poor correlation between simulated and measured soil moisture could be attributed to the depth at which soil moisture measurements were made. In this regard, triangle method had capability of estimating soil moisture at the superficial soil layer (0.5 - 1 cm).
Acknowledgements
The authors would like to express their gratitude to Professor Emeritus Toby Nahum Carlson of Penn State University, USA for his precious advice and help.