Validation of a Statistical Forecast Model for Zonda Wind in West Argentina Based on the Vertical Atmospheric Structure ()
Received 17 November 2015; accepted 8 January 2016; published 11 January 2016

1. Introduction
Zonda is a strong, warm, very dry wind associated with adiabatic compression upon descending the eastern slopes of the Andes Cordillera in western-central Argentina (Figure 1), with a higher frequency in the winter and spring seasons. Zonda has specific features (such as remarkable spatial and temporal variability), and complex behavior of associated meteorological parameters (such as temperature, relative humidity, surface pressure, and wind intensity). In populated regions, it produces a range of damage according to the intensity of wind gusts (e.g. blowing off roofs, felling trees and high-voltage power lines, and interrupting power supply and communication services). In addition, it favors the ignition and propagation of fires and causes damage to crops due to the strong gusts, sudden dryness and high temperatures, and it may also be responsible for premature fruit flowering. At high altitudes in the mountains, its occurrence accelerates snow melting and evaporation, modifying the snow pack depth, contributing to avalanches, and influencing the hydrological cycle.
Initial investigations into this kind of wind focused on the Alpine region, where it is known as the “foehn”. This term became the generic name for all descending, warm, dry winds whose features and effects depend on topography, its interaction with the atmospheric flux, and the particular meteorological conditions. Such winds have different names depending on where they blow: “Chinook” in the USA and Canada east of the Rocky Mountains, “Canterbury-northwestern” in New Zealand, “berg wind” in South Africa, “afganet” in Central Asia, “ibe” in western China, “halnywiatr” in Poland and Slovakia, and “austru” in western Romania [1] -[4] .
The history of zonda research in Argentina, its climatology and the forecasting problems are well explained in [1] , where there is reference to a probabilistic method and the predictors obtained.
The main goal of this paper is to validate the accuracy or skill of a statistical forecast, developed by Norte [1] [2] , for zonda wind based on the behavior of the vertical structure of the atmosphere.
![]()
Figure 1. Location of Mendoza and San Juan provinces in Argentina, South America.
The model made use of the Stepwise Discriminant Analysis (SDA). Thanks to the positive results obtained for predicting zonda wind [2] , this statistical tool was later also applied in: [5] to compare zonda wind and snowfall prediction, [6] to predict frost using only surface data, [7] to predict frost using the vertical profile of the atmosphere, [8] to predict cyclogenesis development in the Río de la Plata estuary and surroundings, [9] to predict late frost in a particular valley (San Rafael), and [10] to build a statistical model for predicting convection.
Three sets of Probabilistic Predictors were obtained by Norte [1] [2] :
・ One set was obtained analyzing the 12 UTC pressure spatial gradient where some zonal and meridional pressure differences were arbitrarily defined.
・ Another analysis was conducted taking the 12 UTC pressure values (reduced to sea level) of 81 surface meteorological stations, to obtain only the ones that would best discriminate among groups. SDA selected only five stations from the total set.
・ Finally, a third set of predictors was obtained from Quintero (Chile) rawinsonde data.
These Probabilistic Predictors are not analyzed in this paper. For more information, it can be seen in [1] [2] .
The secondary goal of this paper is to describe the climatology of the vertical profile leeward of the Andes Cordillera for the period considered when the forecast model was created. The data analyzed in [2] were used as reference.
This paper is structured in four sections and two appendices. Following this Introduction, Section 2 describes the data and methodology. Section 3 includes the results obtained with the prediction program, and the rawinsonde climatology showing the vertical structure of the atmosphere leeward of the Andes Cordillera. Section 4 presents the discussion and conclusions about the prediction model. Finally, the different statistical tools used in this paper are explained in Appendices A and B.
The relevance of the present work is twofold: not only does it validate the effectiveness of a prediction method based on rawinsonde data, but it is also a valuable tool both for forecasters and decision-makers considering that the analyzed region is protected by laws for zonda risks prevention, especially when the phenomenon can be severe or extreme. Thus, the main contribution of this paper is that, by validating the prediction model, it ensures the use of one more tool for forecasters. Additionally, improving the accuracy in zonda wind forecasts will be of aid when making decisions to ameliorate its impact.
2. Data and Methodology
The statistical forecast of zonda wind based on the behavior of the vertical structure of the atmosphere was built for the months of May, June, July and August of the 1974/1983 period. It was verified against a series of cases recorded in the Mendoza Aero and San Juan Aero weather stations for those same months of the 2005/2014 period.
Rawinsonde data from Mendoza Aero station were scarce or non-existent for the validation period, and simulated rawinsonde data produced by the ARL (Air Resource Laboratory) from the NOAA (National Oceanic and Atmospheric Administration, Department of Commerce, USA) were used.
Zonda wind forecast with computational methods employed the Stepwise Discriminant Analysis (SDA) (see Appendix A) and four groups were defined:
・ Zonda group: days with zonda on the plains (Mendoza Aero and/or San Juan Aero);
・ Previous 24 hour group: the day preceding a zonda day;
・ Previous 48 hour group: the day preceding that defined as the “previous 24 hours”;
・ Others group: the rest of the series, i.e. days that do not belong to any of the groups mentioned above.
The days or records where categories overlapped were omitted from the sample (e.g. it could happen that a day belonging to the previous 48 hour group also belonged to the zonda group).
Once these groups were selected, it was necessary to know if any of the variables indicated unequivocally when a certain day belonged to one particular group. The variables that were thus classified would be assumed as predictors, and conditions would be met to forecast the zonda event 48 hours in advance. The SDA program made the discrimination.
Rawinsonde data from Mendoza Aero were used as predictors, with the following as input variables: surface pressure, temperature, dew point, and the zonal and meridional components of the wind on surface and of the fixed levels including up to the 200 hPa layer.
As mentioned in Appendix A, the chosen variables that discriminate best among groups are expressed as classification functions with their coefficients and constant terms, and the amount of functions is equal to the amount of groups. Each function permits to obtain a classification score on a determined day for that group, and the day will belong to the group whose function gets the highest score. In addition, the probability of a determined day belonging to one group or another can be obtained through the classification scores. The conversion formula of classification scores into posterior probabilities is shown in Appendix A.
This is how the SDA program re-evaluated the 1974/83 series, from where the case-by-case classification functions had been obtained, and this was used to evaluate the method.
As the four groups were defined with a temporal criterion, and there were variables that discriminate among those groups, it is then possible to forecast a zonda wind day.
With the discriminant functions obtained, it was possible to implement the prediction program.
Forecasts were verified evaluating the series with the discriminant functions. With the classification matrix from Table 1 and the probability used to express each forecast, they can be evaluated as deterministic or probabilistic.
The classification matrix includes information on the number of cases assigned correctly to each group. Rows correspond to observations, columns to forecasts, and the trace to the events classified correctly.
Probabilistic forecasts can be evaluated through a contingency table, and although this is not a verification method in itself, its components provide a basis for determining scores and indexes easily.
A forecast is useful when the success percentage is higher than the probability of occurrence or non-occur- rence.
The “skill score” combines the information of the contingency table to obtain the relation between the number of correct forecasts, the total number of forecasts, and the expected number of correct forecasts based on a method such as chance, persistence or climatology. Skill score is 1 when all forecasts are correct, and 0 when the correct forecasts are given solely by climatological chance.
For deterministic forecasting of zonda wind: the prediction program expresses forecasts in terms of probabilities. There is always a certain probability of zonda today, zonda tomorrow, zonda the day after tomorrow, or no zonda. The summation of these four probabilities is 1. It may happen that these groups are equiprobable or not. As the probability of one group increases towards 1 (diminishing the probability of the others), it is said deterministically that the phenomenon will occur.
For example, with results as those for the dates listed in Table 2 applied to 12 UTC data, it is deterministically forecasted YES to zonda today and the other groups are assigned NO.
This criterion was applied, day by day, to the winters of the years 1974 to 1983, and also to the 2005/2014 period. Forecasts were evaluated for each day, and the occurrence or non-occurrence of the forecasted event was verified and rated after the following classification:
・ If the forecast is YES and the observed is YES then there is a HIT.
・ If the forecast is YES and the observed is NO then there is a MISS or a FALSE ALARM.
・ If the forecast is NO and the observed is YES then there is a MISS or a SURPRISE.
・ If the forecast is NO and the observed is NO then there is a HIT.
Also, the percentage of success “A” and the “degree of success” (or “skill score” [11] ) were determined. The calculations for these percentages are explained in Appendix B.
![]()
Table 1. Classification matrix of cases using rawinsonde data at 12 UTC from Mendoza Aero, 1974/83.
![]()
Table 2. Posterior probabilities for some zonda events between 1983 and 2015.
For verifying probabilistic forecasts, the methods of Cardazzo et al. [12] were followed. The Brier score (BR) [13] was used to assess the quality of a probabilistic forecast (Equation (1)), and the Brier Skill score (BSS) to compare the BR value obtained for the forecast against the BR value of the climatology (Equation (2)), which gives some idea of how much more information the forecast provides in relation to a reference (i.e. the climatology).
The BSS can be interpreted as the distance from the probabilistic forecast of the ensemble to a perfect probabilistic forecast (i.e. the forecast predicting a 100% probability when the phenomenon occurs, and 0% when it does not).
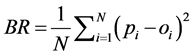 (1)
(1)
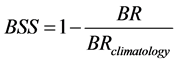 . (2)
. (2)
For probabilistic forecasting of zonda: the developed prediction programs calculate, for each day, the probability of zonda occurring today, tomorrow, the day after tomorrow or not occurring, according to the discriminant function obtained. The phenomenon can occur m times with a given probability xi stated n times. The relative frequency yi of a probability xi is the value obtained from dividing the times the phenomenon was observed (m) by the times it was forecasted (n) with a given probability xi (see Appendix B).
Besides, the climatology of the vertical profile of the atmosphere leeward of the Andes Cordillera was built with daily rawinsonde data from Mendoza Aero station for the same months of the same 1974/1983 period.
Calculations included:
1) The mean rawinsonde values belonging to the groups of days with surface zonda (i.e. wind blowing in the plains), days with high zonda (i.e. wind blowing at height) [1] [2] and total days (including surface zonda, high zonda and remaining days). In particular for Mendoza Aero, the conditions for absence of high and surface zonda were analyzed, defining this group as “no-zonda day”.
2) The anomalies of different thermodynamic parameters across groups and across locations for each group.
3) The vertical variance curves of values from Student’s t-test for validating the significance of the parameters according to levels and to groups.
4) The mean vertical profiles of the zonal and meridional wind component.
3. Results
3.1. The Prediction Program
The input data corresponded to the surface pressure values, plus the temperature and dew point values, and the zonal and meridional components of wind on surface, and the fixed levels including up to 200 hPa.
From the 53 variables considered, SDA only selected four as relevant to discriminate and to act as predictors: surface pressure, dew point depression at 850 hPa, meridional wind component at the same level, and zonal wind component at 400 hPa.
Surface pressure was selected as a relevant variable because it decreases when zonda occurs in the plains. Dew point depression at 850 hPa is important because the maximum dryness and heating due to zonda are usually recorded at that level; moreover, in the morning of zonda days in the plains, zonda may already be blowing at that height without having reached the surface (see Table 3).
A north component higher than the average at lower layers was observed in the analysis of synoptic and aerological conditions connected to zonda (see [2] , Chapter 4), which would explain why the meridional wind component at 850 hPa was selected. Also, the higher west component above the summits of the Andes, associated with the closeness of the jet stream on zonda days, accounts for its importance at the 400 hPa level.
From the results obtained for the 1974/83 period, contingency tables were built:
In addition, Table 4 shows that the hits of the (ab)-type (NO forecasted/NO observed) include the cases OTHERS forecasted/OTHERS observed, OTHERS forecasted/PREV24 observed, and OTHERS forecasted/ PREV48 observed, i.e. the remaining days when ZONDA was neither forecasted nor observed. These cases count as “hits” regarding the forecast and observation of zonda.
This criterion may raise doubts, which is why another contingency table (Table 5) was built based on the discrimination, between Zonda and Others, of variables derived from Mendoza Aero rawinsonde data (but using only two groups). It can be noted that this table and the values for A, L and S do not differ significantly from those obtained with four groups.
![]()
Table 3. Selection of predictor variables using rawinsonde data from Mendoza Aero, 1974/83.
![]()
Table 4. Contingency table for 1974/83 using the four groups.
where A = 92%, L = 112, and S = 0.90 (see Appendix B).
![]()
Table 5. Contingency table for 1974/83 using only two groups.
where A = 89%, L = 130.72, and S = 0.87.
Considering the little difference observed in the validation, and the fact that using all the groups allows inferring possible conditions up to two days in advance, it is clear that it is more advantageous to forecast using the four groups than with just two.
As regards the results obtained for the 2005/2014 validation period, different probability thresholds were tested, starting from threshold 0.60 to 0.75 (see Table 6 to Table 9).
The values listed in these tables were taken from the classification matrices calculated by SDA. The number of times zonda was forecasted but did not occur (false alarms) is much higher than the number of times Zonda was not forecasted but did occur (surprises). Using Equations (1) and (2) from Data and Methodology, the following BSS values were obtained for the different thresholds (Table 10).
In other prediction models used by Norte [1] [2] , not developed in this paper, the success probabilities show a normal distribution; however, in the method described here for the current study, the frequency of probabilities increase towards total success (see Figure 2).
![]()
Table 6. Contingency table for the 2005/14 period with threshold = 0.60.
where A = 87.3%, and S = 1.13.
![]()
Table 7. Contingency table for the 2005/14 period with threshold = 0.65.
where A = 86.7%, and S = 1.13.
![]()
Table 8. Contingency table for the 2005/14 period with threshold = 0.70.
where A = 88.4%, and S = 1.15.
![]()
Table 9. Contingency table for the 2005/14 period with threshold = 0.75.
where A = 87.3%, and S = 1.18.
![]()
Table 10. BSS values for the different thresholds.
![]()
Figure 2. Frequency of zonda probability for the 1974/83 period.
3.2. Vertical Structure of the Atmosphere Leeward of the Andes Cordillera: Rawinsonde Climatology
Table 11, Table 12 and Table 13 were built with data of May, June, July and August of the 1974/1983 period from Mendoza Aero, and they show, respectively: mean rawinsonde values for the total of days without zonda, mean radiosonde values for the days with zonda in the plains, and the anomalies of some parameters as mentioned in [2] (Chapter 4).
The abbreviations in the following tables mean: p (atmospheric pressure), h (height), T (temperature), σT (standard deviation of temperature), Td (dewpoint temperature), σTd (standard deviation of dewpoint temperature), T-Td (dew point depression), σT-Td (standard deviation of dew point depression), θ (potential temperature), θe (equivalent potential temperature), RH (relative humidity), u (zonal wind component), v (meridional wind component).
Table 13, of anomalies, shows that:
1) Height anomalies are negative up to 200 hPa, and they decrease quite steadily towards the upper troposphere, indicating the proximity of a trough (since, after the passage of an anticyclone, the trend is negative at first on the surface and then it extends to the upper levels).
2) Temperature anomalies are positive in the entire atmosphere with a maximum at around 800 hPa due to the air descent that affected those levels. From 800 hPa to 600 hPa there is a notable increase of the vertical gradient due to the effect of zonda.
3) Humidity anomalies indicate that ΔTd values are slightly positive at very low levels, with a negative maximum at 800 hPa but turning positive again at approximately 650 hPa. Dew point depression and relative humidity anomalies are more telling, indicating that the lower troposphere is drier than normal. From these, together with the temperature and equivalent potential temperature anomalies, it can be observed that zonda usually occurs with an air mass warmer than normal, and that its effect on humidity reaches a maximum at 800 hPa.
4) Wind anomalies indicate that, except at the lower levels (which zonda has not yet reached at the time of sounding), the zonal component (u) is higher than its climatological value, with a marked increase of the vertical shear between 1500 and 3300 masl and a slight increase in the upper troposphere. Regarding the meridional
![]()
Table 11. Mean rawinsonde values from Mendoza Aero for the total of days (May to August 1974/83).
![]()
Table 12. Mean rawinsonde values from Mendoza Aero for surface zonda days (May to August 1974/83).
![]()
Table 13. Anomalies (Δ) of some parameters from Mendoza Aero (zondadays group minus total days group).
component (v), although its climatological value is almost null, there is a north component in zonda events, especially between 1500 to 5500 masl, from which it decreases once again. At 5500 masl, mean climatological wind (V) corresponds to 271 or to 11 m/s, while mean wind associated to zonda at that height is 282 or 17 m/s, confirming that the wind increases when there is zonda at the height of the Andean summits (Figure 3).
Although the maximum heating produced by zonda occurs on the surface [2] (Chapter 2), soundings fail to show this. This difference could be due to the launching time of the rawinsonde weather balloon (12 UTC or 9 AM local time).
Zonda climatology [1] shows that zonda starts early in the morning in a few opportunities, but the highest onset frequency is during afternoon hours.
Also, mean rawinsonde values corresponding to the days of the series when zonda did not occur either at height or in the plains, defined as “no-zonda days”, were calculated for Mendoza Aero (Table 14).
In this case, the mean sounding values that show colder and more humid air conditions in almost the entire vertical column would be associated preferentially to polar air situations.
Figure 4 shows the vertical variations of Student’s t-test values (significant at 5% if t > 1.965) for the zonda days group against the total days group. The fact that the most important differences in temperature and dew point depression are found at 800 hPa and not on the surface would be due to the causes already mentioned regarding the time when the rawinsonde data is recorded and the onset time of zonda in the plains. The differences lose significance below the mean height of the Andean summits. As for dew point, it reaches significant values
![]()
Figure 3. Mean vertical distribution of wind in Men- doza Aero at 12 UTC from May to August 1974/83.
![]()
Figure 4. Vertical variation of student’s t-test values for zonda days group against total days group.
only at 800 hPa. The fact that the values are not statistically significant at the lower levels close to the ground (900 hPa) would indicate that the subsidence inversion is almost permanent in Mendoza Aero, at least during the winter periods.
Figure 5 shows significant differences in the entire air column, except in the surface, and allows inferring that the conditions for no-zonda days at any level are not the norm in the region during the analyzed months. The maximum values found between 800 and 700 hPa would be due to the predominance at those layers of colder and more humid air that is observed in these circumstances, in contrast with the heating and dryness produced above the inversion that can be recorded in cases of zonda occurrence.
4. Conclusions
Zonda wind occurrence markedly influences the structure of the atmosphere leeward of the Andes Cordillera in western-central Argentina.
Its maximum impact regarding temperature and dew point depression occurs at the 850 to 800 hPa levels, with significant heating and decrease of humidity.
Zonda occurs within a relatively warm air mass, with temperature anomalies being positive along the entire column. The layers affected by zonda show a notable north component in the circulation.
![]()
Table 14. Mean rawinsonde values from Mendoza Aero for no-zonda days (May to August 1974/83).
![]()
Figure 5. Vertical variation of student’s t-test values for no-zonda days group against total days group.
Surface pressure was selected as a relevant variable because it decreases when zonda occurs in the plains. Dew point depression at 850 hPa is important because the maximum dryness and heating due to zonda are usually recorded at that level; moreover, in the morning of zonda days in the plains, zonda may already be blowing at that height without having reached the surface. A north component higher than the average at lower layers was observed in the analysis of synoptic and aerological conditions connected to zonda [2] (Chapter 4), which would explain why the meridional wind component at 850 hPa was selected. Also, the higher west component above the Andean summits, associated with the closeness of the jet stream on zonda days, accounts for its importance at the 400 hPa level.
The validation of the implemented prediction program considered deterministic and probabilistic forecasts, and was highly successful. Contingency tables show that the program generally overestimates the probability of zonda occurrence in the plains, and false alarm cases are far more frequent than surprise events. All in all, the prediction program is considered to be a quite effective tool.
For this region of Argentina, it is valid what Richner and Hächler [15] state for the Alps: “In practice, the skills of experienced forecasters who are familiar with the local situations are still an indispensable prerequisite for a successful forecast! They know from experience how a somewhat different wind direction might influence the onset or breakdown of foehn in a given valley, how observed wind data must be interpreted to arrive at a correct prediction. On the other hand, any tool, be it based on probability or on model output, is a welcome and appreciated support giving a first approximation which is subsequently modulated with the forecaster’s experience and skill.” The synoptic chart, particularly the surface pressure pattern, is one of the most useful tools for predicting the onset of foehn.
The main contribution of this research is precisely that, by validating the prediction model, it ensures the support of one more tool for forecasters. In addition, improving the accuracy in zonda, wind forecasts will be of great aid for decision-makers when taking steps to ameliorate its impact.
Acknowledgements
The author wishes to thank to Rafael Bottero for his help with figures and photos, and to Claudia Bottero for formatting and proofreading.
This paper has been funded by PIP 1120090100439 of CONICET (National Research Council of Argentina).
Appendix A: The Stepwise Discriminant Analysis (SDA) Program
The program applied in this paper to discriminate between zonda days and no-zonda days, and to obtain a system for forecasting the phenomenon, can also generate a discriminant analysis between two or more groups of parameters.
The variables used to calculate the linear classification functions are chosen step by step, hence stepwise. At each step the variable that adds the most to the discrimination between groups is entered into (or the variable that adds the least is removed from) the discriminant function.
The output shows, in the first place, a list of the variables to be entered. Then, it indicates the specific options of the program, many of them pre-assigned, such as Fisher’s F-statistics [14] ―which is the minimum required for the variable to be entered in or removed from the discriminant function, the maximum amount of steps it accepts and the prior probabilities of each group.
Then, the program informs the number of cases read. A characteristic of this program is that it uses only complete cases. This means that if the value of any variable in a case is missing or out of range, the case is omitted from all computations. The program informs the number of omitted cases and of the remaining cases which are used to carry out the stepwise discrimination.
Next, the program estimates the mean values, standard deviations and variation coefficients for each variable in each group and for all groups.
Standard deviation within groups is:
![]() ,
,
where Σ identifies the summation, ![]() is the variance and Nk the sample size of the kth group.
is the variance and Nk the sample size of the kth group.
Step 0 corresponds to the step before any variable is entered into the discriminant function.
The program prints the F-statistic “to enter” for each variable considered. F was computed from a one-way analysis of variance on the variables of the groups used in the analysis, which allowed establishing the degree of likeness or difference between each group for each variable.
The variable with the highest F-to-enter at step 0 is entered into the discriminant functions. This is the variable that discriminates the best between groups.
Step 1 computes the following:
1) F-to-remove for the variable in the equation.
2) F-to-enter for each variable not in the equation, which is equal to the F-statistic from the one-way variance analysis of the residual variables.
3) Wilk’s lambda or U-statistic.
4) Approximate F-statistic (this is a transformation of Wilk’s lambda).
5) Mahalanobi’s D-distance.
6) F-matrix that contains F-values computed from the Mahalanobi’s D-distance.
7) The classification functions.
The classification functions can be used a posteriori to classify cases within groups; the case is assigned to the group whose classification function has the largest value.
This can be done in two ways:
1) With a prediction program of the phenomenon that uses the classification functions for new cases.
2) With an assessing program that classifies the same cases of the sample from which the functions were obtained (thus, the starting sample is re-classified).
The classification score for each group is computed from the discriminant function coefficients (data are multiplied by the coefficients and the constant term is added). The case is classified within the group with the highest classification score. The score can also be expressed as probabilities: q is the number of groups and Sij is the classification score for the “ith” case of the “jth” group, so that the posterior probability that case i belongs to j group is:
![]() .
.
The prediction programs mentioned in 3.1 were thus made.
The last step, besides giving the results obtained in each step, also produces:
1) The classification matrix.
2) The jackknifed classification matrix.
3) A summary table: this contains a one-line summary for each step, including the F-to-enter (or F-to-remove) for the variable entered (or removed), Wilk’s lambda or U-statistic, the approximate F-statistic and the degrees of freedom.
The SDA program also solves others issues that do not fall within the scope of this paper.
Appendix B: Forecast Evaluation Methods
For calculating the percentages of success “A” and the success degree or skill-score “S”, the following notation was established:
N = number of forecasts
(A) = Number of times that YES was forecasted
(B) = Number of times that NO was forecasted
(a) = Number of times that YES was observed
(b) = Number of times that NO was observed
Also,
(AB) = Number of times that YES was forecasted and YES occurred (hit)
(Ab) = Number of times that YES was forecasted and NO occurred (false alarm)
(aB) = Number of times that NO was forecasted and YES occurred (surprise)
(ab) = Number of times that NO was forecasted and NO occurred (hit)
Then, success percentage is calculated:
![]() .
.
The success degree or skill-score is defined:
![]() ,
,
with
![]() ,
,
“L” being the amount of success by climatological chance, which indicates how many forecasts would a neophyte guess by chance. The success degree “S” (skill-score) filters those guesses at random.
If the amount of success of the implemented prediction methods were equal to the amount of success by climatological chance, then S would be equal to zero. Conversely, S equal to one would mean total success.
For evaluating the forecasting methods, the correlation coefficient rp between the probabilities xi and the observed relative frequencies yi was calculated. It is defined:
![]() .
.
where γ is the number of the different probabilities in use, σxi is the variance of the probabilities, and σyi is the variance of the relative frequencies.
For the forecast to be useful, rp must be positive. In addition, if the N number of forecast increases, the frequency of zonda wind occurrence will approach the climatological frequency; this permits obtaining a greater score of the rp value but the forecast is less useful.
That is why the mean absolute value is calculated for the difference between the square of the forecasted probability and 1 if zonda occurs, or 0 if zonda does not occur. This index, proposed by Brier, forces the forecast to approach the extreme probabilities (probability 0 corresponds to the deterministic forecast NO, and 1 to YES).
![]()
The lower the mean D value is, the better the forecast will be. Absolute deterministic success is reached if mean D is equal to 0.