A Singular Values Based Newton Method for Linear Complementarity Problems ()
Received 3 November 2015; accepted 28 December 2015; published 31 December 2015

1. Introduction
Given a matrix 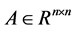 and a vector
and a vector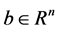 , the problem of finding vectors
, the problem of finding vectors 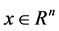 such that
such that
 (1.1)
(1.1)
is called the linear complementarity problem (LCP). We call the problem the LCP (A, b). It is well known that several problems in optimization and engineering can be expressed as LCPs. Cottle, Pang, and Stone [1] [2] provide a thorough discussion of the problem and its applications, as well as providing solution techniques.
There are a large number of general purpose methods for solving linear complementarity problems. We can divide these methods into essentially two categories: direct methods, such as pivoting techniques [1] [2] , and iterative methods, such as Newton iteration [2] [3] and interior point algorithms [4] .
The penalty method has been used an LCP (or, equivalently, a variational inequality) [5] [6] . The paper [7] [8] constructed a nonlinear penalized Equation (1.2) corresponding to variational inequality.
Find 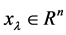 such that
such that
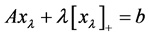 (1.2)
(1.2)
where 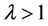 is the penalized parameter,
is the penalized parameter,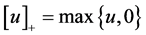 .
.
The nonlinear penalized problems (1.2) corresponding to the linear complementarity problem (1.1), which its research has achieved good results. Wang [9] [10] , Yang [11] and Li [12] [13] was extended to a general form of (1.2) to present a power penalty function
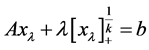 (1.3)
(1.3)
approach to the linear complementarity problem. For the penalty Equation (1.2) Li [14] proved the solution to this equation converges to that of the linear complementarity problem when the singular values of A exceed 1 and Han [15] the interval matrix 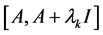 is regular. It is worth mentioning that the penalty technique has been widely used solving nonlinear programming, but it seems that there is a limited study for LCP.
is regular. It is worth mentioning that the penalty technique has been widely used solving nonlinear programming, but it seems that there is a limited study for LCP.
Some words about our notation: I refers to the identity matrix, and 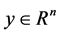 are column vectors, yT refers to the transpose of the y, we denote by
are column vectors, yT refers to the transpose of the y, we denote by 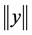 the Euclidian norm.
the Euclidian norm.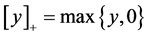 , that generalized Jacobian
, that generalized Jacobian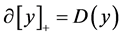 , where
, where 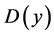 denotes diagonal matrix, On the diagonal elements with component 1, 0 or
denotes diagonal matrix, On the diagonal elements with component 1, 0 or ![]() corresponding to the component of y which is positive , negative or zero, respectively.
corresponding to the component of y which is positive , negative or zero, respectively.
2. Generalized Newton Method
In this section, we will propose that a new generalized Newton method based on the nonlinear penalized Equation (1.2) for solving the linear complementarity problem.
Proposition 1 [15] . ![]() equivalent to
equivalent to![]() , where
, where
![]()
Proposition 2. ![]() has a unique solution if the singular values of A exceed 0.
has a unique solution if the singular values of A exceed 0.
Proof: Since the singular values of A exceed 0, then A is a positive definite matrix,and ![]() is positive definite, then
is positive definite, then ![]() is positive definite, then
is positive definite, then ![]() has a unique solution. □
has a unique solution. □
Let us note
![]() (2.1)
(2.1)
Thus, nonlinear penalized Equation (1.2) is equivalent to the equation![]() .
.
A generalized Jacobian ![]() of
of ![]() is given by
is given by
![]() .
.
where ![]() is a diagonal matrix whose diagonal entries are equal 1, 0 or a real number
is a diagonal matrix whose diagonal entries are equal 1, 0 or a real number ![]() depending on whether the corresponding component of
depending on whether the corresponding component of ![]() is positive, negative, or zero. The generalized Newton method for finding a solution of the equation
is positive, negative, or zero. The generalized Newton method for finding a solution of the equation ![]() consists of the following iteration:
consists of the following iteration:
![]()
equavelently
![]() (2.2)
(2.2)
Algorithm 1
Step 1: Choose an arbitrary initial point![]() ,
, ![]() and given
and given![]() ,
, ![]() ,
, ![]() , let
, let![]() ;
;
Step 2: for the![]() , computer
, computer ![]() by solving (2.2).
by solving (2.2).
Step 3: If![]() , terminate. Otherwise,
, terminate. Otherwise, ![]() go to step 2.
go to step 2.
Step4: If![]() , terminate,
, terminate, ![]() is solution of LCP. Otherwise let
is solution of LCP. Otherwise let![]() ,
, ![]() let
let![]() , go to 2.
, go to 2.
3. The Convergence of the Algorithm
We will show that the sequence ![]() generated by generalized Newton iteration (2.2) converges to an ac-
generated by generalized Newton iteration (2.2) converges to an ac-
cumulation point ![]() associated with
associated with![]() . First, we establish boundness of the sequence
. First, we establish boundness of the sequence ![]() for any
for any ![]() generated by the Newton iterates (2.2) and hence the existence of accumulation point at each generalized Newton iteration.
generated by the Newton iterates (2.2) and hence the existence of accumulation point at each generalized Newton iteration.
Theorem 1: Suppose the singular values of M exceed 0. Then, the sequence ![]() generated by Algorithm 1 is bounded. Consequently, there exits an accumulation points
generated by Algorithm 1 is bounded. Consequently, there exits an accumulation points ![]() such that
such that![]() .
.
Proof. Suppose that sequence ![]() is unbounded, Thus, there exists an infinite nonzero subsequence
is unbounded, Thus, there exists an infinite nonzero subsequence ![]() such that
such that
![]() ,
, ![]() and
and ![]()
where ![]() is main diagonal element of diagonal matrix which is
is main diagonal element of diagonal matrix which is![]() .
.
We know subsequence ![]() is bounded. Hence, exists convergence subsequence and assume that convergence point is
is bounded. Hence, exists convergence subsequence and assume that convergence point is![]() , and satisfy
, and satisfy
![]() .
.
Letting ![]() yields
yields
![]()
Since the singular values of A exceed 0, then A is regular, and ![]() is regular, we know that
is regular, we know that ![]() is exists and hence
is exists and hence![]() , contradicting to the fact that
, contradicting to the fact that![]() . Consequently, the sequence
. Consequently, the sequence ![]() is bounded and there exists an accumulation point
is bounded and there exists an accumulation point ![]() of
of ![]() such that
such that
![]() . □
. □
Under a somewhat restrictive assumption we can establish finite termination of the generalized Newton iteration at a penalized equation solution as follows.
Theorem 2: Suppose the singular values of A exceed 0 and ![]() holds for all suffi-
holds for all suffi-
ciently large![]() , then the generalized Newton iteration (2.2) linearly converges from any starting point
, then the generalized Newton iteration (2.2) linearly converges from any starting point ![]() to a solution
to a solution ![]() of the nonlinear penalized Equation (1.2).
of the nonlinear penalized Equation (1.2).
Proof. Similar to the proof of Theorem
4 in
[15] . □
Theorem 3: Suppose the singular values of A exceed 0 and ![]() holds, then Algorithm
holds, then Algorithm
1 linearly converges from any starting point ![]() to a solution
to a solution ![]() of the
of the ![]() (1.1).
(1.1).
Proof. Similar to the proof of Theorem
5 in
[15] . □
4. Numerical Experiments
In this section, we give some numerical results in order to show the practical performance of Algorithm 2.1 Numerical results were obtained by using Matlab R2007(b) on a
1G
RAM, 1.86 Ghz Intel Core 2 processor. Throughout the computational experiments, the parameters were set as![]() ,
, ![]() ,
,![]() .
.
Example 1: The matrix A of linear complementarity problem ![]() of as follows (This example appears in the Geiger and Kanzow [16] , Jiang and Qi [17] , YONG Long-quan, DENG Fang-an, CHEN Tao [18] and Han [15] ):
of as follows (This example appears in the Geiger and Kanzow [16] , Jiang and Qi [17] , YONG Long-quan, DENG Fang-an, CHEN Tao [18] and Han [15] ):
![]() ,
, ![]()
The computational results are shown in Table 1. This ![]() is initial point, k is number of inner iterations, the outer iteration number is m,
is initial point, k is number of inner iterations, the outer iteration number is m, ![]() is iteration results.
is iteration results.
Example 2: The matrix A of linear complementarity problem ![]() of as follows:
of as follows:
![]() ,
, ![]()
Optimal solution of this problem is![]() . The computational results are shown in Table 2. This
. The computational results are shown in Table 2. This ![]() is initial point, k is number of inner iterations, the outer iteration number is m,
is initial point, k is number of inner iterations, the outer iteration number is m, ![]() is iteration results.
is iteration results.
Example 3: The matrix A of linear complementarity problem ![]() of as follows (This example appears in the Geiger and Kanzow [16] , Jiang and Qi [17] , YONG Long-quan, DENG Fang-an, CHEN Tao [18] and Han [15] ):
of as follows (This example appears in the Geiger and Kanzow [16] , Jiang and Qi [17] , YONG Long-quan, DENG Fang-an, CHEN Tao [18] and Han [15] ):
![]() ,
, ![]()
The computational results are shown in Table 3. This ![]() is initial point, k is number of inner iterations, the outer iteration number is m,
is initial point, k is number of inner iterations, the outer iteration number is m, ![]() is iteration results.
is iteration results.
NOTES
![]()
*This work supported by the Science Foundation of Inner Mongolia in China (2011MS0114).