Received 27 August 2015; accepted 21 December 2015; published 25 December 2015

1. Introduction to Inequality Merging
An integer program (IP) is a common type of optimization problem, defined as maximize 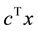 subject to
subject to 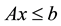 and
and 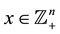 where
where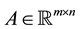 ,
, 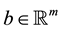 , and
, and 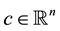 where m and n are integers both greater than or equal to 1. Define
where m and n are integers both greater than or equal to 1. Define 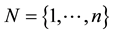 as the set of indices of an IP.
as the set of indices of an IP.
One frequently studied IP is the 0 - 1 knapsack problem (KP), defined as maximize 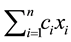 subject to
subject to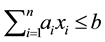 , and
, and 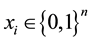 where c and
where c and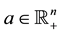 ,
,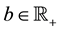 . The multiple knapsack (MK) problem has
. The multiple knapsack (MK) problem has
multiple knapsack constraints and is defined as maximize 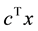 subject to
subject to 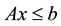 and
and 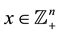 where
where![]() ,
, ![]() , and
, and![]() .
.
Solutions to KP and MK problems support a wide variety of real-world applications, including examples in Ahuja and Cunha [1] , Chang and Lee [2] , Dawande et al. [3] , Dizdar et al. [4] , Kellerer and Strusevich [5] , Martello and Toth [6] , Shachnai and Tamir [7] , and Szeto and Lo [8] . This paper focuses on MK problems.
A half space is![]() , and a polyhedron is defined as the intersection of finitely many half
, and a polyhedron is defined as the intersection of finitely many half
spaces. A set ![]() is convex if and only if
is convex if and only if ![]() and
and ![]() implies
implies ![]() for every
for every![]() . A polyhedron is convex, and the convex hull of S,
. A polyhedron is convex, and the convex hull of S, ![]() , is the intersection of all convex sets that contain S.
, is the intersection of all convex sets that contain S.
Let P be the set of feasible points of an integer program, where![]() . Define
. Define
![]() and
and ![]() as the feasible regions of the knapsack and
as the feasible regions of the knapsack and
multiple knapsack problems, respectively where ![]() and
and![]() .
.
A well-known technique to improve solution times for IP problems is the generation of valid inequalities. An
inequality ![]() is a valid inequality for
is a valid inequality for ![]() if every
if every ![]() satisfies the inequality. If the
satisfies the inequality. If the
valid inequality separates the linear relaxation solution from the convex hull of the IP, then it is called a cutting plane. The linear relaxation is the IP with the integrality restriction eliminated. The theoretically best cutting planes define facets of![]() , but any cutting plane that separates the linear relaxation from
, but any cutting plane that separates the linear relaxation from ![]() may be computationally useful. A thorough explanation of such results is in Nemhauser and Wolsey [9] .
may be computationally useful. A thorough explanation of such results is in Nemhauser and Wolsey [9] .
For a MK problem, a cover cut may be generated in one or more of the m constraints. A set ![]() is a
is a
cover for row ![]() if
if![]() . The corresponding cover inequality is valid for
. The corresponding cover inequality is valid for ![]() and takes the form
and takes the form![]() . Cover cuts have been studied extensively by Balas and Zemel [10] , De Farias
. Cover cuts have been studied extensively by Balas and Zemel [10] , De Farias
et al. [11] , Louveaux and Weismantel [12] , Nemhauser and Vance [13] , and Park [14] . Knowledge of cover cuts is critical to this research.
Many such covers may exist and pseudo-costing strategies provide a prioritized variable ordering. Pseudo- costing strategies for integer programming problems were studied by Benichou, et al. in [15] and Gauthier and Ribiere in [16] . Refalo used pseudo-cost strategies to improve constraint programming in [17] , and Achterberg, et al. developed reliability branching rules for IPs as an extension of pseudo-costing in [18] .
In some instances, cover inequalities may be strengthened through lifting. Gomory introduced the technique in [19] , taking a valid inequality of a restricted space and tilting it to become a valid inequality of a higher dimensional space. Substantial bodies of research have extended lifting to several categories such as exact up-lifting (Cho et al. [20] , Gutierrez [21] , Hammer et al. [22] , and Wolsey [23] ), exact simultaneous up-lifting (Easton and Hooker [24] , Kubik [25] , and Zemel [26] ), exact sequential down and middle lifting by Wolsey [23] , sequence dependent lifting (Atamtürk [27] , Gu et al. [28] -[30] , and Shebalov and Klabjan [31] ), and other approximate lifting methods (Balas [32] and Weismantel [33] ).
Theoretical foundations for inequality merging were first introduced by Hickman and Easton in [34] . Although merging appears similar to lifting, it yields new cutting planes that are not attainable through straight- forward applications of known lifting techniques. Their paper creates a single cutting plane by merging two inequalities. This merged inequality can be theoretically stronger than the original inequalities, and it may induce a facet under certain conditions.
This paper extends the idea of inequality merging by focusing on cover inequalities in MK problems. Information from two or more cover inequalities in an MK instance may be merged into a single cutting plane. In some instances, simultaneous merging of cover inequalities may occur across multiple rows at the same time.
The next section describes the process of cover inequality merging for MK instances and provides theoretical results and examples. The third section offers the results of a computational study that highlights the computa- tional benefits of employing merged cover inequalities in test MK problems. The final section offers some directions for future research.
2. Theory and Examples of Merging Cover Inequalities
It is straightforward to find cover inequalities in MK instances and merging requires two covers, called host and donor. Let ![]() be a cover in row r and
be a cover in row r and ![]() be a cover in row s for some
be a cover in row s for some![]() . Thus,
. Thus,
the cover inequalities ![]() and
and ![]() are valid inequalities of
are valid inequalities of![]() .
.
Merging the host and donor cover inequalities occurs on binary variable ![]() where
where ![]() or if
or if
![]() , then
, then![]() . Since
. Since ![]() is bounded by 1 and
is bounded by 1 and![]() , it follows that
, it follows that ![]() could be replaced in host cover inequality with the
could be replaced in host cover inequality with the ![]() indices with coefficients
indices with coefficients![]() . Thus, a merged cover inequality has the form
. Thus, a merged cover inequality has the form![]() .
.
If the merged inequality is valid, then this inequality includes more nonzero coefficients than either ![]() or
or![]() . The question remains as to whether or not the merged inequality is valid. The following theorem provides conditions for its validity.
. The question remains as to whether or not the merged inequality is valid. The following theorem provides conditions for its validity.
Theorem 1. Let ![]() be a cover from row r and
be a cover from row r and ![]() be a cover from some row s in a MK instance such that
be a cover from some row s in a MK instance such that![]() . Define index
. Define index ![]() as the merging index with the restriction that if
as the merging index with the restriction that if![]() , then
, then![]() . If
. If ![]() is a cover in at least one row of the MK
is a cover in at least one row of the MK
instance for each![]() , then the merged cover inequality,
, then the merged cover inequality, ![]() ,
,
is valid for![]() .
.
Proof. Let ![]() be any point in
be any point in![]() . Define
. Define![]() . If
. If![]() , then
, then ![]() because
because
![]() is a cover in some constraint for each
is a cover in some constraint for each![]() . Thus,
. Thus,
![]() . If
. If![]() , then
, then ![]() since
since ![]() is a cover. Thus,
is a cover. Thus, ![]() and the result follows.
and the result follows. ![]()
Theorem 1 describes which indices can be used to create a donor cover. These candidate indices can be easily found based upon a ![]() threshold, which is associated with the host cover inequality and the merging variable. Given a host cover
threshold, which is associated with the host cover inequality and the merging variable. Given a host cover ![]() in row r and a designated merging variable
in row r and a designated merging variable![]() , then
, then
![]() . The purpose of
. The purpose of ![]() is to rapidly identify indices that can be used to create a donor cover from any row s. Define these potential donor indices as
is to rapidly identify indices that can be used to create a donor cover from any row s. Define these potential donor indices as![]() . If
. If
![]() is a cover and
is a cover and![]() , then merging the host and donor cover on
, then merging the host and donor cover on ![]() results in a valid merged
results in a valid merged
inequality as shown in the following theorem.
Theorem 2. Given a multiple knapsack instance, a host cover ![]() from row r and a merging variable
from row r and a merging variable ![]() with
with![]() . Let
. Let ![]() be a cover in some row s such that
be a cover in some row s such that ![]() for all
for all![]() , then
, then
![]() is a valid inequality of
is a valid inequality of![]() .
.
Proof. Assume![]() ,
, ![]() is a cover in row r,
is a cover in row r, ![]() is a cover in some row s and
is a cover in some row s and![]() . Define
. Define
![]() . Since
. Since ![]() is a cover,
is a cover,![]() . The proof divides into two cases,
. The proof divides into two cases, ![]() and
and
![]() .
.
First, assume![]() . Thus,
. Thus, ![]() for all
for all![]() . Since
. Since![]() ,
,
![]() . Thus,
. Thus,![]() . Every
. Every ![]() has the
has the
property that ![]() and so
and so ![]() for all
for all![]() . Consequently,
. Consequently,
![]() .
.
Second, assume![]() . Since Cdonor is a cover in row s,
. Since Cdonor is a cover in row s,![]() . Thus,
. Thus,![]() .
.
Consequently,![]() .
.
These two cases are exhaustive. Therefore every ![]() satisfies
satisfies
![]() and this merged inequality is valid for
and this merged inequality is valid for![]() .
. ![]()
To identify valid merged cover inequalities, the user must identify a host cover, ![]() and a merged index
and a merged index![]() . Some selections for
. Some selections for ![]() and a merged variable
and a merged variable ![]() may not allow a candidate donor inequality to exist. The Reducing
may not allow a candidate donor inequality to exist. The Reducing ![]() Algorithm changes
Algorithm changes ![]() to increase the likelihood of the existence of an appropriate donor cover.
to increase the likelihood of the existence of an appropriate donor cover.
The input to the Reducing ![]() Algorithm is a multiple knapsack instance, a valid host cover from row r and a merging variable
Algorithm is a multiple knapsack instance, a valid host cover from row r and a merging variable ![]() with
with![]() . In addition, a threshold
. In addition, a threshold ![]() is provided. The output of this algorithm is a new host cover inequality and a new merging variable. These are denoted by
is provided. The output of this algorithm is a new host cover inequality and a new merging variable. These are denoted by ![]() and
and![]() , respectively.
, respectively.
Reducing ![]() Algorithm
Algorithm
![]()
If the Reducing ![]() Algorithm terminates successfully, then
Algorithm terminates successfully, then ![]() is a cover because it satisfies the
is a cover because it satisfies the
condition that![]() . When this happens, the last index q added to
. When this happens, the last index q added to ![]() becomes the newly deter-
becomes the newly deter-
mined overlapped variable![]() , and
, and![]() . Since
. Since![]() , smaller
, smaller ![]() coef-
coef-
ficients may identify acceptable additional variables for use in![]() . This increases the likelihood of achieving a valid
. This increases the likelihood of achieving a valid![]() , thus increasing the opportunity for construction of a merged cutting plane inequality.
, thus increasing the opportunity for construction of a merged cutting plane inequality.
In some instances, the Reducing ![]() Algorithm terminates successfully with a new cover
Algorithm terminates successfully with a new cover ![]() and a new value
and a new value![]() , but it may not have a sufficient number indices in
, but it may not have a sufficient number indices in ![]() to construct
to construct![]() . If this happens, the
. If this happens, the
Reducing ![]() Algorithm may be used iteratively until a suitable
Algorithm may be used iteratively until a suitable ![]() is attained.
is attained.
Observe that the Reducing ![]() Algorithm also requires a careful selection of
Algorithm also requires a careful selection of ![]() to achieve stronger results in many instances. A small value of
to achieve stronger results in many instances. A small value of ![]() tends to allow indices with small a coefficients to enter
tends to allow indices with small a coefficients to enter![]() . When this happens, the size of
. When this happens, the size of ![]() may become undesirably large or fail to generate a cover. Including too many variables in the host cover results in fewer candidate indices in
may become undesirably large or fail to generate a cover. Including too many variables in the host cover results in fewer candidate indices in![]() .
.
High values of ![]() may allow few (or zero) new candidate indices for inclusion in
may allow few (or zero) new candidate indices for inclusion in![]() . In such instances, it is more likely that the reducing
. In such instances, it is more likely that the reducing ![]() algorithm fails to return a new
algorithm fails to return a new ![]() and/or fails to reduce the value of
and/or fails to reduce the value of![]() . Even if the algorithm succeeds, higher values of
. Even if the algorithm succeeds, higher values of ![]() tend to result in relatively smaller reductions in
tend to result in relatively smaller reductions in![]() , possibly requiring multiple calls to this procedure when a valid merged inequality is not yet attainable. Given this sensitivity to
, possibly requiring multiple calls to this procedure when a valid merged inequality is not yet attainable. Given this sensitivity to![]() , a careful selection of
, a careful selection of ![]() is required. For practical purposes, it is recommended to consider values of
is required. For practical purposes, it is recommended to consider values of ![]() between 0.3 and 0.7.
between 0.3 and 0.7.
The Reducing ![]() Algorithm is a linear algorithm for each specified
Algorithm is a linear algorithm for each specified ![]() value. The initialization requires
value. The initialization requires
![]() . The main step could search through all other indices, so it performs in
. The main step could search through all other indices, so it performs in ![]() effort. Thus,
effort. Thus,
the algorithm runs in![]() , which is linear for a fixed
, which is linear for a fixed![]() .
.
2.1. Merging over Multiple Donor Covers Simultaneously
This section presents a method to strengthen the previous results by merging on multiple donor covers at the same time. Conditions are provided to create valid inequalities from merging over three or more cover inequa- lities simultaneously. Another algorithm is presented to search for the strongest merging coefficients among multiple potential donor rows in the MK instance.
Simultaneous merging over multiple donor covers begins with a ![]() cover from a MK constraint with
cover from a MK constraint with
![]() and its associated
and its associated ![]() and set
and set![]() . The inequality
. The inequality ![]() is likely to be valid for any
is likely to be valid for any ![]() where
where ![]() is any cover from any constraint of the MK instance with
is any cover from any constraint of the MK instance with![]() . Thus, the strongest such inequality would select
. Thus, the strongest such inequality would select ![]() where
where ![]() and
and ![]() is the
is the
maximum cardinality cover from any row.
The check of validity must assure that there does not exist a feasible point which violates this new inequality.
Prior to this result, define![]() ,
, ![]() and
and![]() .
.
Theorem 3. Let ![]() be a cover from a MK constraint with
be a cover from a MK constraint with![]() , corresponding value
, corresponding value ![]() and
and
associated set![]() . Then the inequality
. Then the inequality ![]() is valid for
is valid for ![]() for any
for any ![]() where
where ![]() is any cover from any constraint of the MK instance as long as one of
is any cover from any constraint of the MK instance as long as one of
the following conditions holds
1) ![]()
2) ![]() for all integer
for all integer![]() .
.
Proof. Let![]() . Since
. Since![]() , then
, then ![]() is a cover in row r. If
is a cover in row r. If![]() , then
, then![]() . Thus,
. Thus, ![]() for every value of
for every value of![]() .
.
Assume 1) is true. If![]() , then
, then ![]() because 1) is true and
because 1) is true and ![]() is bounded by 1. Consequently,
is bounded by 1. Consequently,![]() .
.
Assume 2) is true. Let![]() . Thus
. Thus![]() . By 2)
. By 2) ![]() and thus
and thus ![]() . Thus,
. Thus,![]() .
. ![]()
An immediate result of Theorem 3 is an algorithm to merge over multiple donor covers simultaneously. This algorithm explores all rows to determine the smallest eligible covers of each merging variable in![]() . This translates into the stronger coefficients for each merging variable. The input to the Donor Coefficient Streng- thening Algorithm (DCSA) is a MK instance, a host cover
. This translates into the stronger coefficients for each merging variable. The input to the Donor Coefficient Streng- thening Algorithm (DCSA) is a MK instance, a host cover ![]() from row r and an index
from row r and an index![]() .
.
Donor Coeffcient Strengthening Algorithm
![]()
DCSA identifies the smallest donor covers possible for each index in ![]() from each row in the MK
from each row in the MK
instance using the indices sorted in each row by the a values. Observe that DCSA does not guarantee a valid inequality, but it does identify the strongest possible merged inequality. If the reported merged inequality satisfies a condition of Theorem 3, then it is a valid inequality.
DCSA’s computational effort required for the initialization is![]() . The main step requires
. The main step requires![]() . Thus DCSA’s effort is
. Thus DCSA’s effort is![]() . Although this is a cubic run time, DCSA performs quickly in practice.
. Although this is a cubic run time, DCSA performs quickly in practice.
2.2. Inequality Merging Example
The following example demonstrates the theoretical concepts discussed earlier. Consider multiple knapsack constraints of the form ![]() with
with ![]() and
and ![]() where
where
![]()
and
![]()
Designate the first constraint as the host constraint, ![]() and let the host cover be
and let the host cover be![]() . If the merging index is
. If the merging index is![]() , then
, then![]() . Because
. Because ![]() and
and ![]() are all greater than or equal to 10, the candidate indices for the donor cover are restricted to
are all greater than or equal to 10, the candidate indices for the donor cover are restricted to![]() .
.
No subset of ![]() is a cover. The Reducing
is a cover. The Reducing ![]() Algorithm is used to change the host cover to create a
Algorithm is used to change the host cover to create a
smaller![]() . Let
. Let![]() , then the Reducing
, then the Reducing ![]() Algorithm seeks a host cover with a
Algorithm seeks a host cover with a ![]() value that is less than
value that is less than
or equal to 5. In this case {5} is eliminated from the host cover, and the host cover adds an index with a coefficient between 5 and 9. Indices 10, 11, 12, and 13 are all suitable and index 11 is added to![]() . However,
. However, ![]() is not a cover. Including either index 12 or 13 would create a host cover and
is not a cover. Including either index 12 or 13 would create a host cover and![]() . The new value for
. The new value for ![]() is reduced exactly by the coefficient of the first added index,
is reduced exactly by the coefficient of the first added index,![]() . Thus
. Thus![]() , and the candidate indices for the donor cover are
, and the candidate indices for the donor cover are![]() . There exist several covers in constraint two from this candidate set. One such cover is
. There exist several covers in constraint two from this candidate set. One such cover is![]() . Since a donor cover now exists,
. Since a donor cover now exists, ![]() becomes
becomes![]() .
.
The algorithm has now determined a host and donor cover that can be merged. Merging the host with the donor on ![]() yields (1), a valid inequality according to Theorem 2.
yields (1), a valid inequality according to Theorem 2.
![]() (1)
(1)
The following arguments demonstrate Theorems 1 and 2 in practice. Verifying the validity of (1) requires that ![]() is a cover for some constraint for every
is a cover for some constraint for every![]() . The sum of the
. The sum of the ![]() coeffi- cients is 76. Clearly
coeffi- cients is 76. Clearly ![]() is a cover in the first knapsack as long as
is a cover in the first knapsack as long as ![]() and
and![]() . Since all candidate donor indices have
. Since all candidate donor indices have![]() , (1) is verified as a valid inequality of
, (1) is verified as a valid inequality of![]() .
.
Observe that numerous other minimal donor covers exist when![]() . Two other examples are
. Two other examples are ![]() and
and![]() . Accordingly, we could merge each of these cover inequalities with the host cover inequality yielding the following valid merged inequalities
. Accordingly, we could merge each of these cover inequalities with the host cover inequality yielding the following valid merged inequalities
![]() (2)
(2)
![]() (3)
(3)
Each of these merged inequalities remove linear relaxation points and are thus cutting planes. For instance,
the point (1,1,1,1,0,0,0,0,0,![]() ,1,0,0,0) is eliminated by each of these merged inequalities. Additionally, it is
,1,0,0,0) is eliminated by each of these merged inequalities. Additionally, it is
simple to find points that are satisfied by two of the three merged inequalities, but eliminated by the other inequality. Thus, each merged inequality is eliminating distinct regions of the linear relaxation space.
Returning to the original host cover, it is also possible to generate new families of merged inequalities if merging on ![]() instead of
instead of![]() . By changing the index selected for merging,
. By changing the index selected for merging, ![]() with corresponding candidate donor indices
with corresponding candidate donor indices![]() . Similar to the examples shown previously, many possible new donor covers now exist. For instance,
. Similar to the examples shown previously, many possible new donor covers now exist. For instance, ![]() yields
yields
![]() (4)
(4)
The idea of ![]() guarantees validity, but it is not necessary to merge covers. Consider
guarantees validity, but it is not necessary to merge covers. Consider ![]() with
with![]() . In the first constraint,
. In the first constraint, ![]() is a cover and so {5} is a candidate index. The second con- straint has several relevant covers:
is a cover and so {5} is a candidate index. The second con- straint has several relevant covers:![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . Thus, the candidate indices are now
. Thus, the candidate indices are now![]() . One such cover in the second constraint is
. One such cover in the second constraint is![]() , which results in the following merged constraint
, which results in the following merged constraint
![]() (5)
(5)
The authors believe that such constraints may be more useful computationally since they are incorporating
covers from multiple constraints to obtain validity. For instance, the linear relaxation point (1,1,1,![]() ,0,1,0,0,
,0,1,0,0,![]() , 0,0,0,0,
, 0,0,0,0,![]() ) is eliminated by this inequality.
) is eliminated by this inequality.
To demonstrate Theorem 3, an additional row is added to this example. Now consider the following multiple knapsack instance
![]()
and
![]()
Again, consider ![]() with
with ![]() and
and![]() . For each index in
. For each index in![]() , DCSA forces this index as the first element in a cover and then adds other indices according to the sorted order for each row. Observe that
, DCSA forces this index as the first element in a cover and then adds other indices according to the sorted order for each row. Observe that ![]() is not a cover in row 1, so only rows 2 and 3 are considered.
is not a cover in row 1, so only rows 2 and 3 are considered.
For index 5, the smallest covers are ![]() and
and ![]() in rows 2 and 3, respectively. Continuing this logic for each of the other indices results in Table 1. The smallest covers are listed in the order in which DCSA adds indices to the cover.
in rows 2 and 3, respectively. Continuing this logic for each of the other indices results in Table 1. The smallest covers are listed in the order in which DCSA adds indices to the cover.
Thus the simultaneous merged inequality is
![]() (6)
(6)
Observe that this new inequality dominates all of the previous inequalities. Furthermore, to achieve this inequality all rows are necessary. For instance, the smallest cover in row 3 containing index 6 has 6 indices and thus row two is necessary. Similarly, the smallest cover in row 2 containing index 7 has 6 indices and thus row 3 is necessary.
![]()
Table 1. Applying DCSA to find strongest coefficients.
To argue validity of (6), consider Theorem 3. Since![]() , 1) is not satisfied. For 2), observe that
, 1) is not satisfied. For 2), observe that
![]() and
and![]() . Continuing this process yields
. Continuing this process yields![]() ,
, ![]() , and
, and![]() .
.
Determining the values for ![]() yield that
yield that![]() ,
, ![]() , and
, and ![]() do not exist as
do not exist as![]() . However,
. However,
![]() because it requires five variables with coefficients in
because it requires five variables with coefficients in ![]() to be set to one to arrive at a value strictly larger than
to be set to one to arrive at a value strictly larger than![]() . Since
. Since![]() ,
,![]() .
.
Since![]() ,
, ![]() , and
, and ![]() do not exist, only
do not exist, only ![]() and
and ![]() are determined. The value of
are determined. The value of ![]() . Similarly,
. Similarly,![]() . Condition 2) of Theorem 3 checks
. Condition 2) of Theorem 3 checks ![]() and
and![]() . Thus, (6) meets condition 2) of Theorem 3 and it is valid. As a note, observe that checking
. Thus, (6) meets condition 2) of Theorem 3 and it is valid. As a note, observe that checking ![]() is always true by the definition of
is always true by the definition of![]() .
.
The final benefit of this example demonstrates that merging cover inequalities are not an immediate extension of known methods. There are similarities between inequality merging and some categories of lifting. Any type of sequential lifting has integer coefficients [35] , and sequence independent lifting would require all non-cover coeffi- cients in this example to be 0 [30] . Thus neither of these methods generate (6). While simultaneous lifting could theoretically generate (6) [21] , it would require starting with the trivial cutting plane ![]() and furthermore have a perfect guess of proper weights. Consequently, inequality merging yields inequalities similar to (6), which are extremely unlikely to be produced by lifting techniques.
and furthermore have a perfect guess of proper weights. Consequently, inequality merging yields inequalities similar to (6), which are extremely unlikely to be produced by lifting techniques.
The general inequality merging presented by Hickman and Easton in [34] did not merge multiple donor covers simultaneously, and it could not obtain (6). Inequality merging is also fundamentally different from other popular cutting plane generation techniques such as C-G cuts (Chvátal [36] and Gomory [37] ), disjunctive cuts (Balas and Perregaard [38] ), Gomory cuts (Gomory [37] ), or superadditive cuts (Gomory and Johnson [39] and Wolsey [40] ). Theoretically, these methods could generate (6), but they would require numerous iterative applications to find this cutting plane. Such a result is unlikely to occur without the consultation of an oracle to select initial inequalities, weights or other necessary input.
A single call to DCSA creates (6) and requires ![]() effort. Thus, merging over cover inequalities is a new method to obtain previously unknown inequalities. Given the large size of most multiple knapsack problems, the flexibility of the construction algorithms are usually capable of finding strong candidate
effort. Thus, merging over cover inequalities is a new method to obtain previously unknown inequalities. Given the large size of most multiple knapsack problems, the flexibility of the construction algorithms are usually capable of finding strong candidate ![]() and
and ![]() inequalities. The next section provides the results of a computational study, demonstrating the practical effectiveness of inequality merging on benchmark multiple knapsack problems.
inequalities. The next section provides the results of a computational study, demonstrating the practical effectiveness of inequality merging on benchmark multiple knapsack problems.
3. Computational Study
This computational study compares solution times for multiple knapsack problems both with and without the use of merged inequalities. The instances chosen for this study are the MK instances from the OR-Library [41] , developed by Chu and Beasley in 1998 [42] . The majority of these instances are either trivially solved or too computationally intensive for an optimal solution. Thus, this study focuses on medium sized instances contained in files mknapcb2 (![]() and
and![]() ) and mknapcb5 (
) and mknapcb5 (![]() and
and![]() ).
).
Each file contains 30 instances divided into groups of 10 based upon a tightness ratio, which is equal to
![]() . The tightness ratio is approximately equal for all constraints and is 0.25 for the first 10 instan-
. The tightness ratio is approximately equal for all constraints and is 0.25 for the first 10 instan-
ces, 0.5 for the second ten instances, and 0.75 for the final ten instances. For this computational study, the first ten instances are only considered. When the tightness ratio is 0.5 or higher, ![]() tends to include too many variables. Since the variables in
tends to include too many variables. Since the variables in ![]() are prohibited from being in
are prohibited from being in![]() , higher tightness ratios reduce the size of
, higher tightness ratios reduce the size of![]() , which decreases the likelihood of finding a suitable donor cover in any row.
, which decreases the likelihood of finding a suitable donor cover in any row.
The study considers a variety of implementation strategies including the number of merged inequalities added, the possibility of overlapping rows when multiple cuts are added, the option to use the Donor Coefficient Strengthening Algorithm when constructing merged inequalities, and different pseudocosting techniques. The psuedocosting techniques provide an order for selecting indices for cover inequalities. Three options are con- sidered: sorting on the reduced costs, sorting on the a coefficient values, and sorting on equal weights for both reduced costs and a coefficient values. More details of these methods and computational results are described in [43] .
The experimentation compares computational effort to solve the MK instances with and without the inclusion of merged cover inequalities. CPLEX 12.5 [44] solves all of the instances at default settings, but writing node files out to memory is used for the larger instances. All results are obtained using a PC with an i7-4770 processor at 3.4 GHz with 8 GB of RAM.
3.1. Computational Results
The computational study considered the variations of each implementation strategy by testing both small and large instances. Solving all 10 smaller instances required from 10 to 15 minutes. Solving all 10 larger instances typically needed 1 to 2 days. Instead of reporting the time in seconds, the data below compares computational ticks in CPLEX, as this is more accurate. It should be noted that the time in seconds was highly correlated to ticks. The overall improvement in time was plus or minus two percent of the percent improvement in ticks.
Ticks provide a more accurate comparison between the experimental runs because the computational time in seconds is subject to variability on different computers. Fischetti, et al. argue the benefit of using ticks in [45] . Ju, et al. use a similar process to report their computational results [46] . Since the two categories of MK test problems included 10 multiple knapsack subordinate instances, most of the tables compare the aggregate total ticks required to solve all 10 problems using the baseline CPLEX 12.5 and the inequality merging technique.
3.1.1. Computation Results for Smaller Problems
Problems from the smaller MK instances (file mknapcb2) offered an excellent opportunity for extensive experimentation with each of the implementation strategies. Table 2 and Table 3 show the best known results
![]()
Table 2. Changing implementation strategies for smaller MK problems, 1 - 3 Cuts.
![]()
Table 3. Changing implementation strategies for smaller MK problems, 4 - 5 Cuts.
from these experiments on the smaller MK instances. Since there are 5 rows in the smaller test problems, each implementation strategy was tested with the inclusion of 1 - 5 merged inequalities. Table 2 shows the results for iterations with 1, 2, or 3 merged inequalities added. Table 3 shows the results with 4 or 5 merged inequalities added.
Observe that inequality merging outperformed the baseline CPLEX computational ticks for all strategies in Table 2 with 1, 2, or 3 added inequalities, and inequality merging also outperformed the baseline CPLEX by about 9% on average. The 4 and 5 cut strategies from Table 3 outperformed baseline CPLEX by about 4%. This demonstrates that adding more merged inequalities creates diminishing returns because of additional com- putational requirements as the A matrix and basis grow in size. Preferred implementation strategies should focus on including 1, 2, or 3 merged cutting planes.
Table 4 aggregates results from Table 2 and Table 3, and it reports the average results based upon different pseudo-costing strategies. Observe that many of the experimental runs in Table 2 and Table 3 included a pure strategy (all reduced costs, all a values, or all balanced cuts). However, some of the experimental runs include a mixture of strategies such as the 3 cut scenario with 1 cut of each pseudo-costing strategy. Experiments of this type are listed under “Mixture of Strategies” in Table 4. Notice that each of the three pure strategies performed well, at about the same level of improvement. However, there may be some additional benefit to mixing pseudo- cost strategies if multiple merged inequalities are generated.
Merged inequalities almost always improved the computational time, regardless of the overlapping strategy. It appears that deliberate overlapping of rows provides even stronger results if multiple cutting planes are added. This is consistent with the theory motivating Theorem 3. Overlapping allows the algorithm to search in rows that had previously been used to generate a host cover inequality for an earlier merged cut. If DCSA is employed, the algorithm may also search all candidate rows including those that had previously generated a host inequality. Thus, all future experimentation overlaps rows.
3.1.2. Computational Results for Larger Problems
As the problems increased in size, the computational time quickly increased. The same implementation strategies tended to yield the strongest results with larger problems, as shown in this section. Solving all 10 MK instances required from 1 to 2 days to solve. Table 5 shows the best known results for the large MK problems when the recommended implementation strategies are followed.
Table 5 shows that inequality merging continues to provide an average improvement of about 9% over the baseline CPLEX computational effort even on challenging instances. This is roughly the same level of average improvement observed in the smaller MK instances. Notice that following the recommended implementation strategies always improved the solution times. This provides strong evidence that inequality merging is a beneficial technique for MK problems, and the reduction of computational ticks correlates to hours of time savings for large problems.
Clearly a focus on reduced costs had the best impact for this particular grouping of larger MK instances, but that may not be the case in general. Previous analysis from Table 4 suggested that different pseudo-costing techniques may be preferred for particular problems, but focusing on reduced costs was actually the least preferred in that grouping of smaller MK instances. Identifying the reason that certain methods dominate other pseudo-costing techniques in particular problems is an excellent area for future research.
Table 6 shows the best solution times for each of the 10 MK instances in the larger files. In addition, the table also describes the implementation strategy that yields the best result for each problem. Merging improved the solution times for each of the 10 problems, with an average reduction of computational requirements by 25.8%. However, the best single result for each sub-problem came from a wide variety of implementation strategies. These include instances that search all donor rows with DCSA and other instances that consider only specified randomly-selected donor inequalities that define single overlaps. The two best results include both overlapping strategies and DCSA facilitated the single best percentage improvement in problem 1. It is clear that each strategy yields strong results in specific instances, and neither overlapping strategy dominates the other.
![]()
Table 4. Average ticks of pseudo-costing strategies from Table 2 and Table 3.
![]()
Table 5. Changing implementation strategies for larger MK problems, 1 - 3 Cuts.
![]()
Table 6. Best merging performance by problem for ![]() and
and![]() .
.
These larger problems are excellent representatives of difficult, real-world problems. Thus, the observed reductions in computational requirements validated the theoretical advancements in this research as effective methods to help decrease computational effort for modern MK problems.
4. Conclusion and Future Work
This paper provides the theoretical foundations needed to build merged cover inequalities in MK instances. The theorems generate conditions for validity, using the ![]() term to identify candidate merging indices and simultaneously merging on all rows. Two algorithms support the newly-discovered theory, including an algorithm to reduce the size of
term to identify candidate merging indices and simultaneously merging on all rows. Two algorithms support the newly-discovered theory, including an algorithm to reduce the size of ![]() and a second algorithm to find the strongest coefficients for each candidate index during simultaneous merging.
and a second algorithm to find the strongest coefficients for each candidate index during simultaneous merging.
The computational study validates inequality merging as an effective technique that reduces computational time for multiple knapsack problems. Preferred implementation strategies should generate 1, 2, or 3 cuts and overlap the rows. These strategies provide the strongest results, yielding an average reduction of computational effort by about 9%. The computational study provides strong evidence that inequality merging yields productive cutting planes for MK problems, and it is likely that similar computational improvements will be achieved for other IPs.
Three ideas present themselves as excellent candidates for future research extensions. In this paper, inequality merging occurs on a single variable. The theory may be extended to merge on multiple variables. Since this paper focuses on cover inequalities and MK instances, another theoretical extension may merge other classes of cutting planes in general IPs.
All of the computational analysis in this research was performed on the first 10 problems of each file provided by Chu and Beasley [42] with a tightness ratio of 0.25. Other test problems exist in the same files with different tightness ratios, and future research should consider if varying tightness ratios tend to motivate different levels of computational improvement when merged cover inequalities are added to the MK instance.