Robust Inference for Time-Varying Coefficient Models with Longitudinal Data ()
Received 28 September 2015; accepted 14 December 2015; published 17 December 2015


1. Introduction
The defining characteristic of a longitudinal data study is that individuals are measured repeatedly over a given time period, longitudinal studies are in contrast to cross-sectional studies, in which a single outcome is measured for each individual. The repeated measurements within each subject are generally correlated with each other, but different individuals can be assumed to be independent. The primary advantage of a longitudinal study is its effectiveness for studying changes over time. Statistical research in this field has been very active, and many parametric models have been developed. See Diggle et al. [1] , Davidian and Giltinan [2] , Vonesh and Chinchilli [3] , and the references therein.
As overwhelming longitudinal data exist in biomedical studies, there are increasing demands for a generally applicable inference tool for analysing these datasets. The parametric models are efficient for analysing longitudinal data but may suffer from mis-specification. To reduce possible modeling bias, different nonparametric and semiparametric methods have been studied in the literature, for example Zeger and Diggle [4] , Müller [5] , Eubank et al. [6] , He et al. [7] [8] , among others. In particular, a useful nonparametric model for analysing time-varying effects of covariates receives much attention. Examples include Hoover et al. [9] , Fan and Zhang [10] , Huang et al. [11] and others. These works focus on the least-squares based estimation. While they are useful in some applications, the shortcoming for lack of robustness is naturally raised. This motivates us to consider a robust inference tool for the time-varying coefficient models.
In this paper, we consider a local M-estimation approach based on local polynomial smoother and a robustified “generalized likelihood ratio (GLR)” statistic to test if parts of the coefficients are constants or of certain parametric forms. This in particular allows one to nonparametrically check the goodness-of-fit of the usual linear models widely used in practice (see for example Diggle et al. [1] ). We conduct extensive simulations to demonstrate that the proposed estimation method is robust against outliers and error distributions, and that the robustified GLR tests are powerful than its counterpart when the error deviates away from normality.
This paper is organized as follows. In section 2, the local M-estimation approach is introduced; a data-driven bandwidth selection rule is also given. In Section 3, we focus on the robustified GLR tests. Simulations are conducted in Section 4, where the performances of the different tests are compared, and a real example is also used to illustrate the proposed method. Finally, the paper is concluded by a discussion.
2. Model and Estimation
2.1. Local M-Estimation
Consider the following time-varying coefficient model,
 (1)
(1)
where 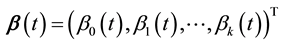 for
for 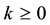 and
and 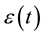 is a zero-mean correlated stochastic process that cannot be explained by the covariates
is a zero-mean correlated stochastic process that cannot be explained by the covariates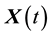 . As in Hoover et al. [9] we regard the repeated observations
. As in Hoover et al. [9] we regard the repeated observations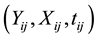 , for
, for  and
and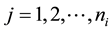 , as a random sample from model (1), that is,
, as a random sample from model (1), that is,
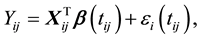 (2)
(2)
where 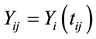 is the observed response,
is the observed response, 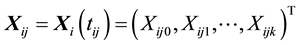 is the observed covariates for the ith subject at time
is the observed covariates for the ith subject at time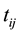 , and
, and  is a zero-mean stochastic process with covariance function
is a zero-mean stochastic process with covariance function 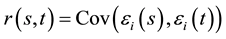 . For this model, we assume that the measurements on the responses for different subjects are independent, but
. For this model, we assume that the measurements on the responses for different subjects are independent, but 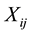 may be correlated at different time points within each subject,
may be correlated at different time points within each subject,![]() ’s are also independent for different subjects. Model (1) or (2) is a useful extension to the usual linear model for longitudinal/panel data analysis in Lindsey [12] , Jones [13] , Diggle, et al. [1] , Hand and Crower [14] , among others.
’s are also independent for different subjects. Model (1) or (2) is a useful extension to the usual linear model for longitudinal/panel data analysis in Lindsey [12] , Jones [13] , Diggle, et al. [1] , Hand and Crower [14] , among others.
There are several methods for estimating the coefficient![]() , for example, the smoothing spline method in Brumback and Rice [15] , Hoover et al. [9] , and Chiang et al. [16] , the kernel smoother in Hoover et al. [9] , Wu et al. [17] , Wu and Chiang [18] , and Chiang et al. [16] , and other methods such as the two-step estimation in Fan and Zhang [10] and the global smoothing procedure using basis function approximations in Huang et al. [11] . These methods are all based on the least squares principle and suffer from the shortcoming of non-robustness. It is worthy of developing a robust estimation and testing method for the model (1). Generally speaking, one can develop different testing methods for different estimating approaches. To introduce our method, we begin with the local polynomial estimation (see Hoover et al. [9] ), that is, to find
, for example, the smoothing spline method in Brumback and Rice [15] , Hoover et al. [9] , and Chiang et al. [16] , the kernel smoother in Hoover et al. [9] , Wu et al. [17] , Wu and Chiang [18] , and Chiang et al. [16] , and other methods such as the two-step estimation in Fan and Zhang [10] and the global smoothing procedure using basis function approximations in Huang et al. [11] . These methods are all based on the least squares principle and suffer from the shortcoming of non-robustness. It is worthy of developing a robust estimation and testing method for the model (1). Generally speaking, one can develop different testing methods for different estimating approaches. To introduce our method, we begin with the local polynomial estimation (see Hoover et al. [9] ), that is, to find![]() ’s to minimize
’s to minimize
![]() (3)
(3)
where![]() , and d denotes the order of the polynomial used in smoothing.
, and d denotes the order of the polynomial used in smoothing.
The above local least squares based estimation is not robust against outliers and heavy tailed errors. To fix this problem, we propose to estimate the coefficient function by minimizing
![]() (4)
(4)
where ![]() is an outlier resistant function. The coefficient functions
is an outlier resistant function. The coefficient functions![]() ’s is estimated by
’s is estimated by![]() ’s
’s![]() , the solutions of the above optimization problem. The resulting estimators are so-called the local M-type estimator of
, the solutions of the above optimization problem. The resulting estimators are so-called the local M-type estimator of![]() . If
. If ![]() has a derivative
has a derivative![]() , then the solutions of (4) solve the following equations:
, then the solutions of (4) solve the following equations:
![]() (5)
(5)
for ![]() and
and![]() .
.
The above method is in the same spirit of the local M-estimation studied for cross-sectional data in Fan and Jiang [19] and Jiang and Mack [20] . It can be shown that the estimator is ![]() -consistent under certain conditions. The estimator involves a selection of the outlier resistant function. Much work in the literature has demonstrated that the Huber’s
-consistent under certain conditions. The estimator involves a selection of the outlier resistant function. Much work in the literature has demonstrated that the Huber’s ![]() -class, i.e.,
-class, i.e., ![]() , is satisfactory for robust estimation in the location model and nonparametric regression (Huber [21] ; Jiang and Mack [20] ), where a method for determining the parameter k was studied in Jiang and Mack [20] . However, our experience shows that a rule of thumb for the choice of k, such as
, is satisfactory for robust estimation in the location model and nonparametric regression (Huber [21] ; Jiang and Mack [20] ), where a method for determining the parameter k was studied in Jiang and Mack [20] . However, our experience shows that a rule of thumb for the choice of k, such as ![]() where s is the robust standard deviation of the residuals (Serfling [22] ), is simple and satisfactory in the present situation. Other choices of the outlier resistant function are also possible, such as
where s is the robust standard deviation of the residuals (Serfling [22] ), is simple and satisfactory in the present situation. Other choices of the outlier resistant function are also possible, such as ![]() which leads to the least absolute deviation estimation (Jiang et al., [23] ).
which leads to the least absolute deviation estimation (Jiang et al., [23] ).
The Newton algorithm can be used to find the solutions to the Equations (5). If the initial values of the parameters for iteration are good enough, for example, from the least squares estimation, then the iterative solutions can be found in a few steps, which is theoretically verified in Jiang and Mack [20] ) for nonparametrically modeling dependent data. In our simulations, the least squares based estimators in (2) will be employed as the initial values.
2.2. Bandwidth Selection
The performance of the estimator in (4) depends on the smoothing parameter h. There are several approaches to the selection of the bandwidth, such as the cross-validation (CV) and generalized cross-validation (GCV) criteria in Hastie and Tibshirani [24] . We here extend the CV method to the present situation for determining the bandwidth h. Specifically, denote by ![]() the solution of (4) or (5) based on all the observations without the measurements for ith subject. Then the bandwidth h can be estimated by the minimizer
the solution of (4) or (5) based on all the observations without the measurements for ith subject. Then the bandwidth h can be estimated by the minimizer ![]() of
of
![]() (6)
(6)
where![]() .
.
The minimization of (6) is time-consuming for simulations, even though it is not for real data analysis. We here suggest a pre-determination of ![]() before simulations. Specifically, the procedure is detailed as follows:
before simulations. Specifically, the procedure is detailed as follows:
1) Generate several samples (20 for instance) from (2), then minimize (6) to get the ![]() for each sample
for each sample
and compute the average ![]() of the
of the![]() ’s;
’s;
2) Fix the bandwidth ![]() in each simulation to find the estimator in (4).
in each simulation to find the estimator in (4).
In step 1), the computational burden can be further reduced if one uses an easy-evaluated bandwidth as initial value, such as the one from the GCV criterion for the local least squares based estimator. Since the estimated bandwidths for the local least squares estimation and the local M-estimation are highly correlated in general, the minimization of ![]() will be achieved in a few iterations.
will be achieved in a few iterations.
3. Robustified GLR Tests
For simplicity, consider the following testing problem
![]() (7)
(7)
where![]() , and
, and ![]() is an unspecified constant vector. Let
is an unspecified constant vector. Let
![]()
![]()
where![]() ’s are the usual M-estimators of the coefficients under
’s are the usual M-estimators of the coefficients under![]() , and
, and![]() ’s are the local M-estimators of the coefficient functions under
’s are the local M-estimators of the coefficient functions under![]() . Define the following testing statistic for the testing problem (7):
. Define the following testing statistic for the testing problem (7):
![]() (8)
(8)
Intuitively, large values of ![]() provide evidences against
provide evidences against![]() . The proposed statistic is basically based on the comparison of residuals between the null and the alternative. It can be regarded as a robustification for the GLR testing statistic studied in Fan et al. [25] , Fan and Huang [26] , and Fan and Jiang ([27] [28] ). In particular, if
. The proposed statistic is basically based on the comparison of residuals between the null and the alternative. It can be regarded as a robustification for the GLR testing statistic studied in Fan et al. [25] , Fan and Huang [26] , and Fan and Jiang ([27] [28] ). In particular, if ![]() is employed, then
is employed, then ![]() is in the same formulas as those in the afore-mentioned papers. For the errors departing away from normality, one can expect the
is in the same formulas as those in the afore-mentioned papers. For the errors departing away from normality, one can expect the ![]() to be robust and more powerful than its local least-squares counterpart with
to be robust and more powerful than its local least-squares counterpart with![]() . For more general testing problems such as
. For more general testing problems such as ![]() for
for![]() , which tests whether
, which tests whether ![]() admits a certain parametric form, the above testing statistic can be similarly
admits a certain parametric form, the above testing statistic can be similarly
constructed if one replaces the ![]() with the local M-estimator under
with the local M-estimator under![]() .
.
Bootstrap Estimate of Null Distribution
To implement the robustified GLR tests, one needs to obtain the null distribution of ![]() under
under![]() . In the following, we use simulations to compute the null distribution of the test statistic for a finite sample. It can be applied to both the local least squares and the local M-estimation methods. The computational algorithm is given as follows. For an easy illustration, we first consider the situation with
. In the following, we use simulations to compute the null distribution of the test statistic for a finite sample. It can be applied to both the local least squares and the local M-estimation methods. The computational algorithm is given as follows. For an easy illustration, we first consider the situation with![]() .
.
1) Obtain the nonparametric estimate ![]() along with its associated bandwidth
along with its associated bandwidth![]() .
.
2) Compute the testing statistic ![]() and the residual vectors
and the residual vectors ![]() under the alternative, for
under the alternative, for![]() .
.
3) For each given![]() , draw a bootstrap residual vectors
, draw a bootstrap residual vectors ![]() from the centered empirical distribution of
from the centered empirical distribution of ![]() and compute
and compute![]() .
.
4) Use the generated random sample ![]() (
(![]() ;
;![]() ) and the bandwidth
) and the bandwidth ![]() to calculate the value
to calculate the value ![]() of the robustified GLR testing statistic.
of the robustified GLR testing statistic.
5) Repeat steps 3 and 4 B times to obtain the bootstrap statistics![]() .
.
6) The P-value of the testing statistic ![]() is the percentage of the bootstrap statistics
is the percentage of the bootstrap statistics ![]() that exceed
that exceed![]() .
.
Similar simulation approaches to determining the p-value of a testing statistic were given in Fan and Jiang [27] for additive models and Hui and Jiang [29] for DTARCH models. For the case that![]() ’s are not equal, the conditional bootstrap method is infeasible, but one can use a resampling subject bootstrap method (see for example
’s are not equal, the conditional bootstrap method is infeasible, but one can use a resampling subject bootstrap method (see for example
Huang, Wu and Zhou, [11] ) to replace the bootstrap method above. Specifically, let ![]() be generated as follows:
be generated as follows:
![]()
where ![]() is the estimate under
is the estimate under ![]() and
and![]() ’s are the residuals from the null model. Resample n subjects with
’s are the residuals from the null model. Resample n subjects with
replacement from ![]() to obtain a bootstrap sample
to obtain a bootstrap sample
![]() . Let
. Let ![]() be the value of the testing statistic for the bootstrap sample. With B independent replications, we obtains B bootstrap estimators
be the value of the testing statistic for the bootstrap sample. With B independent replications, we obtains B bootstrap estimators![]() . Then p-value of the testing statistic
. Then p-value of the testing statistic
![]() can be obtained as in step 6 above.
can be obtained as in step 6 above.
4. Numerical Studies
4.1. Robustness of the Estimation
In this section, we compare the performance of the local M-estimation with the local least squares estimation. For the outlier-resistant function, we opt for the Huber ![]() -functions in our numerical study:
-functions in our numerical study:
![]()
The rule of thumb in Section 2.1 for the choice of k will be employed.
Example 1. Consider the following model,
![]() (9)
(9)
where![]() ,
, ![]() ,
, ![]() and
and ![]() are respectively from
are respectively from ![]() models in such a way that
models in such a way that![]() ,
, ![]() ,
, ![]() , and
, and![]() . For simplicity, we used the time points
. For simplicity, we used the time points ![]() which are equally spaced for each i. The errors
which are equally spaced for each i. The errors ![]() are iid for all i and j. We considered the following four distributions for the errors:
are iid for all i and j. We considered the following four distributions for the errors:
(A1)![]() ;
;
(A2)![]() ;
;
(A3)![]() ;
;
(A4)![]() .
.
We simulated 200 samples of size ![]() and
and ![]() from the model (9). The averages of
from the model (9). The averages of ![]() and the 2.5% and 97.5% sample quantiles of
and the 2.5% and 97.5% sample quantiles of ![]() among simulations were calculated at each time points. In addition, we also computed the mean absolute deviation error (MADE) of the estimators at the time points (for
among simulations were calculated at each time points. In addition, we also computed the mean absolute deviation error (MADE) of the estimators at the time points (for![]() ),
),
![]()
The average of values of the above MADE over simulations was calculated and reported in Table 1 for the error models (A1) and (A3). The results show that the local LS estimator and the local M-estimators have similar accuracy if the error is normal, but the latter performs better than the former if the error deviates away from normality. We display in Figure 1 the estimators of the coefficient functions along with the widths of the envelopes formed by pointwise 2.5% and 97.5% quantiles of the estimators among simulations, where ![]() is easier to estimate than
is easier to estimate than ![]() and the estimated envelopes’ widths for
and the estimated envelopes’ widths for ![]() are not reported for saving space. It is evident that both the local LS estimator and the local M-estimator have little biases, and the latter is much better than the former in terms of the envelopes’ widths when the error deviates away from the normal distribution.
are not reported for saving space. It is evident that both the local LS estimator and the local M-estimator have little biases, and the latter is much better than the former in terms of the envelopes’ widths when the error deviates away from the normal distribution.
We did simulations with the error distributions in (A2) and (A4). The results are similar and omitted for saving space.
![]()
Table 1. MADEs under the errors (A1) and (A3) for Example 1.
![]()
Figure 1. Estimated curves and widths of envelopes. Upper panel: results for the error in (A1); lower panel: results for the error in (A2). (a) and (c): the average of estimated curves; solid―true curves, dash-dotted―local LS estimator, dashed―local M-estimator. (b) and (d): pointwise widths of envelopes for![]() , which were formed by the pointwise 2.5% & 97.5% quantiles of the estimators among simulations; solid―local LS estimator, dashed―local M-estimator.
, which were formed by the pointwise 2.5% & 97.5% quantiles of the estimators among simulations; solid―local LS estimator, dashed―local M-estimator.
Example 2. In this example, we consider the model (9) with much more complex structures for the covariates, the errors, and the coefficient functions than those in Example 1. Different from Example 1, the two co-
variates are now correlated, and the error ![]() are correlated within subjects. Specifically,
are correlated within subjects. Specifically, ![]() ,
, ![]() ,
, ![]() and
and ![]() are from the following two-dimensional AR model,
are from the following two-dimensional AR model,
![]()
where ![]() and
and![]() . We used the same
. We used the same![]() ’s as in Example 1. The errors
’s as in Example 1. The errors ![]() are iid for all different subjects but may be correlated within subjects, which were generated from the following three distributions:
are iid for all different subjects but may be correlated within subjects, which were generated from the following three distributions:
(B1)![]() ;
;
(B2)![]() , where
, where![]() ;
;
(B3)![]() , where
, where![]() .
.
We conducted 400 simulations. In each simulation, a samples of size ![]() and
and ![]() was drawn. We calculated the estimators along with the related MADEs and envelopes. Table 2 reports the MADEs for the estimated coefficient functions. It is evidenced that the local M-estimator is better than its counterpart under the heavy tailed error in (B3). Both estimators have similar MADEs under the other two errors in (B1) and (B2).
was drawn. We calculated the estimators along with the related MADEs and envelopes. Table 2 reports the MADEs for the estimated coefficient functions. It is evidenced that the local M-estimator is better than its counterpart under the heavy tailed error in (B3). Both estimators have similar MADEs under the other two errors in (B1) and (B2).
Since ![]() is much simpler than
is much simpler than![]() , we now consider only the the estimated curves for
, we now consider only the the estimated curves for![]() . Figure 2 displays the estimated curves for
. Figure 2 displays the estimated curves for ![]() along with the 95% confidence intervals under the error (B2), and the widths of the envelopes for
along with the 95% confidence intervals under the error (B2), and the widths of the envelopes for ![]() under the errors in (B2) and (B3). The average of the estimator in Figure 2(a) and the corresponding 95% confidence intervals in Figure 2(b) show that the local M-estimator well captures the structure of the true curve
under the errors in (B2) and (B3). The average of the estimator in Figure 2(a) and the corresponding 95% confidence intervals in Figure 2(b) show that the local M-estimator well captures the structure of the true curve![]() . It is seen from Figure 2(c) and Figure 2(d) that the local M-estimator is better than the local LS estimator when the error deviates away from the norm distribution.
. It is seen from Figure 2(c) and Figure 2(d) that the local M-estimator is better than the local LS estimator when the error deviates away from the norm distribution.
4.2. Null Distribution and Power of Test
In this section, we conduct simulations to show that our conditional bootstrap method gives a good estimate of the null distribution, and to compare the powers of different nonparametric tests.
Example 3. To compare the powers of different tests, we consider the testing problem (7) for the model (9). The null model is the constant-coefficient model with![]() ,
, ![]() ,
, ![]() and
and ![]() are the same as in Example 1. The error
are the same as in Example 1. The error ![]() is generated from one of the following distributions:
is generated from one of the following distributions:
(C1)![]() ;
;
(C2)![]() ;
;
(C3)![]() .
.
We use a sequence of alternative models, ![]() , to calculate the powers of the tests.
, to calculate the powers of the tests.
We conducted 400 simulations. The sample size is the same as in Example 1. The bootstrap replicates number is![]() . Figure 3 displays the histograms and the estimated probability densities of the testing statistic based on the common kernel method under the null model. It is seen that the null distributions of the testing statistics are very close, which shows that in finite samples the two tests hold close levels and hence have approx-
. Figure 3 displays the histograms and the estimated probability densities of the testing statistic based on the common kernel method under the null model. It is seen that the null distributions of the testing statistics are very close, which shows that in finite samples the two tests hold close levels and hence have approx-
![]()
Figure 2. Estimated curves and envelopes. Upper panel: estimated curves for ![]() along with its 95% confidence intervals based on the local M-estimation; solid―true curve, dashed―estimated curves. Lower panel: widths of envelopes formed by 2.5% and 97.5% sample quantiles among simulations, solid―for local LS estimator, dashed―for local M-estimator. (a) (b) (d): the results under the error in (B2); (c): the results under the error in (B3).
along with its 95% confidence intervals based on the local M-estimation; solid―true curve, dashed―estimated curves. Lower panel: widths of envelopes formed by 2.5% and 97.5% sample quantiles among simulations, solid―for local LS estimator, dashed―for local M-estimator. (a) (b) (d): the results under the error in (B2); (c): the results under the error in (B3).
![]()
Figure 3. Histograms and estimated probability densities of TN’s. Left panel: based on the local LS-estimator; right panel: based on the local M-estimator with Huber ![]() -function. (a) (b): results under the error in (C1); (c) (d): results under the error in (C2); (e) (f): results under the error in (C3).
-function. (a) (b): results under the error in (C1); (c) (d): results under the error in (C2); (e) (f): results under the error in (C3).
imately equal type I errors. Figure 4 shows the powers of the tests based on the local LS and local M-estimators. It demonstrates that the proposed test is more powerful than that based on local LS-estimator when the error deviates away from the normal distribution. Both tests are approximately the same powerful under the normal error.
4.3. A Real Example
We here illustrate how to use the proposed method in practice. Consider the body-weight of male Wistar rats dataset in Brunner et al. ([30] , Table A11). For this dataset, the objective of the experience is to assess the toxicity of a drug on the body-weight evolution of Wistar rats. A group of ten rats was given a placebo, while a second group of ten was given a high dose of the drug. For each rat in the study, its body-weight was observed once a week over a period of 22 weeks. Figure 5(a) and Figure 5(b) displays the data curves for the two groups.
To check if the body-weights of the two test groups differ in their evolution over time, Brunner et al. [2] compared the time curves of the mean body-weights for both groups, and evaluated the ANOVA-type statistics. Their results do not support the conjecture of different body-weight evolutions in the two groups.
We are interested in investigating the conjecture. Since Figure 5(a) and Figure 5(b) exhibit the time-varying feature of the body-weights of rats, it seems reasonable to model the dataset via the following time-varying coefficient model:
![]() (4.10)
(4.10)
where ![]() equals 1 if in the treatment group and equals 0 if in the control group. Then
equals 1 if in the treatment group and equals 0 if in the control group. Then ![]() reflects the evolution of average body-weight for the control group, and
reflects the evolution of average body-weight for the control group, and ![]() reflects that for the treatment group.
reflects that for the treatment group.
Since in the beginning the average body-weight of the rats in the placebo group is bigger than that in the
![]()
Figure 4. Powers of TN’s. Left panel: powers under significance level 95%; right panel: powers under significance level 90%. (a) (b): results under the error in (C1); (c) (d): results under the error in (C2); (e) (f): results under the error in (C3). Solid - power based on the local LS-estimator; dash-dotted―power based on the local M-estimator with Huber’s ![]() -function.
-function.
![]()
Figure 5. Data curves and the estimated coefficient functions. Left panel: (a) body-weights for the placebo group; (b) body-weights for treatment group. Right panel: (c) estimated curve for![]() ; (d) estimated curve for
; (d) estimated curve for![]() ; solid―the local LS estimator, dash-dotted―the local M-estimate.
; solid―the local LS estimator, dash-dotted―the local M-estimate.
treatment group, we subtract the average body-weight in each group from the body-weight of each subject. This will make the estimators of the coefficient functions be approximately zeros at the beginning. Figure 5(c) and Figure 5(d) report the estimators of ![]() and
and![]() . It seems that the
. It seems that the ![]() is time-varying but the
is time-varying but the ![]() is not, which plausibly reflects that the drug did not affect the average body-weights of rats.
is not, which plausibly reflects that the drug did not affect the average body-weights of rats.
Now we consider the following two hypothesis testing problems:
1)![]() , where
, where ![]() is an unknown parameter vector. This is used to test if the average body-weights of rats evolve over time.
is an unknown parameter vector. This is used to test if the average body-weights of rats evolve over time.
2)![]() . This checks if the drug affects the average body-weights of rats in study.
. This checks if the drug affects the average body-weights of rats in study.
We used ![]() bootstrap replicates for computing the null distributions of the testing statistics. For
bootstrap replicates for computing the null distributions of the testing statistics. For![]() , the P-values are 0.0117 and 0.005 respectively for the local LS-estimation based test and the local M-estimation based test. It seems that the null hypothesis does not hold, which means that the average body-weight of rats for each group changes over time. For
, the P-values are 0.0117 and 0.005 respectively for the local LS-estimation based test and the local M-estimation based test. It seems that the null hypothesis does not hold, which means that the average body-weight of rats for each group changes over time. For![]() , the P-values are 0.9633 and 0.8833 for the tests respectively based on the local LS and local M-estimation methods. This evidences that for the dataset the drug has no effect on the average body-weights of rats. This is consistent to the result of Brunner et al. [30] .
, the P-values are 0.9633 and 0.8833 for the tests respectively based on the local LS and local M-estimation methods. This evidences that for the dataset the drug has no effect on the average body-weights of rats. This is consistent to the result of Brunner et al. [30] .
5. Discussion
We have introduced a robust inference method based on the local M-estimation method and the robustified GLR test. It is demonstrated that the local M-estimators are robust against outliers and error distributions, and the proposed robustified GLR test is more powerful than its counterpart (the GLR test) under certain situations with heavy tailed errors, while both of them perform well under the normal error. The proposed inference approach seems appealing in robustly modeling longitudinal data.
Our method is also applicable to other estimating methods, such as the global smoothing one in Huang et al. [11] , but will not be discussed further.
Acknowledgements
We thank the Editor and the referee for their comments. Supported in part by the NSFC grant 71361010 and by funds provided by the University of North Carolina at Charlotte. Correspondence should be addressed to Jiancheng Jiang at University of North Carolina at Charlotte, USA (E-mail: jjiang1@unc.edu).