Received 2 October 2015; accepted 14 December 2015; published 17 December 2015

1. Introduction
The linear regression model is one of the oldest and most commonly used models in the statistical literature and it is widely used in a variety of disciplines ranging from medicine and genetics to econometrics, marketing, social sciences and psychology. Moreover, the relations of the linear regression model to other commonly used methods such as the t-test, the Analysis of Variance (ANOVA) and the Analysis of Covariance (ANCOVA) [1] [2] , as well as the role played by the multivariate normal distribution in multivariate statistics, place the linear model in the centre of interest in many fields of statistics.
In several applications, expressions for estimates of various parameters of the multiple regression models in terms of the summary statistics are needed. This is more evident in the general area of research synthesis methods, in which a researcher seeks to combine multiple sources of evidence across studies. For instance, in meta- analysis of regression coefficients [3] , which is a special case of multivariate meta-analysis [4] [5] , one is interested in the covariance matrix of the coefficients obtained in various studies, in order to perform a multivariate meta-analysis that takes properly into account the correlations among the estimates. The synthesis of regression coefficients has received increased attention in recent years [3] . This growing interest is probably related to the increasing complexity of the models investigated in primary research, and this seems to be the case for both biological [6] [7] as well as social sciences [8] -[11] . However, as Becker and Wu point out in their work: “the covariance matrix among the slopes in primary studies is rarely reported (though matrices of correlations among predictors are sometimes reported)” [3] . A well-known result from linear regression theory suggests that the covariance matrix of the coefficients depends on the cross-product matrix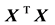 , where
, where 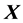 is the design matrix of the independent variables. Thus, in such a case, one needs to have access to individual data, something which is difficult and time-consuming.
is the design matrix of the independent variables. Thus, in such a case, one needs to have access to individual data, something which is difficult and time-consuming.
Another example is the case of the so-called “synthesis analysis”, the aim of which is to combine in a single predictive model information from different variables. Synthesis analysis differs from traditional meta-analysis, since we are not synthesizing similar outcomes across different studies, but instead, we are trying to construct a multivariate model from pairwise associations, or to update a previously created model using external information (i.e. for an additional variable). For example, let’s consider the case of a multiple linear regression model that
relates the de-pendent variable, y, with p independent variables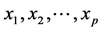 . The aim of the method is to build
. The aim of the method is to build
the multivariate model that relates all predictors, however, not the individual data, but rather the information arising from the pairwise relationships among the variables. Samsa and coworkers were the first to provide details of such method. They used the univariate linear regressions of each xi against y and the correlation matrix that describes the linear relationships among the xi’s [12] . However, they did not provide an estimate for the covariance matrix. Later, Zhou and coworkers presented a different version of the method in which they used the univariate linear regressions of each xi against y along with the simple regressions that related each pair of xi’s [13] . Their method was based on solving a linear system of equations and they also described a method for calculating the variance-covariance matrix of the estimated coefficients using the multivariate delta method, utilizing the estimated variance-covariance matrix of the individual regression models. Such methods could be very important for instance for adjusting a previously obtained estimate for a potential confounder, for adjusting the results of a new analysis using estimates from the literature [14] , or for constructing and updating multivariate risk models [15] -[17] .
In this work, we derive an analytic expression for the covariance matrix of the regression coefficients in a multiple linear regression model. In contrast to the well-known expressions which make use of the cross-product matrix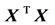 , we express the covariance matrix of the regression coefficients directly in terms of covariance matrix of the explanatory variables. This is very important since the covariance matrix of the explanatory variables can be easily obtained, or even imputed using data from the literature, without requiring access to individual data. In the following, in the Methods section we first present the details of synthesis analysis (2.1) and meta-analysis (2.2), in order to establish notation. Then, in Section (2.3) we present the classical framework of the multivariate normal model on which the problem is based and we give some results concerning some previously published estimators. Afterwards, in Section (2.4) we present the main result consisting of the analytical expression for the covariance of the regression coefficients. Finally, in Section (3) the method is applied to a real dataset, both in a meta-analysis and a synthesis analysis framework. Source code that implements the method, as well as the derivations of the main results are given in Appendix.
, we express the covariance matrix of the regression coefficients directly in terms of covariance matrix of the explanatory variables. This is very important since the covariance matrix of the explanatory variables can be easily obtained, or even imputed using data from the literature, without requiring access to individual data. In the following, in the Methods section we first present the details of synthesis analysis (2.1) and meta-analysis (2.2), in order to establish notation. Then, in Section (2.3) we present the classical framework of the multivariate normal model on which the problem is based and we give some results concerning some previously published estimators. Afterwards, in Section (2.4) we present the main result consisting of the analytical expression for the covariance of the regression coefficients. Finally, in Section (3) the method is applied to a real dataset, both in a meta-analysis and a synthesis analysis framework. Source code that implements the method, as well as the derivations of the main results are given in Appendix.
2. Methods
2.1. Synthesis Analysis
The aim of synthesis analysis is to combine in a single predictive model, information from different variables. For instance, consider the case of a multiple linear regression model that relates the dependent variable, y, with p
independent variables, . The traditional linear regression, models the expectation of y given
. The traditional linear regression, models the expectation of y given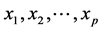 . as a linear combination of the covariates:
. as a linear combination of the covariates:
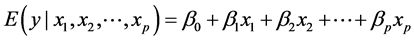 (1)
(1)
The aim of the method is to build the model in Equation (1), in other words, to find the estimates of the pa-
rameters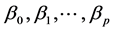 , using however not the individual data, but rather the information arising from the pair-
, using however not the individual data, but rather the information arising from the pair-
wise relationships among the variables. In the following, the regression coefficients are the elements of the (p +
1) × 1 matrix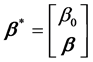 , where
, where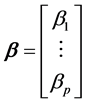 . These relationships could be, from the one hand the univariate linear regressions of each xi against y:
. These relationships could be, from the one hand the univariate linear regressions of each xi against y:
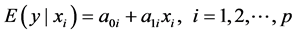 (2)
(2)
On the other hand, we could either have the simple regressions that relate each pair of xi’s:
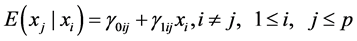 (3)
(3)
or, the correlation matrix that describes the linear relationships among the xi’s:
 (4)
(4)
In Equation (4), the Pearson’s correlation coefficient between xi and xj are denoted by rij for 1 ≤ i, j ≤ p. The first approach for synthesis analysis was presented by Samsa and coworkers [12] who used Equation (2) and Equation (3) in order to calculate the estimates of Equation (1). In particular, the authors used a previously known result that relates 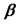 to the matrices A, S, where
to the matrices A, S, where  is the p × 1 matrix of the regression coefficients
is the p × 1 matrix of the regression coefficients
![]() from the multivariate model of Equation (1), A is the p × 1 matrix of the regression coefficients of
from the multivariate model of Equation (1), A is the p × 1 matrix of the regression coefficients of
Equation (2), S is the p × 1 matrix of the standard deviations of the xi covariates and Rx is given by Equation (4). If we denote A and S by:
![]() (5)
(5)
then the regression coefficients can be calculated by:
![]() (6)
(6)
In Equation (6), ![]() stands for the element-wise multiplication (also known as the Hadamard product or dot matrix product) and similarly the division (/) is also element-wise. This method, provides estimates for the re-
stands for the element-wise multiplication (also known as the Hadamard product or dot matrix product) and similarly the division (/) is also element-wise. This method, provides estimates for the re-
gression coefficient![]() , and in order for the intercept, β0, to be calculated, one would need to use the estimated
, and in order for the intercept, β0, to be calculated, one would need to use the estimated ![]() along with the mean values of the variables. Finally, we should mention that the method
along with the mean values of the variables. Finally, we should mention that the method
as described did not provide an estimate for the variance of the coefficients. Thus, construction of confidence intervals and assessment of the statistical significance of the covariates could not be carried out. In a latter work, Zhou and coworkers [13] developed a different method. First, they took expectations on both sides of Equation (1) conditioning on xi:
![]() (7)
(7)
Then, by combining Equation (2), Equation (3) and Equation (7), they obtained the following result:
![]() (8)
(8)
Using now Equation (8), they obtained a system of p equations for the p unknown parameters, which are the p elements of![]() ,
, ![]() , that can be easily solved and p equations for the intercept β0, which however
, that can be easily solved and p equations for the intercept β0, which however
they proved that lead to a unique solution. The authors described also a method for calculating the variance-covariance matrix of the estimated coefficients using the multivariate delta method, utilizing the estimated variance-covariance matrix of the individual regression models (Equation (2) and Equation (3)).
The method is very interesting in that it does not assume normality of the covariates in order to estimate the parameters and thus it is expected to be more robust in case of non-normally distributed variables (but assumes the normality of the estimated parameters in order to use the delta method). On the other hand, the method is quite difficult to be implemented for an arbitrary number of covariates. The system of equations arising from Equation (8) should be solved explicitly and the solution will be more difficult as the number of covariates increases (the authors provided explicit solutions for p = 2 and p = 3). The major difficulty however, lies in the calculation of the covariance matrix with the delta method. The difficulty is particularly evident if we consider that the βi’s are highly non-linear functions of the αi’s and γi’s and thus the partial derivatives require explicit calculations, which are different for different p and can be done only using software that perform symbolic calculations.
2.2. Meta-Analysis of Regression Coefficients
In the meta-analysis of regression coefficients, the problem is different. Here, we have a set ![]() of
of
p regression coefficients arising from k studies (![]() ) and we want to combine them in order to obtain the overall mean
) and we want to combine them in order to obtain the overall mean![]() . Thus, it is a special case of multivariate random-effects meta-analysis [4] [5] ; we denote
. Thus, it is a special case of multivariate random-effects meta-analysis [4] [5] ; we denote
![]() and usually assume that
and usually assume that ![]() is distributed following a multivariate normal distribution around the true means
is distributed following a multivariate normal distribution around the true means![]() , according to the marginal model:
, according to the marginal model:
![]() (9)
(9)
In the above model, we denote by ![]() the within-studies covariance matrix:
the within-studies covariance matrix:
![]() (10)
(10)
and by Ω the between-studies covariance matrix, given by:
![]() (11)
(11)
This is the classic model of multivariate meta-analysis used in several applications [4] [5] [18] . For fitting this model, there are several alternatives, such as Maximum Likelihood (ML), Restricted Maximum Likelihood (REML) or the multivariate method of moments (MM), all of which however require that the diagonal elements of Cs. These are the study-specific estimates of the variance that are assumed known, whereas the off-diagonal elements correspond to the pairwise within-studies covariances, thus for ![]() we have:
we have:
![]() (12)
(12)
On the other hand, the between studies covariance matrix is estimated from the data. Of course, in model of Equation (9) we could also use ![]() and include the intercept as well. However, this will rarely be needed in practical applications where the interest lies in the estimation of covariate effects.
and include the intercept as well. However, this will rarely be needed in practical applications where the interest lies in the estimation of covariate effects.
The major problem in this method, is, as Becker and Wu point out that “in practice, the covariance matrix among the slopes in primary studies is rarely reported (though matrices of correlations among predictors are sometimes reported)” [3] . Usually, ignoring or approximating the within studies covariance matrix produce reliable estimates for the fixed effects parameters but biased estimates for the variance [19] [20] . Thus, ideally one would want to include reliable estimates for the within studies covariances in order to gain the maximum from the multivariate meta-analysis. Currently, since the majority of studies do not report the covariance matrices, a literature-based (i.e. without having access to individual data) meta-analysis would be forced to assume zero correlations between the regression coefficients, limiting this way the efficiency of the method. An alternative, would be to use the model of Riley and coworkers, which, being no-hierarchical, maintains the individual weighting of each study in the analysis but includes only one overall correlation parameter, removing this way the need to know the within-study correlations [21] . For other effect sizes, such as the odds ratio, the relative risk and so on, recent studies have shown that under certain conditions, the correlation can be estimated using only the pairwise correlations of the variables involved [22] [23] . Thus, a similar approach can be followed here concerning the regression coefficients.
2.3. The General Method
We will begin with the multivariate normal model. This is one of the two main approaches for formulating a regression problem (the other one is the approach that assumes that the independent variables are fixed by design). Even though the two approaches are conceptually very different, it is well known that concerning the estimation of the regression parameters (coefficients and their variance), they yield exactly the same results. Consider we
have p + 1 variables, y and ![]() that are distributed according to a multivariate normal distribution. The traditional linear regression, models the expectation of y given
that are distributed according to a multivariate normal distribution. The traditional linear regression, models the expectation of y given ![]() as a linear combination of the covariates
as a linear combination of the covariates ![]() according to Equation (1). If we denote by
according to Equation (1). If we denote by![]() ,
, ![]() and by Σ the
and by Σ the ![]() variance-covariance matrix:
variance-covariance matrix:
![]() (13)
(13)
then we will have ![]() and a well-known result from multivariate statistics allows the arbitrary partitioning of Σ in order to obtain:
and a well-known result from multivariate statistics allows the arbitrary partitioning of Σ in order to obtain:
![]() (14)
(14)
In this case, the partial vectors are once again multivariate normal with![]() ,
, ![]() with Σ11, Σ12, Σ21, and Σ22 being the partial covariance matrices. Then, the conditional distribution of Y1 given Y2 (i.e. the regression of Y2 on Y1) is given by:
with Σ11, Σ12, Σ21, and Σ22 being the partial covariance matrices. Then, the conditional distribution of Y1 given Y2 (i.e. the regression of Y2 on Y1) is given by:
![]() (15)
(15)
If we partition Σ in order to obtain Equation (1), then the partial covariance matrices would be:
![]() (16)
(16)
whereas, Y1 would be a univariate normal![]() . Then, the regression coefficients of Equation (1), with the exception of the intercept, will be given by:
. Then, the regression coefficients of Equation (1), with the exception of the intercept, will be given by:
![]() (17)
(17)
The intercept is given simply as a function of the p regression coefficients and the mean vectors of y and xi’s:
![]()
The covariance matrix of the coefficients in Equation (1) including the intercept is given by:
![]() (18)
(18)
where ![]() denotes the
denotes the ![]() design matrix of the independent variables,
design matrix of the independent variables, ![]() the transpose matrix of
the transpose matrix of ![]() and
and![]() . Notice that
. Notice that![]() , since
, since ![]() is a symmetric matrix and
is a symmetric matrix and ![]() . An alternative estimate for
. An alternative estimate for ![]() in terms of the centralised design matrix
in terms of the centralised design matrix![]() , is discussed in Appendix C.
, is discussed in Appendix C.
In Appendix A, we show that the estimated regression coefficients by this method are identical to the ones obtained by Samsa and coworkers [12] . In other words, we show that:
![]() (19)
(19)
It is obvious that the estimate proposed by Samsa and coworkers [12] is just a re-parameterization of a well-known result and produces identical estimates.
Another commonly used formula, can be derive the estimation of the standardised regression coefficients![]() , for each
, for each![]() , using the correlation matrices
, using the correlation matrices ![]() of Equation (4) and
of Equation (4) and
![]() , where
, where ![]() are the Pearson’s correlation coefficient between
are the Pearson’s correlation coefficient between ![]() and y. Then, the matrix
and y. Then, the matrix ![]() of standardised regression coefficients can be obtained by:
of standardised regression coefficients can be obtained by:
![]() (20)
(20)
The standardised regression coefficients ![]() can be transformed to unstandardised regression coefficients
can be transformed to unstandardised regression coefficients ![]() using
using![]() , or in matrix form
, or in matrix form
![]() (21)
(21)
where ![]() denotes the
denotes the ![]() diagonal matrix such that
diagonal matrix such that![]() . In Appendix B, we show
. In Appendix B, we show
that the coefficients obtained with Equation (20) and Equation (21), are identical to the ones obtained with the use of Equation (6) and Equation (17). That is, we show that:
![]() (22)
(22)
Thus, it is clear that the three methods described above are equivalent and yield identical estimates
![]() (23)
(23)
2.4. Variance-Covariance Matrix
If we want to obtain the variance of the estimated coefficients, we need to turn to Equation (18), which requires explicit knowledge of the ![]() design matrix
design matrix ![]() and the cross-product matrix:
and the cross-product matrix:
![]() (24)
(24)
In synthesis analysis as well as in meta-analysis, one usually does not have access to n × p individual data![]() , and thus, we have to find a method to estimate the variance with information obtained from the published reports. As we already discussed, Samsa and coworkers [12] did not provide an estimate for the covariance matrix, whereas Zhou and coworkers [13] provided a difficult to obtain estimate, using the delta method. However, the variance of a regression coefficient (let’s say βi) can be obtained relatively easily from summary statistics and it can be shown to be equal to:
, and thus, we have to find a method to estimate the variance with information obtained from the published reports. As we already discussed, Samsa and coworkers [12] did not provide an estimate for the covariance matrix, whereas Zhou and coworkers [13] provided a difficult to obtain estimate, using the delta method. However, the variance of a regression coefficient (let’s say βi) can be obtained relatively easily from summary statistics and it can be shown to be equal to:
![]() (25)
(25)
The formula in Equation (25) can be found in many textbooks with the proof traced back in earlier versions of Green’s Econometrics Analysis [24] ; another elegant proof can be found in [25] . Here, ![]() is the squared multiple correlation that relates xi with the rest of the independent variables, whereas σ2 is the total variance of the
is the squared multiple correlation that relates xi with the rest of the independent variables, whereas σ2 is the total variance of the
regression. The term ![]() is usually named “variance inflation factor”. In many applications, we may
is usually named “variance inflation factor”. In many applications, we may
conveniently assume that the total variance remains the same if we add xi in the model, so we may write the variance of the regression coefficient in the full model as a function of the variance of the coefficient in the univariate model of Equation (2):
![]() (26)
(26)
Clearly, in most of the situations this is an upper bound [25] [26] that leads to conservative estimates but it may be useful in many practical applications. In order to evaluate Equation (25), we need to calculate ![]() and σ2. As we already said, σ2 can be obtained from:
and σ2. As we already said, σ2 can be obtained from:
![]() (27)
(27)
We need to remind however, that since this quantity is usually estimated, in real applications we need to adjust it (see [27] pp 405) in order to obtain the unbiased estimator:
![]() (28)
(28)
On the other hand, an easy way (among others) to obtain ![]() is using:
is using:
![]() (29)
(29)
where υii is the i-th diagonal element of![]() .
.
The main result of this work is to provide a closed-form expression for the covariance, that does not include![]() . In Appendix C we show that the covariance is given by:
. In Appendix C we show that the covariance is given by:
![]() (30)
(30)
where ![]() is the ij-partial correlation of xi with xj-controlling for the remaining variables. For
is the ij-partial correlation of xi with xj-controlling for the remaining variables. For![]() , the ij-partial correlation coefficient is defined [28] as:
, the ij-partial correlation coefficient is defined [28] as:
![]() (31)
(31)
with ![]() being the submatrix that is obtained by deleting the i-th row and j-th column of the correlation ma-
being the submatrix that is obtained by deleting the i-th row and j-th column of the correlation ma-
trix ![]() in Equation (4). Moreover, for
in Equation (4). Moreover, for ![]() the already known from Equation (25) variance of
the already known from Equation (25) variance of ![]() is recovered as follows:
is recovered as follows:
![]() (32)
(32)
Interestingly, the correlation between the coefficients will simply be given by:
![]() (33)
(33)
Thus, another useful relation can be obtained if we consider the ![]() diagonal matrix
diagonal matrix ![]() such that
such that![]() , then, it is obvious that
, then, it is obvious that
![]() (34)
(34)
where Pp is the p × p matrix of ij-partial correlations![]() . The variance of the intercept (β0) can be obtained by using the properties of the covariance function, some well known results from linear regression and Equation (25), Equation (30):
. The variance of the intercept (β0) can be obtained by using the properties of the covariance function, some well known results from linear regression and Equation (25), Equation (30):
![]() (35)
(35)
Similarly, we may obtain the covariance of ![]() with
with![]() :
:
![]() (36)
(36)
At this point we should note that Equation (33) was also mentioned by Becker and Wu, and was attributed to [29] . However, the formula was given there only as an unsolved problem for the regression with two independent variables. Most probably, Becker and Wu (since they were aware of the formula), overlooked the fact that the partial correlation coefficient can be calculated from the pairwise correlations, using simple matrix manipulations. To the best of the authors’ knowledge, Equation (30) and its derivation is novel, since it cannot be found or mentioned in any of the traditional books of linear regression or multivariate analysis [24] [27] [29] -[33] .
3. Results and Discussion
As an illustrative example for both meta-analysis and synthesis analysis, we used a publicly available dataset concerning Diabetes in Pima Indians. The dataset has been created from a larger dataset and it was obtained from the UCI Machine Learning Repository [34] (http://archive.ics.uci.edu/ml/datasets/Pima+Indians+Diabetes). The dataset has been used in the past in several applications for constructing prediction models for diabetes [35] . Here, we chose to use plasma glucose concentration at 2 hours in an oral glucose tolerance test as the dependent variable. For predictors, we used the diastolic blood pressure (mm Hg), the triceps skin fold thickness (mm), the 2-hour serum insulin (mu U/ml), the body mass index (weight in kg/(height in m)^2) and the age (years). The code provided in Appendix D, makes clear that the method, using only the summary statistics, produces identical estimates with the standard linear regression analysis on the original data.
Afterwards, we used the same dataset in order to create an “artificial” meta-analysis dataset. We randomly split the dataset in 10 subsets (which we treat as “studies”) of approximate the same number of participants (from 55 to 86). For each dataset, we performed the same calculation and estimated the same model for predicting plasma glucose concentration. The estimates for the regression coefficients and their standard errors in each subset are listed in Table 1. Then, we applied the various alternative methods in a meta-analysis of these 10 “studies”, in order to investigate the effect of the different within-studies covariance matrix.
Firstly, we used the actual within studies covariance matrix obtained from each dataset, which is the ideal but not easily tenable situation. Secondly, we assumed a zero within studies correlation (that is, we used only the variances of the regression coefficients). Thirdly, we applied the alternative method of Riley and coworkers [21] that does not differentiate between and within studies variation (and thus, it requires as input only the variances). And last, we applied the proposed method by assuming a realistic scenario, in which the variances of the regression coefficients are known, but the covariances are not, and thus they are imputed. For all analyses we used the mvmeta command in Stata with the REML option [36] .
By observing the pooled correlation matrix between the independent variables (measured in the combined dataset of 768 individuals), which was found to be equal to:
![]()
Table 1. The estimates of the regression coefficients and their standard errors, after randomly splitting the dataset in 10 subsets (which we treat as “studies”). For each dataset, we performed the same calculation and estimated the same model for predicting plasma glucose concentration. The regression coefficients for each subset (s) correspond to diastolic blood pressure (β1), triceps skin fold thickness (β2), 2-hour serum insulin (β3), body mass index (β4) and age (β5).
![]()
constructed a “working” or “imputed” correlation matrix, equal to:
![]()
This matrix is very simplified, in the sense that large correlations were rounded to 0.25 or 0.5, whereas the smaller ones (which are also the statistically non-significant), were set to zero. In real life applications, such a matrix could have been observed, for instance, in one or more of the included studies, or alternatively, it could have been compiled by collecting pairwise correlations concerning the variables at hand from the literature. Of course, in many applications the obtained matrix would be closer to the actual one, but we deliberately used such a crude approximation in order to simulate a condition in which only vague prior knowledge is available (that is, that two variables are positively correlated or not).
The results of this sensitivity analysis are listed in Table 2. In the table, we also list the results of the regression on the pooled dataset. For reasons of completeness, we also present the results obtained by the so-called meta-analysis of Individual Patients Data (IPD), in which we perform a stratified (by “study”) regression analysis with a linear mixed model with random coefficients for the independent variables [37] .
Even though the interpretation of the results did not change in nearly all analyses, some useful conclusions can be drawn. First of all, four out of the five variables have large and significant effects on glucose (triceps skin fold thickness, insulin, BMI and age) whereas DBP show a negligible (non-significant) association. Most of the methods corroborate to thus, with the exception of the method of Riley which produces a marginally not-significant association for triceps skin fold thickness as well. As expected, the summary meta-analysis using the actual correlation matrix and the meta-analysis using IPD, yield similar even though not identical estimates. Concerning
![]()
Table 2. The estimates for the meta-analysis on k = 10 artificially generated “studies”, obtained using the different methods. The regression coefficients for each subset (s) correspond to diastolic blood pressure (β1), triceps skin fold thickness (β2), 2-hour serum insulin (β3), body mass index (β4) and age (β5). For the explanation of the methods, see the main text.
the other three approaches for summary data meta-analysis, the method that we proposed here, using the “working” correlation matrix, produces the results that resemble closely the ones obtained by using the actual correlation matrix of each “study”. This is true for both the regression estimates and their standard errors. The naive method of assuming zero correlation and the method of Riley, produced slightly biased estimates and standard errors, which especially in the case of Riley’s method yield a non-significant effect for one of the variables (triceps skin fold thickness). This can be explained, since the regression estimates for triceps skin fold thickness β2 had the largest variability between studies and given that the method of Riley cannot differentiate the sources of variability, inflates this way the overall estimate of the variance of the particular coefficient. The dataset and the source code are given at http://www.compgen.org/tools/regression.
The source code that we provide, presents an easily applied and fast method for calculating the covariance matrix of the regression coefficients given the correlation matrix of the explanatory variables. We applied this method in two important problems, namely in the meta-analysis of regression coefficients and in synthesis analysis, with very encouraging results. Since the expression is mathematically equivalent to the already known expressions, when the correlations are the actual correlations of the sample the results are identical. However, even in the case where the actual correlations are not known from the sample, these can be imputed using data from the literature. In this case, as one would expect, the method is very robust to modest deviations from the actual values. Our results, build upon the earlier works of Riley and coworkers and Wu and Becker, and demonstrate the usefulness of the method. Thus, we knew that by ignoring the within studies correlation may result in biased estimates for the variance of the effect size, and that the alternative model may be useful in several circumstances. Now, we have an ever better approximation that can be used in order to obtain better results. The idea of calculating the correlation of estimates using the pairwise correlation of the variablesinvolved, has already being presented in a general meta-analysis setting [22] [23] , and thus, we expect that this method can be useful both to meta-analysis of regression coefficients and to synthesis analysis.
When we reconstruct the correlation matrix using data from the literature, two things need to be addressed. First, we may encounter the problem of a non-positive definite covariance matrix [38] . The chance of this happening increases with the number of variables included and with increasing correlations among them. When two variables are highly correlated (correlation > 0.99), a simple solution would be to exclude one of them from the model. In all other cases, in order to overcome the problem, the most reasonable solution would be to transform the non-positive definite covariance matrix into positive definite. For this, we can use a simple heuristic consisting of adding the negative of the smallest eigenvalue (which will be negative) plus a small constant (10−7) to the diagonal elements of the covariance matrix, or some other among the correction techniques proposed in the literature [38] -[40] . The second thing to remind, is that when we have multiple sources of evidence concerning a particular correlation, or for the whole correlation matrix, then, the obvious solution would be to pool them using appropriate meta-analysis methods. Methods for pooling correlation coefficients are known for years, but it will be advantageous, when possible, to pool the whole correlation matrix using a multivariate technique that properly takes their own covariances into account [41] -[44] .
4. Conclusions
In this work, we derive an analytical expression for the covariance matrix of the regression coefficients in a multiple linear regression model. In contrast to the well-known expressions which make use of the cross-product matrix XTX, we express the covariance matrix of the regression coefficients directly in terms of covariance matrix of the explanatory variables. This is very important since the covariance matrix of the explanatory variables can be easily obtained or imputed using data from the literature, without requiring access to individual data. In particular, we show that the covariance matrix of the regression coefficients can be calculated using the matrix of the partial correlation coefficients of the explanatory variables, which in turn can be calculated easily from the correlation matrix of the explanatory variables.
The estimate proposed in this work can be useful in several applications. As we already noted, meta-analysis of regression coefficients is increasingly being used in several applications both in the biological [6] [7] [45] as well as in the social sciences [8] -[11] . Thus, the estimate proposed here, coupled with the advances in multivariate meta-analysis software, can facilitate further the use of the method. Some other, more advanced techniques have also been proposed for synthesizing regression coefficients, especially when the studies are included in the meta-analysis evaluate different set of explanatory variables [46] [47] . However, these techniques require specialised software or user-written code, whereas the traditional approach mentioned here can be fitted using standard software for multivariate meta-analysis. Finally, the influence of the omitted variables (i.e. the variables that are not measured in some of the included studies), can be evaluated and adjusted for using multivariate meta-regression, simply by adding an indicator variable for each of the omitted covariates. We believe that such an approach will be efficient and easily used.
The method proposed here, can also greatly increase the usability of the standard synthesis analysis method. For instance, such methods can be used for constructing multivariate prognostic models using the univariate associations. Of particular importance is the ability to incorporate published univariable associations in diagnostic and prognostic models [14] , or the ability to adjust the results of an individual data analysis, for another recently discovered factor, using estimates from the literature [14] [48] .
Other potential applications can be found in the social sciences, where statistical methods for comparing regression coefficients between models [49] are needed, especially in the study of mediation models, such as in the case of psychology [50] . Moreover, as we showed in the manuscript, the method is already available for use also with the standardized regression coefficients (b). Even though the use of standardized regression coefficients in epidemiology has been the subject of debate [9] [51] [52] , they are routinely used in the social sciences [53] and they become popular in genetics with genome-wide association studies [54] -[56] . Thus, we believe that the method can be useful also in this respect.
The assumptions, on which the method is based, need also to be discussed. For the derivation we assume that the dependent and the independent variables are jointly multivariate normally distributed. This is one of the two main approaches for formulating a regression problem (the other is the approach that assumes that the independent variables are fixed by design). Even though the two approaches are conceptually very different, it is well known that concerning the estimation of the regression parameters (the coefficients and their variance), they yield exactly the same results. The assumption of multivariate normality is more stringent, but it yields an optimal predictor among all choices, rather than merely among linear predictors. Practically, since the estimators are identical, this means that we can use the expressions derived here, even in the case of binary independent variables and in any case the results are identical with the ones produced by any standard linear regression software. We need to mention at this point that the method is developed in [13] , which as the authors claimed does not make the assumption of normality, yields estimates for the regression coefficients that differ from the ones produced by standard regression packages.
When it comes to binary dependent variables however, the situation is more complicated. The method can also be used, after appropriate transformations, for estimating the parameters of such models (i.e. logistic regression). Several similar methods have been proposed in the literature [57] [58] , but they are all based on the method of Cornfield [59] , which is approximate and produces biased estimates [60] -[62] . This fact, along with some other fundamental differences between the linear model and the logistic regression model [63] [64] , rings the bell for the use of such methods, and makes imperative the need for new accurate methods for binary data.
Acknowledgements
This work is part of the project “IntDaMuS: Integration of Data from Multiple Sources” which is implemented under the “ARISTEIA ΙΙ”. Action of the “OPERATIONAL PROGRAMME EDUCATION AND LIFELONG LEARNING” and is co-funded by the European Social Fund (ESF) and National Resources.
Appendix A
Consider the ![]() diagonal matrix
diagonal matrix ![]() such that
such that![]() . From Equation (4) and Equation (16), it is obvious that
. From Equation (4) and Equation (16), it is obvious that
![]() , (A.1)
, (A.1)
which implies:
![]() (A.2)
(A.2)
Reminding that for each ![]() holds
holds
![]() (A.3)
(A.3)
Using Equations (5), (A.3), (A.2), (16) and the Hadamard product![]() , we can write:
, we can write:
![]() (A.4)
(A.4)
Denoting
![]() (A.5)
(A.5)
Equation (A.4) yields:
![]() (A.6)
(A.6)
Finally, denoting
![]()
and combining Equations (A.6) and (A.5) we derive:
![]()
Appendix B
Consider the ![]() matrix of the standardized regression coefficients b, the well known correlation matrices
matrix of the standardized regression coefficients b, the well known correlation matrices ![]() and
and ![]()
![]() ,
, ![]() ,
, ![]()
and, the ![]() diagonal matrix
diagonal matrix ![]() such that. As in Appendix A, Equation (A.1) yields:
such that. As in Appendix A, Equation (A.1) yields:
![]() (B.1)
(B.1)
Using Equation (B.1), Equation (16) and Equation (17), we derive:
![]() (B.2)
(B.2)
Equation (B.2) follows:
![]()
Appendix C
Let ![]() be an
be an ![]() matrix,
matrix, ![]() be the
be the ![]() matrix of 1 s, with
matrix of 1 s, with
![]()
It is well known that
![]() , (C.1)
, (C.1)
where the ![]() diagonal matrix
diagonal matrix ![]() is define
is define
![]() and
and ![]() denotes the correlation matrix.
denotes the correlation matrix.
It is obvious that
![]()
and using the definition of the Pearson’s correlation coefficient
![]() (C.2)
(C.2)
for![]() , the matrix
, the matrix ![]() is written as:
is written as:
![]() (C.3)
(C.3)
Notice that from (C.1) arises
![]() (C.4)
(C.4)
Furthermore, for the matrix ![]()
![]() , (C.5)
, (C.5)
where ![]() denotes the
denotes the ![]() adjoint matrix of
adjoint matrix of![]() , (see Applied Linear regression, Sanford Weisberg (2007), p. 57). Adjoint is defined the matrix, whose
, (see Applied Linear regression, Sanford Weisberg (2007), p. 57). Adjoint is defined the matrix, whose ![]() th element is formulated as:
th element is formulated as:
![]() (C.6)
(C.6)
where ![]() denotes the determinant of the
denotes the determinant of the ![]() submatrix of
submatrix of ![]() obtained by deleting the i-th row and j-th column of
obtained by deleting the i-th row and j-th column of![]() . Remind that
. Remind that ![]() is a symmetric matrix, since
is a symmetric matrix, since![]() . Combining the above remark, Equation (C.6), the properties of determinant and
. Combining the above remark, Equation (C.6), the properties of determinant and ![]() by Equation (C.3), the
by Equation (C.3), the ![]() th element of
th element of ![]() can be written as:
can be written as:
![]()
![]()
Thus, we conclude
![]() (C.7)
(C.7)
where
![]() (C.8)
(C.8)
In Equation (C.5) the ![]() th element of
th element of ![]() is denoted
is denoted ![]() and obtained by Equation (C.4), Equation (C.7) and Equation (C.8). In particular,
and obtained by Equation (C.4), Equation (C.7) and Equation (C.8). In particular,
![]()
and using the definition of correlation ![]() by Equation (C.2) the above equation is written
by Equation (C.2) the above equation is written
![]() (C.9)
(C.9)
![]() (C.10)
(C.10)
The i-multiple correlation coefficient is denoted by ![]() or
or ![]() and given [28]
and given [28]
![]()
whereby arises
![]() (C.11)
(C.11)
Remind that in Equation (C.11) the correlation matrix ![]() is a symmetric positive definite matrix, hence
is a symmetric positive definite matrix, hence ![]() and
and![]() , for every
, for every![]() , as a main submatrix of
, as a main submatrix of![]() . Since Equation (C.11) yields
. Since Equation (C.11) yields
![]()
by the above equality for ![]() we can write:
we can write:
![]() (C.12)
(C.12)
For ![]() the ij-partial correlation coefficient is denoted by
the ij-partial correlation coefficient is denoted by![]() , and defined [28]
, and defined [28]
![]()
whereby for every![]() , it is implied
, it is implied
![]() (C.13)
(C.13)
Substituting Equation (C.12) and Equation (C.13) in Equation (C.10) arises:
![]()
Moreover, for ![]() combining Equations (C.9) and (C.11) the variance of
combining Equations (C.9) and (C.11) the variance of ![]() is derived as follows:
is derived as follows:
![]()
Appendix D
** Dataset concerning Diabetes in Pima Indians
** Several constraints were placed on the selection of these instances from a larger database.
** In particular, all patients here are females at least 21 years old of Pima Indian heritage.
** http://archive.ics.uci.edu/ml/datasets/Pima+Indians+Diabetes
** Bache, K. & Lichman, M. (2013). UCI Machine Learning Repository
** [http://archive.ics.uci.edu/ml]. Irvine, CA: University of California,
** School of Information and Computer Science.
** Smith, J.W., Everhart, J.E., Dickson, W.C., Knowler, W.C., & Johannes, R.S. (1988).
** “Using the ADAP learning algorithm to forecast the onset of diabetes mellitus”.
** In Proceedings of the Symposium on Computer Applications and Medical Care} (pp. 261--265).
** IEEE Computer Society Press.
** Plasma glucose concentration at 2 hours in an oral glucose tolerance test
** (this is the dependent variable here)
sum glucose
scalar n=r(N)
scalar y= r(mean)
scalar S11=r(Var)
** the independent variables
** Diastolic blood pressure (mm Hg)
** Triceps skin fold thickness (mm)
** 2-Hour serum insulin (mu U/ml)
** Body mass index (weight in kg/(height in m)^2)
** Age (years)
** obrain the correlation matrix of the predictors
corr dbp thickness insulin bmi age
mat R22=r(C)
mat R22inv=invsym(R22)
** obtain the covariance matrix
corr dbp thickness insulin bmi age,cov
mat S22=r(C)
** obtain the full covariance matrix
corr glucose dbp thickness insulin bmi age,cov
mat S=r(C)
scalar col=colsof(S)
mat S12=S[1, 2..col]
mat S21=S[2..col, 1]
mat S22=S[2..col, 2..col]
**obtain the full correlation matrix
corr glucose dbp thickness insulin bmi age
mat R=r(C)
mat Ryx=R[2..6, 1]
mat Rk=R[2..6, 2..6]
mat bs=invsym(Rk)*Ryx
** implementation of the Samsa, Hu and Root method
matrix A = J(1,5,0)
scalar k=1
foreach x in dbp thickness insulin bmi age {
qui reg glucose `x’
mat bb=e(b)
mat A[1, k]=bb[1,1]
scalar k=k+1
}
local col2=col-1
matrix temp=vecdiag(S22)
matrix SS = J(1,5,0)
forvalues i=1(1) `col2’ {
mat SS[1,`i’]=sqrt(temp[1,`i’] )
}
mat AS=hadamard(A,SS)
mat AAS= R22inv*AS’
matrix bs2 = J(5,1,0)
forvalues i=1(1) `col2’ {
mat bs2[`i’,1]=AAS[`i’,1]/SS[1,`i’]
}
mat list bs2
** the standard method from multivariate analysis (the results are identical)
mat b=invsym(S22)*S21
mat list b
*calculation of sigma-squared
mat sigma2=S11-S12*b
** because this is estimated, we need to take it into account
scalar sigma2=(sigma2[1,1]*(n-1))/(n-6)
** calculation of R-squared for the independent variables
mat Sx=vecdiag(S22)
matrix R2 = J(1,5,0)
forvalues i=1(1) `col2’ {
mat R2[1,`i’]=1-1/R22inv[`i’ , `i’ ]
}
scalar detR=det(R22)
** calculation of the Rkij matrix which contains the determinants of the R22 matrix removing each ** time a row and a column
matrix Rkij = J(5,5,0)
preserve
clear
forvalues i=1(1) `col2’ {
forvalues j=1(1) `col2’ {
qui svmat R22
qui drop R22`i’
qui drop in `j’
qui mkmat R22*,mat(Rii`i’`j’)
mat Rkij[`i’, `j’]=det(Rii`i’`j’)
clear
}
}
restore
** calculation of the Partial Correlation coefficients (stored in matrix Rp)
matrix Rp = J(5,5,0)
forvalues i=1(1) `col2’ {
forvalues j=1(1) `col2’ {
scalar ex=`i’+`j’+1
mat Rp[`i’, `j’]=(-1)^(ex)*(Rkij[`i’, `j’]/(sqrt(Rkij[`i’, `i’])*sqrt(Rkij[`j’, `j’])))
}
}
** calculation of the covariance matrix of the regression coefficients
** (stored finally in matrix Vb)
matrix seb = J(1,5,0)
forvalues i=1(1) `col2’ {
mat seb[1,`i’]=sqrt(sigma2/((n-1)*S22[`i’, `i’]*(1-R2[1, `i’])))
}
mat vb=diag(seb)
mat Vb=-vb*Rp*vb
mat list Vb
reg glucose dbp thickness insulin bmi age
mat list e(V)
NOTES
![]()
*Corresponding author.