Generating Totally Positive Toeplitz Matrix from an Upper Bidiagonal Matrix ()
Received 17 September 2015; accepted 29 November 2015; published 2 December 2015


1. Introduction
Total positive matrices arise in many areas in mathematics, and there has been considerable interest lately in the study of these matrices. For background information see the most important survey in this field by T. Ando [1] . See also [2] .
A matrix A is said to be totally positive, if every square submatrix has positive minors and A is said to be totally nonnegative, and if every square submatrix has nonnegative minors. While it is well known that many of the nontrivial examples of totally positive matrices are obtained by restricting certain kernels to appropriate finite subsets of R (see, for example, Ando ( [1] , p. 212) or Pinkus ( [3] , p. 2). For Toeplitz matrices, that is, ma-
trices of the form 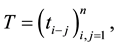 a complete characterization of the total positivity, in terms of certain entire
a complete characterization of the total positivity, in terms of certain entire
functions, has been studied in a series of references by Ando [1] , Pinkus [3] and S.M. Fallat, C.R. Johnson [4] .
Expressing a matrix as a product of lower triangle matrix L and an upper triangle matrix U is called a LU factorization. Such factorization is typically obtained by reducing a matrix to an upper triangular matrix from via row operation, that is, Gaussian elimination.
The primary purpose of this paper is to provide a new totally positive matrix generated from a totally nonnegative one and to construct its factorization.
The organization of our paper is as follows. In Section 2, we introduce our notation and give some auxiliary results which we use in the subsequent sections. In Section 3, we recall from [3] the Toeplitz matrices speci-
fied for the case , on which our proofs heavily rely. In Section 4, we present the proofs of our main
, on which our proofs heavily rely. In Section 4, we present the proofs of our main
results. In last section, we present the factorization of this resulted matrix.
2. Notation and Auxiliary Results
2.1. Notations
In this subsection we introduce the notation that will be used in developing the paper. For 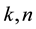 we denote by
we denote by 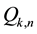 the set of all strictly increasing sequences of k integers chosen from
the set of all strictly increasing sequences of k integers chosen from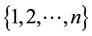 . For
. For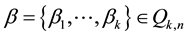
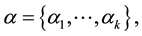 , we denote by
, we denote by 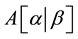 the
the  submatrix of A contained in the rows indexed by
submatrix of A contained in the rows indexed by 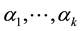 and columns indexed by
and columns indexed by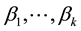 . A matrix A is called totally positive (abbreviated TP henceforth) and totally nonnegative (abbreviated TN) if
. A matrix A is called totally positive (abbreviated TP henceforth) and totally nonnegative (abbreviated TN) if 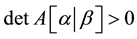 and
and 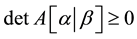 , respectively, for all
, respectively, for all
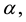 . If a totally nonnegative matrix is also nonsingular, we write NsTN.
. If a totally nonnegative matrix is also nonsingular, we write NsTN.
Definition 2.1.1 [3]
A square lower (upper) triangular matrix A is called lower (upper) triangular positive matrix, denoted LTP (UTP), if for all ![]() and for
and for ![]() with the property that
with the property that ![]() (
(![]() ) for
) for![]() , then
, then![]() .
.
Let I be the square identity matrix of order n, and for![]() , we let
, we let ![]() be the square standard basis matrix whose only nonzero entry is 1 that occurs in the
be the square standard basis matrix whose only nonzero entry is 1 that occurs in the ![]() position.
position.
A tridiagonal matrix that is also upper (lower) triangular is called an upper (lower) bidiagonal matrix. Statements referring to just triangular or bidiagonal matrices without the adjectives “upper” or “lower” may be applied to either case.
2.2. Auxiliary Results
We use the following classic formula known as Cauchy-Binet formula and stated in the theorem below.
Theorem 2.2.1 (Cauchy-Binet formula) ( [4] , p. 27). Let A be an ![]() matrix and B be an
matrix and B be an ![]() matrix then for each pair of indexed sets
matrix then for each pair of indexed sets ![]() and
and ![]() of cardinality k, where
of cardinality k, where![]() , we have
, we have
![]()
The following remarkable result is one of the most important and useful results in the study of TN matrices. This result first appeared in [5] see also [1] for another proof of this fact.
Theorem 2.2.2. Let ![]() be a square matrix of order n. Then A is NsTN if and only if A has an LU
be a square matrix of order n. Then A is NsTN if and only if A has an LU
factorization, such that both L and U are NsTN square matrices.
Using this theorem and Cauchy-Binet formula we have the following corollary.
Corollary 2.2.3 [6] . Let ![]() be a square matrix of order n. Then A is TP if and only if A has an LU
be a square matrix of order n. Then A is TP if and only if A has an LU
factorization, such that both L and U are TP square matrices.
We have the following theorem to prove both L and U are totally positive.
Theorem 2.2.4. Let ![]() be an upper triangular square matrix of order n satisfying
be an upper triangular square matrix of order n satisfying
![]() for,
for,
Then U is UTP (upper totally positive). Similarly, if ![]() is an lower triangular square matrix of order
is an lower triangular square matrix of order
n satisfying ![]() for
for![]() ,
,![]() . Then L is LTP (lower totally positive).
. Then L is LTP (lower totally positive).
In the sequel we will make use the the following lemma, see, e.g. [7] .
Lemma 2.2.5 (Sylvester Identity)
Partition square matrix T of order n, ![]() , as:
, as:
![]() ,
,
where ![]() square matrix of order
square matrix of order ![]() and
and ![]() and
and ![]() are scalars. Define the submatrices
are scalars. Define the submatrices
![]()
Then if ![]() is non singular
is non singular
![]()
3. Toeplitz Matrices
Assuming we are given a finite sequence ![]() of distinct real numbers, the associated To-
of distinct real numbers, the associated To-
eplitz matrix is defined by ![]() or
or![]() . If we are given a one-sided finite sequence
. If we are given a one-sided finite sequence![]() ,
,
then we understand this to mean that ![]() in the above definition. Sequences that give rise to totally positive Toeplitz matrices have been totally characterized in terms of their generating functions, i.e. re-
in the above definition. Sequences that give rise to totally positive Toeplitz matrices have been totally characterized in terms of their generating functions, i.e. re-
presentations of![]() .
.
In our case, the normalization![]() , the sequence
, the sequence ![]() gives rise to a totally positive Toeplitz matrix
gives rise to a totally positive Toeplitz matrix
![]() if and only if
if and only if ![]() has the form
has the form
![]()
where![]() .
.
Now consider the polynomial![]() , the upper triangular Toeplitz matrix
, the upper triangular Toeplitz matrix
![]()
is TP.
4. Generating New Form of Toeplitz Matrix
4.1. Main Result
Now we formalize the structure of our result by the following theorem.
Theorem 4.1.1. Assume that we are given the sequence ![]() of
of ![]() distinct positive real numbers.
distinct positive real numbers.
Define the upper bidiagonal matrix ![]() by
by
![]()
That is the sequence ![]() lies on the superdiagonal. Then the matrix T defined as
lies on the superdiagonal. Then the matrix T defined as
![]()
is TP.
Proof
To prove this result we must note that
![]()
where ![]() is upper triangular matrix and
is upper triangular matrix and ![]() is lower triangular matrix. By corollary 2.2.3 A is TP if both U and L are TP.
is lower triangular matrix. By corollary 2.2.3 A is TP if both U and L are TP.
So, want to prove ![]() is upper TP.
is upper TP.
![]()
By Theorem 2.2.4 U is TP if
![]()
where ![]() which is positive and
which is positive and
![]()
Since its submatrix of Toeplitz matrix.
Illustrative Example
Let we have the following sequence of distinct positive real numbers 1, 4, 3.
Define the matrix A as:
![]()
Then the matrix function
![]()
is TP.
4.2. Properties
1) Note that ![]() since
since ![]() and
and
![]()
Using this property we prove the following lemma
Lemma 4.2.1. The matrix T, as defined above has the following property
![]()
where ![]() and
and ![]() are defined in Lemma 2.2.5.
are defined in Lemma 2.2.5.
Proof
The statement follows by Lemma 2.2.5 and the idea of![]() .
.
2) Let P denote the square matrix of order n permutation matrix by the permutation
![]() ,
, ![]() , and suppose T is a square TP Toeplitz matrix. Then
, and suppose T is a square TP Toeplitz matrix. Then ![]() is TP too (see
is TP too (see
[7] ). Moreover, ![]() is TP, where S is diagonal matrix with diagonal entries alternately 1 and -1.
is TP, where S is diagonal matrix with diagonal entries alternately 1 and -1.
3) The Hadamrd product of two TP toeplitz matrices is TP matrix too, that is if we are given two square TP
matrices ![]() and
and ![]() of order n. Then the Hadamard product
of order n. Then the Hadamard product ![]() is TP.
is TP.
5. Factorization
5.1. Construct New Factorization
Our aim is to write the new TP Toeplitz matrix T as a product of elementary matrices of a special form. For any![]() , we let
, we let ![]() to be the elementary lower matrix whose entries are defined by
to be the elementary lower matrix whose entries are defined by
![]()
Note that ![]() can be written as
can be written as![]() , where I is square identity matrix of order n and
, where I is square identity matrix of order n and ![]() is square matrix of order n whose non-zero entry is a 1 in the
is square matrix of order n whose non-zero entry is a 1 in the ![]() position n. Also, notice that
position n. Also, notice that![]() .
.
We use the elementary matrices ![]() to reduce Lower diagonal matrix to identity matrix.
to reduce Lower diagonal matrix to identity matrix.
For example, we can consider the following ![]() Lower diagonal matrix L
Lower diagonal matrix L
![]()
It can be factorized as
![]()
5.2. General Characterization
We begin a definition and a result that characterize the TP Toeplitz matrix T in terms of the elementary matrices![]() .
.
Theorem 5.2.1. Any square Toeplitz matrix of oreder n, ![]() can be written as
can be written as
![]()
That is, ![]()
Illustrative Example
Let
![]()
The matrix in this example can be factorized as
![]()
Note that the number of the factored matrices equal
![]()