Estimation and Forecasting Survival of Diabetic CABG Patients (Kalman Filter Smoothing Approach) ()
1. Introduction
The Coronary Artery Disease (CAD) is a chronic disease, which progresses with age at different rates. CAD is a result of built-up of fats on the inner walls of the coronary arteries. Thus, the sizes of coronary arteries become narrow and as a result the blood flow to the heart muscles is reduced/blocked. Therefore, the heart muscles do not receive required oxygenated blood, which leads to the heart attack. CAD is a leading cause of death worldwide (see Hansson [3] , John [4] , and Sun and Hong [5] , William, Stephen, Thomas and Robert [6] ). The medical scientists Goldstein [7] and Jennifer [8] , William [6] are of the opinion that CABG is an effective treatment option for CAD patients. The medical research organizations like Heart and Stroke Foundation Canada [9] , American Heart Association [10] and Virtual Health Care Team Columbia have classified risk factors of CABG patients as modifiable (Hypertension, Diabetes, Smoking, High Cholesterol, Sedentary Lifestyle and Obesity) and non-modifi- able (Age, Gender and Family History-Genetic Predisposition).
William, Ellis, Josef, Ralph and Robert [6] carried out the survival study on incomplete population (progressive censoring of type 1) of CABG patients comprising 2011 patients using Kaplan Meier method [11] . The patients were grouped with respect to Male, Female, Age, Hypertension, Diabetes, and Ejection Fraction, Vessels, Congestive Heart Failure, Elective and Emergency Surgery. The patients were undergone through a first re-operation at Emory University hospitals from 1975 to 1993 (see William [12] . The patients were observed/followed up for 12 years. In the article [13] [14] we proposed a procedure, to make an IP, and a CP.
The Weibull distribution model has been used for survival analysis by Abrenthy [15] , Bunday [16] , Cohen [17] , Crow [18] , Gross and Clark [19] , Klein & Moeschberger [20] , Lang [21] , Lawless [22] , and Paul [23] . In particular, the survival study of chronic diseases, such as AIDS and Cancer, has been carried out using Weibull distributions by Bain and Englehardt [24] , Khan & Mahmud [23] [25] , Klein & Moeschberger [20] , Lawless [22] and Swaminathan and Brenner [26] . Lanju & William [27] used Weibull distribution to human survival data of patients with plasma cell and in response-adaptive randomization for survival trials respectively. We [14] have carried out survival analysis of CABG patients by parametric estimations-classical approach, in modifiable risk factors (Hypertension and Diabetes).
The dynamic linear model (DLM) and Kalman Filter (KF) equations have been described by Harrison and Steven [28] . According to the researchers, Sorenson [2] and Greg [29] Kalman Filter is a mathematical technique, used to estimate the state of a process by minimizing error of estimation. Kalman Filter extracts signals from a series of incomplete and noisy measurements. It removes noises from the process parameters and retains useful information. Kalman filter estimates the state of a dynamic linear model through its recurrence equations which minimizes the variance of estimation error. To implement Kalman filter, observed values as dependent variables are required for updating the process parameters. Though, since time of introduction, the Kalman Filter has been subject of research for engineering processes see Frank [30] , however the KF methodology has been applied extensively in medical research/life-testing studies/survival analysis; for example, Meinhold and Singpurwalla [31] proposed a new method for inference and extrapolations in certain dose-response, damage-assess- ment, and accelerated-life-testing studies, using Kalman-filter smoothing. Anatoli, Kenneth and James [32] indicated that various multivariate stochastic process models have been developed to represent human physiological aging and mortality. These researchers considered the effects of observed and unobserved state variables on the age trajectory of physiological parameters. The parameters of the distribution used were estimated based on an extension of the theory of Kalman filters to include systematic mortality selection. Ludwig [33] considered models for discrete time panel and survival data; and used a generalized linear Kalman filter approach.
In our study, Kalman filter technique is applied to estimate parameters of Weibull probability distribution using Diabetic and Non Diabetic CABG patient’s data sets. For construction of KF equations, survivor function of the probability distribution is linearized by transformation of double-log. The procedure to construct linear form of the survivor function, as advocated by researchers (see Gross and Clark [19] , Kalbfleisch and Prentice [34] and Lawless [22] , Meinhold and Singpurwalla [35] ) is followed. Survival proportions for complete population of Diabetic CABG patients obtained from Kaplan Meier method are used as observed values 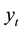 at time t, for updating the time varying parameters of the distribution. After defining the updating system of parameters of a probability distribution with KF approach (discussed in the methodology), the parameters are estimated at each time t by maximizing likelihood function of double-lognormal distribution, through Davidon-Fletcher-Powel method of optimization [36] . Since, in KF approach the observed values are from complete population, therefore, censored part is excluded (dropped) from log-likelihood function. The survival proportions obtained by the pro- bability distributions with KF approach are presented with respect to Diabetic and Non Diabetic patients i.e. Diabetes Present (
at time t, for updating the time varying parameters of the distribution. After defining the updating system of parameters of a probability distribution with KF approach (discussed in the methodology), the parameters are estimated at each time t by maximizing likelihood function of double-lognormal distribution, through Davidon-Fletcher-Powel method of optimization [36] . Since, in KF approach the observed values are from complete population, therefore, censored part is excluded (dropped) from log-likelihood function. The survival proportions obtained by the pro- bability distributions with KF approach are presented with respect to Diabetic and Non Diabetic patients i.e. Diabetes Present ( ) and Diabetes Absent (
) and Diabetes Absent (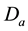 ) Groups of CABG patients.
) Groups of CABG patients.
2. Methodology
For the estimation of survival proportions Kaplan Meier [11] proposed a method and latter discussed by William
[6] and Lawless [22] i.e. , where
, where 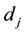 and
and  are the number of items failed (died indi-
are the number of items failed (died indi-
viduals/patients) and number of individuals at risk at time 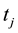 respectively, that is, the number of individuals survived and uncensored at time
respectively, that is, the number of individuals survived and uncensored at time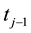 .This method may be applied to both censored and uncensored data, see Lawless [22] . In case of censored individuals (items) the analysis is performed on IP. Khan, Saleem & Mahmud [1] proposed that the censored individuals
.This method may be applied to both censored and uncensored data, see Lawless [22] . In case of censored individuals (items) the analysis is performed on IP. Khan, Saleem & Mahmud [1] proposed that the censored individuals 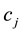 may be taken into account. The inclusion of splitted-censored in-
may be taken into account. The inclusion of splitted-censored in-
dividuals, 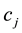 proportionally
proportionally 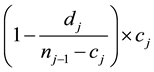 and
and 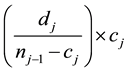 into known survived,
into known survived, 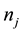 and died in-
and died in-
dividual’s 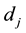 respectively make populations complete. Thus the survival analysis may be performed on the CP from its IP. We apply Kaplan Meier method on CP of
respectively make populations complete. Thus the survival analysis may be performed on the CP from its IP. We apply Kaplan Meier method on CP of ![]() and
and ![]() groups of CABG patients to obtain survival proportions
groups of CABG patients to obtain survival proportions![]() ’s and use as input in the DLM and KF equations/process. In this study the observed values (survival proportions) are denoted by
’s and use as input in the DLM and KF equations/process. In this study the observed values (survival proportions) are denoted by![]() , where
, where ![]() may take value
may take value ![]() at time
at time ![]() . Harrison and Stevens [28] described the DLM which may be reproduced as system of following two equations:
. Harrison and Stevens [28] described the DLM which may be reproduced as system of following two equations:
Observation Equation:
![]() (1)
(1)
System Equation:
![]() (2)
(2)
where ![]() and
and ![]() are of arbitrary dimensions.
are of arbitrary dimensions. ![]() is a scalar,
is a scalar, ![]() is vector of process parameters at time t,
is vector of process parameters at time t, ![]() is matrix of independent variables, known at time t, G is known system matrix (identity matrix),
is matrix of independent variables, known at time t, G is known system matrix (identity matrix), ![]() is error term, a difference between observed and expected value
is error term, a difference between observed and expected value![]() and
and ![]() respectively at time t.
respectively at time t. ![]() is the variance of
is the variance of![]() . It is assumed that
. It is assumed that ![]() has Gaussian distribution with mean 0 and variance
has Gaussian distribution with mean 0 and variance![]() . The system equation describes the change which occurs when process parameter changes from preceding value
. The system equation describes the change which occurs when process parameter changes from preceding value ![]() to current value
to current value ![]() and
and ![]() is the variance of disturbance term
is the variance of disturbance term![]() . According to Harrison and Stevens (1976), it is assumed that distribution of the parameter vector
. According to Harrison and Stevens (1976), it is assumed that distribution of the parameter vector ![]() at time t = 0 i.e.
at time t = 0 i.e. ![]() prior to the first observation
prior to the first observation ![]() is in the form of normal probability distribution with mean say
is in the form of normal probability distribution with mean say ![]() and variance
and variance ![]() i.e.
i.e.![]() . If the observed values;
. If the observed values; ![]() are described through DLM, then the posterior distribution of parameter vector
are described through DLM, then the posterior distribution of parameter vector ![]() is also normally distributed with mean say
is also normally distributed with mean say ![]() and variance
and variance ![]() i.e.
i.e.![]() . Whereas, the values of
. Whereas, the values of ![]()
and ![]() are recursively obtained as:
are recursively obtained as:![]() ;
;![]() ;
;![]() ;
;![]() ;
;
![]() . The Kalman filter equations are:
. The Kalman filter equations are: ![]() and
and ![]() (for detail see Harrison and Stevens [28] ).
(for detail see Harrison and Stevens [28] ). ![]() is variance of
is variance of ![]() and
and ![]() is a matrix which update
is a matrix which update ![]() &
& ![]() at each time t recursively.
at each time t recursively.
The KF equations of Weibull probability distribution models are constructed by linearizing survival function of the distribution with transformation; double-log. The parameters of the probability distributions are estimated at each time t, by maximizing log-likelihood function of lognormal distribution (which is transformed form of Weibull distribution), through the Davidon-Fletcher-Powel method of optimization. For the entire system, the parametric space at each time point t is![]() . Specification of starting values of the parameters is a common difficulty in implementing Kalman Filter. Practitioners have to check the sensitivity of the final results with different sets of assumed values (see Meinhold and Singpurwalla, [31] . After obtaining the prior values of the parameters of the probability distributions at time t = 0, the values
. Specification of starting values of the parameters is a common difficulty in implementing Kalman Filter. Practitioners have to check the sensitivity of the final results with different sets of assumed values (see Meinhold and Singpurwalla, [31] . After obtaining the prior values of the parameters of the probability distributions at time t = 0, the values ![]() are obtained recursively by using the Kalman filter updating equations. The survival proportions for complete population of
are obtained recursively by using the Kalman filter updating equations. The survival proportions for complete population of ![]() and
and ![]() CABG patients are used as observed values
CABG patients are used as observed values![]() ’s at time t, for updating the time varying parameters of the distributions. Since, in the Kalman filter approach the observed values are from complete population, therefore, censored part is dropped from the log-likelihood function. To find maximum likelihood estimates we take negative log-likelihood function of the distribution. A subroutine for maximizing log-likelihood function of each distribution along with KF process is developed in FORTRAN program. The subroutine in-conjunction with the DFP optimization method is used to find the optimal initial estimates of the mean and variance parameters included in the model,
’s at time t, for updating the time varying parameters of the distributions. Since, in the Kalman filter approach the observed values are from complete population, therefore, censored part is dropped from the log-likelihood function. To find maximum likelihood estimates we take negative log-likelihood function of the distribution. A subroutine for maximizing log-likelihood function of each distribution along with KF process is developed in FORTRAN program. The subroutine in-conjunction with the DFP optimization method is used to find the optimal initial estimates of the mean and variance parameters included in the model, ![]() and
and![]() , from final iteration of the program. For outside sample period (forecasting), due to non-availability of dependent values
, from final iteration of the program. For outside sample period (forecasting), due to non-availability of dependent values![]() ) we stop the process of updating the mean parameters. Therefore, values of these optimal mean parameters remain constant and are utilized for updating the variance parameters for outside sample period, using the KF equations. The survival proportions
) we stop the process of updating the mean parameters. Therefore, values of these optimal mean parameters remain constant and are utilized for updating the variance parameters for outside sample period, using the KF equations. The survival proportions![]() ’s of these probability distributions are estimated.
’s of these probability distributions are estimated.
3. Application (Construction of KF Equations of Weibull Distribution)
Since the values of survival proportions ![]() (observed values) lies in the interval (0, 1), expected value,
(observed values) lies in the interval (0, 1), expected value, ![]() of a probability distribution should also lie in the interval (0, 1). Keeping in view the natural process of deaths with the passage of time, it is assumed that
of a probability distribution should also lie in the interval (0, 1). Keeping in view the natural process of deaths with the passage of time, it is assumed that ![]() as a function of t is monotonically decreasing. These re-
as a function of t is monotonically decreasing. These re-
searchers, Meinhold and Singpurwala [33] considered a quantity ![]()
![]() which is a
which is a
nonlinear, monotonically decreasing function of t and is survival function, ![]() of the Weibull distribution. Moreover, the form
of the Weibull distribution. Moreover, the form ![]() (where
(where ![]() and
and ![]() are scale and shape time varying parameters respectively in KF approach) has property with respect to linearity; may be linearized by taking its double logarithm. The linear
are scale and shape time varying parameters respectively in KF approach) has property with respect to linearity; may be linearized by taking its double logarithm. The linear
form is a requirement for filtering techniques. Thus to implement KF a random quantity ![]() is
is
defined, which require that ![]() has a Gaussian density with expectation
has a Gaussian density with expectation ![]() and variance
and variance![]() . This implies that the random quantity
. This implies that the random quantity ![]() must have double-lognormal distribution with pdfat
must have double-lognormal distribution with pdfat ![]() of the form:
of the form:
![]()
Now, ![]()
setting ![]()
![]() (3)
(3)
The corresponding system equation is:
![]() (4)
(4)
Comparing Equations (3) and (4) with (1) and (2), we find that:
![]() ,
,
![]() and
and ![]() (identity matrix).
(identity matrix).
To find maximum likelihood estimates we consider negative log-likelihood function say![]() ) of the double-lognormal distribution, given as:
) of the double-lognormal distribution, given as:
![]()
where, ![]() and
and ![]() are observed values from CP and
are observed values from CP and ![]() number of failures at time
number of failures at time ![]() respectively and
respectively and ![]() may
may
be obtained as:![]() .
.
For derivation of ![]() and its partial derivatives, see Appendix A.
and its partial derivatives, see Appendix A.
A subroutine for maximizing log-likelihood function of the double-lognormal distribution along with KF process (subroutine) is developed in FORTRAN program.
The subroutine in-conjunction with DFP optimization method is used to find the optimal initial estimates of the parameters included in the model ![]() and
and![]() , from final iteration of the program.
, from final iteration of the program.
The optimal initial estimates of parameters obtained by maximizing the log-likelihood function are presented in Table 1.
The results (survival proportions obtained by using Weibull distribution and KF approach ![]() at each
at each
time point t as explained earlier) of ![]() (Diabetic Absent) and
(Diabetic Absent) and ![]() (Diabetic Present) groups of CABG patients are presented in Table 2 and Table 3 respectively.
(Diabetic Present) groups of CABG patients are presented in Table 2 and Table 3 respectively.
![]()
Table 1. The estimates of parameters of Weibull distribution and KF using data of ![]() and
and ![]() groups of CABG patients.
groups of CABG patients.
![]()
Table 2. Survival proportions ![]() of 12 years estimated and 3 years forecasted of CP (complete population) of
of 12 years estimated and 3 years forecasted of CP (complete population) of ![]() (diabetic absent group) of CABG patients obtained by Kalman Filter approach.
(diabetic absent group) of CABG patients obtained by Kalman Filter approach.
4. Conclusion
The graphs of observed survival proportions from the complete population ![]() and expected survival proportions
and expected survival proportions ![]() of
of ![]() and
and ![]() groups of CABG patients (Figure 1 & Figure 2) indicate that the behavior of
groups of CABG patients (Figure 1 & Figure 2) indicate that the behavior of ![]() from
from ![]() group is like linear throughout the sample period, whereas
group is like linear throughout the sample period, whereas ![]() of the
of the ![]() group is almost linear for the first 7 values and curved for the rest of values; due to more noises, however it remains around
group is almost linear for the first 7 values and curved for the rest of values; due to more noises, however it remains around ![]() of the
of the![]() . This reflects that the complete population (forecasting) data has been modeled adequately. Kalman Filter smoothing approach is appropriate and forecast of
. This reflects that the complete population (forecasting) data has been modeled adequately. Kalman Filter smoothing approach is appropriate and forecast of ![]() and
and ![]() groups of CABG patients is reliable outside the sample observations.
groups of CABG patients is reliable outside the sample observations.
Acknowledgements
We are thankful to our reviewers, whose constructive criticism has resulted in a clearer presentation of our work and inclusion of additional useful reference material.
Appendix-A
The Double-Lognormal Distribution
Consider p.d.f of log-normal distribution:
![]() where
where ![]() and
and ![]() are parameters of the distribution.
are parameters of the distribution.
Let ![]() and
and ![]() or
or![]() ,
,
then,
![]() .
.
Let![]() , we may write as:
, we may write as: ![]()
To find maximum likelihood estimates, we consider negative log-likelihood function say![]() ) of the double- lognormal distribution, given as:
) of the double- lognormal distribution, given as:
![]() ,
,
where![]() , by excluding the censored part since observed values
, by excluding the censored part since observed values ![]() are from complete popula-
are from complete popula-
tion, ![]() are the number of failures (died) at time
are the number of failures (died) at time ![]() and
and ![]() may be obtained by replacing value of
may be obtained by replacing value of![]() . We get
. We get ![]() as:
as:
![]()
For partial derivatives, differentiating above equation with respect to ![]() and
and![]() , we get
, we get
![]()
and
![]()