Temporal Prediction of Aircraft Loss-of-Control: A Dynamic Optimization Approach ()
1. Introduction
Air crash analyses during the past decade have concluded that about 40 percent of fatal air accidents in civil aviation occur due to Aircraft Loss of Control (LOC), the most contributing factor amongst others [1] [2] . During this time span, LOC related research has received increased attention in the aviation safety community [3] . Several investigations were carried out to understand the nature and characteristics of loss-of-control regimes [3] -[5] . In particular, a collaborative effort between Boeing and NASA Langley [6] provided a flight envelope based method to quantify LOC from air accident data. Similar envelopes have been used in this work to quantify LOC boundaries.
Quantifying LOC boundaries is a first step toward addressing the larger issue of LOC prevention. While there exist envelope protection features on an aircraft, they are of little use during LOC flight regimes due to degradation of normal control modes [7] . An alternative approach is to provide useful LOC information to pilots using flight states and pilot input data. Though LOC envelopes provide limits of operation of aircraft states and other auxiliary variables, there are not readily usable by the pilots. This is because, envelope data are provided in the flight state space whereas pilot decisions are executed in the control space. Furthermore, the mapping between the control-space inputs to state-space responses becomes unpredictable close to LOC regimes. This results in difficulty for human interpretation unlike flight regimes close to the trim conditions. However, it is possible to warn the pilot about potential LOC scenarios using intelligent algorithms by extracting accurate spatio-temporal information from the available LOC envelopes for direct pilot use. In this connection, recent experiments carried out at NASA Ames Research Center demonstrate favorable disposition of pilots to use pilot-friendly LOC tools [8] . A data based predictive control (DBPC) algorithm [9] was used to compute spatial control bounds for pilot use. However, in that work the time associated with the spatial bounds was considered fixed. This work complements the DBPC based spatial bounds by providing temporal bound information in framework of optimal control theory using Pontryagin’s Maximum Principle.
This remainder of the paper is structured as follows. Section 2 provides an overview of the minimum time problem. Section 3 treats the optimal control problem using Pontryagin Maximum Principle and describes the resulting two point boundary value problem (TP-BVP). The solution to the TPBVP using differential evolution (DE) based methods is described in Section 4. Simulation results based on linear longitudinal model from [4] are provided in Section 5 followed by discussion and concluding remarks in Section 6.
2. Problem Formulation
We consider the problem of obtaining the minimum time to exit the flight envelope for a linearized longitudinal aircraft model. Let the operating envelope be defined in the  state space for control limits in
state space for control limits in 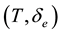 space as specified below [4] .
space as specified below [4] .
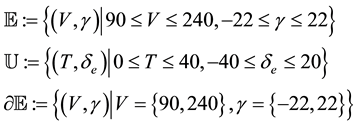
where,  denotes the flight envelope in (fps, deg) and
denotes the flight envelope in (fps, deg) and  denotes the envelope for the control bound in (lbf, deg). The boundary of the envelope is denoted by
denotes the envelope for the control bound in (lbf, deg). The boundary of the envelope is denoted by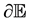 . The system is assumed to follow the dynamics [4] as shown below:
. The system is assumed to follow the dynamics [4] as shown below:
 (1)
(1)
where, 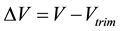 ,
, 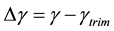 ,
, 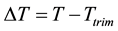 and
and . For convenience of notation, let
. For convenience of notation, let 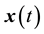 denote the state of the system trajectory at time t starting at
denote the state of the system trajectory at time t starting at 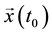 under the action of the control input
under the action of the control input 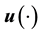 on
on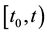 .
.
The optimal control problem is posed as follows: Given an initial point in state space ![]() at
at![]() , find the control input
, find the control input ![]() that minimizes the transfer time
that minimizes the transfer time ![]() to reach any point on
to reach any point on![]() . The control
. The control ![]() then becomes the optimal control input associated with minimum transfer time
then becomes the optimal control input associated with minimum transfer time![]() . We shall compute the optimal trajectory using the Pontryagin Maximum Principle (PMP). The readers are referred to [10] for a proof of existence of optimal controls in case of linear systems. In this work, the boundary
. We shall compute the optimal trajectory using the Pontryagin Maximum Principle (PMP). The readers are referred to [10] for a proof of existence of optimal controls in case of linear systems. In this work, the boundary ![]() is approximated with a finite number of points. Let
is approximated with a finite number of points. Let ![]() denote the
denote the ![]() point on the boundary by
point on the boundary by![]() . Thus the optimal control law
. Thus the optimal control law ![]() needs to be computed such that the point
needs to be computed such that the point ![]() is transferred to
is transferred to ![]() in minimum time
in minimum time![]() .
.
3. Minimum Time Problem
Consider the linear dynamical system given by:
![]() (2)
(2)
where, ![]() (state transition matrix) and
(state transition matrix) and ![]() (control matrix) are given by:
(control matrix) are given by:
![]()
The cost functional for the minimum time problem then becomes,
![]() (3)
(3)
where, ![]() is the free terminal time to be optimized. The Hamiltonian for this dynamic optimization problem is given by:
is the free terminal time to be optimized. The Hamiltonian for this dynamic optimization problem is given by:
![]() (4)
(4)
In the framework of PMP, the existence of an optimal control also mandates the existence of co-states (denoted by![]() ), whose dynamics are governed by:
), whose dynamics are governed by:
![]()
The optimal control law is the one that maximizes the Hamiltonian at every time step from ![]() to
to![]() . It is evident that such a control law would have a bang-bang structure since the Hamiltonian is affine in
. It is evident that such a control law would have a bang-bang structure since the Hamiltonian is affine in![]() . Thus,
. Thus,
![]()
and so, the control law can be expressed as:
![]() (5)
(5)
![]() (6)
(6)
where,![]() . This results in the TPBVP with the known initial and final states,
. This results in the TPBVP with the known initial and final states, ![]() and
and ![]() respectively as shown.
respectively as shown.
![]() (7)
(7)
subject to the boundary conditions:
![]()
![]()
![]() (8)
(8)
where, ![]() is necessary condition based on PMP to obtain the minimum final time
is necessary condition based on PMP to obtain the minimum final time![]() . The two point
. The two point
boundary value problem (TPBVP) is solved by matching the initial conditions of the unknown variables ![]() and
and ![]() so as to lead to the known final conditions described in Equation 8. This match between unknown guess and known final solutions provides the accurate map
so as to lead to the known final conditions described in Equation 8. This match between unknown guess and known final solutions provides the accurate map ![]() shown below:
shown below:
![]() (9)
(9)
In other words, the solution to the TPBVP is obtained by solving for the zeros of ![]() described in Equation 9. Due to the nonlinear nature of the composition maps to obtain
described in Equation 9. Due to the nonlinear nature of the composition maps to obtain![]() , analytical solutions are difficult to realize even for the case of linear systems (assuming they exist). Numerically, for the gradient based methods, step sizing for the update laws and good initial guesses are important factors for convergence. In such optimal control problems where the control law is bang-bang, small changes in the initial guess values could induce large changes in the gradients. For example, this scenario could arise when perturbations in
, analytical solutions are difficult to realize even for the case of linear systems (assuming they exist). Numerically, for the gradient based methods, step sizing for the update laws and good initial guesses are important factors for convergence. In such optimal control problems where the control law is bang-bang, small changes in the initial guess values could induce large changes in the gradients. For example, this scenario could arise when perturbations in ![]() or
or ![]() change the number of switches in the control law compared to the unperturbed case. In such cases, it could lead to jump discontinuities in the gradients and hence limit the gradient based solution techniques. In order to overcome this problem, we adopt a non-gradient marching technique based on stochastic swarm optimization using the differential evolution (DE) algorithm.
change the number of switches in the control law compared to the unperturbed case. In such cases, it could lead to jump discontinuities in the gradients and hence limit the gradient based solution techniques. In order to overcome this problem, we adopt a non-gradient marching technique based on stochastic swarm optimization using the differential evolution (DE) algorithm.
4. Differential Evolution for TPBVP
Differential Evolution (DE) is a metaheuristic iterative optimization strategy that tries to improve candidate solutions over generations. Since its inception in the mid 90s, there has been a growing interest in using DE due to its simple yet powerful approach to solve several engineering optimization problems [11] -[13] . In the framework of DE, each generation consists of population of candidate solutions, also known as agents. During every generation, each agent is moved a different position in the search space by a combination of update operations. If the new position of the agent is deemed better (based on a fitness measure), it is shortlisted to be a part of the next generation, else the original agent is retained. In this manner, the fitness of the solution candidates improves over generations. In this work, the DE algorithm was implemented as described below.
During the first generation, the population of guess vectors was initialized. Mutation was applied to each agent to generate the mutants. During the mutation step, a “local best” candidate was used along with the “global best” and “random” candidates to update the search direction, similar to that of Particle Swarm Optimization (PSO). These variants were crossed over with the existing agents based on a cross over probability (CR). In this implementation, a binomial crossover was performed to generate trial solutions which were compared to their counterparts from the original population to populate the next generation.
The objective function to be minimized is the final error, which depends on the initial conditions![]() ,
,![]() and hence approximating the roots of
and hence approximating the roots of![]() . Let the kth agent
. Let the kth agent ![]() during generation g be denoted by
during generation g be denoted by![]() . Also, let the kth agent’s best (minimum error) historical position as of current generation be represented by
. Also, let the kth agent’s best (minimum error) historical position as of current generation be represented by ![]() and let
and let ![]() denote the solution that results in least error
denote the solution that results in least error ![]() (as defined in Equation 9) compared to all other candidates in population across all generations. If F, CR, N, gmax denote the parameters corresponding to mutation weight, cross over probability, number of agents in population, maximum allowable generations respectively, then the flow chart depicting differential evolution solution is shown in Figure 1. In this work, the population was set to N = 100 candidates along with a crossover probability of CR = 0.4 and mutation weight F = 0.9.
(as defined in Equation 9) compared to all other candidates in population across all generations. If F, CR, N, gmax denote the parameters corresponding to mutation weight, cross over probability, number of agents in population, maximum allowable generations respectively, then the flow chart depicting differential evolution solution is shown in Figure 1. In this work, the population was set to N = 100 candidates along with a crossover probability of CR = 0.4 and mutation weight F = 0.9.
5. Results and Discussion
The solution to the TPBVP yields the initial conditions (IC) for forward simulation of the minimum time trajectories. The optimal control problems from an initial state ![]() to various points along the boundary
to various points along the boundary ![]() are solved and presented here. Figure 2 depicts optimal trajectories from
are solved and presented here. Figure 2 depicts optimal trajectories from ![]() to the corners of the rectangular envelope. The minimum time to envelope is approximated by computing minimum times to a collection of uniformly distributed points along the boundary as shown in Figure 4. The points along the boundary (“A” ... “L”) are color coded based on magnitude of transfer time from “O” to boundary point (BP) along the optimal path. Further, it can be inferred that the optimal trajectory computations for various initial conditions (ICs) could be simplified progressively by applying the principle of optimality. Thus, the optimal trajectory computation from an IC to BP (IC1-BP) overlapping with the optimal trajectory of another IC (IC2-BP) leverages information from the optimal trajectory computation of the latter.
to the corners of the rectangular envelope. The minimum time to envelope is approximated by computing minimum times to a collection of uniformly distributed points along the boundary as shown in Figure 4. The points along the boundary (“A” ... “L”) are color coded based on magnitude of transfer time from “O” to boundary point (BP) along the optimal path. Further, it can be inferred that the optimal trajectory computations for various initial conditions (ICs) could be simplified progressively by applying the principle of optimality. Thus, the optimal trajectory computation from an IC to BP (IC1-BP) overlapping with the optimal trajectory of another IC (IC2-BP) leverages information from the optimal trajectory computation of the latter.
It can also be observed from Figure 4 that some trajectories violate the bounds before the end point. In such cases, the minimum time to the boundary is estimated based on the first intersection with the boundary. Thus, the minimum time to envelope can be computed as the infimum of minimum times of all exit points under consideration. Table 1 depicts the minimum exit times for each trajectory. The infimum obtained corresponds to 0.1 sec along path OI (Figure 4). Though the low minimum time information is not readily useful, it can be argued that by restricting control bounds ![]() and applying the above approach, larger minimum times may be obtained.
and applying the above approach, larger minimum times may be obtained.
The convergence of the optimal solution using the Differential Evolution algorithm is shown in Figure 3, wherein the errors converge to zero in a finite number of generations. The corresponding optimal controls― namely thrust and elevator deflection and their bang-bang structure (due to affine nature of Hamiltonian w.r.t control inputs) are shown in Figure 5 and Figure 6 respectively.
6. Conclusion
This work investigated the issue of LOC prediction using tools from optimal control theory to develop spatio-
![]()
Table 1. Minimum time to end points in Figure 4.
![]()
Figure 1. Differential evolution for solving TPBVP.
![]()
Figure 2. Minimum time paths to corners.
![]()
Figure 4. Minimum time trajectories to corners.
temporal pilot aids. The time optimal problem to violate the Loss-of-control boundary was considered. The minimum time to reach any point on the boundary was computed using PMP. The resulting TPBVP was solved using Differential Evolution. Simulation of the linear longitudinal model was carried out in MATLAB and the optimal trajectories were found to be not necessarily the minimum phase space distance paths. The minimum time to envelope was computed as the infimum of minimum times to various boundary points. Future work could investigate minimum time trajectory generation over a space of initial conditions (IC), which would expedite optimal trajectory generation by leveraging the principle of optimality. Alternative strategies for solving TPBVP like hybrid optimization schemes could be explored to reduce computational loads and restricted control bounds could be considered to obtain practically viable minimum times. Further, the solution methodology employed here (using PMP-DE) can be readily extended to nonlinear models, which better characterize dynamics near LOC boundaries away from local trim conditions. In conclusion, this work provides an initial step to augment spatial pilot aids with minimum time temporal information aimed at LOC prevention.
Acknowledgements
The authors thank the NASA Ames research center for their support.