Gamma-Index Passing Rates in Baseline Plans Measured with a Detector Array ()
1. Introduction
A number of detector arrays have been developed for quality assurance (QA) of complex radiation treatment plans. Early-generation systems contained a set of detectors arranged in a line, e.g. Profiler 2, (Sun Nuclear Inc., Melbourne, FL) or in a plane, e.g. MatriXX (IBA Dosimetry GmbH, Schwarzenbruck, Germany). The latest instruments evolved to allow measuring the dose distribution in 3D space. Delta 4 (ScandiDos Inc., Uppsala, Sweden) consists of two planes of detectors arranged in “X” configuration and ArcCHECK (Sun Nuclear Inc., Melbourne, FL) consists of an array of detectors located on a cylindrical surface.
Several papers have been published to validate performance of each of these instruments. In particular, Feygelman et al. [1] developed a comprehensive set of tests for ArcCHECK and Delta 4, which included testing response of the individual detectors to variations in the fundamental beam properties, e.g. the absolute dose, as well as checking sensitivity to detecting errors for patient plans. Li et al. [2] examined sensitivity of ArcCHECK and Delta 4 to setup errors. Lin et al. added Monte Carlo computations into evaluation of ArcCHECK [3] , and examined the sensitivity to instrument misalignment for both ArcCHECK and MatriXX. Wang et al. [4] looked at detecting MLC positioning errors by inspecting ratios of the signal measured on the individual detectors of ArcCHECK. Stambaugh et al. [5] examined measured 3D dose distributions in selected clinical plans.
Historically, comparing multi-detector data to treatment planning system (TPS) data relied on calculations of the dose difference in flat portions of the dose distribution and of the distance to agreement (DTA) in regions of steep dose gradient. In 1998 Low et al. [6] introduced the gamma index, which combines the dose difference with the DTA, and provides an effective way of evaluating discrepancies between the measured dose distribu- tion and the one calculated with a TPS. Traditionally, the gamma index was evaluated with (3%, 3 mm) acceptance criteria [7] , which was recently shown not always to be sensitive enough to detect systematic errors, e.g. caused by incorrect setting of the dosimetric leaf gap (DLG) [8] , the excessively-averaged profiles used in the TPS, or the setup errors [9] . Nevertheless, the authors showed that in most cases sensitivity to detecting systematic errors could be increased to a satisfactory level by changing the acceptance criteria to (2%, 2 mm). Advantages of tightening-up the criteria used in the gamma index analysis were also confirmed by other authors, including Heilemann et al. [10] who used both Seven29 2D detector array (PTW, Freiburg, Germany) and Delta 4, and Li et al. [2] who used ArcCHECK and Delta 4. Several publications observed fairly weak correlation between the gamma index and the dose volume histogram (DVH) [11] - [13] , but due to its straightforward interpretation, gamma analysis remains a valuable QA method [14] .
Examples of the gamma passing rates in clinical scenarios have been published e.g. by Létourneau et al. 2009 [15] and Stambaugh et al. [5] , with the passing rates being reported for selected gamma acceptance criteria. García-Vicente et al. [16] studied the influence of the error in gantry rotation and leaf-positioning on the passing rates and on the DVH in selected sites (prostate and head & neck IMRT). Lin et al. [3] also analyzed the passing rates measured with ArcCHECK in multiple clinical plans, and the authors also compared the results to the corresponding Monte Carlo computations, providing an additional level of confidence. Vieillevigne et al. [17] analyzed gamma rates measured with several detector arrays in clinical plans, and examined sensitivity to detect errors.
The gamma analysis acceptance criteria are often established through analysis of the passing rates in a large number of clinical plans, but this is a labour-intensive approach. Moreover, it is implied that the linac is capable of delivering these plans at a satisfactory level no matter how complex the plans are. In spite of availability of many publications employing gamma analysis, there is no consensus on the choice of the % dose and mm crite- ria in the gamma index. We designed a protocol that addresses these problems, as well as we compared simple- case results to the theoretical prediction. We applied this protocol to measurements performed with ArcCHECK.
2. Methods and Materials
2.1. Plans
We designed separate plans for testing for dose errors and testing for spatial errors. In the absolute-dose mode we used a uniform-dose plan for the former. The uniform dose distribution was approximated by combining ex- posure from 5 rectangular fields (87 MU each, 400 MU/min) aiming at the ArcCHECK from different directions (gantry equal 216˚, 288˚, 0˚, 72˚ and 144˚). The center of ArcCHECK was set to the isocenter, and its axis was aligned with the longitudinal direction of the (non-rotated) couch. Each field delivered 87 MU, and was collimated to 24 cm along the axis of ArcCHECK to minimize exposure to the electronics, and 25 cm across. The calculated longitudinal dose profile passing through the central detector is shown in Figure 1(a)) (solid line). Errors in the dose were simulated by renormalizing the calculated plan. The % value of the renormalization was converted to the error in the dose by subtracting 100%. While it is more natural to introduce errors in the mea-
![]() (a) (b)
(a) (b)
Figure 1. Eclipse-calculated longitudinal dose profiles passing through the central detector in (a) the uniform dose plan (solid line) with no dose error, the quasi-uniform dose plan (dashed line) with error in dose (−4% shown here); and (b) in the plan with the dose gradient along the ArcCHECK axis. The shaded areas denote the ROIs used in the gamma analysis.
sured, not in the calculated dose, renormalizing the calculated plan provides equivalent passing rates under understanding that the sign of the error is opposite.
In the relative-dose mode we modified the plan described above by adding a small subfield (at gantry equal zero, and collimated to X = 1.2 cm and Y = 2 cm). The two central detectors irradiated under this subfield were used for normalization (to the maximum value), and the errors in the dose were simulated by changing the ratio of the weights between the subfield and the other fields. Subsequently, this plan will be referred to as the quasi-uniform plan, and the renormalization procedure as quasi-renormalization. The dose profile passing through the central detector for the quasi-uniform plan is plotted in Figure 1(a) (dashed line) when the dose is 96% for all detectors except the two detectors immediately next to the central axis (CAX).
We used an approximately constant dose gradient plan for testing in the presence of spatial errors. We accomplished this by replacing the open fields in the uniform plan with 60˚ (enhanced dynamic) wedges, for which the dynamic jaw was moving along the axis of ArcCHECK. The dose profile passing through the central detector is plotted in Figure 1(b). The geometrical errors were simulated by shifting the planed distributions within the software controlling ArcCHECK. 210 MU were delivered by each field (collimated to 20 cm along ArcCHECK axis and 25 cm across) at 400 MU/min.
All plans were calculated in Varian’s Eclipse (Varian Medical Systems, Palo Alto, CA) using anisotropic analytical algorithm (AAA) ver. 11.0.31, under 1 mm grid and with heterogeneity correction on. The plans were delivered with Varian TrueBeam 1.6 linac using 6 MV flat beams.
2.2. ArcCHECK Specific
We used ArcCHECK in all measurements of the dose distributions. The polymethyl methacrylate (PMMA) plug was inserted at all times. The instrument was levelled on the couch, and its center was aligned with the linac’s isocenter during all measurements. SNC Patient ver. 6.2.3 software (Sun Nuclear Corporation, Melbourne, FL, 2013) was used to control the instrument and to analyze the data. We used a virtual phantom in the shape of a cylinder matching the outline of ArcCHECK to calculate the dose distributions, and assigned uniform density with the CT# of 160 HU. Use of a uniform-density virtual phantom instead of an actual CT scan is recommended by the manufacturer. The CT# specified above was chosen to comply with a requirement of using the effective electron density of 1.150 g/cm3, and was adjusted by modifying the CT# of the virtual phantom until the ratio of the effective distance to the geometrical distance was 1.150. The plastic rails, which are a part of the mechanical support of the instrument, were included in the virtual phantom, as well as the couch (Varian Exact Couch Top with Flat Panel, using CT# = −300 HU for the surface and −1000 HU for the interior; no couch rails). We verified consistency of setting the CT# in the virtual phantom by measuring the ratio of the dose along the CAX in the upstream detector to the dose in the downstream detector. Strictly speaking, due to the lack of a detector along the CAX, an average of the doses in the two detectors nearest to the CAX was used. The measured ratio was 3.62, and was only 0.7% higher than the ratio calculated in the plan (the manufacturer allows up to 1% discrepancy).
We initially calibrated the dose in ArcCHECK by irradiating the instrument (positioned with its center at the linac’s isocenter) with 6 MV flat beam (10 cm × 10 cm, 200 MU), and assigning the dose of 262.1 cGy, which is the dose calculated at the depth of 3.3 cm in a virtual flat-water phantom on the CAX at the SSD = 86.3 cm. In order to refine the calibration, we recalibrated the instrument by assigning the dose of 263.6 cGy, which is the calculated dose at the depth of 2.8 cm in the virtual cylindrical phantom mimicking ArcCHECK placed at the isocenter. We subsequently performed a closed-loop type verification of this refined calibration by comparing the dose measured with ArcCHECK on the CAX at the depth of 2.8 cm to the calculated dose of 263.6 cGy. We averaged the measured dose based on the readings in six detectors placed within no more than 1 cm from the CAX on the upstream portion of the detector array. To eliminate the effect of the output instabilities of the linac on our results, we performed the dose calibration during each session.
The passing rates calculated by SNC Patient software employ an algorithm based on, but slightly different from the original algorithm introduce by Low et al. [6] : in the absolute dose mode, first the dose difference is verified, followed by the distance to agreement check, and the gamma index is calculated as described by Low et al. when the criteria mentioned above fail. For absolute-dose comparison under “global % difference” enabled and “measurement uncertainty” disabled it can be written as:
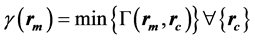 (1)
(1)
where
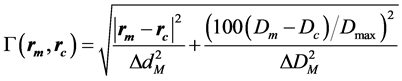 (2)
(2)
Dm and Dc are the measured and the calculated doses at the measured and the calculated position, rm and rc, respectively. Dmax is the maximum dose, ∆dM is the distance criterion and ∆DM is the dose difference criterion in %.
Due to the lack of spatial dependency in the uniform-dose plan, the theoretical passing rates (upon plan renormalization) were calculated through evaluating the dose difference only. In the theoretical prediction, 100% passing rate was assigned when the theoretical dose (same for every detector) did not differ from the planned value by more than the % dose criterion in the gamma index, and 0% otherwise. The detection rates for the true negative events (failure to detect the error in dose of the given % value) was calculated by subtracting the passing rate from 100%.
For the dose-gradient plan (using the “global % difference” = ON) we analyzed the passing rates upon shifting (in SNC Patient software) the planned dose distribution along the direction of the gradient. We used two methods to calculate the theoretical passing rates following the multi-step protocol employed by the SNC Patient software. We assigned 0% or 100% passing rates based on the dose-to-agreement check when using the % dose criterion of 0.01% (which approximates 0%, the value not allowed in the software). When the % dose was set to larger number, we proceeded as follows: we converted the dose profile into unitless space, where the shift divided by the distance criterion of the gamma index is used as the abscissa, and the dose * 100, divided by the maximum dose and the % dose criterion of the gamma index is used as the ordinate, see Figure 2. With the “global % difference” enabled (i.e. Van Dyk = ON), a uniform-gradient profile retains the linear shape in this unitless space, and the gamma index is simply the minimum distance between the planned line and the shifted line (i.e. with introduced error), and can be written as:
 (3)
(3)
where s is the mm shift along the gradient direction and α is the angular tilt of the profile line, see Figure 2. For a linear profile, the gamma index is independent on the value on the abscissa, and consequently the theoretical passing rates are same for every detector within the ROI.
![]()
Figure 2. The dose profile of the uniform-gradient plan in the unitless space remains linear when Van Dyk option is enabled. The gamma index in the presence of a shift error, when evaluated using Equation (3), is numerically equal to the minimum distance between the planned and the shifted dose profiles, and it is position independent.
The detection rates for the true negative events in the presence of a spatial error were calculated in a similar manner as for the dose error, i.e. 100%-passing rate, except now it is a function of the shift in mm instead of the error in the dose.
Unless specified otherwise, we used the following software options to compute the passing rates: absolute dose, Van Dyk (Global % Difference) = ON, Apply Measurement Uncertainty = OFF, Use 3D DTA for ArcCHECK = OFF, dose threshold (TH) = 10%.
We used a subset of all detectors in the analysis. For the uniform-dose and the quasi-uniform dose plans we excluded the first and the last loop of detectors from the region of interest (ROI). This is because we chose to limit the field size in order not to irradiate the electronics of the device, and consequently the dose was less uniform at these detector locations. The detectors utilized in the analysis are marked in the dose profile in Figure 1(a) as the shaded rectangle. We used the same ROI for the absolute dose and the relative dose testing. The error in the analysis of the relative-dose mode caused by not excluding the two central detectors from the analysis (the detectors used for normalization) is insignificant considering two detectors out of 1254 in the ROI constitute a small fraction.
We selected a smaller ROI, marked in Figure 1(b), for the gradient plans to constrain the analysis to the uniform-dose gradient region: only detectors located between z = −7 cm and −4 cm were used in the calculations. Strictly speaking, we adjusted the ROI from the rectangular shape to keep all detectors from the same loop of the spiral of the detectors within the ROI. The selected ROI is fairly close to the dose maximum, which is important in calculations with the option “Global % Difference” enabled, where the dose difference in the gamma index is referenced w.r.t. the maximum dose, not the dose at the detector location.
We repeated all measurements for the total of three or four times, each in a separate session, to estimate the uncertainties of the passing rates. As the setup was redone at the beginning of each session, the uncertainty of the setup is included in the error bars. The error bars plotted throughout this manuscript were calculated as the standard deviation of the mean.
3. Results
3.1. Error in Dose
The ratio of the measured to the calculated dose at the depth of 2.8 cm on the CAX in the closed-loop verification of the initial calibration was: 0.994 ± 0.003. The corresponding ratio for the refined calibration was 1.001 ± 0.003, which is better. We used the refined calibration in the subsequent measurements and analysis.
The passing rates as a function of the % dose criterion in the gamma index for ArcCHECK irradiated with the uniform-dose plan are shown in Figure 3 as black circles. The plan was calculated without introduction of any errors in the dose, i.e. no renormalization was applied. The project default options (summarized in section 2.2.) were used as the program options. The mm criterion is irrelevant in the uniform dose plan, and we arbitrarily chose 1 mm. The passing rate increases with an increase of the % dose criterion. In a perfect system, 100% of the detectors should pass at any non-zero % dose criterion, and smaller passing rates are a reflection of uncertainties in the system. The passing rate reaches 100% for % dose criterion of 1.5%, and such value may be used in routine analysis.
Also shown in Figure 3 are the passing rates with “measurement uncertainty” option enabled (red circles). This plot agrees very well with the behavior in a perfect system, but this is a consequence of a modified definition of the gamma index.
The γ(1.5%, 1 mm) in the uniform-dose plan as a function of the plan renormalization, i.e. the dose error (shown in the top axis), is plotted in Figure 4(a) (black open circles) for the default program options. The % dose criterion of 1.5% chosen in this plot corresponds to the previously established value allowing 100% passing rate in the absence of the dose error. The measurements roughly follow the hat-like shape of the theoretical prediction of an ideal system (black line). The maximum value reaches 100%, and the half width at the half maximum (HWHM) is 1.514% ± 0.002%, which is close to the theoretical value of 1.5%. A small centroid shift of 0.41% ± 0.06% of the theoretical data improves the agreement (blue line), but this value is small enough to consider not clinically significant. Unlike the theoretical prediction, the measured data does not have sharp transitions, which is due to intrinsic uncertainties. The measured 90 - 10 penumbra is 1.11% ± 0.06%. The value of the penumbra quantifies the transition region were false negatives and false positives occur, and is a measure of precision of the system to detect the error in the dose [18] .
The plot of the passing rates vs. the dose error is also useful in verifying the rate of detection of the true negative events for a given error. It should be noted that not all detectors of the array read the passing rates equal zero in the presence of the dose error equal the % dose criterion. In particular, the detection rate of the true negatives is only about 20% (100% - 80%) for −1.5% error, and 85% (100% - 15%) for 1.5% error. This is a consequence of system uncertainties. These rates are different for the positive and the negative error due to the presence of the (small) centroid shift. All true negatives are detected (i.e. 0% passing rate) only when the error is ±3% or larger. This value is significantly larger than the % dose criterion. Also plotted in Figure 4(a) are the passing rates for a larger value of the % dose criterion: γ(3%, 1 mm), see the green squares. This is to demonstrate that the detection of the true negatives is compromised when a larger value of the % dose criterion is used. Herein, errors not smaller than −5% or 4% are detectable in full (i.e. 0% passing rates).
![]()
Figure 3. The passing rates for the uniform-dose plan in the absence of dose errors. Toggling the option of the measurement uncertainty is illustrated, while other program options are set to our default values. The blue dotted line indicates % dose criterion for which 100% passing rate is achieved with the measurement uncertainty disabled.
![]() (a) (b)
(a) (b)
Figure 4. The passing rates in the uniform-dose plan as a function of the plan renormalization (bottom axis), i.e. error in the dose (top axis). The measured data for γ(1.5%, 1 mm) in (a) for our default program options (black open circles) is shown together with the theoretical prediction (black line). The theoretical prediction for the plan renormalized (by −0.4%) for best match of the centroids is also shown (blue line). Also shown (green squares) is the measured data for γ(3%, 1 mm); (b): effect of the program options on γ(1.5%, 1 mm).
Figure 4(b) contains comparison of the passing rates, γ(1.5%, 1 mm), in the presence of the dose error in the uniform (or quasi-uniform) dose plan for selected program options. The plot for the relative normalization (to the maximum value) can only be plotted for renormalization at or below 100% due to the nature of normalization to the maximum value. Also, the relative-normalization plot does not exhibit any renormalization-type shifts, as the relative data is independent on the dose calibration of the instrument. The relative and the absolute modes yield similar passing rates in the applicable range of the error in dose, although the two plots are shifted w.r.t. each other by about 0.4%. The plot with the “measurement uncertainty” enabled is considerably different from the others. While its shape is similar to the shape of the other plots, the HWHM is about 1% wider. Full detection of the true negatives is achieved for errors not smaller than about ±4%, which is 1% worse than with the “measurement uncertainty” disabled.
3.2. Spatial Error
The passing rates as a function of the mm criterion in the gamma for the dose-gradient plan are plotted in Figure 5 without any misalignment of the ArcCHECK dose distribution w.r.t. the planned distribution. The data was calculated at 0.01% dose criterion (0% is not allowed in the software) in order to separate the error in position from the error in the dose, and our default program options were used. The passing rates increase with increase of the mm criterion, and reach 100% (within the error bar) at or above 1.5 mm. Limitations of use of non-integer values in the mm criterion are addresses in the Discussion. This value of 1.5 mm may be used in routine analysis.
As the primary purpose of using the plan with a gradient is to validate the passing rates in the presence of spatial shifts, we examined the relation between the passing rates and the shift in the plan along the direction of the gradient. In Figure 6(a) we plotted γ(0.01%, 1.5 mm) as a function of the axial shift. 1.5 mm criterion was chosen to match the value where 100% passing rate is obtained in the absence of shifts, and 0.01% criterion was used to match the data from Figure 5. The measured data roughly matches the hat shape of the theoretical prediction. The centroids match within about 0.4 mm. The discrepancy is likely due to a small dose-calibration error, which effectively shifts the dose distribution along the gradient direction. The passing rates vary between 0% and 100%. Similarly to the plot of the passing rates vs. the dose error (see Figure 4), only about 40% (i.e.
![]()
Figure 5. The passing rates in the dose-gradient plan in the absence of shift errors (i.e. errors in position) for the % dose criterion of 0.01%. The dotted line at 1.5 mm indicates the smallest mm criterion for which 100% passing rate is achieved (within the error bar).
![]() (a) (b)
(a) (b)
Figure 6. The passing rates in the dose-gradient plan as a function of the axial shift, i.e. error in the position, for (a): the passing criteria of (0.01%, 1.5 mm) and (b): (1.5%, 1.5 mm). The measured data (solid circles) is shown together with the theoretical predictions (blue lines). The dashed lines are the guide for the eye only.
100% - 60%) of true negatives are detected for −1.5 mm shift, and about 70% (i.e. 100% - 30%) for 1.5 mm shift. All true negatives are detected for shifts equal or over ±3 mm, which is considerably more than the mm criterion of the gamma index.
Figure 6(b) is similar to Figure 6(a), but a different % dose criterion is used: 1.5%, as determined in the previous section. The mm criterion of 1.5 mm is used as in Figure 6(a). These are the suggested criteria for routine QA. The numerically same values of the % dose and the mm criteria are coincidental. The theoretical prediction is also shown, and agreement with the measurements is good. It should be noted that increasing the % dose criterion from 0.01% to 1.5% reduced the sensitivity to detect shift-type errors from about 3 mm to about 4 mm. This is because increasing the dose criterion above 0.01% allows the dose criterion to work together with the mm criterion, see Equation (2). The amount of change in sensitivity to shift errors depends on the slope of the gradient in the dose distribution.
4. Discussion
The tests described in this manuscript are summarized in Table 1 for consequences of errors in the dose and in the position. The tests probing the error in the dose are similar to the tests for the spatial shift, but the varied parameter is different (error in the dose or the geometrical shift), and plans with different dose distributions are used. Tests 1 through 3 quantify the passing rates vs. introduced error. The HWHM and the centroid may be interpreted as measures of accuracy, while the penumbra being a measure of precision. Test 4 is useful to see whether the system is ever capable of reading 100% passing rates. Test 5 and 6 pertain to establishing the optimum criteria for gamma analysis. It should be noted that typically not all of the true negatives are detected in the presence of errors equal in magnitude to the value of the gamma criteria, and such is the case of ArcCHECK too. This observation is consistent with [17] , where the authors note that not all errors are detected for the given choice of the gamma index criteria. Test 6 from Table 1 addresses this problem, and specifies the magnitude of dose and shift errors that are fully detectable, at least for the baseline plans.
The minimum % dose criterion and the minimum mm criterion listed in Table 1 may be used in routine QA. Using smaller values will not allow perfectly-delivered plans to reach 100% passing rate, while using larger values will reduce sensitivity to detect errors. The optimum values of the gamma criteria established herein pertain to the baseline plans, and the passing rates may not reach 100% in QA of complex plans, e.g. VMAT or IMRT plans. In QA of complex clinical plans it might be necessary to accept sub-100% passing rates in QA of clinical plans, e.g. 95%, when using the gamma criteria established in this protocol. One could argue that it is better to increase the gamma criteria in order to only accept plans that pass at 100% rate, e.g. using γ(3%/3 mm). Unfortunately, as seen in Figure 4, this might result in accepting a plan where an unknown (possibly large) fraction of voxels for which disagreement between the measured and the calculated dose approaches −5% (i.e. the minimum fully detectable error for 3% dose criterion), which is a rather large error. On the other hand, choosing (1.5%, 1.5 mm) criteria with acceptance level of e.g. 95% allows only up to 5% of voxels for which the dose error exceeds 3% (i.e. the minimum fully detectable error for 1.5% dose criterion). Even when user chooses increasing the gamma criteria to allow 100% passing rates, the methods presented here could be used to establish the sensitivity to detect delivery errors for the selected values of the gamma criteria.
We did not use MLC in our baseline plans, with the exception of the subfield in the quasi-uniform plan, in order to eliminate errors due to limitations in modeling of the MLC in Eclipse. After all, the shape of the penumbra measured with film differs slightly from the shape planned with Eclipse [19] . We also did not use dynamic arcs in order to eliminate inaccuracy related to gantry movement. Feygelman et al. [1] and Chaswal et al. [20] also evaluated the gamma passing rates upon introduction of errors, but the authors relied on MLC-based or arc-based plans. Recognizing that our baseline plans are simple enough so that the linac is capable of delivering the dose distribution accurately matching the planned distribution, we believe the failure of obtaining 100% passing rates in complex plans (using the criteria from Table 1) in part could be due to limitations of the linac in delivering the dose distribution matching the planned distribution for complex MLC movements.
We opted not to include clinical plans in our protocol. After all, there are several publications listing gamma rates in clinical cases, including a multi-site review by Vieillevigne et al. [17] . Our intention was to develop a
![]()
Table 1. Summary of results upon introduction of errors in dose for the uniform-dose plan and upon introduction of shift errors in the dose-gradient plan delivered to ArcCHECK, and analyzed with our default program options (absolute dose, measurement uncertainty = OFF, Van Dyk = ON, 3D ArcCHECK = OFF).
commissioning-style protocol that could be quickly performed, and would allow selecting % dose and mm criteria that are not specific to the technique (VMAT, IMRT, etc.) or the site. Arguably, it is better to select the gamma criteria from first principles, instead of inspecting numerous clinical plans and assuming that the linac delivers them perfectly. Consequently, we chose to use baseline-type plans instead, and we designed them in a way to make interpretation of the results straightforward. In particular, we constructed these plans to have the theoretical gamma index independent on the location of the detector. In such case the passing rate is either 0% or 100%. As the gamma index depends both on the dose error and the spatial error, it is desirable to test each type of error in a separate step. A uniform-dose plan is an appropriate plan for testing the sensitivity to errors in dose. We used the quasi-uniform plan in the relative-dose mode because it is impossible to introduce dose errors into a uniform-dose plan (in the ideal case, all detectors receive 100% dose independent on the actual value of the dose received). In the relative dose mode with normalization set to the maximum value, only underdose-like discrepancies can be obtained (and tested) by definition.
A plan with a steep dose gradient offers high sensitivity in testing the effect of geometrical errors on the passing rates. We used a plan where the dose gradient is set by 60˚ enhanced dynamic wedges. For simplicity, we only tested the axial direction for shift-type errors. The dose profile of the gradient plan plotted in Figure 1(b) is not entirely linear, which is required for use of Equation (3). To combat this lack of linearity, we constrained the analysis to a ROI, where the dose gradient is approximately constant. For both the uniform and the gradient plan we chose a combination of five fields to accomplish quasi-uniform distribution along the gantry arc. Such solution worked better than a uniform arc, which introduced an artifact of jagged-dose nonuniformity along the arc. An arc-type plan also has a disadvantage of utilizing dynamic gantry movement, making such plan potentially less accurate than a static-fields plan, and our objective was to minimize influence of linac inaccuracies on our results.
Our protocol relies on calculations of the passing rates constrained to the ROIs. When using software that does not allow such, to maintain the constant dose gradient during analysis of the dose gradient plan, one could increase the minimum dose threshold, TH, to about 60%, and shift the ArcCHECK such that the peak of the dose profile (see Figure 2(b)) is outside of the detector array.
Accurate calibration of ArcCHECK is very important in achieving satisfactory results, as any inaccuracy will introduce an error to the measured dose distribution. While our refined calibration procedure differed slightly from the manufacturer’s recommendation, the refined method is consistent with the instructions in the manufacturer's note (ArcCHECK TPS Phantom Setup and Calibration, Sun Nuclear Inc, Melbourne, FL), and is similar to the calibration described by Kozelka [21] . Even though the refined calibration improved the results slightly, it is acceptable to apply the normal calibration only, and follow the remaining parts of our protocol.
The results are not expected to be significantly affected by slight beam asymmetry, because field sizes much smaller than the maximum beam opening were used.
Use of “measurement uncertainty” option during calculations of the gamma indices has been discussed by Nelms et al. [9] . We agree with the authors that application of this parameter unjustifiably biases the passing rates towards higher values. While the passing rates in the uniform-dose plan obtained without introducing any additional dose errors appear to be almost perfect (i.e. 100%) at any value of the % dose criterion (Figure 3), this is at the expense of reducing sensitivity to detect delivery errors. Reduction of the sensitivity to error in the dose when the “measurement uncertainty” is enabled can be observed in Figure 4(b)), where the passing rates are plotted vs. the plan renormalization (equivalent to the error in the dose). Excessively large HWHM of a plotted curve indicates a significant fraction of false positives. Here, the HWHM is about 2.5% with “measurement uncertainty” enabled, which is about 1% larger (i.e. 1% worse) than the value of 1.5% for the other investigated program options. Identifying plans for which the measured dose distribution differs from the planned one (i.e. detection of the true negatives) is the primary objective of any QA of a plan, and therefore we do not recommend enabling “measurement uncertainty”.
Use of fractional values for the criteria in the gamma index requires some clarification. According to the manual, there are no restrictions on the % dose criterion. For the mm‑criterion fractional values are permitted, but their interpretation is limited. Upon searching for the distance to agreement, the grid is interpolated, and the fractional values of the mm criterion are used. When the dose to agreement criterion fails, the full definition of the gamma index is used, and only dose points on the 1 mm square grid are inspected. Consequently, the well- defined values are: 1 mm, 1.5 mm, 2 mm, 2.3 mm, 2.9 mm, 3 mm, etc.
The formalism presented here is applicable to various detector arrays, not just ArcCHECK, as long as the passing rates are calculated based on the gamma index, e.g. film data or 2D data measured with MatriXX. The baseline plans need to be modified accordingly to provide dose distribution appropriate for the given geometry, e.g. the dose distributions need to be uniform or have constant gradient in a plane, not on a cylindrical surface, for measurements with 2D instruments like MatriXX. Use of the formalism in systems which calculate the dose distributions in entire 3D space, not just on a cylindrical surface, is possible too. Again, the plans need to be modified accordingly to provide uniform dose or dose gradient in a 3D structure corresponding to the investigated detector array. The parameters equivalent to those listed in Table 1 might help in deciding whether a given instrument is accurate enough for the particular purpose. For example, an instrument with the optimum % dose criterion of 4% probably would not be good enough as the primary QA check, but might be sufficient as a secondary check if such was required.
The recommended workflow for commissioning-style analysis (for ArcCHECK) is as follows: After calibration of the instrument (on the same day as the subsequent measurements), deliver the uniform-dose plan when absolute-dose measurements are desired for routine QA, or the quasi-uniform dose plan for relative-dose measurements. Decide which other program options will be used, and we recommend disabling the “measurement uncertainty”. Inspect the dependence of the passing rates on the %dose criterion (Figure 3), and identify the smallest %dose for which 100% rate is achieved within the error bar. This is the value recommended for routine QA. Using this just established value of the %dose together with 1 mm for the mm criterion, plot the passing rates as a function of the plan renormalization to identify the minimum fully detectable dose error, i.e. the greater of the smallest (in terms of the absolute value) negative dose error and the smallest positive dose error for which the passing rate is 0% within the error bars (Figure 4(a)). Compare the results to the theoretical prediction, and inspect the values of the centroid, the HWHM and the penumbra. Next, deliver the plan with the uniform dose gradient, and identify the smallest mm criterion allowing the passing rates to reach 100% within the error bar (Figure 5). This value is recommended for routine QA in combination with the %dose criterion established above. Plot the passing rates as a function of the introduced axial shift (Figure 6(a)) for 0.01% %dose criterion and the mm criterion established above. Note the smallest fully-detectable shift error, i.e. the greater of the smallest negative mm shift and the smallest positive mm shift for which the passing rate is 0%. Inspect the centroid, the HWHM and the penumbra. Compare the passing rates with introduced shift error to the theoretical prediction (which for the %dose criterion of 0.01% is 100% when the shift does not exceed the mm criterion and 0% otherwise. The error bars mentioned above can be established as the standard deviation of the mean of several measurements (with the setup redone before each).
5. Conclusion
Instead of analyzing a large number of clinical plans, we performed only two measurements with baseline-type plans to identify the optimum criteria for gamma analysis of dose distributions measured with a detector array (ArcCHECK), see the recommended workflow described in Discussion. We validated the corresponding passing rates against the theoretical prediction. We used a uniform (or quasi-uniform) dose plan to examine the influence of the dose error on the gamma rates, and a steep gradient plan to test the influence of shifts on the gamma rates. We identified a set of single-number parameters that quantify performance of detector arrays, and we identified optimum gamma-index criteria from the baseline plans. We observed that introduction of delivery errors equal in magnitude to the corresponding criterion (% or mm) did not guarantee detection of artificially introduced errors by all the detectors of the array. Instead, we determined the minimum errors that would be detected by all detectors of the array. We discussed the impact of selected program options (in SNC Patient) on the passing rates. This protocol can be applied to other detector arrays, provided the baseline plans are modified as dictated by the topology of the detector array.