Spectral Analysis for Fractional Hydrogen Atom Equation

Erdal Bas^*, Funda Metin

Department of Mathematics, Faculty of Science, Elazig, Turkey.

DOI: 10.4236/apm.2015.513070                

Abstract

In this paper, spectral analysis of fractional Sturm Liouville problem defined on (0, 1], having the singularity of type  at zero and researched the fundamental properties of the eigenfunctions and eigenvalues for the operator. We show that the eigenvalues and eigenfunctions of the problem are real and orthogonal, respectively.

Keywords

Sturm-Liouville, Fractional, Hydrogen Atom, Singular, Spectral

1. Introduction

Fractional calculus have been available and applicable to various fields of science, the investigation of the theory of fractional differential equations has only been started recently. At the same time, fractional differential equations have great interest due to their numerous applications in many fields of science, such as physics, mechanics, chemistry, finance, electromagnetics, acoustics, viscoelasticity, electrochemistry, economy, etc. So far, there have been several fundamental works on the fractional derivative and fractional differential equations, written by Miller and Ross [1] Podlubny [2] Kilbas, Srivastava and Trujillo [3] .

In recent years, fractional Sturm-Liouville problems have been studied and these studies, which the eigenvalues and eigenfunctions associated to these operators and also theirs properties, have been published by M. Klimek and O. P. Argawal [4] [7] . Furthermore, there are a lot of studies in this topic [4] -[13] .

Sturm-Liouville problems have been studied for over two hundred years. The great progress has been made related to spectral theory. And this topic has an increasing interest for years from different points of view [14] - [23] .

2. Preliminaries

Firstly, we consider singular Sturm-Liouville equation

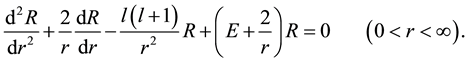
In quantum mechanics the study of the energy levels of the hydrogen atom leads to this equation [5] . Where R is the distance of the mass center to the origin. l is positive integer, a is real number E is energy constant and r is the distance between the nucleus with the electron.

Substitution 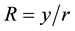reduces above equation to the form

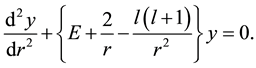
In most cases we took the reference potential to be

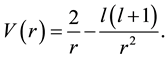
When 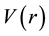is defined by last differential equation it contains a centripetal and Coulomb part, the usual singularities of the nuclear problem. We consider the following fractional singular Sturm-Liouville problem for hydrogen atom equation

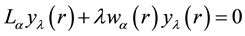
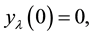
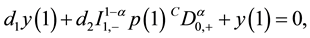
where the fractional order 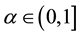and is defined as

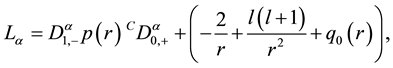
where 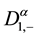and refers to the Riemann-Liouville and Caputo fractional derivative defined below by definition 2, respectively. The main theoretical result of the paper is prove spectral properties fractional singular Sturm-Liouville problem for hydrogen atom equation.

Definition 1. [2] Let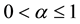. The left-sided and respectively right-sided Riemann-Liouville integrals of order are given by the formulas

(1)

(2)

where denotes the gamma function.

Definition 2. [2] Let . The left-sided and respectively right-sided Riemann-Liouville derivatives of order are defined as

(3)

(4)

Analogous formulas yield the left and right-sided Caputo derivatives of order:

(5)

(6)

Property 3. [7] The fractional differential operators defined in (3)-(6) satisfy the following identities:

(7)

(8)

Property 4. [7] Assume and. Then the following relations

(9)

hold for any . Furthermore, the integral operators defined in (1), (2) satisfy the following semi-group properties.

Now, let’s take up a fractional Sturm-Liouville problem for hydrogen atom equation.

3. A Singular Fractional Sturm-Liouville Problem for Hydrogen Atom Equation

Let’s denote a singular fractional Sturm-Liouville problem for hydrogen atom equation with the differential part containing the left and right-sided derivatives. Let’s use the form of the integration by parts formulas (7) and (8) for this new approximation. Main properties of eigenfunctions and eigenvalues in the theory of classical Sturm- Liouville problems are related to the integration by parts formula for the appear and the essential pairs are the left Riemann-Liouville derivative with the right Caputo derivative and the right Riemann-Liouville derivative with the left Caputo one.

Definition 5. For. Fractional hydrogen atom operator is written as

(10)

consider the fractional hydrogen atom equation

(11)

where and p, q are real valued continuous functions in interval (0, 1]. The boundary conditions for the operator L are the following:

(12)

(13)

where . The fractional boundary-value problem (11)-(13) is fractional Sturm-Liouville problem for hydrogen atom operator.

Theorem 6. Fractional hydrogen operator is self-adjoint on (0, 1].

Proof. Let us consider the following equation

Considering property 3 to the first integral in the last equation, we obtain the identity

(14)

Similarly, we obtain

(15)

The right hand sides of the Equations (14) and (15) are equal hence we may see that the left sides are equal that is

Therefore, The proof is completed.

Theorem 7. The eigenvalues of fractional hydrogen atom operator (11)-(13) are real.

Proof. Let us observe that following relation results from property (3)

(16)

Suppose that is the eigenvalue for (11)-(13) corresponding to eigenfunction y the following equalities are satisfy y and its complex conjugate

(17)

(18)

(19)

(20)

(21)

(22)

where We multiply Equation (17) by function and (20) by function y respectively and subtract:

Now, we integrate over interval (0, 1] and applying relation (16) we note that the right-hand side of the integrated equality contains only boundary terms:

by virtue of the boundary conditions (18), (19), (21), (22), we find

and because y is a non-trivial solution and , it easily seen that .

Theorem 8. The eigenfunctions corresponding to distinct eigenvalues of fractional hydrogen atom operator (11)-(13) are orthogonal weight function on (0, 1] that is

Proof. We have by assumptions fractional Sturm-Liouville for hydrogen atom operator fulfilled by two different eigenvalues and the respective eigenfunctions , in that case

(23)

(24)

(25)

(26)

(27)

(28)

we multiply Equation (23) by function and (26) by function respectively and subtract:

Integrating over interval (0, 1] and applying relation (16) we note that the right-hand side of the integrated equality contains only boundary terms:

Using the boundary conditions (24), (25), (27), (28), we find that

where . The proof is completed.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Miller, K.S. and Ross, B. (1993) An Introduction to the Fractional Calculus and Fractional Differential Equations. John Wiley and Sons, New York.
[2]	Podlubny, I. (1999) Fractional Differential Equations. Academic Press, San Diego.
[3]	Kilbas, A.A., Srivastava, H.M. and Trujillo, J.J. (2006) Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam.
[4]	Klimek, M. (2009) On Solutions of Linear Fractional Differential Equations of a Variational Type. The Publishing Office of Czestochowa, University of Technology, Czestochowa.
[5]	Al-Mdallal, Q.M. (2009) An Efficient Method for Solving Fractional Sturm-Liouville Problems. Chaos Solitons and Fractals, 40, 183-189. http://dx.doi.org/10.1016/j.chaos.2007.07.041
[6]	Erturk, V.S. (2011) Computing Eigenelements of Sturm-Liouville Problems of Fractional Order via Fractional Differential Transform Method. Mathematical and Computational Applications, 16, 712-720.
[7]	Klimek, M. and Argawal, O.P. (2012) On a Regular Fractional Sturm-Liouville Problem with Derivatives of Order in (0,1). Proceedings of the 13th International Carpathian Control Conference, Vysoke Tatry (Podbanske), Slovakia, 28-31 May 2012. http://dx.doi.org/10.1109/carpathiancc.2012.6228655
[8]	Baleanu, D., Octavian, M.G. and Agarwal, P.R. (2011) Asymptotic Integration of (1+Alpha)-Order Fractional Differential Equations. Computers & Mathematics with Applications, 62-63, 1492-1500. http://dx.doi.org/10.1016/j.camwa.2011.03.021
[9]	Yilmazer, R. (2010) N-Fractional Calculus Operator N^{μ} Method to a Modified Hydrogen Atom Equation. Mathematical Communications, 15, 489-501.
[10]	Bas, E. (2013) Fundamental Spectral Theory of Fractional Singular Sturm-Liouville Operator. Journal of Function Spaces and Applications, Article ID: 915830.
[11]	Samko, S.G., Kilbass, A.A. and Marichev, O.I. (1993) Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach Science Publishers, Philadelphia.
[12]	Hilfer, R. (2000) Applications of Fractional Calculus in Physics. World Scientific, Singapore.
[13]	Carpinteri, A. and Mainardi, F., Eds. (1998) Fractals and Fractional Calculus in Continum Mechanics. Springer-Verlag, Telos.
[14]	Johnson, R.S. (2006) An Introduction to Sturm-Liouville Theory. University of Newcastle, Upon Tyne Publishing, Newcastle upon Tyne.
[15]	Zettl, A. (2005) Sturm-Liouville Theory, Mathematical Surveys and Monographs. Volume 121, American Mathematical Society, Providence.
[16]	Amrein, W.O., Hinz, A.M. and Pearson, D.B. (2005) Sturm-Liouville Theory: Past and Present. Birkhauser, Basel, Switzerland.
[17]	Panakhov, E.S. and Yilmazer, R. (2012) A Hochstadt-Lieberman Theorem for the Hydrogen Atom Equation. Computational & Applied Mathematics, 11, 74-80.
[18]	Levitan, B.M. and Sargsjan, I.S. (1975) Introduction to Spectral Theory: Self Adjoint Ordinary Differential Operators. American Mathematical Society, Providence.
[19]	Qi, J. and Chen, S. (2011) Eigenvalue Problems of the Model from Nonlocal Continuum Mechanics. Journal of Mathematical Physics, 52, Article ID: 073516. http://dx.doi.org/10.1063/1.3610673
[20]	Bas, E., Panakhov, E. and Yilmazer, R. (2013) The Uniqueness Theorem for Hydrogen Atom Equation. TWMS Journal of Pure and Applied Mathematics, 4, 20-28.
[21]	West, B.J., Bologna, M. and Grigolini, P. (2003) Physics of Fractal Operators. Springer Verlag, New York. http://dx.doi.org/10.1007/978-0-387-21746-8
[22]	Atanackovic, T.M. and Stankovic, B. (2009) Generalized Wave Equation in Nonlocal Elasticity. Acta Mechanica, 208, 1-10. http://dx.doi.org/10.1007/s00707-008-0120-9
[23]	Granas, A. and Dugundji, J. (2003) Fixed Point Theory. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-0-387-21593-8