Hall Current Effects on Unsteady MHD Flow in a Rotating Parallel Plate Channel Bound-ed by Porous Bed on the Lower Half—Darcy Lapwood Model ()
1. Introduction
Flow of a viscous fluid in rotating channels is of considerable importance due to the occurrence of various natural phenomena and for its application in various technological situations which are governed by the action of Coriolis force. The broad subjects of oceanography, meteorology, atmospheric science and limnology all contain some important and essential features of rotating fluids. The viscous fluid flow problems in rotating medium under different conditions and configurations are investigated by many researchers in the past to analyze various aspects of the problem. The study of simultaneous effects of rotation and magnetic field on the fluid flow problems of a viscous incompressible electrically conducting fluid may find applications in the areas of geophysics, astrophysics and fluid engineering. An order of magnitude analysis shows that, in the basic field equations, the effects of Coriolis force are more significant as compared to that of inertial and viscous forces. Furthermore, it maybe noted that Coriolis and magnetohydrodynamic forces are comparable in magnitude and Coriolis force induces secondary flow in the flow-field.
A large variety of processes of interest to industry and society involve the flow of fluids through porous media. Examples include the use of filtration to purify water and treat sewage, membranes to separate gases, the chemical reactors having porous catalysts supports. The mathematical modelling and simulation of the flow of fluids through porous media are important for designing and controlling a number of industrial processes including the production of fluids from underground reservoir and remediation of underground water resources. The simulation of flow is carried out using constitutive and conservative relations based on a macroscopic representation of porous media. There is a considerable interest in the recent years in the study of flow past a naturally permeable bed, with appropriate boundary conditions at a naturally permeable boundary. The usual conditions are: the normal flux is continuous and the tangential velocity is zero. The former is completely satisfactory but the latter is clearly only an approximation. As an alternative to these no-slip boundary conditions postulated for the first time (Beavers and Joseph [1] ), the slip boundary condition which they had verified experimentally. The existence of the slip at the porous bed, due to the transfer of momentum from the free flow to Darcy flow which sets up the drag, is connected with presence of a very thin boundary layer of stream wise moving fluid just beneath the nominal surface of the permeable material. The fluid in this layer is pulled along by the flow in the channel. Although the experiments were performed by Beavers and Joseph to test the validity of the proposed slip boundary conditions, owing to in adequate apparatus and instruments, the accuracy of experimental results was not sufficient to permit conclusive evaluation of the proposed analytical model although the existence of a slip velocity was confirmed qualitatively.
Later experiments by Beavers, Sparrow and Magnuson [2] , Taylor [3] and Rajashekara [4] further confirmed the existence of the slip at the nominal surface. Saffman [5] gave a rigorous theoretical proof for the existence of the slip at the nominal surface postulated by Beavers and Joseph [1] . Rajasekhar et al. [6] investigated a steady laminar flow of forced convection through a channel having on porous bounding wall. They have taken into account the velocity slip at the surface of the porous medium and the contribution of heat due to viscous dissipation. Although the slip at the nominal surface was established based on the extension of a thin boundary layer just beneath the nominal surface attention was not focused on the analytical determination of the boundary layer thickness. Later Chennabasappa and Ramanna [7] discussed the effect of the thickness of the porous material on the parallel plate channel. Valanis and Sun [8] investigated the Poiseuille flow of fluid with couple stress with Applications to blood flow. Claire Jacobs [9] explained the transient motions produced by disks oscillating about a state of rigid rotation. Debnath [10] gave the exact solutions of the unsteady hydrodynamic and hydro magnetic boundary layer equations in a rotating fluid system. Blood flow through narrow tube with periodic body acceleration in the presence of magnetic field and its applications to cardiovascular diseases was discussed by Rani [11] . Also Rathod et al. [12] discussed blood flow through stenosed inclined tubes with periodic body acceleration in the presence of magnetic field and its applications to cardiovascular diseases. Rajasekhara [4] has performed the experiments to study the laminar flow characteristics in a composite channel considering Poiseuille flow, Couette flow and free surface flow. The aim of his experimental study was to determine the values of the slip parameter lower than that of Beavers & Joseph [1] . Such lower values are of importance in the design of porous bearings. Auxiliary experiments were also conducted to measure the values of k, the permeability of the porous medium. His experiments showed that for aparticular porous materials namely natural sand α = 0.01 as compared with α = 0.1 of Beavers & Joseph [1] for foametal, and is independent of the depth of flow above bed. His experimental results were found to be in fair agreement with the analytical model which contains slip velocity at the permeable surface, except the mass flow rate which shows a slight deviation between experimental and theoretical data. Rudraiah and Veerabhadraiah [13] have pointed out that this deviation may be due to the neglecting of buoyancy force. Rao and Krishna [14] discussed the Hall effects on free and forced convective flow in a rotating channel. Rao et al. [15] investigated the Hall effects on the Stokes and Ekman problems in Magneto Hydro Dynamics. Sarojamma and Krishna [16] studied transient hydromagnetic convective flow in a rotating channel with porous boundaries. Later Sasthry [17] studied the effect of the thickness of the porous lining on one side of the plate flow through a rotating parallel plate channel. And he discussed the flow in a rotating parallel plate channel with porous lining on both sides. Siva Prasad [18] discussed convection flows through planar channels in Magneto Hydro Dynamics.
Recently M. V. Krishna et al. [19] discussed the unsteady flow of an incompressible viscous fluid in a rotating parallel plate channel bounded on one side by a porous bed under the influence of a uniform transverse magnetic field making use of Darcy Lapwood model. D. V. Krishna et al. [20] discussed the unsteady hydromagnetic flow of an incompressible viscous fluid in a rotating parallel plate channel with porous lining under theinfluence of uniform transverse magnetic field normal to the channel and it was extended by M.V. Krishna et al. [21] . M. V. Krishna et al. [22] studied the steady hydro magnetic flow of a couple stress fluid through a composite medium in a rotating parallel plate channel with porous bed on the lower half subjected to subjected to normal to the channel and extended the problem taking hall current into account by M. V. Krishna et al. [23] . M. V. Krishna and S. G. Malashetty [24] discussed the unsteady flow of an in compressible electrically conducting second grade fluid in rigidly rotating parallel plate channel bounded below by a sparsely packed porousbed subjected to normal to the channel and extended the problem taking hall current into account by M. Veera Krishna and S. G. Malashetty [25] . Mention may be made of the research studies of Greenspan and Howard [26] , Holton [27] , Walin [28] , Siegman [29] , Puri [30] , Puri and Kulshrestha [31] , Mazumder [32] , Ganapathy [33] , Hayat and Hutter [34] and Hayat et al. [35] on MHD flows through rotating channels.
Motivated in view of the above discussions, in this paper, we discuss the unsteady flow of an incompressible viscous fluid in a rotating parallel plate channel bounded on one side by a porous bed under the influence of a uniform transverse magnetic field taking hall current into account. The perturbations are created by a constant pressure gradient along the plates in addition to the non-torsional oscillations of the upper plate. The flow in the clean fluid region is governed by Navier-Stoke’s equations while in the porous bed the equations are based on Darcy-Lapwood model.
2. Formulation and Solution of the Problem
We consider the unsteady flow of an in compressible viscous fluid in a rotating parallel plate channel bounded on one side by a porous bed subjected to a uniform transverse magnetic field normal to the channel. In the initial undisturbed state both the plates and the fluid rotate with the same angular velocity . At t > 0 the fluid is driven by a constant pressure gradient parallel to the channel walls and in addition the upper plate perform non- torsional oscillations in its own plane.
. At t > 0 the fluid is driven by a constant pressure gradient parallel to the channel walls and in addition the upper plate perform non- torsional oscillations in its own plane.
We choose a Cartesian system O(x,y,z) such that the boundary walls are at z = 0 and z = l. Z-axis being the axis of rotation of the plates. The fluid medium consists of two zones namely zone 1and zone 2. Zone 1 consists of clean fluid governed by Navier-Stokes equations and zone 2 corresponds to the flow through porous bed governed by Darcy-Lapwood equations. At the interface the fluid satisfies the continuity condition of velocity and shear stress. The unsteady hydromagnetic equations governing the incompressible viscous fluid in zone 1 under the influence of transverse magnetic field with reference to a frame rotating with a constant angular velocity 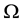 are
are
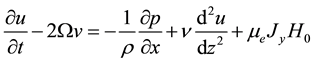 (2.1)
(2.1)
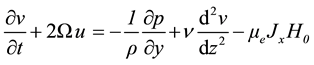 (2.2)
(2.2)
The Darcy-Lapwood equations governing the flow through porous medium with respect to the rotating frame zone 2
 (2.3)
(2.3)
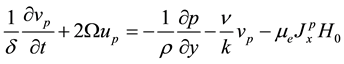 (2.4)
(2.4)
where (u, v) and (up, vp) are velocity components along O(x, y) directions respectively. ρ the density of the fluid , 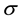 the conductivity of the medium, µe the magnetic permeability,
the conductivity of the medium, µe the magnetic permeability, 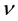 the coefficient of kinematic viscosity,
the coefficient of kinematic viscosity, 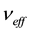 the coefficient of effective kinematic viscosity, k the permeability of the medium,
the coefficient of effective kinematic viscosity, k the permeability of the medium, 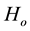 is the applied magnetic field and
is the applied magnetic field and 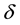 is the porosity. Since the plates extends to infinity along x and y directions, all the physical quantities except the pressure depend on z and t alone. Hence u, v and up, vp are function of z and t alone and hence the respective equations of continuity are trivially satisfied. When the strength of the magnetic field is very large, the generalized Ohm’s law is modified to include the Hall current, so that
is the porosity. Since the plates extends to infinity along x and y directions, all the physical quantities except the pressure depend on z and t alone. Hence u, v and up, vp are function of z and t alone and hence the respective equations of continuity are trivially satisfied. When the strength of the magnetic field is very large, the generalized Ohm’s law is modified to include the Hall current, so that
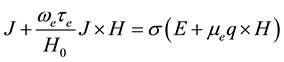 (2.5)
(2.5)
where q is the velocity vector, H is the magnetic field intensity vector, E is the electric field, J is the current density vector, 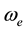 is the cyclotron frequency,
is the cyclotron frequency, 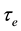 is the electron collision time,
is the electron collision time, 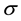 is the fluid conductivity and
is the fluid conductivity and ![]() is the magnetic permeability. In Equation (2.5) the electron pressure gradient, the ion-slip and thermo-electric effects are neglected. We also assume that the electric field E = 0 under assumptions reduces to
is the magnetic permeability. In Equation (2.5) the electron pressure gradient, the ion-slip and thermo-electric effects are neglected. We also assume that the electric field E = 0 under assumptions reduces to
![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
where ![]() is the hall parameter.
is the hall parameter.
On solving Equations (2.6) and (2.7) we obtain
![]() (2.8)
(2.8)
![]() (2.9)
(2.9)
and similarly we obtain
![]() (2.10)
(2.10)
![]() (2.11)
(2.11)
Using the Equations (2.8) and (2.9) the equations of the motion with reference to rotating frame zone 1 are given by
![]() (2.12)
(2.12)
![]() (2.13)
(2.13)
The Darcy-Lapwood equations governing the flow through porous medium with respect to the rotating frame zone 2 are given by
![]() (2.14)
(2.14)
![]() (2.15)
(2.15)
Let ![]()
Now combining Equations (2.12) and (2.13), we obtain
![]() (2.16)
(2.16)
and combining Equations (2.14) and (2.15) , we obtain
![]() (2.17)
(2.17)
The boundary and initial conditions are
![]() (2.18)
(2.18)
![]() (2.19)
(2.19)
![]() (2.20)
(2.20)
At the interface we allow slip governed by Beaver-Joseph condition
(Dimensional form)
![]() (2.21)
(2.21)
where ![]() is the slip velocity and
is the slip velocity and ![]() is the non-dimensional number (slip parameter). Also at the interface,
is the non-dimensional number (slip parameter). Also at the interface,
![]() (2.22)
(2.22)
We introduce the following non dimensional variables are
![]()
Introducing these non-dimensional variables, the governing non-dimensional equations are (dropping the asterisks)
![]() (2.23)
(2.23)
![]() (2.24)
(2.24)
where, ![]() is the Hartmann number,
is the Hartmann number, ![]() is the Inverse Darcy Parameter,
is the Inverse Darcy Parameter, ![]() is the
is the
Ekman number, ![]() is the hall parameter,
is the hall parameter, ![]() is the applied pressure gradient
is the applied pressure gradient
The corresponding non-dimensional boundary and initial conditions are
![]() (2.25)
(2.25)
![]() (2.26)
(2.26)
![]() (2.27)
(2.27)
The Beaver-Joseph condition reduces to
![]() (2.28)
(2.28)
The interfacial condition is
![]() (2.29)
(2.29)
Taking Laplace transforms of Equations (2.23) and (2.24) using initial condition (2.27) the governing equations in terms of the transformed variable reduces to
![]() (2.30)
(2.30)
The relevant transformed boundary condition is
![]() (2.31)
(2.31)
And
![]() (2.32)
(2.32)
The transformed Beavers-Joseph Condition and relevant boundary conditions are
![]() (2.33)
(2.33)
Solving Equation (2.30) subjected to the condition (2.31), we get
![]() (2.34)
(2.34)
where ![]()
![]() (2.35)
(2.35)
From Equation (2.32)
![]() (2.36)
(2.36)
where, ![]()
and from (2.34)
![]() (2.37)
(2.37)
Equating Equations (2.37) and Beaver-Joseph condition (2.33) using (2.36) we get
![]() (2.38)
(2.38)
From interfacial conditions (2.29) and (2.38) reduces to
![]() (2.39)
(2.39)
Solving Equations (2.35) and (2.39) we obtain,
![]() (2.40)
(2.40)
and
![]()
(2.41)
Taking inverse Laplace transforms to the Equations (2.36), (2.40) and (2.41), we obtain
![]() (2.42)
(2.42)
![]()
![]() (2.43)
(2.43)
![]()
![]() (2.44)
(2.44)
The shear stresses on the upper plate and lower plate are given by
![]() and
and![]()
We also determine the mass flux by the formula,
![]()
3. Results and Discussion
The porous bed is bounded by the lower plate in the rotating channel which executes non-torsional oscillations. The clean fluid region (zone 1) is governed by the Navier-Stokes equations and is bounded by the upper plate of the channel at rest relative to the rotating frame. The governing Darcy-Lapwood model equation in the porous medium being linear cannot satisfy more than one condition. Hence for compatibility we introduce an interfacial condition namely the Beavers-Joseph condition (B-J Condition) which allows the fluid to slip with velocity qB at the interface. We combine the equations in both clean fluid region as well as the porous region. The equation governing the flow in the clean fluid region (zone 1) reduced to a second order partial differential equation for the dependent variable![]() , which is solved by using Laplace transform method. The equation governing the flow in porous bed (zone 2) is a first order differential equation for the dependent variable
, which is solved by using Laplace transform method. The equation governing the flow in porous bed (zone 2) is a first order differential equation for the dependent variable![]() , which reduces to an algebraic equation on taking the Laplace transform. On taking the inverse Laplace trans- form the solution for the combined velocity q consists of the steady state terms, the quasi steady state terms and
, which reduces to an algebraic equation on taking the Laplace transform. On taking the inverse Laplace trans- form the solution for the combined velocity q consists of the steady state terms, the quasi steady state terms and
the transient terms which ultimately decay in times ![]() i.e.,
i.e.,![]() .
.
Once the transient terms decay the expression corresponding steady and oscillatory flows are given by
![]()
The transient term in qp decay at time![]() .
.
The ultimate Darcy velocity qp in the porous bed after the decay of the transient term is
![]()
The slip velocity qB has been calculated using B-J condition (2.33) and is governed by the expression (2.44).The velocity profiles for u and v in the clean fluid region have been drawn Figures 1-16 for the variations in the governing parameters and fixing the other parameters![]() . Figures 1-4 corresponds to these profiles for the thickness of porous bed is small while Figures 5-8 corresponds to these profiles when the thickness of the porous bed is large. We notice that u enhances with E or m and reduces with M or D−1 in either case of smaller and larger thickness of porous bed (Figures 1-8). The magnitude of the velocity component v enhances with E but reduces with M, m and D−1 in either cases of smaller and larger thickness of porous bed (Figures 9-16). The resultant velocity however enhances with E and m and reduces with M and D−1 irrespective of the thickness of the porous bed and is always directed away from the central axis of the channel with phase difference greater than
. Figures 1-4 corresponds to these profiles for the thickness of porous bed is small while Figures 5-8 corresponds to these profiles when the thickness of the porous bed is large. We notice that u enhances with E or m and reduces with M or D−1 in either case of smaller and larger thickness of porous bed (Figures 1-8). The magnitude of the velocity component v enhances with E but reduces with M, m and D−1 in either cases of smaller and larger thickness of porous bed (Figures 9-16). The resultant velocity however enhances with E and m and reduces with M and D−1 irrespective of the thickness of the porous bed and is always directed away from the central axis of the channel with phase difference greater than ![]() from the direction of the imposed pressure gradient tabulated. The slip velocities uB and vB have been calculated at tabulated in the Table 1 and Table 2 for the different variations in the governing parameters. The slip velocity uB enhances with its magnitude with increasing in E, m, M and D−1 for the smaller and larger thickness of porous bed (Table 1). The slip velocity vB enhances with its magnitude increase in E or m while reduces with increases in M (or) D−1 for the irrespective thickness of porous bed (Table 2).
from the direction of the imposed pressure gradient tabulated. The slip velocities uB and vB have been calculated at tabulated in the Table 1 and Table 2 for the different variations in the governing parameters. The slip velocity uB enhances with its magnitude with increasing in E, m, M and D−1 for the smaller and larger thickness of porous bed (Table 1). The slip velocity vB enhances with its magnitude increase in E or m while reduces with increases in M (or) D−1 for the irrespective thickness of porous bed (Table 2).
The shear stresses of the upper and lower plate are evaluated and tabulated in Tables 3-6. Table 3 indicates ![]() for variations in the governing parameters in case of smaller and larger thickness of the porous bed. Table 4 represents to these variations for
for variations in the governing parameters in case of smaller and larger thickness of the porous bed. Table 4 represents to these variations for ![]() for the upper plate. We find that
for the upper plate. We find that ![]() and
and ![]() reduces with E or m irrespective of thickness (0.2 & 0.5), and an increasing in M or D−1 enhances
reduces with E or m irrespective of thickness (0.2 & 0.5), and an increasing in M or D−1 enhances ![]() and
and ![]() reduces irrespective of thickness (0.2 & 0.5). On the lower plate Table 5 indicates that for variations in governing parameters in case of smaller and larger thickness of porous bed for
reduces irrespective of thickness (0.2 & 0.5). On the lower plate Table 5 indicates that for variations in governing parameters in case of smaller and larger thickness of porous bed for ![]() and the Table 6 represent to these variations for
and the Table 6 represent to these variations for![]() . We notice that an increase E, m, M or D−1 enhances
. We notice that an increase E, m, M or D−1 enhances ![]() however
however ![]() reduces with increase in M or D−1 enhances with increase in E or m. This is true in either case of smaller and larger thickness of porous bed (Table 5 & Table 6). The Table 7 corresponds to the behaviour of mass flux and we notice that which increases with E or m but reduces with increase in M or D−1 in either case of the thickness of porous bed.
reduces with increase in M or D−1 enhances with increase in E or m. This is true in either case of smaller and larger thickness of porous bed (Table 5 & Table 6). The Table 7 corresponds to the behaviour of mass flux and we notice that which increases with E or m but reduces with increase in M or D−1 in either case of the thickness of porous bed.
4. Graphs and Tables
4.1. Velocity Profiles for u & v When the Thickness of the Porous Bed (h = 0.2) Is Small
![]()
Figure 1. The velocity profile for u against E with M = 2, D−1 = 1000, m = 1.
![]()
Figure 2. The velocity profile for v against E with M = 2, D−1 = 1000, m = 1.
![]()
Figure 3. The velocity profile for u against M with E = 0.01, D−1 = 1000, m = 1.
![]()
Figure 4. The velocity profile for v against M with E = 0.01, D−1 = 1000, m = 1.
![]()
Figure 5. The velocity profile for u against D−1 with E = 0.01, M = 2, m = 1.
![]()
Figure 6. The velocity profile for v against D−1 with E = 0.01, M = 2, m = 1.
![]()
Figure 7. The velocity profile for u against m with E = 0.01, M = 2, D−1 = 1000.
![]()
Figure 8. The velocity profile for v against m with E = 0.01, M = 2, D−1 = 1000.
4.2. Velocity Profiles for u & v When the Thickness of the Porous Bed (h = 0.5) Is Large
![]()
Figure 9. The velocity profile for u against E with M = 2, D−1 = 1000, m = 1.
![]()
Figure 10. The velocity profile for v against E with M = 2, D−1 = 1000, m = 1.
![]()
Figure 11. The velocity profile for u against M with E = 0.01, D−1 = 1000, m = 1.
![]()
Figure 12. The velocity profile for v against M with E = 0.01, D−1 = 1000, m = 1.
![]()
Figure 13. The velocity profile for u against D−1 with E = 0.01, M = 2, m = 1.
![]()
Figure 14. The velocity profile for v against D−1 with E = 0.01, M = 2, m = 1.
![]()
Figure 15. The velocity profile for u against m with E = 0.01, M = 2, D−1 = 1000.
![]()
Figure 16. The velocity profile for v against m with E = 0.01, M = 2, D−1 = 1000.
![]()
Table 3. The shear stress ![]() on the upper plate.
on the upper plate.
![]()
Table 4. The shear stress ![]() on the upper plate.
on the upper plate.
![]()
Table 5. The shear stress ![]() on the lower plate.
on the lower plate.
![]()
Table 6. The shear stress ![]() on the lower plate.
on the lower plate.
5. Conclusions
We discussed the unsteady flow of an incompressible viscous fluid in a rotating parallel plate channel bounded on one side by a porous bed under the influence of a uniform transverse magnetic field taking hall current into account. The conclusions are made as the following:
1) The slip velocity qB has been calculated using B-J condition. The slip velocity uB enhances with its magnitude with increasing in E, M and D−1 for the smaller and larger thickness of porous bed. The slip velocity vB enhances with its magnitude increase in E or m while reduces with increases in M (or) D−1 for the irrespective thickness of porous bed.
2) The magnitude of the velocity component u enhances with E or m and reduces with M or D−1 in either case of smaller and larger thickness of porous bed.
3) The magnitude of the velocity component v enhances with E but reduces with M, m and D−1 in either cases of smaller and larger thickness of porous bed.
4) The resultant velocity however enhances with E and m and reduces with M and D−1 irrespective of the thickness of the porous bed and is always directed away from the central axis of the channel with phase difference greater than ![]() from the direction of the imposed pressure gradient.
from the direction of the imposed pressure gradient.
5) The magnitude of the stresses ![]() and
and ![]() reduces with E or m irrespective of thickness and an increasing in M or D−1 enhances
reduces with E or m irrespective of thickness and an increasing in M or D−1 enhances ![]() and
and ![]() reduces irrespective of thickness on the lower plate for variations in governing parameters.
reduces irrespective of thickness on the lower plate for variations in governing parameters.
6) An increase E, M or D−1 enhances ![]() however
however ![]() reduces with increase in M or D−1 enhances with increase in E. This is true in either case of smaller and larger thickness of porous bed.
reduces with increase in M or D−1 enhances with increase in E. This is true in either case of smaller and larger thickness of porous bed.
7) The behaviour of mass flux and we notice that which increases with E or m but reduces with increase in M or D−1 in either case of the thickness of porous bed.
Appendix
![]()
![]()
![]()
NOTES
*Corresponding author.