Random Matrix Approach to Correlation Matrix of Financial Data (Mexican Stock Market Case) ()
1. Introduction
Random Matrix Theory has been one of those mathematical discoveries or inventions from physicists due to their need to solve problems for physics. This theory has been a useful tool to recognize chaotic patterns in com- plex systems, and this tool is useful in the procedure of null hypothesis when it is compared with empirical data matrices for which correlation is clear [1] . The main idea to use properly this tool would be taking data from a complex system, building a correlation matrix with these data by time series method for real entries and finally comparing its spectrum with the spectrum of a random matrix. The deviation among both spectra will provide an idea of how “chaotic” (in a statistical sense) the system would be; if this deviation is small with respect to other standards, and then mathematical chaos would be involved in our complex system. We do not use the classic chaos concept known from physics for which chaos or chaotic systems are understood as non-integrable dynamical systems. Although mathematical chaos and physical chaos in dynamical systems, and the integrability have different definitions, they converge physically and philosophically. Speaking in technical terms, applications of random matrix theory have been enlisted from historical origins of it. The first application of this theory was born from need of a tool for several quantum states for nucleus study developed by L. Landau density about matrices with hamiltonian component entries [2] . Lately the method described before, was used for a several kind of complex systems such as brain signal data, stock market data (see also [3] ), communications and signals in the sense of antenna systems. It is obvious that this method can be applied (perhaps with some restrictions due to the inherent nature of systems) to every complex system in order to find out if there is some chaotic property in mathematical sense for this system. In this paper we present a financial application with some risk theory involved.
We will refer to Random Matrix Theory as RMT from now on. RMT has been a great eye-opener since its development for nuclear physics applications. As it is well known in literature, atomic and nuclear complex systems were studied successfully with RMT’s help. RMT is one of branches in mathematics for which its development is owned by physics due to its need. A random matrix is defined as a (square or non-square) matrix with random entries. The most interesting part for analysis in RMT is the eigenvalue spectrum of matrices with random entries. This led us to analyze the distributions of eigenvalues and its reciprocal eigenvalues and then focus our attention on integration over these eigenvalue distributions. On the other hand, a cross correlation matrix is a matrix for which its entries are made of with time series of a certain set of a probably correlated data. Eigenvalues of cross correlated data matrices can be analyzed in the same way as for random matrices. High technology developments on statics and complex systems analysis, chaos theory and random matrices, lead us forward in the possible innovation of these tools inside a lot of knowledge fields. These fields vary widely; there have been developed applications for quantum and skew-quantum chaos theory, biological complex systems, weather and finally economy and finance. Applications of this field are made in this article. Just as it was comment at the abstract, we took a database of financial data from Mexican stock market taken from [4] . We used only data found in a lapse of six months. (Details are better explained in Subsection 3). We built time series for these data on purpose to have a correlation matrix in order to find correlation of some kind and in some level of Mexican stock market statistical properties.
Applications on financial engineering have been made of in this article. Just as it was comment at the abstract, we took a database of financial data of Mexican stock market taken from [4] . (Details of database are better explained in Subsection 3.) We built time series for these data on purpose to have a cross correlation matrix that we called “empirical matrix” in order to analyse its eigenvalue spectrum. We plotted these eigenvalue spectrum and we let it ready to compare it with random matrix one as long as we found a random matrix of the same dimension with their respective eigenvalues. Hence we compared both eigenvalue spectrum among them and we pointed out relevant differences and some interesting facts about comparative analysis. Our logic was made in order to consider a null hypothesis and find if expected results from eigenvalue analysis matched; therefore they could confirm our hypothesis. We have to say that our main aim in this work, has been to reproduce the method developed in [3] and emulated in [5] (with some weak points and perhaps another focus and orientation than [3] ). Although, data were different from the one of [5] and the way to proceed was also different. This means (and takes us to the analysis of the data itself). Thereby we can find a bad idea about taking financial data from Mexican stock market to use in a similar procedure as [3] . This is because Mexican stock market does not behave as U.S. does. There are not a lot of factors that matter to this point, but one has to be taken seriously. It is the phenomena related with the continuity of active companies inside the market. On one hand, U.S. market is older than Mexican, so it has been developed and evolved much better and for a long time than Mexican. It is well known that the fluctuation among those recorded in the stock market in U.S. companies is lower than in Mexico companies.
Besides time of functioning, there are several reasons for which U.S. trading market is more stable than Mexican. Mexican stock market is weak because of some political and economic reasons such as the existence of old monopolies in communications industry. These companies have been absorbing small companies so there is no balance at all inside economical finance and trading stock markets. Besides the enormous complexity due to a stock trading system, social and political facts are a motive of a difficult problem to solve in terms of continuity of stock prices. It’s our purpose to analyze and apply a former study done in U.S. to Mexico and understands results in Mexican specific context.
This article is structured as follows: We describe the origin of our financial data, then we fix a cross correlation matrix for these last set of data. Simultaneously to this process, we build random matrix of dimensions equal to cross correlation data. In the next section we show which is the analysis comparing both matrix eigenvalue spectra. We name some applications about risk optimization theory and finally we set up our conclusions in terms of our work done (compared with those from references); hence we set up ideas for future work in this area. One can find whole data information, time series, plots of time series and correlation matrix entries from a special package of [6] .
2. Analyzed Financial Data
2.1. Data Base
We took empirical data from [6] which is a recognized web site in Mexico for financial public reports due to an economy enterprise website, which is not an analysis company but a record company legally certified by Mexican Stock Market. It is not an official page from government neither a private company of financial analysis. But is a new specialized website in economy, finance and generates useful reports for Mexican stock market users. One can find easily other kind of information in this web page referent to other economical systems in the world such as U.S. stock market and Tokio one. The way that registered data of these web site works is the following; they are connected in some way to Mexican stock market web site [4] so they are able to show a lot of financial indicators and their evolution respect to time directly from Mexican stock market. We consider the fact that we cannot depend on data uploaded to web site [6] because of many reasons and we take apart the partition of data for our study and set it up as an independent data base for which we are referring us now on. One can find this separate cluster of data in [7] which belongs to authors web site. One of the main problems in looking out for financial data (and obviously trustful data) is to achieve founding ancient or past financial data from stock markets. This objective becomes tougher if we try to do it with Mexican Stock Market (MSM now on). The problem is not only to find web sites with these data bases but to take them for free or low cost. A lot of this information has been sold for many reasons to private companies in order to be strength while they are trading in MSM. Also furthermore, this information provides not only financial and market information, but economy and political information due to the particularly complicated economic-political system lived in Mexico. This was not the case of [6] . There a lot of places for which financial data on real time can be found but old data are not found that easy. Therefore it was good to find [6] . An example of a screen view reading is offer in Figure 1, and it belongs to [6] .
2.2. Trading Companies
Until this point we have presented where did we take financial data and how do we form financial data base [7] . Now we would like to explain what kind of financial data we took and which are the parameters on time and number of points that we took. We extracted from [6] a 6 months cluster of financial data, from 35 trading companies in this last period and each company has a set of points equal to 130 which represents the evolving variation of Quote and price Index (IPC, by its initials in Spanish). The reason for which we did not take a longer period of trading action was the fact that not all companies trade continuously in MSM because of some reasons yet explained in the last sections. The exact period of time is from December 2013 to May 2014 We may consider that not the whole days of the week are trading days, but only 5 from 7 days. The label of each company is called “ticker” and it is a way to abbreviate each company. Although it is available a lot of information from [6] there is a precise procedure to find out historical data. First step for a user of this online data set is set pointer over the trading company of interest, then apply right click and choose historical information option. Hence it would be possible to see historical and past data set. We used this procedure to set up [6] .
Because [6] is a Mexican financial reviewer, spanish is taken for granted for Figure 1 and Figure 2 and every time that we refer us to [6] . There are further reasons to us for pick these last trading companies. 1) Not all companies enlisted in [6] were taken to [7] (which is our personal data base). At the time of computing our results, there were 140 trading companies approximately. We choose only 130. 2) Those ones chosen were trading companies with continuous regularity on MSM. We can also consider that we were carefully concerned to extract all the companies within IPC. Therefore every trading company taken for [7] is a continuous trading company (at least in time period settled up before), and it has a IPC associated with it. 3) Finally, and by coincidence, [6] in general has registered the dynamics of the most representative trading companies in Mexico. This is easy to understand below the fact that Mexico is, from a political and social point of view, an economic system with a huge amount of monopolies. Hence, almost every trading company found in [6] are deeply strong in market dynamics talked about. A better ordered list of trading companies is shown in Figure 3.
3. Cross Correlation Matrix
We introduce now the construction process to build a cross correlation matrix from financial data empirical measures. From now on we will call C to cross correlation empirical matrix and it is built as follows:
 (1)
(1)
![]()
Figure 2. Information found in [6] for a particular company.
Bracket notation is to point out time average over the period of analysis. The components of this average are gi and gj in the general case we define:
 (2)
(2)
 (3)
(3)
It is clear that dispersion is given by si.
Speaking with economic terms, si is seen as a level of volatility level of a stock market system.
This index is found in financial analysis named “VIMEX” [4] . VIMEX beside INMEX and IPC are the main indexes of financial data an behavior on MSM. We calculated si empirically with financial data from [6] in order to fix computing to a standard method of calculation and a common data base. Although, this index can be found elsewhere.
Construction of cross correlated matrices requires for each entry a quite acceptable description of financial states for each trading company.
We used time series for each company to be represented as entries. As we can see in Figure 1, there are options in [6] (taken also in [7] ) to consult financial state of trading company actions at opening and closure and its behavior with respect to time. This helped us to obtain time series for which will act as components of cross correlation matrix. We now define time series as follows:
 (4)
(4)
and 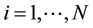 over time period Dt: From now on we will refer to this matrix as C. Besides, the numerical values of the sequence Si belong to the prices or costs of each one of the actions gathered in [7] . Is easy to understand that every stock market price rely on whether the company is probable or not. Time series show us the evolution of these stock prices in time. It is clear from the indexes that time is taken as discrete for this case. Time series values of Cij are only valid for interval [-1,1]. Then Cij = 1 belong to perfect correlation and Cij = -1 belong to perfect anti-correlation. For Cij = 0 case we have no correlation [8] .
over time period Dt: From now on we will refer to this matrix as C. Besides, the numerical values of the sequence Si belong to the prices or costs of each one of the actions gathered in [7] . Is easy to understand that every stock market price rely on whether the company is probable or not. Time series show us the evolution of these stock prices in time. It is clear from the indexes that time is taken as discrete for this case. Time series values of Cij are only valid for interval [-1,1]. Then Cij = 1 belong to perfect correlation and Cij = -1 belong to perfect anti-correlation. For Cij = 0 case we have no correlation [8] .
We now present a necessary constant to compute which is Q = L/N hence, if this number is bigger than one, then C would be positive definite. We need this condition to be held for N ® ¥, y L ®¥ for matrix C, as well as for a random matrix. Computing this constant we have: N = 35 and L = 131, therefore, Q = 3:685714286, which is bigger than one. Because both matrices are positive definite, then, computing C is quite possible. As well as in section 4 for random matrix, positive definite is required. This is in order to satisfy Marcencko-Pastur Theorem conditions [1] , and its results have been helpful.
Time Series
Several kinds of time series have been used for modeling a lot of natural and social phenomena, although, experience in advanced statistics showed that the best approach to stock market behavior is logarithmic time series [3] . For many reasons, this approach is closer than other models to describe mathematically how elements of complex systems evolved in time, besides its correlation. This section is deeply related to trading companies due to the way that we filled this series in terms of trading companies stock prices and its values while evolve in time. Once again, time series values were taken from [6] over a period of six months. We built time series and plot them. One can see in Figure 4 an example of one of all-time series plot for an specific company. Whole set of graphics can be found in [6] .
Computing time series is quite simple. We gather every column of stock prices for each company with software (STATGRAPHICS). Then we set up transformation following logarithmic formula for each value of a single company. Finally we plot this last function with time series form directly of software. All the
![]()
Figure 4. Liverpool time series behavior.
values for this companies once we made transformation are found in [6] . From time series we know that evolution of stock prices can be negative or positive. Also there is useful information that one can take from time series plotting that we cannot find in eigenvalue analysis of correlation matrix. This last and useful information has to do with single behavior of stock prices of each single company. Smoothing process was taken in software analysis; it is helpful because curves can be smoothed such that approach is closer to the limit. One of the main issues about choosing time series periods, is to find which is the better period of time to make measurements. Considering that stock market is open 5 days per week, we pick up measurements from 6 months with stock prices twice a day. We have to keep in mind that IPC index is the one used as stock price indicator. Despite of there are two measurements every day for each company, we took daily average of these values, hence these were used for time series computing. Something really relevant in computing our time series is that [6] give us minimum and maximum values of stock prices for each day and each company, although, taking lnSi(t + Dt) we took maximum as IPC daily return Gi, and opening value as lnSi(t). We computed returns Gi, normalized with average quantities and standard deviations of each stock as well as it was described at the beginning. Once we obtained the gi we generated entries for C. One can find this new data in [7] . Since gi and gj are vectors, we took the whole base in terms of gi and scalar products we made.
4. Random Matrix
Now, we define the random matrices Wigner and Wishart [9] . Let Xtn,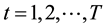 ;
;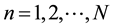 , such that X ~ N (0,1), where Wmn = åXtmXtn, then eigenvalues of W are the elements ln. Hence we used definition above to take advantage of random matrix features and the possibility to relate them to correlation matrices approach. Building random matrix with MATLAB, we generate a random matrix with random entries and with parameters m = 0 and s2 = 1. Taking distribution as before is not only helpful to satisfy definition of random matrix but to follow conditions for Marcencko-Pastur Theorem [10] . From now on we will name random matrix as A. A graphic representation of matrix A is shown in Figure 5. We always remember that order of this matrix is 35 ´ 35.
, such that X ~ N (0,1), where Wmn = åXtmXtn, then eigenvalues of W are the elements ln. Hence we used definition above to take advantage of random matrix features and the possibility to relate them to correlation matrices approach. Building random matrix with MATLAB, we generate a random matrix with random entries and with parameters m = 0 and s2 = 1. Taking distribution as before is not only helpful to satisfy definition of random matrix but to follow conditions for Marcencko-Pastur Theorem [10] . From now on we will name random matrix as A. A graphic representation of matrix A is shown in Figure 5. We always remember that order of this matrix is 35 ´ 35.
5. Spectral Analysis of Both Matrices
We now present the mechanism for which we can compare random matrices eigenvalue bulk versus cross correlation matrices eigenvalue distribution. This is ought to be a representation of Marcencko-Pastur theorem for financial data. It is introduced as follows:

where N ® ¥, T ® ¥ and the quotient satisfies (N/T) ® ¥. Then
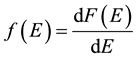 .
.
Therefore
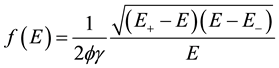
And it holds that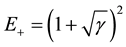 . This interpretation stands for econometrics; it means that there is a relation
. This interpretation stands for econometrics; it means that there is a relation
among eigenvalues of random matrices to correlated matrices.
As one can see (Figure 6), is a canonic density of states such that N/T = 2 is a set of time series of an arbitrary system of a set ready to analyze. Basically, RMT imply that eigenvalue spectrum of a canonic density, such that eigenvalues are probability elements of distribution, and such that they are obtained from financial data of a stock market, can be understood as two sections; one that represents a Marcencko-Pastur behavior and the other one made of eigenvalues for which its eigenvectors have a different direction. One can see in Figure 7 the cut in
![]()
Figure 6. State density of canonic states matrix A.
![]()
Figure 7. Distribution of eigenvalues of C.
x = 1.25, something interesting that has to do with it, is that they intersect curve at an specific point (1.25 for this case) to separate useful information than useless one. It is relevant to point out that density mentioned before presents random correlation, although financial data is normalized, and there are normalized and independent such as building of matrix A and displacement is in other direction. From statistical matrix theory, we know that spectral analysis is the analysis due to eigenvalue and eigenvector distribution as probability distributions [8] . Therefore the main issue to pay attention in this work is to compare both eigenvalue distribution from both matrices (random matrix A and correlated matrix C) with their respective plots. One can see in Figure 7, eigenvalue distribution for C, numerical values and mathematical information of them can be found in [7] . Also, eigenvalue plot for C is shown in Figure 7.
And making a logarithmic approach such as a way to get eigenvalue distribution closer to Marcencko-Pastur requirements we have plot in Figure 8.
Now we can make random matrix eigenvalue analysis for A.
One can have full access to numerical version of distribution in [7] ; they were computed with MATLAB. Although, we obtained plot for this last distribution, and such as we knew from last section, since eigenvectors from A are complex ones, it is hard to handle those numbers to obtain useful information such as Figure 9.
![]()
Figure 8. Eigenvalue distribution of C in logarithmic scale.
Following Marcencko-Pastur Theorem, we see a qualitative similarity from one distribution to another such that make us think in chaotic motion inside MSM because of its isomorphic relation to RMT. Although, study of correlation can lead us to find stability points into this complex system.
6. Conclusion
One of the reasons for which we decided to work with the comparative method between eigenvalue spectrum of RM-Cross correlated matrix, was to reproduce work done in [3] [5] just as we mentioned before. Despite of this kind of orientation, we believe that economy based upon in mathematics and physics has to take another direction of research such as eigenvalue distributions of systems with the clear existence of an approach of RMT to cross correlated matrices. The idea is to understand these distributions and its reciprocal ones in order to analyze integration and punctual statistical properties. Such phenomena can be shown with Wishart matrix and Laguerre distribution.