Random Attractors for Stochastic Reaction-Diffusion Equations with Distribution Derivatives on Unbounded Domains ()
1. Introduction
The understanding of the asymptotic behavior of dynamical system is one of the most important problems of modern mathematical physics; one way to attack the problem for dissipative deterministic dynamical systems is to consider its global attractors. This is an invariant set that attracts all the trajectories of the system. Its geometry can be very complicated and reflects the complexity of the long-time dynamical of the systems. In this paper we investigate the asymptotic behavior of solutions to the following stochastic reaction-diffusion equations with distribution derivatives and additive noise defined in the space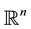 :
:
 (1.1)
(1.1)
with initial data
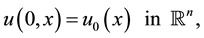 (1.2)
(1.2)
where  is a positive constant;
is a positive constant;  is distribution derivatives;
is distribution derivatives; ; f is a
; f is a
nonlinear function satisfying certain dissipative conditions; hj is given functions defined on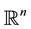 ; and
; and 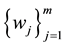 is independent two sided real-valued wiener processes on probability space which will be specified later.
is independent two sided real-valued wiener processes on probability space which will be specified later.
Stochastic differential equations of this type arise from many physical systems when random spatio-temporal forcing is taken into account. In order to capture the essential dynamics of random systems with wide fluctuations, the concept of pullback random attractors was introduced in [1] , being an extension to stochastic systems of the theory of attractors for deterministic equations found in [2] - [5] , for instance. The existence of such random attractors has been studied for stochastic PDE on bounded domains; see, e.g. [6] [7] , and for stochastic PDE on unbounded domains, see, e.g. [8] [9] , and the references therein. In the present paper, we prove the existence of such a random attractor for stochastic reaction-diffusion Equation (1.1) defined in 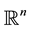 which is not founded.
which is not founded.
Notice that the unboundedness of domain introduces a major difficulty for proving the existence of an attractor because Sobolev embedding theorem is no longer compact and so the asymptotic compactness of solutions cannot be obtained by the standard method. In the case of deterministic equations, this difficulty can be overcome by the energy equation approach, introduced by Ball in [10] and then employed by several authors to prove the asymptotic compactness of deterministic equations in unbounded domains. This idea was developed in [5] to prove asymptotic compactness for the deterministic version of (1.1) on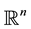 . In this paper, we provide uniform estimates on the far-field values of solutions to circumvent the difficulty caused by the unboundedness of the domains. The main contribution of this paper is to extend the method of using tail estimates of the case stochastic dissipative PDEs and prove the existence of random attractor for the stochastic reaction-diffusion equation with distribution derivatives on the unbounded domain
. In this paper, we provide uniform estimates on the far-field values of solutions to circumvent the difficulty caused by the unboundedness of the domains. The main contribution of this paper is to extend the method of using tail estimates of the case stochastic dissipative PDEs and prove the existence of random attractor for the stochastic reaction-diffusion equation with distribution derivatives on the unbounded domain .
.
The paper is organized as follows. In Section 2, we recall some preliminaries and abstract results on the existence of a pullback random attractor for random dynamical systems. In Section 3, we transform (1.1) into a continuous random dynamical system. Section 4 is devoted to obtain the uniform estimates of solution as . These estimates are necessary for proving the existence of bounded absorbing sets and the asymptotic compactness of the equation. In Section 5, we first establish the asymptotic compactness of the solution operator by giving uniform estimates on the tails of solutions, and then prove the estimates of a random attractor.
. These estimates are necessary for proving the existence of bounded absorbing sets and the asymptotic compactness of the equation. In Section 5, we first establish the asymptotic compactness of the solution operator by giving uniform estimates on the tails of solutions, and then prove the estimates of a random attractor.
We denote by  and
and 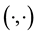 the norm and the inner product in
the norm and the inner product in 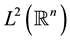 and use
and use 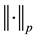 to denote the norm in
to denote the norm in![]() . Otherwise, the norm of a general Banach space X is written as
. Otherwise, the norm of a general Banach space X is written as![]() . The letters C and
. The letters C and ![]() are generic positive constants which may change their values form line to line or even in the same line.
are generic positive constants which may change their values form line to line or even in the same line.
As mentioned in the introduction, our main purpose is to prove the existence of a random attractor. For that matter, first, we will recapitulate basic concepts related to random attractors for stochastic dynamical systems. The reader is referred to [6] [11] -[13] for more details. Let ![]() be a separable Hilbert space with Borel s-algebra B(X), and let
be a separable Hilbert space with Borel s-algebra B(X), and let ![]() be a probability space.
be a probability space.
Definition 2.1. ![]() is called a metric dynamical system if
is called a metric dynamical system if![]() :
: ![]() is
is ![]() - measurable,
- measurable, ![]() is the identity on
is the identity on![]() ,
, ![]() for all
for all ![]() and
and ![]() for all
for all![]() .
.
Definition 2.2. A continuous random dynamical system (RDS) on X over a metric dynamical system ![]() is a mapping
is a mapping
![]()
which is![]() ―measurable and satisfies, for P-a.e.
―measurable and satisfies, for P-a.e.![]() , (1)
, (1) ![]() is the iden- tity on X; (2)
is the iden- tity on X; (2) ![]() for all
for all ![]() (3)
(3) ![]() is continuous for all
is continuous for all![]() . Hereafter, we always assume that
. Hereafter, we always assume that ![]() is a continuous RDS on X over
is a continuous RDS on X over![]() .
.
Definition 2.3. A random bounded set ![]() of X is called tempered with respect to
of X is called tempered with respect to ![]() if for P-a.e
if for P-a.e![]() ,
,
![]()
where![]() .
.
Definition 2.4. Let D be a collection of random subsets of X and![]() . Then
. Then ![]() is
is
called a random absorbing set for ![]() in D if for every
in D if for every ![]() and P-a.e
and P-a.e![]() , there exists
, there exists ![]() such that
such that
![]()
Definition 2.5. Let D be a collection of random subsets of X. Then ![]() is said to be D-pullback asymptotical-
is said to be D-pullback asymptotical-
ly compact in X if for P-a.e![]() ,
, ![]() has a convergent subsequence in X whenever
has a convergent subsequence in X whenever![]() ,
,
and ![]() with
with![]() .
.
Definition 2.6. Let D be a collection of random sunsets of X. Then a random set ![]() of X is called a D-random attractor (or D-pullback attractor) for
of X is called a D-random attractor (or D-pullback attractor) for ![]() if the following conditions are satisfied, for P-a.e.
if the following conditions are satisfied, for P-a.e.![]() , (1)
, (1) ![]() is compact, and
is compact, and ![]() is measurable for every
is measurable for every![]() ; (2)
; (2) ![]() is invariant, that is,
is invariant, that is,
![]()
(3) ![]() attracts every set in D, that is, for every
attracts every set in D, that is, for every![]() ,
,
![]()
where d is the Hausdorff semi-metric given by ![]() for any
for any ![]() and
and![]() . The following existence result for a random attractor for a continuous RDS can be found in [8] [13] . First, recall that a collection D of random subsets is called inclusion closed if whenever
. The following existence result for a random attractor for a continuous RDS can be found in [8] [13] . First, recall that a collection D of random subsets is called inclusion closed if whenever ![]() is an arbitrary random set, and
is an arbitrary random set, and ![]() is in D with
is in D with ![]() for all
for all![]() , then
, then ![]() must belong to D.
must belong to D.
Definition 2.7. Let D be an inclusion-closed collection of random subsets of X and ![]() a continuous RDS on X over
a continuous RDS on X over![]() . Suppose that
. Suppose that ![]() is a closed random absorbing set for
is a closed random absorbing set for ![]() in D and
in D and ![]() is D-pullback asymptotically compact in X. Then
is D-pullback asymptotically compact in X. Then ![]() has a unique D-random attractor
has a unique D-random attractor ![]() which is given by
which is given by
![]()
In this paper, we will take D as the collection of all tempered random subsets of ![]() and prove the stochastic reaction-diffusion equation in
and prove the stochastic reaction-diffusion equation in ![]() has a D-random attractor.
has a D-random attractor.
3. The Reaction-Diffusion Equation on Rn with Distribution Derivatives and Additive Noise
![]() (3.1)
(3.1)
with initial condition
![]() (3.2)
(3.2)
where ![]() is a positive constant,
is a positive constant, ![]() ,
, ![]() , for some
, for some![]() ,
, ![]()
are distribution derivative, ![]() are independent two-side real-valued wiener processes on a probability
are independent two-side real-valued wiener processes on a probability
space which will be specified below, and ![]() with the following assumptions:
with the following assumptions:
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
![]() (3.5)
(3.5)
for ![]() and
and![]() , where
, where![]() ,
, ![]() ,
, ![]() are positive constants and
are positive constants and![]() .
.
In the sequel, we consider the probability space ![]() where
where
![]() .
.
![]() is the Borel s-algebra induced by the compact-open topology of
is the Borel s-algebra induced by the compact-open topology of![]() , and P the corresponding wiener measure on
, and P the corresponding wiener measure on![]() . Then we identify
. Then we identify ![]() with
with
![]()
Define the time shift by
![]()
Then ![]() is a metric dynamical system.
is a metric dynamical system.
We now associate a continuous random dynamical system with the stochastic reaction-diffusion equation over![]() . To this end, we need to convert the stochastic equation with a random additive term in to a deterministic equation with a random parameter. Given
. To this end, we need to convert the stochastic equation with a random additive term in to a deterministic equation with a random parameter. Given ![]() consider the One-dimensional Ornstein- uhlenbeck equation
consider the One-dimensional Ornstein- uhlenbeck equation
![]() (3.6)
(3.6)
The solution of (3.6) is given by
![]()
Note that the random variable ![]() is tempered and
is tempered and ![]() is P-a.e continuous, therefore, it follows form proposition 4.3.3 in [11] that there exists a tempered function
is P-a.e continuous, therefore, it follows form proposition 4.3.3 in [11] that there exists a tempered function ![]() such that
such that
![]() (3.7)
(3.7)
where ![]() satisfies for P-a.e
satisfies for P-a.e ![]()
![]() (3.8)
(3.8)
Then it follows form (3.7), (3.8) that, for P-a.e. ![]()
![]() (3.9)
(3.9)
Putting ![]() by (3.6) we have
by (3.6) we have
![]()
The existence and uniqueness of solutions to the stochastic partial differential Equation (3.1) with initial condition (3.2) which can be obtained by standard Fatou-Galerkin methods. To show that problem (3.1), (3.2) generates a random system, we let ![]() where u is a solution of problem (3.1), (3.2), then
where u is a solution of problem (3.1), (3.2), then ![]() satisfies
satisfies
![]() (3.10)
(3.10)
By a Galerkin method, one can show that if f satisfies (3.3)-(3.5), then in the case of a bounded domain with Dirichlet boundary conditions, for P-a.e.![]() , and for all
, and for all![]() , (3.10) has a unique solution
, (3.10) has a unique solution
![]()
with ![]() for every T > 0, one may take the domain to be a sequence of Balls with radius approaching
for every T > 0, one may take the domain to be a sequence of Balls with radius approaching ![]() to deduce the existence of a weak solution to (3.10) on
to deduce the existence of a weak solution to (3.10) on![]() , further, one may show that
, further, one may show that ![]() is unique and continuous with respect to
is unique and continuous with respect to ![]() in
in ![]() for all
for all![]() . Let
. Let
![]() .
.
Then the process u is the solution of problem (3.1), (3.2), we now define a mapping ![]() by
by
![]() (3.11)
(3.11)
Then ![]() is satisfies conditions (1)-(3) in Definition 2.2 therefore
is satisfies conditions (1)-(3) in Definition 2.2 therefore ![]() is a continuous random dynamical system associated with the stochastic reaction-diffusion equation on
is a continuous random dynamical system associated with the stochastic reaction-diffusion equation on![]() . In the next two sections, we establish uniform estimates for the solutions of problem (3.1), (3.2) and prove the existence of a random attractor for
. In the next two sections, we establish uniform estimates for the solutions of problem (3.1), (3.2) and prove the existence of a random attractor for![]() .
.
4. Uniform Estimates of Solutions
In this section, we drive uniform estimates on the solutions of (3.1), (3.2) defined on ![]() when
when ![]() with the purpose of proving the existence of a bounded random absorbing set and the asymptotic compactness of the random dynamical system associated with the equation. In particular, we will show that the tails of the solutions, i.e. solutions evaluated at large values of
with the purpose of proving the existence of a bounded random absorbing set and the asymptotic compactness of the random dynamical system associated with the equation. In particular, we will show that the tails of the solutions, i.e. solutions evaluated at large values of![]() , are uniformly small when the time is sufficiently large.
, are uniformly small when the time is sufficiently large.
We always assume that D is the collection of all tempered subsets of ![]() with respect to
with respect to ![]() the next lemma shows that
the next lemma shows that ![]() has a random absorbing set in D.
has a random absorbing set in D.
Lemma 4.1. Assume that gj, ![]() , and (3.3)-(3.5) hold. Then there exists
, and (3.3)-(3.5) hold. Then there exists ![]() such that
such that
![]() is a random absorbing set for
is a random absorbing set for ![]() in D, that is, for any
in D, that is, for any ![]() and P-a.e
and P-a.e![]() ,
,
there is ![]() such that
such that
![]()
Proof. We first derive uniform estimates on ![]() from which the uniform estimates on
from which the uniform estimates on![]() . Multipling (3.10) by
. Multipling (3.10) by ![]() and then integrating over
and then integrating over![]() , we have
, we have
![]() (4.1)
(4.1)
For the nonlinear term, by (3.3)-(3.5) we obtain
![]() (4.2)
(4.2)
on the other hand, the next two terms on the right-hand side of (4.1) are bounded by
![]() (4.3)
(4.3)
the last term on the right-hand side of (4.1) is bounded by
![]() (4.4)
(4.4)
where ![]() and
and![]() .
.
Then it follows from (4.1)-(4.4) that
![]() (4.5)
(4.5)
Note that ![]() and
and![]() , therefore, the right-hand side of (4.5) is bounded as following
, therefore, the right-hand side of (4.5) is bounded as following
![]() (4.6)
(4.6)
By (3.9), we find that for P-a.e, ![]()
![]() (4.7)
(4.7)
it follows from (4.5), (4.6) that, all![]() ,
,
![]() (4.8)
(4.8)
which implies that for all![]() ,
,
![]() (4.9)
(4.9)
Let![]() . Applying Gronwall’s lemma, we find that, for all
. Applying Gronwall’s lemma, we find that, for all![]() ,
,
![]() (4.10)
(4.10)
By replacing ![]() by
by![]() , we get from (4.10) and (4.7) that for all
, we get from (4.10) and (4.7) that for all ![]()
![]() (4.11)
(4.11)
Note that![]() .
.
So from (4.11) we get that, for all![]() ,
,
![]() (4.12)
(4.12)
By assumption ![]() is tempered. On the other hand, by definition,
is tempered. On the other hand, by definition, ![]() is also tempered,
is also tempered,
therefore, if![]() . Then there is
. Then there is ![]() such that for all
such that for all ![]()
![]()
which along with (4.12) shows that, for all![]() ,
,
![]() (4.13)
(4.13)
Given ![]()
![]()
Then![]() , further, (4.13) indicates that
, further, (4.13) indicates that ![]() is a random absorbing set for
is a random absorbing set for ![]() in D.
in D.
Which completes the Proof. ,
We next drive uniform estimates for u in ![]() and for u in
and for u in![]() .
.
Lemma 4.2. Assume that ![]() and (3.3)-(3.5) hold, let
and (3.3)-(3.5) hold, let ![]() and
and![]() .
.
Then for every ![]() and P-a.e
and P-a.e![]() , the solutions
, the solutions ![]() of problem (3.1), (3.2) and
of problem (3.1), (3.2) and ![]() of (3.11) with
of (3.11) with ![]() satisfy, for all
satisfy, for all![]() .
.
![]() (4.14)
(4.14)
![]() (4.15)
(4.15)
where C is a positive deterministic constant independent of ![]() and
and ![]() is the tempered function in (3.7).
is the tempered function in (3.7).
Proof. First, replacing t by ![]() and then replacing
and then replacing ![]() by
by ![]() in (4.10) we find that
in (4.10) we find that
![]()
Multiply the above by ![]() and then simplify to get.
and then simplify to get.
![]() (4.16)
(4.16)
By (4.7), the second term on the right-hand side of (4.16) satisfies
![]() (4.17)
(4.17)
From (4.16), (4.17) it follows that
![]() (4.18)
(4.18)
By (4.8) we find that, for ![]()
![]() (4.19)
(4.19)
Dropping the first term on the left-hand side of (4.19) and replacing ![]() by
by![]() , we obtain that, for all
, we obtain that, for all ![]()
![]() (4.20)
(4.20)
By (4.7), the second term on the right-hand side of (4.20) satisfies, for all ![]()
![]() (4.21)
(4.21)
Then, using (4.20) and (4.21), it follows from (4.20) that
![]()
This completes the proof. ,
Lemma 4.3. Assume that gj, ![]() and (3.3)-(3.5) hold, Let
and (3.3)-(3.5) hold, Let ![]() and
and![]() .
.
Then for P-a.e![]() , there exists
, there exists ![]() such that the solutions
such that the solutions ![]() of problem (3.1), (3.2) and
of problem (3.1), (3.2) and ![]() of (3.11) with
of (3.11) with ![]() satisfy, for all
satisfy, for all![]() .
.
![]()
![]()
where C is a positive deterministic constant and ![]() is the tempered function in (3.7).
is the tempered function in (3.7).
Proof. First replacing t by t + 1 and then replacing ![]() by t in (4.14), we find that
by t in (4.14), we find that
![]() (4.22)
(4.22)
Note that ![]() for
for![]() , hence, form (4.22) we have
, hence, form (4.22) we have
![]() (4.23)
(4.23)
Since ![]() and
and ![]() are tempered there is
are tempered there is ![]() such that for all
such that for all ![]()
![]()
which along with (4.23) shows that, for all![]() ,
,
![]() (4.24)
(4.24)
Then from (4.10) using the same steps of last process applying on (4.15), we get that
![]() (4.25)
(4.25)
The above uniform estimates is a special case lemma 4.2, then the lemma follows from (4.24)-(4.25). ,.
Lemma 4.4. Assume that gj, ![]() and (3.3)-(3.5) hold, let
and (3.3)-(3.5) hold, let ![]() and
and![]() .
.
Then for P-a.e![]() , there exists
, there exists ![]() such that the solution
such that the solution ![]() of problem (3.1), (3.2) satisfies, for all
of problem (3.1), (3.2) satisfies, for all![]() .
.
![]()
where C is a positive deterministic constant and ![]() is the tempered function in (3.9).
is the tempered function in (3.9).
Proof. Let ![]() be the positive constant in lemma 4.3, take
be the positive constant in lemma 4.3, take ![]() and
and![]() , by (3.11) we find that
, by (3.11) we find that
![]() (4.26)
(4.26)
By (3.9) we obtain
![]() (4.27)
(4.27)
Now integration (4.26) with respect to s over (t, t + 1), by lemma 4.3 and inequality (4.27), we have
![]() (4.28)
(4.28)
Then the lemma follows from (4.28). ,
Lemma 4.5. Assume that gj, ![]() and (3.3)-(3.5) hold, let
and (3.3)-(3.5) hold, let ![]() and
and![]() . Then for P-a.e
. Then for P-a.e![]() , there exists
, there exists ![]() such that for all
such that for all![]() .
.
![]()
where C is a positive deterministic constant and ![]() is the tempered function in (3.9).
is the tempered function in (3.9).
Proof. Taking the inner product of (3.10) with ![]() in
in![]() , we get that
, we get that
![]() (4.29)
(4.29)
We estimates the first term in the right-hand side of (4.29) by (3.3), (3.4) we have
![]() (4.30)
(4.30)
On the other hand, the second term on the right-hand side of (4.29) is bounded by
![]() (4.31)
(4.31)
The last term on the right-hand side of (4.29) is bounded by
![]() (4.32)
(4.32)
By (4.29)-(4.32) we get that
![]() (4.33)
(4.33)
Let
![]() (4.34)
(4.34)
Since ![]() and
and![]() , there are positive constants
, there are positive constants ![]() and
and ![]() such that
such that
![]()
which along with (3.9) shows that
![]() (4.35)
(4.35)
By (4.33), (4.34) we have
![]() (4.36)
(4.36)
Let ![]() be the positive constant in lemma 4.3 take
be the positive constant in lemma 4.3 take ![]() and
and![]() . Then integrate 4.36 over (s, t + 1) to get that
. Then integrate 4.36 over (s, t + 1) to get that
![]()
Now integrating the above equation with respect to s over (t, t + 1), we find that
![]()
Replacing ![]() by
by ![]() we obtain that
we obtain that
![]() (4.37)
(4.37)
By lemma 4.3 and 4.4, it follows from (4.37) and (4.35) that, for all ![]()
![]() (4.38)
(4.38)
Then by 4.38 and 3.9, we have, for all ![]()
![]()
which completes the proof. ,
Lemma 4.6. Assume that gj, ![]() and (3.3)-(3.5) hold, let
and (3.3)-(3.5) hold, let ![]() and
and![]() .
.
Then for every ![]() and P-a.e
and P-a.e![]() , there exists
, there exists ![]() and
and ![]() such that the solution
such that the solution ![]() of (3.10) with
of (3.10) with ![]() satisfies, for all
satisfies, for all ![]()
![]()
Proof. Choose a smooth function ![]() defined on
defined on ![]() such that
such that ![]() for all
for all ![]() and
and
![]()
Then there exists a constant C such that ![]() for any
for any![]() , multiplying (3.10) by
, multiplying (3.10) by ![]() in
in
![]() , and integrating over
, and integrating over ![]() we find that
we find that
![]() (4.39)
(4.39)
We now estimate the terms in (4.39) as follows, first we have
![]() (4.40)
(4.40)
Note that the second term on the right-hand side of (4.40) is bounded by
![]() (4.41)
(4.41)
By (4.40), (4.41), we find that
![]() (4.42)
(4.42)
From (4.39) the first term on the right-hand side, we have
![]() (4.43)
(4.43)
By (3.3), the first term on the right-hand side of (4.43) is bounded by
![]() (4.44)
(4.44)
By (3.4), the second term on the right-hand side of (4.43) is bounded by
![]() (4.45)
(4.45)
Then it follows from (4.43)-(4.45) we have that
![]() (4.46)
(4.46)
For the second term on the right-hand side of (4.39) we have
![]() (4.47)
(4.47)
For the last term on the right-hand side of (4.39), we have that
![]() (4.48)
(4.48)
Finally, by (4.39), (4.42) and (4.47) (4.48), we have that
![]() (4.49)
(4.49)
Note that (4.49) implies that
![]() (4.50)
(4.50)
By lemma 4.1 and 4.5, there is ![]() such that for all
such that for all![]() ,
,
![]() (4.51)
(4.51)
Now integrating (4.50) over ![]() we get that, for all
we get that, for all ![]()
![]() (4.52)
(4.52)
Replacing ![]() by
by![]() , we obtain from (4.52) that, for all
, we obtain from (4.52) that, for all![]() ,
,
![]() (4.53)
(4.53)
In what follows, we estimate the terms in (4.53). First replacing t by ![]() and then replacing
and then replacing ![]() by
by ![]() in (4.10), we have the following bounds for the first term on the right-hand side of (4.53)
in (4.10), we have the following bounds for the first term on the right-hand side of (4.53)
![]() (4.54)
(4.54)
where we have used (4.7). By (4.54), we find that, given![]() , there is
, there is ![]() such that for all
such that for all ![]()
![]() (4.55)
(4.55)
By lemma 4.2, there is ![]() such that the fourth term on the right-hand side of (4.53) satisfies
such that the fourth term on the right-hand side of (4.53) satisfies
![]()
And hence, there is ![]() such that for all
such that for all ![]() and
and![]() ,
,
![]() (4.56)
(4.56)
First replacing t by s and then replacing ![]() by
by ![]() in (4.10), we find that the third term on the right-hand side of (4.53) satisfies
in (4.10), we find that the third term on the right-hand side of (4.53) satisfies
![]()
This implies that there exist ![]() and
and ![]() such that for all
such that for all ![]() and
and![]() ,
,
![]() (4.57)
(4.57)
Then the second term on the right-hand side of (4.53), there exist ![]() and
and ![]() such that for all
such that for all ![]() and
and ![]() we have that
we have that
![]() (4.58)
(4.58)
Note that![]() ,
,![]() . therefore, there is
. therefore, there is ![]() such that for all
such that for all![]() ,
,
![]()
For the five term on the right-hand side of (4.53), we have
![]()
![]() (4.59)
(4.59)
Note that ![]() and
and ![]() Hence there is
Hence there is ![]() such
such
that for all ![]() and
and![]() .
.
![]() (4.60)
(4.60)
where ![]() is the tempered function in (3.7) and
is the tempered function in (3.7) and ![]() is the positive constant in the last term on the right-hand side of (4.60), By (4.60) and (3.7), (3.8), we have the following bounds for the last term on the right-hand side of (4.53):
is the positive constant in the last term on the right-hand side of (4.60), By (4.60) and (3.7), (3.8), we have the following bounds for the last term on the right-hand side of (4.53):
![]() (4.61)
(4.61)
Let ![]() and
and ![]() then it follows from (4.53), (4.55)-(4.61) that, for all
then it follows from (4.53), (4.55)-(4.61) that, for all ![]() and
and![]() , we have
, we have
![]()
which shows that for all ![]() and
and ![]()
![]()
This completes the proof. ,
Lemma 4.7. Assume that gj, ![]() and (3.3)-(3.5) hold. Let
and (3.3)-(3.5) hold. Let ![]() and
and![]() .
.
Then for every ![]() and P-a.e
and P-a.e![]() , there exists
, there exists ![]() and
and ![]() such that, for all
such that, for all ![]()
![]()
Proof. Let ![]() and
and ![]() be the constant in lemma 4.6 By (4.60) and (3.7) we have, for all
be the constant in lemma 4.6 By (4.60) and (3.7) we have, for all ![]() and
and ![]()
![]() (4.62)
(4.62)
then by (4.62) and lemma 4.6, we get that, for all ![]() and
and ![]()
![]()
which completes the proof. ,
5. Random Attractors
In this section, we prove the existence of a D-random attractor for the random dynamical system ![]() associated with the stochastic reaction-diffusion Equations (3.1), (3.2) on
associated with the stochastic reaction-diffusion Equations (3.1), (3.2) on![]() . It follows from lemma 4.1 that
. It follows from lemma 4.1 that ![]() has a closed random absorbing set in D, which along with the D-pullback asymptotic compactness will imply the existence of a unique D-random attractor. The D-pullback asymptotic compactness of
has a closed random absorbing set in D, which along with the D-pullback asymptotic compactness will imply the existence of a unique D-random attractor. The D-pullback asymptotic compactness of ![]() is given below and will be proved by using the uniform estimates on the tails of solutions.
is given below and will be proved by using the uniform estimates on the tails of solutions.
Lemma 5.1. Assume that gj, ![]() and (3.3)-(3.5) hold. Then the random dynamical system ϕ is D-
and (3.3)-(3.5) hold. Then the random dynamical system ϕ is D-
pullback asymptotically compact in![]() ; that is, for P-a.e
; that is, for P-a.e![]() , the sequence
, the sequence ![]()
has a convergent subsequence in ![]() provided
provided![]() ,
, ![]() and
and ![]()
Proof. Let ![]()
![]() and
and ![]() Then by lemma 4.1 for P-a.e
Then by lemma 4.1 for P-a.e![]() , we have that
, we have that
![]()
Hence, there is ![]() such that, up to a subsequence,
such that, up to a subsequence,
![]() (5.1)
(5.1)
Next, we prove the weak convergence of (5.1) is actually strong convergence. Given![]() , by lemma 4.7, there is
, by lemma 4.7, there is ![]() and
and ![]() such that for all
such that for all![]() ,
,
![]() (5.2)
(5.2)
Since![]() , there is
, there is ![]() such that
such that ![]() for every
for every![]() . Hence, it follows from (5.2) that for all
. Hence, it follows from (5.2) that for all![]() ,
,
![]() (5.3)
(5.3)
On the other hand, by lemma 4.1 and 4.5, there ![]() such that for all
such that for all![]() ,
,
![]() (5.4)
(5.4)
Let ![]() be large enough such that tn ≥ T2 for n ≥ N2. then by (5.4) we have that, for all n ≥ N2,
be large enough such that tn ≥ T2 for n ≥ N2. then by (5.4) we have that, for all n ≥ N2,
![]() (5.5)
(5.5)
Denote by ![]() the set
the set![]() . By the compactness of embedding
. By the compactness of embedding![]() , it fol- lows from (5.5) that, up to a subsequence,
, it fol- lows from (5.5) that, up to a subsequence,
![]()
which shows that for the given![]() , there exists
, there exists ![]() such that for all
such that for all![]() ,
,
![]() (5.6)
(5.6)
Note that![]() . Therefore there exists
. Therefore there exists ![]() such that
such that
![]() (5.7)
(5.7)
let ![]() and
and ![]() By (5.3), (5.6), and (6.7), we find that for all
By (5.3), (5.6), and (6.7), we find that for all![]() ,
,
![]()
which shows that
![]()
as wanted. ,
Now we are in a position to present our main result: the existence of a D-random attractor for ![]() in
in ![]()
Theorem 5.2. Assume that![]() ,
, ![]() and (3.3)-(3.5) hold. Then the random dynamical system
and (3.3)-(3.5) hold. Then the random dynamical system ![]() has a unique D-random attractor in
has a unique D-random attractor in![]() .
.
Proof. Notice that ![]() has a closed random absorbing set
has a closed random absorbing set ![]() in D by lemma 4.1, and is D-pullback
in D by lemma 4.1, and is D-pullback
asymptotically compact in ![]() by lemma 5.1. Hence the existence of a unique D-random attractor for
by lemma 5.1. Hence the existence of a unique D-random attractor for ![]() follows from proposition 2.7 immediately. ,
follows from proposition 2.7 immediately. ,
Foundation Term
This work was supported by the NSFC (11101334).
NOTES
*Corresponding author.