Using Manipulatives in Solving and Posing Mathematical Problems ()
1. Introduction
The National Council of Teacher of Mathematics’ [NCTM] Principles and Standards promotes the use of multiple representations (e.g., pictorial, manipulatives, graphical, numerical) in mathematics classroom to assist students in exploring mathematical concepts ( NCTM, 2000 ). This use could be one potential way to introduce abstract mathematical ideas for younger students ( Shulman, 1986 ). Meanwhile, Cramer, Post, & del Mas (2002) believed that the representational models teachers utilized in classrooms could engage and facilitate students’ learning and knowledge construction. Teachers’ roles are to help students make connections among various representations in mathematics.
Among representations, the use of manipulatives has been invaluable in teaching and learning in school mathematics ( Clements, 1999 ; Karshmer & Farsi, 2008 ). In fact, many prekindergarten through middle grade classroom teachers use concrete models and virtual manipulatives as teaching tools to help students learn concepts in number and operations, geometry, algebra, measurement, and data analysis and probability. Therefore, the purpose of this paper is to explore the use of manipulatives in school mathematics for developing students’ understanding of problem solving and problem posing. This manuscript includes theoretical underpinnings underling the use of manipulatives and then discusses its roles in school mathematics. Next it focuses on the advantages of using manipulatives in problem solving and problem posing and ways to improve the usage followed by concluding remarks.
2. Theoretical Underpinnings
Because teaching and learning mathematics is an arduous practice ( Moss & Case, 1999 ), NCTM (2000) has stated that teachers should comprehend the mathematics they are teaching and choose appropriate instructional materials to present content for students efficiently and effectively. Additionally, teachers need to evaluate what kinds of representations are best for presenting certain mathematical ideas to increase student learning ( Shulman, 1986 ). Seeing that teachers play a significant role during classroom instruction, teachers must understand how students learn ( Even & Tirosh, 2002 ). For younger children, active learning in preschool and elementary school is crucial because this stage is the most critical period for brain development ( Hatfield, Edwards, Bitter, & Morrow, 2003 ).
Based on John Dewey’s (1938/1997) experiential learning theory, concrete experience is the source of learning and cognitive development because individuals learn by doing. Similarly Piaget (1964) believed younger children were active learners of knowledge through assimilation and accommodation processes. Children continually construct their own knowledge across four cognitive developmental stages: sensorimotor (toddler to two years old), preoperational (two to six year old), concrete operational (six to twelve years old), and formal operational (over twelve years old). Piaget argued that when students at pre K and elementary school formally learn mathematics, they learn concepts better through the use of hands-on materials that help them build mental sense and structure of abstract ideas. Over time, students construct and restructure their knowledge through teachers’ facilitation and social interaction ( von Glasersfeld, 1989 ; Vygotsky, 1978/2009 ). As they enter the formal operational stage, Piaget claimed that the majority of students can build their mental transformation wherein they are capable of seeing the abstract concepts without concrete materials.
Along these same lines, Bruner (1973) and Montessori (1914/1964) contributed their scholarly ideas on cognitive development specifically about how children represent their understanding. Through Bruner’s stages of representation, children interact throughout the learning process across three modes of representing reality: enactive, iconic, and symbolic. According to Bruner, enactive is the learning stage where children heavily depend on physical objects. Iconic refers to utilizing pictorial and graphic representations whereas symbolic is the ability to use words and symbols for learning to occur. When adapting this theory within the practice of learning mathematics, it has been suggested that teachers first use objects such as base-10 blocks, Cuisenaire rods, and cubes as medium for helping younger students discover and construct their knowledge in concrete ways ( Hatfield et al., 2003 ). Then slowly, teachers can facilitate students’ progress to pictorial and symbolic. On the other hand, Montessori focused on children’s self-directed learning through five multi-sensory approaches. Her curriculum materials included engaging and enjoyable hands-on activities to help children internalize concepts and make ideas easier to comprehend.
The significant works from these prominent scholars have appealed to and advocated for today’s mathematics classroom movement toward a constructivist way of teaching and learning. These theoretical underpinnings are the foundation for the use of manipulatives in mathematics classroom but not limited for primary school students.
3. Solving Problems with Manipulatives
In helping young children construct their own mathematical knowledge, many teachers consider a hands-on approach that involves the use of manipulative materials as teaching aids in classrooms ( Burns, 2007 ; Moyer, 2001 ; Swan & Marshall, 2010 ). Manipulatives are “objects designed to represent explicitly and concretely mathematical ideas that are abstract” ( Moyer, 2001: p. 176 ). Manipulatives represent an external reality of abstract ideas that promote reflective thinking ( Van de Walle, Karp, & Bay-Williams, 2009 ). Teachers use manipulatives to support students’ conceptual acquisition of abstract symbols and mathematical language. According to Fuson, Kalchman, & Bransford (2005) , conceptual understanding refers to the ability to comprehend mathematical concepts, operations, and relations. Classroom instruction should focus on the construction of knowledge and underlying structure in meaningful ways for developing students’ conceptual understanding ( Eisenhart, Borko, Underhill, Brown, Jones, & Agard, 1993 ). Meanwhile, rules and procedures should not be the main agenda when teaching and learning mathematics until students have understood concepts profoundly ( Burns, 2007 ). In fact, Van de Walle et al. (2009) strongly believed that “rules should never be taught or used until the students understand what the result means” (p. 308). With this information in hand, students must understand intuitively how and why mathematical operations produce certain correct answers without solely memorizing algorithms ( Moyer, 2001 ).
In addition, many researchers ( Clements, 1999 ; Moyer, 2001 ; Swan & Marshall, 2010 ) argued that these manipulatives themselves do not convey the meaning of mathematical concepts. In fact, students must be able to reflect on their actions and explore the concepts themselves; therefore, it is very important for teachers to help students “see” the mathematical relationships between the materials and abstract symbols ( Van de Walle et al., 2009 ). For example, a concrete manipulative such as paper folding (Figure 1) can be used for teaching and learning equivalent fractions. Students should be able to construct their knowledge of unit wholes and part of whole concepts when folding a piece of paper. As students fold the paper into two parts, shade a part of it, they
should be able to recognize the relationship, the shaded part is 
of one unit whole. The concept is the rela-
tionship between the models as students fold the papers. Once students fold the paper vertically for the second time, they should see that the paper is now partitioned into four parts and the same shaded area is equivalent to
. As the folding process continues, teachers can facilitate students’ knowledge construction of equivalent fractions,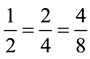
. Students must be aware that the idea of 
is the relationship among the models that
students have to construct in their minds; the models help students see the relationships between paper folding and equivalent fractions.
In classrooms, teachers use manipulatives to introduce abstract mathematical concepts and extend younger students’ prior knowledge ( Hunt, Nipper, & Nash, 2011 ; McNeil & Jarvin, 2007 ). Utilizing concrete objects that relate to students’ context can help them develop their problem solving and problem posing skills. As an example, Empson (2002) presented a task to children in her classroom “4 children are sharing 10 brownies so that everyone gets the same amount. How much brownie can 1 person have?” (p. 29). In this scenario, 10 brownies
can be shared among four children by using the partitive concept, as a result each student can have 
brownies; teachers can show students how the distribution process of whole numbers would result in fractional numbers ( Behr, Lesh, Post, & Silver, 1983 ). In this problem solving task, teachers can help students construct their basic fractional knowledge while distributing the items equally focusing on the idea of sharing ( Van de Walle et al., 2009 ). Students are engaged in problem solving as they manipulate real-life objects as they search for a solution ( Kelly, 2006 ). According to Kelly, teachers can assess students’ learning in relation to the use of manipulatives in problem solving through rubric-style assessments as measures of what was taught and practiced.
Manipulatives have been useful as teaching aids for students with learning disabilities ( Cass, Cates, Smith, & Jackson, 2003 ; Marsh & Cooke, 1996 ). In one study, Marsh and Cooke investigated the use of manipulatives in teaching and learning mathematical problem solving with three learning-disabled students who were first given verbal instructions for solving word problems and later introduced to Cuisenaire rods for setting up word problems for computation. Results showed students were able to identify the correct operation needed when solving the problems using manipulatives. Additionally, they were able to make generalizations to written problems
![]()
Figure 1. Paper folding model for equivalent fractions.
without using manipulatives as a result of the instruction using rods. However, these researchers noted some limitations that might have contributed to the effect of this instruction because positive effects were difficult to be generalized to different settings when students were assessed directly after each manipulative session.
The use of manipulatives provides concrete experiences that helped students engage actively in knowledge acquisition ( Clements, 1999 ). According to DeGeorge & Santoro (2004) , students can visualize mathematics concepts when using rods, cubes, and other concrete models in absence of real-life objects. In fact, NCTM (2000) states that “Concrete models can help students represent numbers and develop number sense; they can also help bring meaning to students’ use of written symbols and can be useful in building place value concepts” (p. 80). Teachers need to nurture students in using models effectively as tools for knowledge construction of number sense because these concepts are important for subsequent learning in mathematics ( Barnett-Clarke, Fisher, Marks, & Ross, 2010 ).
4. Utilizing Manipulatives When Posing Problems
According to Cramer and Henry (2002) , manipulatives allow students to construct mental images of fractions that enable them to understand concepts. In problem posing, teachers can enhance students’ understanding of division of fraction using models such as fraction circles and strips, paper folding, and chips. Thus when stu-
dents are asked to pose a scenario problem for this equation, 
( Sowder, Philipp, Armstrong, &
Schappelle, 1998 ), they can use fraction strips to discover fraction size ( Cramer & Henry, 2002 ) and the relationships between the fourth and the eighth. Teachers can probe students’ thinking by asking them to explain the
meaning of
. Students should be able to reflect on their thinking when comparing fourths and eighths side
by side as illustrated in Figure 2. From this figure, students should be able to recognize the relationship between models and make connections to their prior knowledge about fractional numbers. Teachers can facilitate students’ learning throughout the process of manipulating models. Students are supposed to be able to internalize
ideas and notice the underlying relationship, six sets of 
in
. Based on this understanding, students might
be able to think of a scenario that fits the model and then teachers can ask them to share their scenarios with other classmates. Let us consider the following posed scenarios.
Student A: Mary made 
pounds of salad mix. If she puts 
of a pound of the salad mix into a container, how many containers can Mary fill?
Student B: Sally had 
of a pie left, her 8 friends came over and wanted a piece. She had to divide the left over pie into 8 equal parts. How big was each part?
![]()
Figure 2. Models for division of fraction.
The analysis showed that student A might have had a better understanding of the idea of fair sharing because she or he was able to pose a realistic scenario that fit into the models shown in Figure 2. This student could differentiate between “how much?” versus “how many?”. According to Sowder et al. (1998) , it was important to capture students’ understanding of two kinds of questions that looked at similar but different mathematical concepts related to proportional reasoning.
In comparison, student B failed to notice the scenario problem he or she provided was incorrect. Based on an error-analysis, the student misunderstood the concepts of division by one eighth with division by eight, leading to a common error in posing a scenario problem ( Suzuka et al., 2009 ). In addition, student B did not realize the
division computation for her or his scenario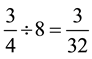 
was different from the one that was presented and worked on previously,
. Nevertheless, as a remedial instructional strategy, teachers could ask student B to
solve their posed scenarios and then determine how the student derived the answer. Then, teachers can communicate the relationships between models to students and provide necessary feedback so that students in the class can restructure their understanding. Finally, after students have mastered the idea conceptually, teachers can
show the procedural process of the invert and multiply rule,![]()
. In relation to learning ra-
tional numbers, Van de Walle et al. (2009) argued that teachers should not introduce the concept based on rules and algorithms (e.g., invert and multiply) even though these strategies seemed efficient and easy to operate. This process of teaching and learning is an enduring process; as students continue reflecting on their thinking they are constructing and restructuring the concepts.
5. Improving the Use of Manipulatives
In previous examples of problem solving and problem posing, manipulatives have helped students see the relationship of mathematical concepts and build their own knowledge gradually. In addition, the use of manipulatives has the potential of boosting their abilities to solve and pose scenario problems related to their real-life ( Rosli et al., 2015 ). After all, there still seems to be much room for improvement with the use of manipulatives in the information age era ( Clements, 1999 ). Despite the benefits of using manipulatives, there has been a continued debate over its drawbacks. Based on their review of scholarly works, McNeil and Jarvin (2007) claimed manipulatives have little impact on students’ learning and suggested teachers reduce the use of certain models that can hinder the learning of mathematics. In addition, Van de Walle et al. (2009) countered teachers who misused manipulative materials when presenting a particular mathematical concept; consequently students might blindly learn to use them in a rote manner with little or no understanding of the concept ( Uttal, O’Doherty, Newland, Hand, & Deloache, 2009 ). Therefore, the effective use of manipulatives is important because these tools could possibly harm student learning during mathematics instruction ( Puchner, Taylor, O’Donnell, & Fick, 2008 ; Moyer, 2001 ). In fact, Van de Walle et al. (2009) stated “A mindless procedure with a good manipulative is still just a mindless procedure” (p. 34).
In the present technologically-savvy world, virtual manipulatives have been increasingly used in addition to concrete objects. Clements (1999) , Hunt, Nipper, & Nash (2011) , Moyer-Packenham, & Westenskow (2011, 2013) , Zuckman, Arida, & Resnick (2005) argued that virtual manipulatives were meaningful and efficient because they are more manageable, clean, dynamic, interactive, and extensible. They can create new forms of representation for mathematics instruction and link iconic and symbolic notations ( Hunt, Nipper, & Nash, 2011 ). Additionally, Moyer, Bolyard, & Spikell (2002) believed that teachers and students are more able in accessing virtual manipulative resources on the World Wide Web anywhere and anytime. As an example, as the world’s largest mathematics organization, NCTM has designed Illuminations that provide comprehensive recourses and materials which are aligned with the Principles and Standards for School Mathematics ( NCTM, 2000 ). The Illuminations website offers online activities according to grade levels and content standards for helping teachers in improving teaching and learning mathematics. In addition, there are collections of virtual manipulatives available that teachers and students can use to enhance learning such as the National Library of Virtual Manipulatives (2010) , Shodor Interactivate Activities (2011) , and MSTE at the University of Illinois (2011) . These resources are useful for teachers, so they can organize their classroom instruction effectively with activities that engage students to learn mathematics.
Many research studies have found positive impacts of using virtual manipulatives for teaching and learning mathematics (e.g., Moyer-Packenham, Salkind, & Bolyard, 2008 ; Steen, Brooks, & Lyon, 2006 ; Suh, Moyer, & Heo, 2005 ). For instance, Suh et al. designed an experiment that utilized virtual manipulative fraction concept tutorials for three fifth-grade mathematics classroom in learning of equivalence and fraction addition. This study demonstrated that low achieving students seemed to benefit the most out of the three groups (low, average, high achieving students) by working with the virtual concept tutorial. The results provided ways which could facilitate the connection between conceptual and procedural understanding based on the graphic and non-linguistic features of virtual fraction manipulatives. However, as teaching tools, virtual manipulatives can either be used effectively or not at all depending on how teachers use them in classrooms.
As a way to improve the teaching and learning of mathematics, it is important for teachers to set appropriate standards for the effective use of manipulatives in classrooms ( Kelly, 2006 ). First, manipulatives should not be referred to as toys causing students to think of them as something with which to play ( Clements, 1999 ; Kelly, 2006 ; McNeil & Jarvin, 2007 ). Second, teachers must be capable of utilizing manipulatives in a detailed-format efficiently in a way to encourage student learning constructively to diminish misconceptions ( Kelly, 2006 ; Uttal et al., 2009 ). Third, teachers should model and use manipulatives directly in order to help students see relationships and be able to make the connection to abstract symbols and mathematical language ( Clements, 1999 ; Uttal et al., 2009 ). Lastly, manipulatives should be included consistently as part of discovery learning ( Bruner, 1973 ) that builds students’ skills as problem solvers and problem posers.
6. Conclusion
In summary, teaching and learning mathematics for conceptual understanding is a challenging and complex process. The effective use of manipulatives as teaching tools has the potential to enhance students’ mathematical learning. A large body of literature has shown the advantages of using manipulatives but there was also been research reported on their disadvantages. As teachers are the agents of change, they should know when, why, and how to use manipulatives efficiently and effectively ( Kelly, 2006 ). It is hoped that manipulatives will be an important part of mathematics instruction in helping students to build conceptual understanding of abstract topics. The education research community must continually contribute ideas and ways for improving manipulative use by focusing on research both inside and outside of classrooms.