1. Introduction
In Economics, when working with time series we understand that they are the result of an unknown generating process, and alternative methods to ascertain the properties of the underlying dynamics are necessary. This is particularly relevant when it comes to analyzing the possible interrelation between two (or more) variables, which is a primary research topic in Economics. Different procedures have been proposed in the literature to test the interrelations or statistical dependencies among time series: these include the widely used Pearson, Spearman, and Kendall correlation coefficients, Hoeffding D-measure, methods based on mutual information, and a good number of more recent contributions: distance correlation [1] , the maximal information coefficient [2] , the Heller-Heller-Gorfine measure [3] , Copula-based methods1, and more.
The best known is the Pearson correlation coefficient, which is also simple to obtain and interpret. Nevertheless, this tool only serves to detect linear dependencies. The Spearman and the
Kendall
rank correlation coefficients work well in identifying linear and monotonic nonlinear relationships, but they are less than adequate in detecting other kinds of nonlinearities. Besides, if the data set is large, assigning ranks to long series is costly in calculation terms, and using rank correlation measures is problematic when the series have a large number of repeated values (which is common with the value zero in many financial series). In this case, the results being obtained can be deceptive. The other methods being mentioned are valid, in principle, for the detection of all types of relationships, although some are also computationally complex and others, like those based on Copula functions, are also difficult to implement. All these approaches are valid only in asymptotic terms, since the exact probability distributions of the corresponding test statistics are unknown. A comparative study of some of these methods is found in [5] .
In this work, we propose a method to test for the existence of statistical dependence (linear or nonlinear) between two time series whose data-generating processes are unknown. We wish to emphasize that, as we will show later, our test procedure presents two advantages: its simplicity of implementation and interpretation, and its basis in an exact probability distribution.
Our starting point is the methodology based on the so-called Recurrence Plots, RP, (Eckmann et al. 1987) [6] , and more specifically on the Recurrence Quantification Analysis, RQA, (Zbilut and Webber, 1992 [7] and Webber and Zbilut 1994 [8] ). Both RP and RQA have been used to analyze the properties of dynamical systems in Physics, Chemistry, Biology, and, more recently, in Economics. Some references from the field of Economics are [9] - [18] . A review of the applications of this technique to different fields can be found in [19] , where its increasing use in Economics is noted, particularly in the study of Financial Markets.
The analysis of the recurrences provides very useful information, as much about the structure of the underlying systems as about the possible links or interrelations among them. This last is studied through the multivariate extensions of the RQA: the so-called “cross recurrences” and “joint recurrences”. Our test procedure is specifically based on these latter.
The rest of the paper is structured as follows. In Section 2, we give a brief explanation of the methodology used. In Section 3, we choose a measure of the joint recurrences and obtain its probability distribution under the hypothesis of independence. In Section 4, a statistical test using this distribution is defined. Sections 5 and 6 deal with the application of the proposed method to simulated and economic series respectively. Finally, Section 7 provides a summary of our main conclusions.
2. The Recurrence Plot and the Recurrence Quantification Analysis
As we have indicated in the previous section, the starting point of this work is the so-called Recurrence Plot, a graphic tool that displays the recurrences of a data series (x), constructed using the Recurrence Matrix, RM:
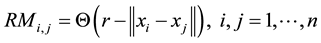 , (1)
, (1)
where Q is the Heaviside function, r is a predefined distance threshold (or “radius”), and xi, xj are observations, or system states. Clearly, the Recurrence Matrix, RM, is a symmetric n ´ n matrix2, with the values “ 1” of this matrix being the RP points. The aim of this tool is to detect patterns of recurrence in the data, one of the most important characteristics of dynamical systems.
In order to improve the quality of the information provided by the RPs, Zbilut and Webber (1992) [7] and Webber and Zbilut (1994) [8] quantify the information underlying the RP by means of a series of indicators based on the point density and on the structures that form certain lines in the plot. This methodology is called “Recurrence Quantification Analysis” (RQA). More recently, two extensions of this same methodology have been proposed to analyze the relationship between different systems. The first of these is the Cross Recurrence Plot (CRP), designed by Zbilut et al. (1998) [21] to analyze dependencies between two systems by comparing their states. To do this, the Cross Recurrence Matrix (CRM) is used, defined as:
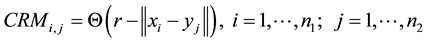 , (2)
, (2)
where xi are the observations from the first system and yj are the observations from the second system. The CRP is obtained from this matrix and shows the recurrences of each of the states of one of the systems with each of the states of the other.
The second extension is the Joint Recurrence Plot (JRP), proposed by Romano (2004) [22] to analyze the interrelation between two systems. The starting point in this case is the individual recurrences of the observations of each system, from which the Joint Recurrence Matrix (JRM) is constructed, defined as:
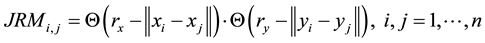 (3)
(3)
The JRM is a symmetric matrix, since both RMs are symmetric. The values “ 1” of this matrix correspond to the simultaneous recurrences of both systems, hence being the points of the JRP. So, if both systems are related in some way, they must present a high number of joint recurrences. On the contrary, if they are not, or if the relationship is very weak, the number of joint recurrences should be small.
Marwan et al. (2007) [23] study and compare the CRP and the JRP, concluding that “CRPs are more appropriate to investigating relationships between the parts of the same system… On the other hand, JRPs are more appropriate for the investigation of two interacting systems that influence each other”.
Our main goal in this article is to obtain a criterion that enables us to distinguish whether two dynamical systems are independent or not. To do this, we use a measure obtained from the joint recurrences, the “Joint Percentage of Recurrence” or “Joint Recurrence Rate”, JREC, which summarizes the most relevant information of the JRP.
This same approach is adopted in two recent works, [24] and [25] , in which the joint recurrences are used to test interrelations and connectivity between real series. The authors introduce an indicator that they denominate “Recurrence-Based Measure of Dependence”, from which they construct a simple statistical test to determine whether both series are (or are not) connected. This statistical test is carried out using surrogate data sets, so its probability distribution is not exact, having only asymptotic validity. Our test procedure is based on the same methodology, it is equally easy to apply and interpret, and it is based on an exact probability distribution, which implies that it can be used for data series of any length.
3. The JREC Statistic and Its Probability Distribution
As mentioned above, the JRP shows the joint recurrences of two series, x and y. Given that its construction requires that both recurrence matrices have the same order, the series that we will use to build the JRP must be of equal size, n. Since individual recurrence matrices are symmetric and all points on their main diagonal are trivially recurrent, the same will occur with the JRM matrix. Thus, from now on, only the upper (or lower) triangular part of these matrices, excluding the main diagonal, will be used. In the rest of the paper, when we refer to RM and JRM, it should be understood that we are dealing with their corresponding triangular parts.
The main indicator that summarizes the information contained in the JRP is the JREC, defined as JREC = 100 (NJR/NP), where NJR is the number of recurrence points of the JRP, or number of 1s of the JRM, and NP is the total of the elements of the JRM. Obviously, NP = n(n − 1)/2.
We denote by NRx and NRy the number of recurrence points of each series (x and y), and RECx and RECy their corresponding recurrence rates. Hereafter, if individual recurrence ratios are different, subindex 1 will be assigned to the RP with the smaller recurrence, and subindex 2 to the RP with the larger recurrence. It is then evident that 0 £ JREC £ REC1 £ REC2.
The greater the JREC value, the larger the percentage of simultaneous recurrences. Consequently, in general terms, if both series have been generated from systems with a high degree of dynamical similarity, the JREC value will be close to the maximum (REC1)3. By contrast, if both series have been generated from independent systems, the JREC value would be small. Although in principle one could think that, in this case, JREC should be equal to zero, this is not necessarily true. Even in series coming from completely independent systems, joint recurrences can appear by chance.
However, in practice, we do not have a proximity criterion. Additionally, for intermediate values, this indicator would not lead us to conclusive results. Consequently, a statistical test providing a cut-off point that allows us to establish whether both series are independent or not, would be necessary.
In order to construct this test, we will obtain the probability distribution of the random variable NJR for a JRP built from two series generated in independent processes (for example, two purely random series), which will give a structure and a number of points of the JRP that are absolutely random. This assumption of independence will be the null hypothesis of the test.
Under the null, the probability that a point of the first recurrence plot, RP1, is also a point of the second one, RP2, is NR2/NP. And, obviously, the probability that a point of the RP1 is not a point of the RP2 is (NP-NR2)/NP. Consequently, the probability that no point of the RP1 is a point of the RP2, and hence P(NJR = 0), is given by the expression:
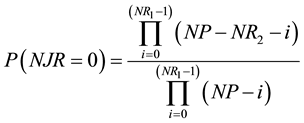 (4)
(4)
The probability that only one point of the RP1 is also a point of the RP2, i.e. P(NJR = 1), is given by the product of three terms:

The first term is the probability that a point of the RP1 is also a point of the RP2. The second term is the probability that the remaining points of the RP1 are not points of the RP2. The result is multiplied by NR1, the number of different cases that can appear. After rearranging, we obtain:
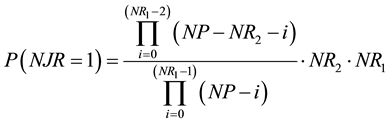
Reasoning in a similar way, the probability that there are two points in the JRP would be:

The first term is the probability that two points of the RP1 are also points of the RP2. The second term is the probability that the remaining points of the RP1 are not points of the RP2. The third term is the number of possible different combinations of pairs of recurrent points of the RP1. Rearranging terms, we obtain:
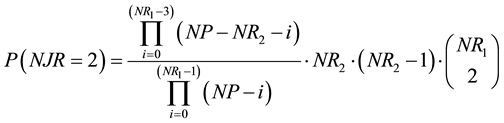
In general terms for NJR = k (0 < k < NR1) we would obtain the following expression:
 , (5)
, (5)
for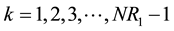 .
.
Finally, for NJR = NR1 the resulting probability would be:
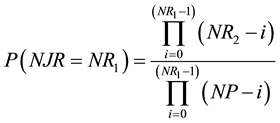 . (6)
. (6)
This probability distribution is the key tool that will enable us to test whether, in a JRP obtained from two real series, the number of points differs significantly from the expected if both series had been generated from independent processes (the null hypothesis of our test). Hence, rejecting the null hypothesis would be evidence, for the chosen significance level, that both series are related, presenting a certain degree of statistical dependence or dynamical similarity.
4. Testing Procedure
Our test procedure is based on a comparison of the JREC value of the chosen series with the expected value of the JREC, E(JREC), of two series generated from independent systems. E(JREC) can be trivially obtained from E(NJR), i.e. the mathematical expectation of the probability distribution derived in the previous section. Note that, even under independence, points in the JRP may appear (“false non-independences”). In general terms, the number of these false non-independences will be greater, the greater the number of recurrence points in the individual RPs. Hence, the existence of a high number of points in the JRP does not necessarily mean statistical dependence. This would only be accepted if the number of points of the JRP is significantly greater than the number we would expect if both series were independent. In this case, we would conclude that there is evidence to reject the null hypothesis, that is to say, to accept that there exists a relationship (of some kind) between the series.
In order to apply our test procedure, the following five steps must be performed:
1) Select the two-series object of study, which can be simulated or real. In previous analyses, we have verified that the existence of trend (deterministic or stochastic) in the series may give rise to trivial recurrences. To avoid these “spurious” recurrences the real series should be detrended.
2) Construct the RPs of both series. In order to do this, it is necessary to set the value of the radius r. This radius is a threshold, or distance, that determines the criterion of proximity. Schinkel et al. (2008) [20] state that, “for JRPs the threshold should be chosen in a fashion that the recurrence point density is the same in the individual RPs”. As in our previous work ( [14] , [15] and [16] ), we choose a value of r to achieve a portion of recurrence points equal to 10%. Thus, in all cases, REC1 = REC2 = 104.
3) Construct the JRP and compute the number of recurrence points, NJR.
4) Obtain the probability distribution of NJR, using expressions (4), (5) and (6). As it has already been demonstrated, the only required data are NP, NR1 and NR2.
5) Calculate the p-value of the test, i.e. the lowest significance level for which the null hypothesis should be rejected.
To illustrate the procedure described above, we will apply it initially to the two following cases:
First, the series x and y obtained from a simulation of the Henon chaotic system5; as both were generated in the same system, we expect the result of our test to show a clear relationship.
Second, two series obtained respectively from the Henon and the Ikeda chaotic systems; these series come from two different systems, so the results of the test should reflect their independence.
The results obtained, for n = 200, 500, and 1000, are shown in the following table.
![]()
Table 1. Results of the application of the test to two pairs of simulated series.
Table 1 shows:
・ The number of points (NJR), and the percentage of recurrence (JREC) of the JRP;
・ The expected average values of NJR and JREC if both systems were independent, E(NJR) and E(JREC);
・ The p-values associated with each of the tests.
The results obtained are conclusive:
For the two series generated from the Henon system, the NJR and JREC values are approximately four times greater than would have been expected if both series were independent. The p-values are equal to zero, so that the null hypothesis is clearly rejected. This occurs in all three sample sizes. For the series generated from different systems, Henon and Ikeda, the values of the indicators are very close to those expected under the null hypothesis. The large p-values obtained in this case provide no evidence against the null hypothesis for the three sample sizes, at any level of significance.
These results can be considered an illustration of the good behavior of the test procedure in two extreme cases. Next, in order to better study its performance, we will use the same systems transformed in the following way:
First, we apply the test procedure to the series x and y of the Henon system, affected in this case with different levels of additive noise (as a percentage of the standard deviation of the series). As is obvious, noise distorts the structure of the system, so the higher the level of noise, the weaker should be the relationship between the series. This would have to be reflected in the results of our test.
Second, we apply the test procedure to the unidirectionally coupled Henon and Ikeda systems. Specifically, we consider the Ikeda system to be driven by the Henon system, with different levels of coupling. Each value of the coupling strength parameter reflects the amount of coupling between the systems. Our test should reflect the fact that the greater the value of this strength parameter, the greater will be the NJR and JREC values, and thus the greater the interdependence between both systems.
The results obtained, with a sample size n = 500 are shown in Table 2:
The results displayed in Table 2 show that, in the case of the Henon system, if the noise level increases, the joint recurrences decrease. As could be expected, the interdependence between both series is maintained for small levels of noise, and diminishes as the noise level increases, until it is completely lost when the series are strongly distorted by noise. This last happens for a level of noise close to 80%.
For the Henon - Ikeda coupled system, the results also agree with what we could expect: if the strength parameter increases, so does the interdependence between both systems. For small values of the strength parameter, both systems behave as independent (the null hypothesis could not be rejected). This is the situation until this parameter reaches a value of about 0.1, when we fail to reject the null hypothesis at a significance level of 0.05. From this parameter value onwards, the level of dependence between the systems increases continuously, reaching, for greater values of the parameter, p-values equal to zero. In these cases, when the null hypothesis cannot be rejected at any level of significance, we can state that our test concludes that both systems are totally coupled.
Obviously, only a few systems and one simulation in each instance are not sufficient to evaluate the adequacy of the testing procedure. Thus, more systems and a greater number of replicas should be used. This will be done in the next section.
5. Application of the Test Procedure to Simulated Series
In order to analyze the reliability of the proposed method, the previous examples should be extended in two ways:
![]()
Table 2. Results of the application of the test to the series of the Henon system affected by noise, and to a pair of series of the Henon - Ikeda coupled system [E(NJR) = 1247, E(JREC) = 1].
1) Use a wide set of systems that permit more situations of both interrelation and independence to be covered;
2) Repeat each experiment many times.
In this section, the test procedure is applied to simulated series from the following systems:
・ Two chaotic deterministic systems (Henon and Ikeda);
・ One non-chaotic deterministic system with strange attractor (Gopy)6;
・ Two periodic deterministic systems (Sine and Cosine);
・ Two random systems (Normal and Uniform).
Different combinations of these systems allow us to obtain pairs of series on which a priori independence could be expected, and other pairs in which a relationship would exist.
In the simulations arising from the systems of Henon, Ikeda, and Gopy (the three bi-dimensional) one of the two variables has been selected, except in those denoted “Henon x - Henon y” and “Ikeda x-Ikeda y”, in which we apply the test procedure to two series coming from the same system. In one of the experiments, we attempt to determine whether our test is capable of detecting the relationship existing between series of the same system, but with different embedding dimension7. In the experiment we denote as “Linear transformation”, a series obtained from the distribution N(0, 1) and a linear combination from this same series is used. Finally, as in the previous Section, we will use the series x and y of the Henon system affected by noise, and the series generated from the Henon - Ikeda coupled system.
Table 3 and Table 4 summarize the results obtained for the set of simulations, presenting the percentages of rejection of the null hypothesis of independence at the 5% significance level, and the average p-value.
Table 3 has been structured in two groups. The first corresponds to six pairs of systems in which a priori independence could be expected, while the second contains another six in which a relationship clearly exists.
The results obtained allow us to establish the following conclusions:
1) For the first group, the percentage of rejection is very small in all cases, always less than 8%. This indicates a good performance; when the null hypothesis of independence is true, it is rejected only a very small percentage of times. The average p-values are high in all cases, being in the range that would lead us to fail to reject the null hypothesis for any level of significance. The results are quite similar for the three sample sizes considered (the larger sample sizes improve the results of the test in some cases, but not all).
2) For the second group, the percentage of rejection is 100%, except in one case, in which it is 97.2%. In other words, the null hypothesis (which in this case is false) is rejected in practically all cases. Clearly, the average p-values obtained lead us to the same conclusion. These results provide clear evidence of interrelation between the pairs of series of this second group.
Table 4 shows, first, that our test is capable of detecting that the dependence between the series generated by the same system decreases when the noise level increases. Specifically, the result of the test shows that this
![]()
Table 3. Percentages of rejection of the null hypothesis of independence (α = 5%) and average p-values for the systems selected. Number of replicas = 500.
![]()
Table 4. Percentages of rejection of the null hypothesis of independence (α = 5%) and average p-values for the series of the Henon system affected by noise and the series of the Henon - Ikeda coupled system. Number of replicas = 500.
relationship is maintained until the level of noise is high (more than 80%). Second, for the coupled system, when the strength parameter increases, the percentage of rejections of the null hypothesis also increases. It is observed that, even for small levels of coupling, the existence of a relationship is detected in almost 100% of the cases.
These results suggest that our test procedure is robust in all studied situations. This good performance for simulated series indicates that it can be a useful tool for detecting possible interrelations or dependence between real series. This is the objective of the following section, in which we illustrate the application of our test procedure to some examples with economic series.
6. Application of the Test Procedure to Economic Series
In this Section, we use this methodology to analyze the possible interdependence between certain economic series. Specifically, we focus on two issues that have been dealt with through different approaches in the economic literature, on which there is consensus:
1) The relationship between inflation rate and nominal interest rates;
2) The relationship between employment and GDP.
We emphasize that we do not intend to study either of these questions in depth, which would require a broader and more thorough examination; our objective here is only to exemplify some of the possibilities and utilities offered by our test procedure.
6.1. The Relationship between Nominal Interest Rates and Inflation Rate
This relationship is widely studied in the literature, and has been dealt with from multiple points of view, for a broad range of variables. Regarding interest rates, different approaches have been used: nominal and real, ex-post and ex-ante, different maturity terms, diverse time frequencies… Similarly, the inflation rate can be the actual or the expected rate. In the case of considering the expected variables, questions associated with the formation of expectations also appear.
From among all the cases studied in the empirical literature, there is consensus on the existence of a positive relationship between the nominal interest rate and the actual inflation rate.
We now apply the methodology described in this work to monthly series of the US economy, to check whether or not this relationship is detected.
Specifically, we use the following series:
1) Nominal interest rates:
―Secondary market rate of the 3-month Certificate of Deposit, chosen as an example of a short-term interest rate. Period: January 1934 to March 2015.
―One year Treasury Constant Maturity Rate, a medium-term interest rate. Period: April 1953 to March 2015.
―Moody’s Seasoned AAA Corporate Bond Yield, representative of long-term interest rates. Period: January 1919 to March 20158.
2) Inflation rate: rate of the interannual variation of the CPI-U (Consumer Price Index for All Urban Consumers) published by the US Bureau of Labor Statistics.
Table 5 presents our results, clearly confirming the existence of a relationship between the three series of interest rates and the inflation rate for the chosen periods. The three p-values are zero, which means that the null hypothesis should be rejected for any level of significance.
We could consider whether this strong relationship would be maintained for certain sample sub-periods: a first period up to 1953, which includes the Great Depression and the two World Wars; a second period from 1953 to 1980; and a third period from 1980 to 2015. We consider that this third sub-period corresponds to a greater development of the financial markets, the appearance of new instruments, an increase in the level of information accessible to agents, and a high mobility of capital among countries.
The obtained results are shown in Table 6:
We observe that the existence of a relationship between the two variables is maintained for all the sub-periods considered. Nevertheless, we see a noticeable variability in the percentage of recurrence among the different series, as well as among the different sub-periods. In all cases, this indicator is somewhat higher in the second sub- period than in the other two. Additionally, if we discount the first sub-period, from which there is only information for one of the series, in general we notice that the relationship is greater for long-term interest rates. It is generally assumed that this is the rate that best responds to market forces, so it is reasonable that the relationship to the inflation rate is stronger. In any case, to study the causes of these results in depth, which we understand
![]()
Table 5. Application of the test to series of nominal interest rates against the series of the inflation rate.
![]()
Table 6. Application of the test to series of nominal interest rates against the series of the inflation rate for sample sub-periods.
would be of great interest, would require a much more detailed analysis. As we have previously mentioned, such an analysis lies beyond the scope of the present work.
6.2. The Relationship between Employment and GDP
This relationship is connected with the aggregate production function, which relates aggregate output to physical inputs or factors of production. Many theoretical and empirical works have been devoted to ascertaining the properties of the production function, and a broad agreement exists on some empirical relationships that this function must display. A widely accepted property of this function is that there is a nonlinear relationship between the quantities of productive factors and the amount of aggregate output obtained (i.e. that this function is nonlinear).
Next, we will apply our test procedure to check if this property is fulfilled in the
US
economy for labor input, and provide new empirical evidence. To do that, we will use the quarterly series of the real Gross Domestic Product (GDP), published by the US Bureau of Economic Analysis, and the series of the All Employees (total nonfarm), produced by the US Bureau of Labor Statistics9 (period: first quarter of 1960 to first quarter of 2015).
In the first row of Table 7, together with the results of our test, we also present the p-value of the Pearson correlation coefficient. This coefficient is a widely used tool to detect linear relationships between two variables. Its p-value (last column) is the probability of obtaining a correlation as large as the observed value by random chance, when the true correlation is zero.
We observe that both tests display the same result, both p-values are zero, which means the rejection of the null hypothesis for any significance level, and hence empirical evidence in favor of the existence of a relationship between GDP and employment.
In the second row, we present the results of the tests after filtering the linear component of the relationship. To do that, we fit a simple linear regression of the GDP on employment, and analyze the relationship between the residuals of this regression and employment. We observe that, in this case, the p-value of the correlation coefficient is equal to 1. This result is obvious, because if a regression model is computed correctly, the correlation coefficient between the residuals and the independent variable is zero.
However, the p-value of our test is still very small, so small as to reject the null hypothesis of independence for any usual significance level. Considering that one property of the regression models is that “the residuals have a nonlinear association with X if and only if the original observations of Y have a nonlinear association with X”, the conclusion will be that a nonlinear relationship exists between GDP and employment10.
This example is useful to show that our procedure can detect nonlinear dependence between variables, while other tests, such as the Pearson correlation coefficient cannot.
7. Conclusions
The main objective of this paper is to design a criterion that allows us to determine whether two series come
![]()
Table 7. Application of the test to the series GDP and Employment.
from independent dynamical systems. We develop our procedure on the basis of the Joint Recurrence Plot, and more specifically on its main quantitative indicator, the percentage of recurrence points. This indicator measures the level of dependence or synchronization existing between the series. The values of this indicator have a clear interpretation when they are extreme (very high or very low), but they are not so obvious for intermediate values. To solve this problem, we derive the probability distribution of the variable “number of recurrence points in the JRP” under the null of independence. This (exact) probability distribution allows us to determine a cut-off point from which determines whether the series present statistical dependence or not.
The performance of our procedure is analyzed through a simulation study for a broad set of systems in which, a priori, the existence, or not, of independence is evident. We have also applied it to series affected by increasing levels of noise, and to a pair of coupled systems with different degrees of coupling. The obtained results are very satisfactory and confirm the efficacy of the proposed method.
Finally, we use this methodology to study the empirical relationship between the nominal interest rate and the inflation rate, and between the GDP and the employment. In both cases, the results are clear, in line with the consensus on these issues in the existing literature. Moreover, in this latter case we have shown that our test is capable of detecting both linear and nonlinear relationships.
Acknowledgements
This work was supported by the Spanish Ministries of Science and Innovation [ECO2009-07936] and Economy and Competitiveness [ECO2013-41353-P], and by the Government of Aragon [Consolidate Group S10, Consolidate Group S21].
Appendix: A Brief Description of the Dynamic Systems Employed
This Appendix provides details of the equations that generate the dynamic systems used in our study.
As can be seen, in the unidirectionally-coupled Henon - Ikeda System, the Henon and Ikeda systems behave respectively as drive and response. Specifically, the variable x1 of the Henon system is coupled into the second equation of the Ikeda system, with ε being the “coupling strength”. Obviously, for ε = 0, drive and response would be independent.
NOTES
*Corresponding author.
![]()
1Although the theoretical fundamentals of this methodology are found in Sklar (1959) [4] , their application to the field of economics (specifically to finances) has not been relevant until recent years.
2It would also be possible to use a variable radius, different for each xi. In this case, the recurrence matrix would not be symmetrical. In [20] , different procedures to determine the radius are proposed.
![]()
3According to Romano (2004) [22] and Marwan et al. (2007) [23] , it could be said that the systems are “synchronized”.
![]()
4Nevertheless, in numerous experiments, we have confirmed that our results are very robust to the choice of the radius value.
5The equations of the dynamical systems used in this work are included in Appendix.
![]()
6See [26] .
7That is, applying the Time Delay Method proposed by Packard et al. (1980) [27] . This method transforms the original series into a series formed by m-tuples, m being the so-called embedding dimension. As is shown in Takens (1981) [28] , under certain conditions, both systems would be topologically equivalent.
![]()
8The three interest rates series are available on the Economic Research section of the Federal Reserve Bank of St Louis’s website.
![]()
9To eliminate the trend, we will take both series in differences.
10In our case, the GDP is clearly the dependent variable (Y) while the Employment is the independent variable (X).