On One Analytical Model of a Probability Estimation of Quality and Efficiency of Functioning of Complex Technical Queuing Systems

Ramaz R. Shamugia^1,2

¹Research Department of Radiophysics and Electronic Systems Modeling, Ilia Vekua Sukhumi Institute of Physics and Technology, Tbilisi, Georgia.
²Faculty of Informatics and Control Systems, Georgian Technicl University, Tbilisi, Georgia.

DOI: 10.4236/ijcns.2015.88029                

Abstract

The work is dedicated to the development of analytical model of probability estimation of reliability, productivity, quality and efficiency of functioning of the complex technical queuing system consisting of the arbitrary number of marked groups of the service devises (channels, facilities, servers) differing with reliable characteristics (parameters of refusals and restorations) of forming their composition (also of arbitrary number) marked, identical, unreliable and restorable serving channels in which for serving come in requirements with intensities depending on marking of channels. In the considered system it is supposed that the currents of refusals of serving devices and currents of coming requirements are subdued to Poisson, and the currents of restorations of refused devices and the currents of services of coming requirements—exponential laws of distribution of probabilities. A stochastic process of transfers of a system by that is Markovian process with continuous time and discrete states. Correlations linking the basic parameters and exit characteristics of the systems of the pointed out type are obtained in a view of probabilities of the system location in the given moment of time in one of the possible states.

Keywords

Multichannel Queuing Systems, QS with Unreliable Facilities, QS with Repairable Facilities, Servers with Failures, QS with Queues

1. Introduction

The end of the 20^th and beginning of the 21^st centuries were marked with rapid quantitative and qualitative growth of computer networks. This tendency that apparently will be kept in the nearest decades is well illustrated by unprecedented growth of the Internet network sweeping all countries of the world. Local computer networks that are the basis of automation of activities of separate enterprises and companies, and distributed computer networks involving cities, regions and continents penetrate all spheres of human activities including economics, science, culture, education, industry etc. Contemporary computer networks provide the consumers with a wide set of service including e-mail, transfer of fax and voice information, the work with distant data bases in the real scale of time, service of news and other services. On the basis of computer networks the following activities can be implemented: distant education, telemedicine, teleconferences, tele-exchanges, teleshops etc.

A quick growth of the number of computer networks, successes of fiber-optic and wireless means of communication are accompanied with a continuous change of the network technologies directed to the increase of fast activity and reliability of the networks, possibility of integrated transfer of the data, voice and video-information. The changing technologies, continuous quantitative and qualitative growth of computer networks make the following top-priority tasks: development of network designing fundamentals on the basis of systematization of already known approaches and development of new methods of analysis and synthesis of computer networks [1] - [4] . Theoretical methods of analysis and synthesis of computer networks found a reflection in numerous articles and separate sections of monographs [5] - [11] oriented mainly on mathematicians. Diversity and complexity of approaches, absence of systematization of basic directions in the analysis and synthesis of computer networks create considerable difficulties to designers who wish to apply theoretical approaches to the solution of practical tasks.

This article is dedicated to the development of one specific but the more generalized model of analysis and synthesis of computer networks that is based on the theory of systems and networks of mass service (theory of queues). The peculiarity of this model is the use of methods of theory of reliability for accounting of the reliable characteristics of serving devices. The article represents some perfections and generalizations of previous work of the author [12] - [14] . Choice of queuing theory as a method of model construction in the given article is connected with the fact that the stochastic characters of data arrival and its non-deterministic processing in communication units and channels predetermine the application of queuing theory models to computer network analysis and designing. The joint use of mathematical methods of the theory of system of mass service and theory of reliability provides the possibility of solution to numerous tasks of calculation of characteristics of the quality of functioning of various components of computer networks including the estimation of probable-time characteristics of units of commutation and routings; the analysis of productivity of local networks and networks with multiple access; the analysis of buffer memory of networks and methods of the local and global control of currents; calculation of losses and loading of the digital lines of communication during the transfer of data, voice and video-information at various methods of multiplexing etc. The analytical model developed in this article can be used for analysis of the network models of various levels of protocols corresponding to “the standard model of architecture of open systems” and models of the separate components of computer networks. They can be used for the calculation of integral characteristics at the global and local control of currents and also at the analysis of buffering process in the units of commutation packets that are the basic components of computer networks.

2. Purpose

Proceeding from the above said the purpose of our work is to develop research model for probability estimation of the factors of efficiency of real time, fail-proof and high-capacity systems, having equipment and time resources for maintenance of dependability and efficiency level and functioning in the conditions of influence of random factors―refusals, repairs, and random flow of random length tasks and random time of their service.

The proposed model is developed with consideration of the following assumptions:

・ Transitions of the system between different states is realized under shared effect of several random pro- cesses―processes of incoming and service of demands, as well as processes of refusals and repairs of service facilities:

・ The technical queuing system consists of 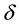(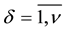;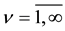) of various enumerated groups of serving channels (devices) while each group in its turn consists of 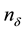identical serving devices;

・ Serving devices are subjected to stable refusals subdued to Poisson distribution of probabilities with the parameter of distribution 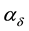depending on number of the group in which they are;

・ Stochastic process of restoration of refusing devices is described by exponential laws of distribution of probabilities with the parameter of distribution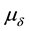, also depending on the group to which the restorable serving devices belong to;

・ The group of Poisson currents of requirements enter the system to be served with the intensity,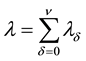

where 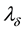is the intensity of current depending on the number of the group in which its service must take place.

・ The current of services of entering requirements is described by exponential law of distribution of probabilities and its intensity 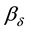also depends on the number of group;

・ In each group of serving devices it is foreseen the entrance collector for those requirements that will come in those moments of time, when the number of all correctly functioning devices in the given group are busy with serving of early coming requirements;

・ In any considered moment of time the length of the queue of requirements waiting for service in each group is determined as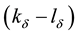, where 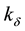is a total number of requirements, which are in 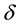-group of serving devices, and 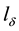is the number of requirements serving at the given moment, by having in the same group correctly functioning serving devices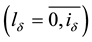, where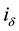―the number of correctly functioning at this moment of time, serving devices in 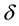-group.

For description of functioning of the above mentioned system in time, special probability functions

and have been introduced. By means of them we can describe the transition pro-

cesses of the system between the various states in accordance with the reasons causing these transitions― refusals and restorations of serving devices or entrance and service of requirements.

By those indexes, used in the markings of the pointed out probabilities, the number of group of serving devices are pointed out.

3. Introduction of Special Functions

The introduced functions are determined as follows:

is the probability of event at which at the moment t, -group of the system will be in a state

with functioning and refusing serving devices and at the same time, the total number of requirements being in the system will be equal to, from which the number of requirements being in serving, will be equal to, and requirements being in queue―will be equal to. The pointed out probabilities describe the process of change of system’s state in case of fixed values of upper indexes, reflecting the processes of entering and serving of requirements, i.e. and, and changing in time lower indexes, reflecting processes of refusals and restorations of serving devices, i.e. and.

is the probability of event at which in moment of time t, -group of serving devices will be in

state with functioning and refusing devices and at the same time, the total number of requirements being in group will be equal to, from which the number of requirements being in service, will be equal to, and the number of requirements being in queue―will be equal to―.

These probabilities describe the process of change of states of -group in case of fixed values of lower indexes determining the processes of refusals and restorations of devices, i.e. and, and changing in the time of upper indexes, reflecting the processes of entering and serving of requirements, i.e. and.

is the probability of event at which, in the moment of time t, -group of the system will be in

state with functioning and refusing devices and at the same time the total number of require- ments being in system, will be equal to, from which, the number of requirements being directly in serving, will be equal to, and the number of requirements being in queue―will be equal to.

These probability functions describe the process of change of the state of system at permanently changing upper and lower indexes, i.e., and,.

Rate fixing condition has the following form:

In order to determine intensities of system transitions at fixed values of upper indices and, the following designations are introduced:

is the intensity of system transition being in moment t in state, into one of the possible states, , or caused with refusal of restoration of serving device;

is the intensity of system transition being in moment t in state, into neighboring state caused with the restoration of service device;

is the intensity of system transition being in moment t in state into neighboring state caused with the refusal of service device;

In order to determine intensities of system transitions at fixed values of lower indices and, the following designations are introduced:

is the intensity of system transition being in moment t in state into one of the possible states or caused with income and service of regular request;

is the intensity of system transition being in moment t in state into neighboring state caused with income of regular request;

is the intensity of system transition being in moment t in state into neighboring state caused with serving of regular request;

Considering the possible changes of the system in infinitely small time interval, with the help of above introduced probabilities, on the basis of probability reasoning, the following system of difference equations can be written describing the process of system functioning in time in assumption of fixed values of upper indices and:

(1)

(2)

where

(3)

Summands entering in the right part of equality (3) should be obtained by solution of the following system of difference equations which describes the process of functioning of the considered system in assumption of fixed values of lower indices and:

(4)

(5)

Below we define sense of the notion of probabilities in Equations (1)-(3):

is the probability of the event when the system being in time moment t in one of the possible states, , or, in moment will happen in state, {quantity of devices: operable―, inoperable―; quantity of requests: general

quantity―,―in service, in queue for service}. In the given case it is supposed that transitions between system states are realized due to request income and their service at fixed values of lower indices i and (i.e. parameters of refusals and repairs of service devices);

is the probability of the event when the system being in time moment t in one of the possible states or in moment will happen in state

{quantity of devices: operable―, inoperable―; quantity of requests: general quantity―,―in service, in queue for service}. In the given case it is supposed that transitions between system states are realized due to refusals and repairs of service devices at fixed values of upper indices and (i.e. parameters of request income and their service);

is the probability of the event when the system with probability being in moment t in state {quantity of devices: operable―, inoperable―; quantity of

requests: general quantity―,―in service,―in queue for service} in time with probability

will not go over to neither of possible states and will stay in the former state;

is the probability of the event when the system with probability being in moment t in state {quantity of devices: operable―, inoperable―; quantity of requests: general quantity―,―in service, in queue for service} in time with probability will not go over to state;

is the probability of the event when the system with probability being in moment t in state {quantity of devices: operable―, inoperable―quantity of requests: general quantity―,―in service, in queue for service) in time with probability will go over to state;

is the probability of the event when the system with probability being in moment t in state {quantity of devices: operable―, inoperable―; quantity of

requests: general quantity―,―in service, in queue for service) in time with probability

will not go over to neither of possible states and will stay in the former state;

is the probability of the event when the system with probability being in moment t in state {quantity of devices: operable―, inopera-

ble―; quantity of requests: general quantity―,―in service, in queue for

service} in time with probability will go over to state;

is the probability of the event when the system with probability being in moment t in state {quantity of devices: operable―, inoperable―; quantity of requests: general quantity―,―in service, in queue for service) in time with probability will go over to state.

From Equations (1)-(3) by going to limit at we obtain the following recurrence differential equations:

(6)

(7)

where

(8)

(9)

(10)

Here:

,

.

Systems of Equation (6), Equation (7), Equation (9) and Equation (10) represent the systems of inhomogeneous differential equations with fixed factors.

In assumption of given starting conditions:

partial solutions of these equations can be retrieved by method of operational calculus using the following Laplace transformations:

Systems of Equations (6)-(10) in Laplace derivatives will get the following form:

(11)

(12)

where

(13)

(14)

(15)

After simple transformations, Equations (11)-(15) are transformed into inhomogeneous systems of algebraic equations which are solved quite simply with Cramer formulas relative to and:

(16)

(17)

where

(18)

(19)

(20)

With the help of Cramer formula the solution of Equation (20) can be written in the following form:

(21)

where

(22)

is a principal determinant of system (20), while are determinants received by substitution of the

right part (1/s) of equation system (20) into -th column of matrix. Here = 1 - 3 are the numbers of matrix columns.

The solutions of the system of Equation (17) are written similarly:

(23)

where

(24)

is a principal determinant of system (17), while are determinants received by substitution of the

right part of equation system (12) into -th column of matrix. Here, as above = 1 -

3 are the numbers of matrix columns.

With the help of found probabilities of states it is easy to determine different factors of dependability and efficiency of the examined system.

4. Conclusions

The results obtained in this work represent some generalizations of already known in literature results, including the results developed by the author of this article [13] [14] , which can be considered as private cases. They enable to calculate probabilities of possible states of the above described system via which it will be possible to express other significant indices of reliability, productivity, quality and effectiveness of functioning of such systems.

Severity of given mathematical judgments and transformations, taking into account the assumptions made in this work, as well as the approach to the exposition of material, may serve as proving the adequacy of the offered model. The novelty of the model and its more general nature is confirmed by the fact that in case of some assumptions about model’s parameters, we will get the new models coinciding with the already known ones in the literature.

The work results can be successfully used during the analysis and synthesis of such complex technical systems as the system of the data transfer, system of cell communication, computer and communication networks, flexible production lines, automation control systems and also other complex technical systems used both in civil and military objectives. They can be used during estimation of the given or provision of the required levels of reliability, productivity and effectiveness of functioning of complex technical systems both on the stage of operation and the stage of designing.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Gnedenko, B.V. and Kovalenko, I.N. (2012) Introduction to Queuing Theory. LKT, 400.
[2]	Saati, T.L. (1965) Elements of Queuing Theory and Its Application. Sov. Radio, 510.
[3]	Cherkesov, G.N. (1974) Dependability of Technical Systems with Time Redundancy. Sov. Radio, 296.
[4]	Feller, W. (1971) An Introduction to Probability Theory and Its Applications. Vol. 2, John Willey and Sons, New York, 766.
[5]	Kulgin, M. (2000) Technology of Corporative Networks. SPb, “Peter” Publishing House, 704.
[6]	Lazarev, V.G. (1996) Intellectual Digital Networks. Finances and Statistics.
[7]	Martin, D., Chapman, K. and Liben, D. (2000) ATM. Architecture and Realization. “Dori” Publishing House, 213.
[8]	Nazarov, A.N. and Simonov, N.V. (1998) ATM Technology of High Speed Networks. “ECO-TRENDT” Publishing House.
[9]	Basharin, G.P., Bacharov, P.P. and Kogan, Y.A. (1989) Analysis of Queues in Computing Networks. Theory and Methods of Calculation. “Nauka” Publishing House.
[10]	Bacharov, P.P. and Penichkin, A.V. (1998) Theory of Mass Service. “Russian University of Peoples’ Friendship” Publishing House.
[11]	Yershov, M.A. and Kuznetsov, N.A. (1995) Theoretical Fundamentals of Construction of the Digital Network with Integration of Services. IPPI RAN.
[12]	Khurodze, R.A., Shamugia, R.R. and Kukava, R.R. (2006) Research of Dependability Characteristics of Technical Systems with Equipment and Time Duplications. Bulletin of the Georgian National Academy of Sciences, 174, 110-113.
[13]	Shamugia, R. (2014) On One Model of Multichannel Queuing System with Unreliable Repairable Servers and Input Memory. Int’l J. of Communications, Network and System Sciences, 7, 279-285. http://dx.doi.org/10.4236/ijcns.2014.78030
[14]	Shamugia, R. (2014) On One Model of Complex Technical Queuing System with Unreliable Devices and with Time Redundancy. Int’l J. of Communications, Network and System Sciences, 7, 257-264. http://dx.doi.org/10.4236/ijcns.2014.78028