Mathematical Content Understanding for Teaching: A Study of Undergraduate STEM Majors ()
1. Introduction
This paper investigates the nature of mathematical understanding that is needed to teach three foundational early algebra topics. Subject matter knowledge plays a central role in teaching (Buchmann, 1984). Teachers’ understanding of mathematics is central to their capacity to carry out instructional activities such as using instructional materials wisely, assessing students’ progress, and making sound judgments about presentation, emphasis, and sequencing (Ball, Hill, & Bass, 2005) .
Despite the fact that subject matter knowledge is central to teaching, content knowledge rarely figures prominently in research or teacher preparation programs (Ball, 1990; Harel, 1993) . Shulman (1986) regarded content as “the missing paradigm” in research on teaching. To address this “missing paradigm” on teaching, Shulman proposed several types of knowledge teachers need in order to teach. One critical type of knowledge is “pedagogical content knowledge” (PCK), which he defined as “the ways of representing and formulating the subject that make it comprehensible to others” (p. 9). Since then, educational scholars have attempted to measure PCK and link it to student learning (e.g., Ball, Hill, & Bass, 2005; Baumert et al., 2010 ).
Scholars have conceptualized PCK in different ways. For instance, Ball and her colleagues further elaborated Shulman’s PCK as consisting of different dimensions such as knowledge of content and students, knowledge of content and teaching, and knowledge of content and curriculum (Ball, Hoover, & Phelps, 2008). Ma (1999) calls teachers’ subject matter knowledge “profound understanding of school mathematics”. Schoenfeld and Kilpatrick (2008) regard this kind of content understanding as “knowing school mathematics in depth and breadth”.
These scholars’ work has crystallized the concept of PCK. However, there are several directions in which further research is needed. First, it is important to delineate the depth and breadth of the relevant knowledge for key topics in the curriculum (Schoenfeld & Kilpatrick, 2008) . Second, most work on mathematics teachers’ subject knowledge has focused on elementary to middle grades (e.g., Ball, Hill, & Bass, 2005; Ma, 1999 ), but not much work has focused on foundational algebra topics. Finally, Ball and her colleagues (2008) stressed that further work was needed on specialized content knowledge “in order to understand the most important dimensions of teachers’ professional knowledge” (p. 405).
Our work builds on these scholars’ research, but extends the existing research base in two important ways. First, it makes a deliberate effort to focus on three critical and foundational mathematics topics for learning algebra. Secondly, it intends to make explicit the key mathematical ideas underlying each topic that are the foundation for what Shulman (1986) calls “the content of the lessons taught”. The three topics we focus on are dividing fractions, linear equations in two variables and their graphs, and quadratic functions and their graphs. These topics have been chosen for several reasons. First, they are foundational topics in early algebra; yet they are challenging for teachers to teach well and for students to grasp. Second, there exist substantial misunderstandings (or incoherent portraits) of these topics in many textbooks. Finally, these topics occupy a significant part of the curriculum from grades 5 through algebra 1.
This paper is structured as follows. We begin with a review of relevant research literature concerning teachers’ mathematical knowledge for teaching. Building on prior research, we outline and elaborate a framework for examining the nature of mathematical understanding of the three topics that are the focus of this study. We then describe various aspects of the inquiry methods we have used to investigate a sample of undergraduate STEM majors’ mathematical understanding based on our framework. Following this, we present our findings on the characteristics of these STEM majors’ mathematical understanding of the three topics. Finally, we discuss the implications of our findings for pre- and in-service mathematics teachers’ content training.
2. Review of Literature
In his 1985 presidential address at the annual meeting of the American Educational Research Association, Shulman (1986) described content as “the missing paradigm” in research on teaching and argued that critical questions had not been asked. These questions include: Where do teachers’ explanations come from? How do teachers decide what to teach, how to represent it, how to question students about it, and how to handle students’ misunderstanding?
To address this “missing paradigm” on teaching, Shulman proposed several types of knowledge teachers need in order to teach. One critical type of knowledge is “pedagogical content knowledge” (PCK), which he defined as “the ways of representing and formulating the subject that make it comprehensible to others” (p. 9). Since then, educational scholars have attempted to elaborate what PCK may entail and link it to student learning (e.g., Ball, 1990; Ball, Hill, & Bass, 2005; Ball, Hoover, & Phelps, 2008; Baumert et al., 2010; Schoenfeld & Kilpatrick, 2008 ).
One theoretical framework of proficiency in teaching mathematics came from Schoenfeld and Kilpatrick (2008) . Their framework consists of several dimensions, the first dimension being “knowing school mathematic in depth and breadth” (p. 2). Schoenfeld and Kilpatrick (2008) argue that proficient teachers’ knowledge of school mathematics is both broad and deep. The breadth focuses on teachers’ ability to have multiple ways to conceptualize the content, represent the content in various ways, understand key mathematical ideas, and make connections among mathematical topics. The depth, on the other hand, refers to teachers’ understanding of how the mathematical ideas grow conceptually from one grade to another. With knowledge that is both broad and deep, teachers will be able to prioritize and organize content focusing on big mathematical ideas and to respond flexibly to students’ questions (Schoenfeld & Kilpatrick, 2008) .
The characteristics of content understanding outlined in Schoenfeld and Kilpatrick’s framework are similar to the ideas rooted in a series work by Deborah Ball and her colleagues (Ball, 1990; Ball, Hill, & Bass, 2005; Ball, Hoover, & Phelps, 2008) . Ball and her colleagues call the kind of content understanding described by Schoenfeld and Kilpatrick, “mathematical content knowledge for teaching” (Ball, Hill, & Bass, 2005; Ball, Hoover, & Phelps, 2008) . In her earlier work, Ball (1990) proposed four dimensions of subject matter knowledge for teaching that mathematics teachers need to have. These dimensions include: (1) possessing correct knowledge of concepts and procedures; (2) understanding the underlying principles and meanings; (3) knowing the connections among mathematical ideas; and (4) understanding the nature of mathematical knowledge and mathematics as a field (e.g., being able to determine what counts as an “answer” in mathematics? What establishes the validity of an answer?, etc.).
In the work that followed, Ball and her colleagues (Ball, Hill, & Bass, 2005) defined “mathematical content knowledge for teaching” as being composed of two key elements: “common” knowledge of mathematics that any well-educated adult should have and mathematical knowledge that is “specialized” to the work of teaching and that only teachers need know” (p. 22). From their descriptions, it seems that “common” mathematical knowledge is equivalent to being able to do mathematics, whereas “specialized” mathematical knowledge consists of being able to do mathematics and to know why (i.e., the reasoning that teachers need to know in order to teach students).
The notion that there is content knowledge unique to teaching is further expanded in their most recent work. Ball and her colleagues (Ball, Thames, & Phelps, 2008) proposed a sub-domain of “pure” content knowledge unique to the work of teaching, which they call specialized content knowledge (italics emphasized by the authors). The distinction between specialized content knowledge and other knowledge of mathematics, according to the authors, is that the former is needed by teachers for specific tasks of teaching (e.g., responding to students’ why questions) and is not intertwined with knowledge of pedagogy, students, curriculum, or other non-content domains. While appealing, Ball and her colleagues point out that this specialized content knowledge needs further work. This sentiment is echoed by Schoenfeld and Kilpatrick (2008) who suggest further work be done to delineate the depth and breadth of the relevant knowledge for key topics in the curriculum. Our work is an attempt to describe what the specialized content knowledge may entail for three key early algebra topics.
The premise of our work is that mathematics taught to students at the K-12 level differs significantly from that taught in university mathematics courses. This stance has been emphasized by research mathematicians who have worked with the mathematics education community (Wu, 2011a) and educators alike (e.g., Ball, 1990 ). It supports the argument that the mathematical development of topics to K-12 students must be sensitive to their knowledge base and mathematical sophistication (Wu, 2011a) . These ideas put forward by research mathematicians echo, to some extent, those proposed by educational scholars (e.g., Ball, 1990; Ball et al., 2008; Ma, 1999; Schoenfeld & Kilpatrick, 2008; Shulman, 1986 ) in terms of the specialized content knowledge for teaching K-12 students. In addition, the argument has some empirical support. As Ball and her colleagues found (Ball et al., 2005) that students of third grade teachers who did well on their measure of mathematical content knowledge for teaching performed better than those with teachers who did not do so well on their measure.
In contrast to Ball and her colleagues who attempted to measure teachers’ content knowledge for teaching, most scholars typically measure the adequacy of secondary mathematics teachers’ content knowledge by the amount of college mathematics coursework they have completed as undergraduates (i.e., college major in mathematics signals extensive mathematics coursework). The implicit assumption is that typical college-level mathematics courses teach future teachers what they need to know in order to teach at the 6-12 grade level. As pointed out earlier, this assumption has been challenged by teacher educators (e.g., Ball, 1990; Shulman, 1999 ) and mathematicians (e.g., Wu, 2011a ).
Empirical studies on the relationship between teachers’ college mathematics coursework and their students’ mathematical performance have produced mixed results. Some studies have found that teachers with degrees in mathematics have a significant positive effect on high school students’ mathematics test scores (Goldhaber & Brewer, 1997, 2000; Rowan, Chiang, & Miller, 1997) . Other studies have shown that teachers with extensive college-level mathematics coursework do not necessarily know how to explain fundamental K-12 concepts such as the reasoning behind the invert-and-multiply rule for division of fractions (Ball, 1990; Borko et al., 1992). These findings lend further support to the argument that the content of college mathematics course has little to do with the content taught at K-12 level.
The paradox begs the question: What is the nature of mathematical content understanding that is needed in order to teach middle school and high school mathematics? What does this mathematical content understanding look like? This paper addresses these questions through an empirical study of a sample of undergraduate STEM majors at one of the research universities in the west coast of the United States. Specifically, we ground our work in the three mathematical topics identified previously.
What might this specialized content knowledge look like for the mathematical topics we focus on in this study? We elaborate this in the next section, but first we outline in Table 1 the characteristics that exemplify this specialized content knowledge from mathematical perspectives.
The three characteristics are derived from the five “fundamental principles of mathematics” proposed by research mathematicians (e.g., Wu, 2010a ) and the key ideas proposed by researchers whose work focuses on mathematics education (e.g., Schoenfeld & Kilpatrick, 2008 ). These characteristics of content understanding are consistent with and reflect the mathematics education community’s call for a profound understanding of school mathematics for teaching (e.g., Ball, 1990; Ma, 1999; Schoenfeld & Kilpatrick, 2008 ). One point we want to emphasize is that we describe some of the relevant knowledge, acknowledging that there are various ways to conceptualize the content, and more than one way to approach the teaching of it ( Cochran-Smith & Lytle, 1999 ).
3. Content Understanding for Teaching: Dividing Fractions, Linear Equations, and Quadratic Functions
In this section, we elaborate what exemplary content understanding looks like for teaching dividing fractions, linear equations, and quadratic functions. By exemplary, we mean the understanding exhibits the three characteristics outlined in the previous section.
To examine prospective teachers’ mathematical understanding, we used a series of teaching scenario questions, focusing on the three previously mentioned mathematics topics (see Table 2 for the questions). These scenario questions are intended to measure prospective teachers’ mathematical understanding for teaching grades 6 through 12. The thinking behind the design of these scenario questions is broadly informed by scholarly work from teacher education and mathematics education (e.g., Ball, Thames, & Phelps, 2008; Ma, 1999; Schoenfeld & Kilpatrick, 2008 ) and mathematics (e.g., Wu, 2010a, 2011b ).
3.1. Key Mathematical Ideas Underlying Each Topic
To provide a roadmap guiding our focus, Table 2 lists the critical mathematical ideas and concepts underlying our scenario questions for each of the three topics.
With these key mathematical ideas in mind, we now elaborate what an exemplary content understanding for teaching these topics might look like in terms of exhibiting precision, coherence, and purposefulness. In the interest of page limit, we discuss the topic of “dividing fractions” in depth while leaving the other two, linear equations and quadratic functions, in Appendix A and Appendix B respectively.
3.2. Dividing Fractions
3.2.1. What Does Dividing Fractions Mean?
We used scenario questions 1.1 and 1.2 (see Table 2) to get at participants’ understanding.
![]()
Table 1. Characteristics exemplify content knowledge for teaching.
![]()
![]()
Table 2. Focus and key mathematical ideas underlying the scenario questions for each topic.
An exemplary response to these questions clearly exhibits characteristics of precision, coherence, and purposefulness. Consider the following response. Note that the response shows a deliberate effort at invoking students’ prior mathematical knowledge and familiarity with whole numbers:
In order to build on students’ prior knowledge of whole numbers, we assume that students have been exposed to the definition of a whole number as a point on the number line. This way of defining whole numbers will put whole numbers and fractions on the same footing in the real number system, which will make the subsequent teaching of dividing fractions a little easier if students are helped to see the parallel logic of dividing whole umbers and that of dividing fractions. So before I teach students how to set up the problem and solve it, I would first ask questions such as: What is a whole number? Can you give me some examples of whole numbers? What about some examples where whole numbers are used to describe quantities of things? Etc.
Here, the response shows a deliberate effort at scaffolding mathematical ideas by emphasizing the need to help students see the connection between how whole numbers and fractions are defined. In addition, the response is very purposeful and clear about what numbers and fractions are and about helping students see the “parallel logic” between the two. The purposefulness and clarity paves the way for easier grasping of a new topic (i.e., dividing fractions) based on prior knowledge (i.e., dividing whole numbers). As the response continues:
After this initial questioning and answering exercise, I would pose the following problem to students: A rope of 44 meters long is cut into pieces which are each 2 meters long. How many such pieces can we get out of the rope? Sixth graders probably are well trained enough to immediately figure out what they need to do (i.e., 44 ÷ 2 = 22). After they have done the division and get an answer, I would ask them to explain why they divide? What does the definition of division of whole numbers mean? How can we represent this on the number line? Etc. The key mathematical ideas I hope to reach common understanding among students are: (1) Dividing two whole numbers A ÷ B means that there is a unique whole number C that makes C ´ B = A true. In this context, it means 22 ´ 2 = 44, or 44 = 22 ´ 2; (2) Division is an alternative way of writing multiplication (i.e., A ¸ B = C is an alternative way of writing ´ B = A); and (3) Using the number line to graphically represent what dividing 44 ÷ 2 means (i.e., if we cut the rope of 44 meters into pieces that are 2 meters each, 22 is the 22nd point on the number line (when counting by 2 meters) and coincides with the 44 meter point.
Note here again the response is deliberate at connecting what students knew (i.e., dividing whole numbers) with what they are about to learn (i.e., dividing fractions). Furthermore, the response uses definition as a basis for logical reasoning (what does dividing fractions mean?) behind why divide. In addition, the response demonstrates the understanding of the interconnectedness of mathematical ideas. In this case, the response emphasizes the algebraic (44 ÷ 2) and the geometric representations of dividing whole numbers using the number line. Finally, note how the response emphasizes the key mathematical ideas that students should be able to walk away with. With this solid foundation, students are ready to set up the problem as one that involves dividing fractions, as shown below:
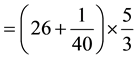
Building on these key mathematical ideas related to whole numbers, I would then point out to students that, since fractions are points on a number line, what we can do with whole numbers, we can do the same with frac-
tions. Hopefully students then will be able to set up the problem as: 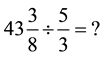 At this point, students have to
At this point, students have to
be taught at least how to divide fractions (i.e., at least the mechanics of dividing fractions have to be taught
prior to the lesson of solving this problem) so that they can carry out the calculation, which give s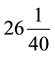 . Of
. Of
course, students should be helped to understand why they invert and multiply (this part will be picked up in scenario 1B).
Here again the response emphasizes a key idea (i.e., since fractions are points on a number line, what we can do with whole numbers, we can do the same with fractions). This emphasis helps students see the interconnectedness between dividing whole numbers and dividing fractions. Furthermore, the response is deliberate at scaffolding these ideas by invoking students’ prior mathematical knowledge. So what does dividing fractions mean?
So how do we interpret what we got in this particular problem’s context? Two key ideas underlie this question: (1) first is to remind students that division is an alternative way of writing multiplication, and (2) distributive law. Therefore, I would ask students what would be an alternative way to write:
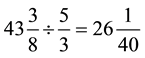
Building on what we talked about using the whole numbers (i.e., 44 meters long rope cut into pieces 2 meters long each), students probably will be able to write down:
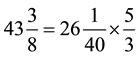
 ¬definition of mixed number (a sum of a whole number and a proper fraction)
¬definition of mixed number (a sum of a whole number and a proper fraction)
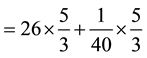 ¬distributive law
¬distributive law
So the expanded expression means that, when we cut the rope into pieces that are 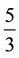 meters each, we get 26 pieces of
meters each, we get 26 pieces of 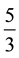 meters segment, plus a fraction of a
meters segment, plus a fraction of a 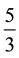 meters segment (i.e.,
meters segment (i.e., 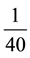 of
of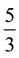 ).
).
Here again the response is purposeful about emphasizing key mathematical ideas (Two key ideas underlie this question) and about scaffolding from simple to complex (i.e., Building on what we talked about using the whole numbers, i.e., 44 meters long rope cut into pieces 2 meters long each). In addition, the response is keen on using the definition (i.e., division as a different but equivalent way of writing multiplication) as the basis for logical reasoning that leads to an understanding of what dividing fractions means. Furthermore, as shown in Figure 1, the response emphasizes that students see how dividing fractions can be represented on the number line:
What does this look like on the number line? I would have students draw the number line and set out the total
length of  meters. Then from the origin (i.e., 0), taking segments of
meters. Then from the origin (i.e., 0), taking segments of 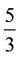 meters, we would get 26 whole pieces or segments of
meters, we would get 26 whole pieces or segments of ![]() meters. In other words, the 26th point is the number
meters. In other words, the 26th point is the number![]() . The fraction part,
. The fraction part, ![]() of
of ![]() means we divide the next
means we divide the next ![]() segment into 40 equal parts, and the 1st point (as we count from the left endpoint of this
segment into 40 equal parts, and the 1st point (as we count from the left endpoint of this ![]() segment) is the fraction part
segment) is the fraction part ![]() of
of ![]() and has length
and has length![]() . This final point represents the number
. This final point represents the number![]() , which coincides with the point
, which coincides with the point ![]() on the number line.
on the number line.
Here again the response demonstrates the interconnectedness of mathematical ideas by emphasizing the multiple representations (i.e., algebraic and geometric) of what dividing fractions mean.
In summary, this exemplary response consistently emphasizes the key mathematical idea, its rationale, the logical progression of mathematical concepts, and the connectedness among different mathematical concepts, procedures, and ideas. In addition, the response shows attention to how to scaffold mathematical ideas to students (e.g., from simple to complex; from specific to general). Overall, the response exemplifies precision, coherence, and purposefulness, the key principles that characterize content understanding for teaching.
3.2.2. Why Invert and Multiply When Dividing Fractions?
Though most know the invert and multiply rule when dividing fractions, few understand why invert and multiply works. We used scenario question 1.3 (see Table 2) to get at participants’ understanding of the invert and
![]()
Figure 1. Representation of dividing fractions on the number line.
multiple rule when dividing fractions.
An exemplary response to this scenario question begins with explicit definition of what dividing fractions means, as shown below:
First, I would help the student review what ![]() means―i.e., what does it mean to divide fractions? Using the number line again, set out
means―i.e., what does it mean to divide fractions? Using the number line again, set out![]() ; how many
; how many ![]() do we get? What is another way of writing this division problem? Etc. Therefore, by the definition of dividing fractions
do we get? What is another way of writing this division problem? Etc. Therefore, by the definition of dividing fractions ![]() can be written as:
can be written as: ![]() (a unique fraction)
(a unique fraction)![]() .
.
With the meaning of dividing fractions defined, the response proceeds to the logical next step, that is, what is this unique fraction?
So how do we know what this unique fraction is in this context? Since ![]() then
then![]() .
.
Can I re-write the above equation as:![]() ? Yes, because of the associative law of multiplication. Now, look at this new equation. What does it remind you? Compare it to the definition of division (i.e.,
? Yes, because of the associative law of multiplication. Now, look at this new equation. What does it remind you? Compare it to the definition of division (i.e., ![]() can be written as
can be written as ![]() (a unique fraction)
(a unique fraction)![]() ). Is
). Is ![]() a solution to
a solution to![]() (a unique fraction)
(a unique fraction)![]() ? Yes, that’s what the equation above shows.
? Yes, that’s what the equation above shows.
Using the definition of dividing fractions, the response connects the definition with the solution as a way to help the student make an inference that ![]() is the unique fraction. But the response is very precise about the definition, because how do we know
is the unique fraction. But the response is very precise about the definition, because how do we know ![]() is the only solution?
is the only solution?
Now, how do we know ![]() is also a unique solution? Is it possible that a different solution (i.e., frac-
is also a unique solution? Is it possible that a different solution (i.e., frac-
tion) exists out there? How do we know for sure? Suppose there is a different solution. Let’s call our solution C and let’s call this different fraction C’. What would happen? At this point, I would work with this student to reason through (i.e., prove) that the solution is unique:
If ![]() then
then![]() by the distributive law.
by the distributive law.
What does this say about C and C’? The conclusion is C and C’ must be the same fraction.
So by definition ![]() is the unique fraction or solution to this division problem
is the unique fraction or solution to this division problem![]() , which is where “invert and multiply” comes from.
, which is where “invert and multiply” comes from.
Here the response again uses the definition to help the student reason that ![]() has to be the unique
has to be the unique
fraction through falsification (i.e., assuming it is not and arriving at a contradictory conclusion to what is given).
In addition to exemplify the reasoning process by using explicit definitions, an exemplary response also exhibits coherence in terms of being deliberate at scaffolding mathematical ideas from simple to complex and specific to general, as shown below:
After working through this specific problem with the student, I would also help him see the general principle
(i.e., “invert and multiply” works for dividing all fractions) using symbols. Let ![]() and
and ![]() be fractions where m, n, k, l are whole numbers and n, k, l are nonzero. Then the goal is to prove
be fractions where m, n, k, l are whole numbers and n, k, l are nonzero. Then the goal is to prove![]() . The key is to enable
. The key is to enable
the student to see that the reason why the particular division problem above (i.e., concrete numbers in the scenario) works is exactly the same when the specific numbers are replaced with symbols that stand for whole numbers:
Note the response is purposeful about what they are doing, emphasizing the goal of the mathematical activity
(the goal is to prove![]() .) and the key idea (The key is to enable the student to see that the reason why
.) and the key idea (The key is to enable the student to see that the reason why
the particular division problem above (i.e., concrete numbers in the scenario) works is exactly the same when the specific numbers are replaced with symbols that stand for whole numbers). Apart from purposefulness, the response here is also helping students make a connection between something unfamiliar (i.e., using symbols) with something familiar (i.e., using concrete fractions). By emphasizing coherence, the response helps the student see the interconnectedness of mathematical ideas.
Just as![]() , we have
, we have![]() . Therefore:
. Therefore:
![]()
![]()
![]() ¬associative law of multiplication
¬associative law of multiplication
![]() ¬product rule for fraction multiplication
¬product rule for fraction multiplication
So what is![]() ? This is the multiplication representation of dividing the two fractions
? This is the multiplication representation of dividing the two fractions ![]() and
and![]() ; or put it in a different way, it’s the definition of dividing fractions:
; or put it in a different way, it’s the definition of dividing fractions: ![]() is defined as
is defined as ![]() so because
so because ![]() we conclude
we conclude ![]() by the uniqueness of
by the uniqueness of ![]() (proven above).
(proven above).
By the product rule for fraction multiplication, ![]() , which is how we get the general “invert and multiply” rule:
, which is how we get the general “invert and multiply” rule:
![]()
Again in this example, we see how the responses exemplify precision, coherence, and purposefulness, the key principles that characterize content understanding for teaching.
To summarize, we analyze in this section what exemplary mathematical content understandings of the key early algebra topics look like and describe key attributes that characterize such understandings. As can be seen in the examples, they exemplify precision, coherence, and purposefulness. There is consistent and substantial evidence of an attempt to emphasize the key mathematical idea, its rationale, the logical progression of mathematical concepts, and the connectedness among different mathematical concepts, procedures, and ideas. In addition, these responses pay a deliberate attention to scaffolding mathematical ideas to students in a systematic and coherent way, from simple to complex and from specific to general.
To what extent do the sampled students in our study exhibit such understanding? What does their current understanding of these topics look like? We address these questions in the following sections. But first, we present the background information on the study.
4. Methods
4.1. Research Site and Study Sample
The study took place at a west coast research university. Study participants were recruited from undergraduate courses that focus on K-12 mathematics and mathematics teaching and learning. Of the 46 students who responded to the scenario questions, 32 (70%) gave active consent to use their responses for research. Of these 32 study participants, 5 (16%) were science majors, 4 (13%) were engineering majors, 16 (50%) were mathematics majors, and 7 (22%) were humanities majors; 8 (25%) were transfer students from two-year colleges. The 14 students who did not give active consent were all STEM (Science, Technology, Engineering, and Mathematics) majors, of which 9 (69%) were mathematics majors. However, their score distributions did not differ significantly from those of the study sample. The sample had seven humanities majors. Their inclusion did not affect the findings of the study.
4.2. Data Collection
We collected two rounds of data, in spring 2010 and spring 2011. At each data collection occasion, one of the researchers visited the study participants’ classes. The research member explained the purpose of the study and distributed the form containing the scenario questions. In spring 2010, respondents were given about two weeks to finish the form. Based on the preliminary analysis of data collected in spring 2010, we reduced the number of scenario questions (without sacrificing the opportunity to assess respondents’ understanding of key mathematical concepts) and collected additional data in spring 2011. At the spring 2011 occasion, respondents answered the scenario questions during a 2-hour class period.
4.3. Data Analysis
In scoring a respondent’s responses to a scenario question, we focus on the quality of the reasoning process. Specifically, the quality of the reasoning process is judged by the three characteristics that exemplify content understanding for teaching outlined in Table 1. These three criteria are the basis for the scoring rubric as shown in Table 3.
Using this rubric, responses to each scenario question were scored on a scale of 1 to 3 (blank responses were categorized as missing data and no one in the sample scored 4). A correlation matrix of the scores was then produced, and score frequencies for each question were examined by college major. To analyze performance by topic, scores on the scenario questions related to the same topic were averaged; the correlations between the mean scores were then examined, and means were compared according to college major. For the qualitative analysis, the quality of reasoning between high scores (i.e., 3) and low scores (i.e., 2 or 1) were compared based on the three criteria described above.
![]()
Table 3. Rubrics for scoring content understanding for teaching.
5. Findings
We first present some quantitative data to show the distribution of students’ rating scores. We then describe the variation and qualitative difference in their responses to demonstrate the characteristics of their content understanding on the three topics.
5.1. Distribution of Student Scores
As shown in Table 4, of the 32 study participants, 18 scored only 1’s across all of the scenario questions, eight scored a combination of 1’s and 2’s, five scored a combination of 1’s, 2’ s, and 3’s, and only one scored 3’s across all of the scenario questions and none scored 4.
Further analysis of the six participants who scored 3’s on any of the scenario questions shows that they were mathematics majors taking Mathematics of the Secondary School Curriculum, a three-course sequence designed to address the mathematics curriculum of grades 6 - 12. For example, on each dividing fractions question, two to four of the nine mathematics majors who were enrolled in the Mathematics of the Secondary School Curriculum scored 3 whereas the seven non-mathematics majors and the one mathematics major not enrolled in the Mathematics of the Secondary School Curriculum scored at most 2.
The score patterns of fraction questions were similar for the questions related to linear equation in two variables and the questions related to quadratic function. Overall, only mathematics majors taking Mathematics of the Secondary School Curriculum scored 3’s. Of the 11 mathematics majors taking Mathematics of the Secondary School Curriculum, six scored at least one 3 on a scenario question. On a few questions, one to four of the 16 non-mathematics majors and one of the five mathematics majors not taking Mathematics of the Secondary School Curriculum scored 2’s; however, these students tended to score 1’s on most questions.
The score frequencies and topic mean scores indicated that respondents in this study sample scored lowest on the topic of quadratic function and highest on the topic of linear equation in two variables (see Table 5 and Table 6). This pattern was consistent for mathematics majors as well as non-mathematics majors. In particular, the first two questions on the quadratic function had the most 1’s: 15 of the 17 students (88%) who responded to these questions scored 1. Across the topics, the mathematics majors who were taking Mathematics of the Secondary School Curriculum on average had the highest topic mean score. Their average topic mean score ranged from 1.48 to 1.78 whereas the average topic mean score of the non-mathematics majors and the mathematics major who was not taking Mathematics of the Secondary School Curriculum ranged from 1 to 1.25.
The correlations of the raw scores indicated that participants’ responses to certain sets of scenario questions were correlated more than their responses to other scenario questions (see Table 7). The set of three dividing fractions questions were fairly correlated ![]() and the set of three quadratic function questions were strongly correlated
and the set of three quadratic function questions were strongly correlated ![]() whereas the set of four linear equation in two variables questions were less correlated
whereas the set of four linear equation in two variables questions were less correlated![]() . This means scores on the dividing fractions questions and the quadratic function questions were more consistent than scores on the linear equation questions. In other words, for a given student, his or her scores were generally high (or low) across all three dividing fractions questions or all three quadratic function questions whereas his or her scores generally varied more across the four linear equation questions. In addition, the correlations between the dividing fractions questions and the quadratic function questions were quite high
. This means scores on the dividing fractions questions and the quadratic function questions were more consistent than scores on the linear equation questions. In other words, for a given student, his or her scores were generally high (or low) across all three dividing fractions questions or all three quadratic function questions whereas his or her scores generally varied more across the four linear equation questions. In addition, the correlations between the dividing fractions questions and the quadratic function questions were quite high![]() , which resulted in the strong correlation between the topic mean scores
, which resulted in the strong correlation between the topic mean scores![]() , as shown in Table 8. This implies that students who scored high on dividing fractions questions generally tended to score high on quadratic function questions, and students who scored low on dividing fractions questions generally scored low on quadratic function questions. However, high scoring on the questions related to these two topics does not mean high scoring on the questions related to the linear equation topic.
, as shown in Table 8. This implies that students who scored high on dividing fractions questions generally tended to score high on quadratic function questions, and students who scored low on dividing fractions questions generally scored low on quadratic function questions. However, high scoring on the questions related to these two topics does not mean high scoring on the questions related to the linear equation topic.
![]()
Table 4. Distribution of students’ scores (N = 32).
![]()
Table 5. Score frequency (%) for each scenario question.
![]()
Table 6. Mean (standard deviation) for each topic.
![]()
Table 7. Correlations between scenario questions.
*p < 0.10; **p < 0.05; ***p < 0.01.
![]()
Table 8. Correlations between topic mean scores.
*p < 0.10; **p < 0.05; ***p < 0.01.
5.2. Characteristics of Students’ Responses
This section describes the variation and qualitative difference in students’ responses to demonstrate the characteristics of their content understanding on the three topics. Due to the page limit, we selected one scenario question from each of the three topics. The characterization of students’ responses to these three questions, however, can be generalized to other scenario questions.
5.2.1. What Does Dividing Fractions Mean?
No students scored 2 on questions 1.1 and 1.2. Responses that scored 3 show some characteristics of precision, coherence, and purposefulness whereas responses that scored 1lack these features. Consider the following response that scored 3:
Depending on their skill levels, it may take anywhere from 3 - 6 weeks to prepare them for this problem. I would ensure they understood that fundamentally, be it with whole numbers or fractions, addition is defined in the same way?by concatenating (laying side by side) line segments on the number line.
The respondent shows a deliberate effort at scaffolding mathematical ideas by showing students the connection between whole number and fraction operations. Beginning with addition, the respondent explains how the arithmetic operations are defined “in the same way” for whole numbers and fractions (by concatenating line segments on the number line). In this way, the respondent builds on students’ prior knowledge of whole numbers and extends those definitions to fractions. Furthermore, the respondent builds from simpler to more complex operations and shows the connection between multiplication and division:
After learning to add fractions, we can define multiplication of fractions: ![]() copies of the length obtained by splitting
copies of the length obtained by splitting ![]() into
into ![]() equal parts. We can then, from this definition, prove
equal parts. We can then, from this definition, prove![]() , which is
, which is
normally how fraction multiplication is defined. Finally, we define division the same way as for natural numbers:
![]() the unique number
the unique number ![]() s.t.
s.t.![]() . From here, we can show this definition implies “invert-and- multiply” rule ?
. From here, we can show this definition implies “invert-and- multiply” rule ?![]() . Notice up to this point, we have not used any “unusual” rules to help us manipulate fractions. Our definitions for the basic operations are essentially the same.
. Notice up to this point, we have not used any “unusual” rules to help us manipulate fractions. Our definitions for the basic operations are essentially the same.
Again, the respondent emphasizes how the definitions for the “basic” arithmetic operations are “essentially the same,” much like how the exemplary response refers to the “parallel logic” of dividing whole numbers and dividing fractions. Like the exemplary response, this respondent also approaches the given word problem by first posing it with integer measurements:
With this particular word problem, I would ensure they understood first a problem of the form “A rope 12 meters long is cut into 3 meter long pieces. How many of these pieces can we get out of the rope?” A more advanced mathematician would see immediately that this requires division, but sixth graders may not see that as quickly. A hands-on activity would be a good idea. When they begin to associate “splitting things into equal parts” with division, then a problem such as the above problem could be given to them. They would know the
answer is![]() , and from what they’ll learn regarding mixed # (part (2)), they would find this is
, and from what they’ll learn regarding mixed # (part (2)), they would find this is![]() .
.
Although the respondent recognizes that a sixth grader might not “see immediately that this requires division”, the respondent does not provide a rationale for why or how students would learn to “associate ‘splitting things into equal parts’ with division”. Unlike the exemplary response, this respondent does not utilize the definitions presented earlier in the response as a basis for the logical reasoning behind why this problem should involve division. Also absent in this response is the interconnectedness of mathematical ideas between the algebraic and the geometric representations of dividing numbers. Nevertheless, the respondent does demonstrate understanding of the logical progression of mathematical concepts (e.g., whole numbers to fractions; addition/subtraction to multiplication to division) and shows attention to scaffolding mathematical ideas for students (e.g., from simple to complex). The respondent also shows some effort of attending to some key mathematical ideas (e.g., common definitions for arithmetic operations of whole numbers and fractions).
Responses that scored 1, on the other hand, lacked the characteristics of precision, coherence, and purposefulness. For example, the following response makes an initial attempt at scaffolding mathematical ideas by posing the given word problem with integer measurements but does not follow through with any explanation of what division of whole numbers means or why it makes sense to divide the integers in the modified problem:
I would ask students to reword the problem. We would instead write the following: “A rope [?] meters long is cut into pieces which are each á?ñ meters long. How many such pieces can we get out of the rope?” We can see that in this problem if [?] and á?ñ were whole numbers (like 2 and 1, respectively) we would do the following calculations (CONCEPTUALLY):
![]()
Using this image and explanation, I hope it will provide an insightful pictorial representation of why we solve the problem this way”.
Without providing any definitions of multiplication or division, the respondent jumps to setting up “calculations”. Moreover, what started as a simple division of whole numbers problem was “conceptually” interpreted as
multiplication of fractions![]() , which shows no regard for the logical progression of ma-
, which shows no regard for the logical progression of ma-
thematical concepts. The respondent refers to “insightful pictorial representations” but none are presented in the response.
Many responses that scored 1 make no attempt to invoke students’ prior knowledge and familiarity with whole numbers or to offer any explanation of what division of fractions means and why it applies to the given word problem. Consider the following response:
“(1) As with any word problem, it is important to understand what is involved. As such, I would have students
draw a representative rope on their paper and section off some number of pieces which are ![]() meters long. For example: [picture of rope with the first
meters long. For example: [picture of rope with the first ![]() meters long sections marked] This builds the students’ visuali-
meters long sections marked] This builds the students’ visuali-
zation skills.
(2) Next, I ask students to identify “important” information in the question by circling all the numbers (i.e., ![]() ,
,![]() ). This builds word problem strategies.
). This builds word problem strategies.
(3) I then review how to change mixed #’s into improper fractions (i.e.,![]() ) since
) since ![]() .
.
(4) Then I ask students what does it mean to “cut something into pieces” and what operation ![]() do you associate with this cutting process. This will get students to think about division
do you associate with this cutting process. This will get students to think about division![]() .
.
Although the respondent begins by offering a geometric representation, the respondent does not connect this to the definition of dividing fractions. Instead, the respondent expects students to “associate” the “cutting process” with an “operation”. This approach is reflective of the common “key word” strategy that students are often taught to solve word problems (e.g., “‘more’ means addition”). Rather than helping students to build an understanding of what an arithmetic operation means, students are taught to “associate” the operation with a “process” or key word.
Responses that scored 1 also show lack of attention to key mathematical ideas. The respondents focus on outlining procedures to solve the problem rather than emphasizing the key ideas such as the definitions of whole numbers and fractions. Such responses suggest limited understanding of the purposefulness behind the topic of dividing fractions.
As these examples show, responses that scored 1 tend to focus on knowledge at the surface or mechanical level. Explanations are often vague, fragmented, or inaccurate. Overall, the responses lack precision, coherence, and purposefulness.
5.2.2. What Is the Connection among Different Forms of Linear Equations?
The one response that scored 3 on question 2.4 begins with a key mathematical idea, i.e., the definition of the graph of a linear equation:
We first define the graph of a linear eqn. as![]() . This immediately joins the first and last
. This immediately joins the first and last
concepts. Motivating the “standard form” of a linear equation in two variables is the fact that linear implies each term contains no more than one variable, so we can combine all the x terms into ax and the y terms into by, and all the constants into c. To translate this into slope-intercept, we notice that m is undefined when b = 0,
since a vertical line has an undefined slope. Therefore, we assume b ≠ 0. Then![]() , so
, so![]() . We let
. We let![]() . Notice that
. Notice that ![]() makes sense, since we have. But
makes sense, since we have. But ![]() for
for![]() , so
, so![]() .Therefore,
.Therefore,![]() . But the point-slope form falls out very naturally from this ?
. But the point-slope form falls out very naturally from this ?![]() gives us that
gives us that![]() , where
, where![]() . After factoring out
. After factoring out ![]() and bringing
and bringing ![]() to the left side, we have
to the left side, we have![]() .
.
The respondent emphasizes the connection between the different forms by using definitions and logical reasoning. The standard form and the graph are connected by definition (We first define the graph of a linear eqn.
as![]() ), and the other forms are connected by algebraic manipulation. But the respondent is careful not to assume that the coefficient of the x-term in the slope-intercept form,
), and the other forms are connected by algebraic manipulation. But the respondent is careful not to assume that the coefficient of the x-term in the slope-intercept form, ![]() , is the slope, as is commonly practiced in school mathematics textbooks. Instead, he justifies this by using the definition of the graph of a linear equation (
, is the slope, as is commonly practiced in school mathematics textbooks. Instead, he justifies this by using the definition of the graph of a linear equation (![]() implies
implies ![]() for
for![]() ) and the key fact about slope (
) and the key fact about slope (![]() where
where![]() ). Similarly, the respondent connects the point-slope form to the
). Similarly, the respondent connects the point-slope form to the
slope-intercept form by using the definition of the graph of a linear equation again, although less explicitly (implicit is the fact that ![]() so that
so that ![]() and
and ![]() leads to
leads to![]() ). Thus, we see the respondent purposefully uses definitions as a basis for logical reasoning and makes meaningful connections across key mathematical ideas.
). Thus, we see the respondent purposefully uses definitions as a basis for logical reasoning and makes meaningful connections across key mathematical ideas.
Like the exemplary response, this respondent recognizes the flexibility in the representation of a linear equation as a key idea that comes from the connections among the forms:
The moral of the story is that given any form of the linear equation in two variables, you can move into any other form, so long as you rename some constants and move the right terms around. Since they are equivalent, students can mix and match.
However, in contrast to the exemplary response, the respondent does not make explicit the connections between the algebraic and geometric representations of linear equations nor does the respondent highlight the utility of each form of the linear equation. The respondent states that “students can mix and match” the forms but does not discuss what unique information is provided by each form or how certain pieces of information about a (non-vertical) line can be used to write the corresponding linear equation in any one of these forms. Also absent is the effort to scaffold student understanding from concrete examples to the general forms of equations with symbols. Nevertheless, this response that scored a 3 emphasizes some of the key mathematical ideas and provides thorough reasoning based on precise definitions.
Responses that scored 2, on the other hand, either mention some key ideas but present incomplete reasoning or show an attempt to connect different forms of linear equation but miss the key ideas. Consider the following example:
First, I remind students that any two distinct points can generate a line and any line can be represented by a linear equation in two variables. As such, we can deduce a number of characteristics from a linear equation that represents a line. For example, we can deduce the x-intercept, y-intercept, slope, and points from an equation.
Next, I explain why there are different forms of the same equation by examining each form individually. For example, the point slope form ![]() is a linear equation and, from just looking at it, we know the line has slope
is a linear equation and, from just looking at it, we know the line has slope ![]() and point
and point![]() . Thus, it is called point-slope form! (I will give the analogy: each form is like a note to a mystery and each note gives us clues about this mystery. The point-slope form conveniently gives us 2 important clues/details about our line (i.e., point and slope) just by looking at the equation.)
. Thus, it is called point-slope form! (I will give the analogy: each form is like a note to a mystery and each note gives us clues about this mystery. The point-slope form conveniently gives us 2 important clues/details about our line (i.e., point and slope) just by looking at the equation.)
This respondent recognizes some of the key mathematical ideas (any line can be represented by a linear equation in two variables) and points out the useful information that each form of a linear equation provides about the line (the point-slope form conveniently gives us 2 important clues/details about our line (i.e., point and slope) just by looking at the equation). However, what is notably missing in this response is the logical reasoning. The respondent states, “from just looking at it (the point slope form![]() ), we know the line has slope
), we know the line has slope ![]() and point
and point![]() .” Yet, how does one know that the
.” Yet, how does one know that the ![]() represents the slope and that
represents the slope and that ![]() represent the x and y-coordinates, respectively, of a point on the line that corresponds to the given linear equation? Whereas the response that scored 3 justifies every assertion made, this response provides no reasoning or justification for why the point-slope form “conveniently gives us” a point on the line and the slope of the line. Moreover, there is no discussion of whether one can go from one form of the linear equation to another. The respondent claims, “all these forms of a linear equation allow us to graph our line, since they tell us the line’s characteristics (slope, point, x-intercept, etc.”; however, there is no explanation of how or why the different forms can provide such information about the same linear equation. In short, the response emphasizes some key mathematical ideas but does not support them with logical reasoning.
represent the x and y-coordinates, respectively, of a point on the line that corresponds to the given linear equation? Whereas the response that scored 3 justifies every assertion made, this response provides no reasoning or justification for why the point-slope form “conveniently gives us” a point on the line and the slope of the line. Moreover, there is no discussion of whether one can go from one form of the linear equation to another. The respondent claims, “all these forms of a linear equation allow us to graph our line, since they tell us the line’s characteristics (slope, point, x-intercept, etc.”; however, there is no explanation of how or why the different forms can provide such information about the same linear equation. In short, the response emphasizes some key mathematical ideas but does not support them with logical reasoning.
In contrast, the following example shows how each form can be rewritten into another form by algebraic manipulation but it does not point out key ideas that underlie different forms of a linear equation:
The forms![]() ,
,![]() , and
, and ![]() is pretty much the same thing. You can rearrange one form to make it look like the other. The only variables that matter is x and y.
is pretty much the same thing. You can rearrange one form to make it look like the other. The only variables that matter is x and y.
For example, ![]() can be converted to slope-intercept form
can be converted to slope-intercept form
![]()
![]()
In this case ![]() and
and![]() .
.
From this form, you can easily graph a linear equation with ![]() as slope and
as slope and ![]() as y-intercept.
as y-intercept.
The point-slope form ![]() can also be rearranged to slope-intercept form as well.
can also be rearranged to slope-intercept form as well.
![]()
where ![]()
On the one hand, the respondent clearly demonstrates how a linear equation in standard or point-slope form
can be written in slope-intercept form. On the other hand, there is no explanation of why ![]() is the slope or why
is the slope or why ![]() is the y-intercept of the line or any discussion of
is the y-intercept of the line or any discussion of![]() ’s geometric representations. There is no
’s geometric representations. There is no
effort to help students understand the reasoning behind the key ideas that connect a linear equation in two variables and its graph. Instead, the respondent simply states, “you can easily graph a linear equation with ![]() as slope and
as slope and ![]() as y-intercept” without using any definition or connection between linear equations and their graphs.
as y-intercept” without using any definition or connection between linear equations and their graphs.
This respondent’s approach to connecting the different forms of linear equations in two variables is representative of many responses that scored 1 or 2. In most cases, the standard form and point-slope form are shown to be equivalent to the slope-intercept form by algebraic manipulation (although some scores of 1 had errors in the algebraic manipulation). Whereas the exemplary response and the response that scored 3 both recognize the standard form ![]() as the most general form of linear equation and the exemplary response also notes the slope-intercept form as a special case of the standard form, responses that scored 1 or 2 emphasize the slope-intercept form as if that is the most general form of the linear equation. However, what these respondents overlook is that the slope-intercept form (as well as the point-slope form) only makes sense for non-vertical lines. They implicitly assume that the slope and y-intercept exist for every line and every graph of a linear equation.
as the most general form of linear equation and the exemplary response also notes the slope-intercept form as a special case of the standard form, responses that scored 1 or 2 emphasize the slope-intercept form as if that is the most general form of the linear equation. However, what these respondents overlook is that the slope-intercept form (as well as the point-slope form) only makes sense for non-vertical lines. They implicitly assume that the slope and y-intercept exist for every line and every graph of a linear equation.
Because of limited space, responses that scored 1 will not be further discussed. However, as these examples show, the responses of the study sample generally exhibit significantly less precision, coherence, and purposefulness than the exemplary response. Although the response that scored 3 uses definition as a basis for logical reasoning and connects some of the key mathematical ideas, all of the other responses lack at least one of the essential components that exemplify content understanding for teaching.
5.2.3. Why Do We Need Different forms of Quadratic Function?
Responses that scored 3 on questions 3.3 and 3.4 exhibit characteristics of coherence and purposefulness. Consider the following example:
Each of the forms emphasizes a certain property:
![]() shows that the quadratic function is like any other polynomial. It highlights the fact that although the quadratic is special, it belongs to a much larger, more general class of functions.
shows that the quadratic function is like any other polynomial. It highlights the fact that although the quadratic is special, it belongs to a much larger, more general class of functions.
![]() emphasizes the position of the vertex and the general shape of the quadratic. This form makes visualizing the graph of the quadratic easy, which is why it is normally used to graph quadratics.
emphasizes the position of the vertex and the general shape of the quadratic. This form makes visualizing the graph of the quadratic easy, which is why it is normally used to graph quadratics.
![]() gives a factorization of the quadratic. This form can be used to read off the roots directly as opposed to the other forms, where one needs to do some work to come up with the roots.
gives a factorization of the quadratic. This form can be used to read off the roots directly as opposed to the other forms, where one needs to do some work to come up with the roots.
The respondent points out the strengths and weaknesses of each form (![]() shows that the quadratic function is like any other polynomial whereas
shows that the quadratic function is like any other polynomial whereas ![]() can be used to read off the roots directly) and makes explicit the connections between the algebraic and geometric representations of the quadratic function (
can be used to read off the roots directly) and makes explicit the connections between the algebraic and geometric representations of the quadratic function (![]() emphasizes the position of the vertex and the general shape of the quadratic). In addition, the respondent recognizes the coherent structure of mathematics wherein the quadratic function is one member of a larger family of polynomial functions (i.e.,
emphasizes the position of the vertex and the general shape of the quadratic). In addition, the respondent recognizes the coherent structure of mathematics wherein the quadratic function is one member of a larger family of polynomial functions (i.e., ![]() highlights the fact that although the quadratic is special, it belongs to a much larger, more general class of functions). The response to this scenario question, however, does not show a logical progression from concrete examples to general cases. Furthermore, the respondent does not display an effort at explicitly connecting students’ prior knowledge with the mathematical ideas embedded in the present context.
highlights the fact that although the quadratic is special, it belongs to a much larger, more general class of functions). The response to this scenario question, however, does not show a logical progression from concrete examples to general cases. Furthermore, the respondent does not display an effort at explicitly connecting students’ prior knowledge with the mathematical ideas embedded in the present context.
Responses that scored 2 also make connections between the algebraic and geometric representations of the quadratic function but fail to recognize the purpose of the standard form:
Each of the forms shows a different way to write the same equation. We change the equation to a different form to collect information about the equation and graph it easier.
When the equation is in the form ![]() it is hard to determine the x-intercepts by just looking at the equation. But if we change it to the form,
it is hard to determine the x-intercepts by just looking at the equation. But if we change it to the form, ![]() it is easy to determine the x-intercepts, which are
it is easy to determine the x-intercepts, which are![]() .
.
Similarly, if the equation is of the form![]() , it would be difficult to determine the vertex of the equation, but if the equation is of the form
, it would be difficult to determine the vertex of the equation, but if the equation is of the form ![]() then it is easy to see the vertex of the equation.
then it is easy to see the vertex of the equation.
Acquiring this information would make graphing sketches of the equation faster and easier.
Whereas responses that scored 2 make clear connections between the algebraic and geometric representations of the quadratic function, responses that scored 1 are not as specific or thorough:
It might be clearer in different forms looking for different answers, i.e., what are the zeroes, what are the x and y intercepts?
As the examples in this section show, responses to this scenario question display varied levels of detail and thoroughness in describing the purpose of each form of the quadratic function and the connection between the algebraic and geometric representations of the quadratic function. However, absent in nearly all of the responses is an effort to emphasize the logical progression of mathematical concepts and scaffold mathematical ideas for students in a systematic and coherent way, from simple to complex and from specific to general.
To summarize, we have described in this section how the responses in our study sample vary qualitatively. In general, they do not exemplify precision, coherence, and purposefulness to the extent that the exemplary response does. Attempts to emphasize the key mathematical idea, its rationale, the logical progression of mathematical concepts, and the connectedness among different mathematical concepts, procedures, and ideas are fairly consistent among the highest scoring respondents but notably absent among the lowest scoring respondents. Attention to scaffolding ideas in a systematic and coherent way is present in some responses that scored 3 but missing in responses that scored 1 or 2. These responses indicate a wide range of understandings of the three key early algebra topics among the sampled students in our study, but none have reached the exemplary level of understanding (i.e., scoring 4 on the rubric).
6. Summary and Discussion
Subject matter knowledge plays a central role in teaching ( Ball, Hill, & Bass, 2005; Buchmann, 1984). One common assumption is that having a major in STEM is equivalent to being able to teach that content at the K-12 level. In other words, a college major in mathematics is used to signal a candidate’s content knowledge for teaching K-12 students, assuming that math majors have the deep understanding of the K-12 topics to teach well at that level. This assumption is manifested to some extent in the recent efforts at recruiting undergraduate STEM majors into teaching through programs such as 100k10 in New York, UTeach in Texas, and UTeach replication sites across the country.
What has not been brought to the forefront is the fact that the content focus on typical college mathematics courses serves a different purpose from content needed for teaching at the K-12 level (Wu, 2011a) . It is therefore of critical importance to examine the nature of mathematical knowledge that is needed for teaching mathematics at the K-12 level. There is at present little research on the kinds of mathematical knowledge that teachers need to have in order to effectively prepare students for learning high school algebra. Through this study, we hope to make a contribution to fill this gap in two ways.
First, our study describes what exemplary understandings of the three key early algebra topics look like and outlines key attributes that characterize such understandings. As can be seen in the examples, they exemplify precision, coherence, and purposefulness. There is consistent and substantial evidence of an attempt to emphasize the key mathematical idea, its rationale, the logical progression of mathematical concepts, and the connectedness among different mathematical concepts, procedures, and ideas. In addition, these responses pay a deliberate attention to scaffolding mathematical ideas to students in a systematic and coherent way, from simple to complex and from specific to general.
A second contribution of our study is to examine mathematical content understanding for teaching K-12 among the sample of STEM majors in our study, because it is typically assumed that college majors are equivalent to having solid content knowledge for teaching at the K-12 level (Ball, 1990) . The finding from our study shows that STEM majors in our study sample do not possess the deep understanding of the three topics we investigated. Specifically, among the 32 study participants, most of them scored 1’s across the scenario questions while others mostly scored 1’s or 2’s. A small number of participants scored 3 on some scenario questions. This suggests that even though these STEM majors might be strong in their disciplinary knowledge, they do not necessarily have the depth of understanding of K-12 topics in order to teach at that level.
Furthermore, the small number of participants who scored 3’s on some of the scenario questions are math majors who were taking Mathematics of the Secondary School Curriculum, a 3-semester course sequence designed to teach grades 6-12 content for math majors interested in pursuing teaching as a career. Non-math majors or math majors who were not taking Mathematics of the Secondary School Curriculum mostly scored 1’s or 1’s and 2’s and none scored 3’s on any of the scenario questions. These results signal the importance of explicitly teaching future math teachers the content knowledge that they will be teaching to their students down the road.
In addition to these quantitative results, qualitative analysis of the characteristics of content understanding for teaching among the study participants shows that in general, their understanding do not exemplify precision, coherence, and purposefulness. In other words, their levels of understanding do not meet the standards for teaching at that level. In addition, there is variation in their understanding among the study participants. In particular, attempts to emphasize the key mathematical idea, its rationale, the logical progression of mathematical concepts, and the connectedness among different mathematical concepts, procedures, and ideas are fairly consistent among the highest scoring respondents (i.e., those scored 3’s) but notably absent among the lowest scoring respondents (those scored 1’s). Furthermore, attention to scaffolding ideas in a systematic and coherent way is present in some responses that scored 3’s but missing in responses that scored 1’s or 2’s.
Taken together, these findings have important implications for the content training of future math teachers in order to increase the quality of the teaching force in terms of their content preparation. Though efforts at recruiting undergraduate STEM majors to improve the quality of the teaching force in mathematics are commendable, we need to provide recruits with explicit content training of mathematics topics that they are expected to teach at the K-12 level. Otherwise, STEM majors will resort to the way they were taught as K-12 students when they become teachers one day. For example, the UC Berkeley math department is one of the few that offer math content courses specifically focusing on grades 6-12 content for math majors who are interested in pursuing teaching as a career. We need policies that promote college math departments’ involvement in the training of future math teachers.
In addition, our findings have implications for using teachers’ college math coursework as a proxy measure of math teachers’ content knowledge as many empirical studies have done. As pointed out previously, empirical studies on the relationship between teachers’ college math coursework and their students’ mathematical performance have yielded mixed results. One possible explanation might be that having advanced mathematical knowledge at college level does not necessarily equate having deep understanding of K-12 content, which is necessary in order to translate this deep understanding into effective classroom practices in terms of engaging K- 12 students around substantive mathematics. Therefore, instead of using proxy measures such as college math coursework, directly measuring math teachers’ understanding of K-12 content they teach may help to produce consistent results on the relationship between teacher mathematical knowledge and students’ achievement.
Finally, our study findings have implications for the professional development of in-service teachers. Since most teachers did not have the opportunities to learn the content knowledge they need to teach from their college math courses, they typically resort to the way they were taught as K-12 students (Adams & Krockover, 1997; Lortie, 1975) . To improve the quality of teachers’ content understanding, we need in-service professional development activities that focus explicitly on the content knowledge they are teaching.
By outlining and investigating the nature of mathematical knowledge future teachers need in order to teach K- 12 students, we hope information generated from the study is relevant for a variety of stakeholder groups, including policy makers who are concerned with the quality of students’ mathematical learning, K-16 educators and administrators who are concerned with students’ under-preparation in quantitative skills for college and work, scholars whose research focuses on issues related to K-12 mathematics education and the STEM labor market, curricular developers who are interested in designing intervention materials for struggling mathematics students, and the general public who is interested in mathematics educational issues.
Acknowledgements
We would like to thank professors Hung-Hsi Wu (Department of Mathematics) and Alan Schoenfeld (Graduate School of Education), both at University of California, Berkeley, and professor Jeff Shih (Department of Teaching and Learning) at University of Nevada, Las Vegas for their comments on earlier drafts of the paper. In addition, we would like to thank anonymous reviewers for their constructive feedback. Last but not least, we would also like to thank the Cal Teach faculty and the Berkeley Science and Math Initiative research group for their support of this study. Opinions reflect those of the authors.
Appendix A Linear Equations in Two Variables and Their Graphs
What is the assumption or key mathematical concept underlying proportionality mathematics problems? Proportionality occupies a significant role in algebra because it is used to teach students how to solve word problems dealing with speed, rate, and so on. One important amiss, however, lies in the fact that students are never taught about the key mathematical idea underlying such problems, i.e., making explicit the assumption we make in order to solve proportionality mathematics problems. We used scenario questions 2.1 and 2.2 to probe participants’ awareness of this issue. Since question 2.2 asks respondents to come up with a story, an exemplary response is one that is explicit about the underlying assumption needed to solve the problem. The discussion here focuses on question 2.1. Below is an exemplary response to this question:
The people who wrote this problem made an assumption. Can you see what it was? They assumed that Abe runs at a constant speed. Does that help you solve the problem?
“Einstein” might only need this much information. But he might need more, in which case the teacher might continue as follows:
So what does running at a constant speed mean? First, I would ask students how we calculate the average speed for Abe, which is:
Average speed ran during any time interval from t1 to t2 = ![]()
To say that Abe is running at a constant speed, by definition, means that the average speed for any time interval is a constant (or fixed) number, which we’ll call “v”.
Note the respondent immediately focuses on the key idea (i.e., the key to solving this problem is to assume that Abe runs at a constant speed). Then the respondent continues the line of reasoning by asking for the meaning of “running at a constant speed”. To do this, the respondent invokes a related idea, i.e., average speed, because this concept is the basis for defining constant speed (i.e., “To say that Abe is running at a constant speed, by definition, means that the average speed for any time interval is a constant (or fixed) number”). Here the respondent is very deliberate about using the definition as a basis for helping students “see” what reasoning makes it possible to set up proportionality problems, as shown below:
“Let D1 be the distance traveled from time = 0 to t1 and D2 be the distance traveled from time = 0 to t2. Then:
![]()
By the definition of division, this is equivalent to
![]()
Let t represent time (t > 0) and D represent the distance traveled from time = 0 to t. Then we can rewrite the above equation as:
![]()
Furthermore, if we consider the time interval 0 to any time t, we get:
![]()
This is a linear equation in two variables, t and D, without the constant term. It’s important to see that the key idea used to arrive at this equation is the definition of constant speed.
Building on the definition of constant speed, the respondent uses definition again (i.e., definition of division) to re-write the equation into a form that helps them to connect the definition of constant speed and linear equations in two variables without the constant term. This is the basis for the so-called proportionality reasoning that is used to solve a wide variety of problems involving speed, rate, etc.
Finally, the respondent is keenly aware of how what they are learning at the 8th grade might be connected with the mathematical concept they will learn later, i.e., function.
[Note: Later when students are introduced to the linear function, I’d also help them make the connection that the underlying mathematical concept for problems of constant speed or rate is a linear function in one variable without the constant term.]
Overall, the respondent is very purposeful in his or her reasoning and shows deliberate effort at using definition as a basis for logical reasoning and making explicit the interconnectedness of mathematical ideas at different levels of complexity.
Why can the slope of a line be calculated using any two distinct points on the line? Slope features prominently when teaching linear equations in the K-12 curriculum. Much of the emphasis in the textbook focuses more on the mechanic calculation than on the conceptual understanding of the concept of slope or the connection between linear equation and its graph. We used scenario question 2.3 to investigate respondents’ understanding of the concept of slope and the connection between linear equation and its graph.
An exemplary response to this scenario question begins with the definition of the slope of a line:
The key mathematical idea underlying this question is that the slope of a line can be calculated using any two points on the line (i.e., independence of any two distinct points on the line). So how can we help students learn this key idea? Before I use P1, P2, P3, P4 as shown in the picture, I would first review with students how the slope of a line is defined: given a line and assuming it slants upward (as the picture shows), let’s take a point P on the line, go 1 unit horizontally to point R, then go upward (or vertically) and let the vertical line from R intersect the given line at point Q. Then the definition of slope is the length of segment QR (i.e., |QR|).
![]()
Here the respondent is laying a foundation for what comes next by precisely defining the slope of a line and showing this on the graph. Note how the respondent expands the definition and stretches students’ thinking by posing the next question:
But how are we certain that this vertical length |QR| is the same for any point P we choose on the line? In other words: if we take another point P' on the line, go 1 unit horizontally to point R’ and then go upward to intersect the line at point Q', how do we know that![]() )?
)?
![]()
To answer this question, students need to invoke their knowledge of similar triangle. This is an important step towards defining the slope precisely and completely, as the respondent points out:
I would expect the following explanation from students: ![]() (corresponding angles on parallel lines) and
(corresponding angles on parallel lines) and![]() , so by the angle-angle-side criterion,
, so by the angle-angle-side criterion, ![]() and, thus,
and, thus,![]() . Therefore, the slope is independent of the point P and it makes sense to talk about the slope of the line.
. Therefore, the slope is independent of the point P and it makes sense to talk about the slope of the line.
With the definition complete, the respondent adds complexity by posing the following question: “Can we find another, more flexible way of finding the slope of a line, without having to measure 1 unit horizontally from a point on the line and then the vertical distance up?”This step builds on the previous step of defining the slope of the line but uses similar ideas (i.e., similar triangle), as shown below:
To answer this question, let’s do the following: let P, Q, R be as before (i.e., P is any point on the line used to define the slope of the line) and now suppose we take any other point on the line, call it S. From S, draw a vertical line and let it meet the horizontal line PR at point T.
![]()
So now look at the two triangles, ∆PQR and ∆PST. What can we say about them? Hopefully students would recognize that they are similar triangles; if not, I’d tell them but ask them to prove (explain) why the triangles are similar (by the angle-angle criterion: right angles formed by perpendicular lines and corresponding angles on parallel lines).
After establishing the fact that![]() , I would then ask: what can we say about the relationship between the sides of the triangles? One of the things I would expect students to mention would be:
, I would then ask: what can we say about the relationship between the sides of the triangles? One of the things I would expect students to mention would be:
![]()
Then I would guide them to manipulate the above equation into the following:
![]()
At this point, I would ask students what they observe. Hopefully they would recognize that, since |PR| = 1, the left side of the equation is equal to line segment |QR|, which is the slope of the line. In other words:
![]()
Of course, the respondent is very purposeful about why they are doing this exercise:
From this exercise, I would hope students reached the following conclusions:
1. The slope of the line can be calculated using points P (the point we used to define the slope) and S (any other point on the line).
2. We can calculate the slope of a line by dividing the length of the vertical line segment by the length of the horizontal line segment of![]() .
.
Because we had shown earlier that the point P used to define the slope is arbitrary (i.e., can be any point on the line) and we had defined S to be another arbitrary point on the line, then the conclusions above can be generalized into the following:
1. The slope of the line can be calculated using any two distinct points, P and S, on the line.
2. We can calculate the slope of a line by dividing the length of the vertical line segment by the length of the horizontal line segment of![]() .
.
This purposefulness brings mathematical closure to students and we see how the respondent is very deliberate in scaffolding key ideas throughout the process. Having shown the underlying key ideas, the respondent then goes back to the original question (i.e., using P1, P2, P3, and P4) and has students work out the proof on their own:
To reinforce these main ideas, I would have students work in groups or pairs to prove (using similar triangle properties) that the slope of the line calculated by P1, P2 (in the original graph above) is the same as the slope calculated by P3, P4. Once they finish working in groups, I’d have a whole-class discussion and ask students to show how they did the proof. Below is an example of what I’d expect:
Draw in the horizontal and vertical lines through points P1, P2, P3, P4 and let them intersect at points Q and R as shown below:
![]()
We claim that the two triangles formed, DP1P2Q and DP3P4R, are similar. The reason is: |ÐP1QP2| = |ÐP3RP4| because both equal 90˚ and |ÐP1P2Q| = |ÐP3P4R| because they are corresponding angles on parallel lines. Then, by the angle-angle criterion, DP1P2Q ~ DP3P4R. By the key triangle similarity theorem, we can then
say![]() , and by multiplying both sides of the equation by
, and by multiplying both sides of the equation by ![]() and
and![]() , we get
, we get![]() .
.
That means the slope calculated by P1, P2 is the same as the slope calculated by P3,P4. Therefore, the slope can be calculated by any two distinct points on the line.
Looking at this exemplary response overall, we see that the respondent is mindful of the purpose of each activity, focuses on the key ideas and scaffold these key ideas in a coherent way, starting with the definition, using it as a basis for subsequent logical reasoning, and leading students from simple ideas to more complex ones, from specific examples to general cases.
What is the connection among different forms of linear equations? A routine exercise students in early algebra classes do is to memorize different forms of linear equations (e.g., standard form, point-slope form, two-point form, intercept-slope form, etc.). This rote learning deprives students the opportunity to understand the connections among different forms of linear equations. For instance, students trained in rote learning are not given the opportunities to ponder the following questions: why can a linear equation be written in different forms? What information is given in each form of the same linear equation? What is the connection among different forms? Can one go from one form to another? Knowing the answers to these questions will deepen students’ understanding of linear equations. We used scenario question 2.4 to examine study participants’ understanding of these questions.
The exemplary response to the scenario question used to examine study participants’ understanding of these questions is purposeful and focuses on the key mathematical ideas, as shown below:
The key idea is that students should not need to memorize different forms of linear equations (so that they mechanically match a particular given piece of information with a particular form). The key is to understand the connection between a linear equation in two variables and its graph, so that students can use any given information to figure out the eqation of a line; or vice versa, given an equation, the students should know what its graph looks like.
To help students understand these key ideas, the respondent again resorts to using definition as a basis for logical reasoning:
The following ideas are central to understanding the connection between a linear equation in two variables and its graph. So before addressing the question raised in the scenario, I’d want students to know the following facts:
- Definition of the graph of a linear equation: collection of all ordered pairs (x0, y0) that satisfy the equation ![]() (where a ¹ 0 or b ¹ 0).
(where a ¹ 0 or b ¹ 0).
- The graph of a linear equation is a straight line; every straight line is the graph of some linear equation. [This is something that can be proved; though I might not do the proof with students right away, I’d at least point this out so that students know it can be proved.]
- The slope of a line can be calculated using any two distinct points on the line.
Having laid this foundation, the respondent begins a carefully orchestrated process of leading students to discover the key mathematical ideas:
With these basic understandings about a linear equation in two variables and its graph, I would first ask students to graph, by hand, the line![]() . Then I’d ask them to work in groups or pairs to:
. Then I’d ask them to work in groups or pairs to:
- Calculate the slope and the y-intercept (i.e., when x = 0)
- Show on the graph where/what is: slope and y-intercept
The purpose for this exercise is to get students to feel comfortable connecting algebraic calculations and graphical representations, especially as they relate to the slope and y-intercept.
Note the respondent begins with a concrete example and is very deliberate about the purpose behind this exercise: preparing students for what comes next:
Then I’d give students a line (say it’s the graph of![]() , just to make it easier), and ask them to figure out what the equation for the line is, if:
, just to make it easier), and ask them to figure out what the equation for the line is, if:
1) We know one point and the slope
2) We know two points
3) We know the y-intercept and slope
The specific steps may go something like this:
(1) Given slope and a point:
Teacher prompt:
Suppose the slope of a line is 3 and a point on the line is![]() . What's the equation of the line?
. What's the equation of the line?
Expected student response:
We’ve learned that the slope of a line can be calculated by using any two distinct points on the line. We know one point is given:![]() . Let
. Let ![]() be any other point on the line. Then the slope is
be any other point on the line. Then the slope is![]() . But we’re also given that the slope is 3, so
. But we’re also given that the slope is 3, so![]() . By the definition of division, we get
. By the definition of division, we get ![]() .
.
[The interim step, ![]() , will be used later when I show them the generic point-slope form
, will be used later when I show them the generic point-slope form ![]() and have students compare this step to the generic slope-intercept form.]
and have students compare this step to the generic slope-intercept form.]
(2) Given two points:
Teacher prompt:
Suppose a line contains points ![]() and
and![]() . What’s the equation of the line?
. What’s the equation of the line?
Expected student response:
Let ![]() be any other point on the line besides
be any other point on the line besides ![]() or
or![]() . Using the same reason as before (i.e., any two distinct points give the slope of the line), we get:
. Using the same reason as before (i.e., any two distinct points give the slope of the line), we get:
![]()
(3) Given slope and y-intercept:
Teacher prompt:
Suppose the slope of a line is 3 and the y-intercept of the line is −2. What’s the equation of the line?
[Recall the earlier task where students used the graph to connect the y-intercept to the y-coordinate of the point where the line intersects the y-axis. The point of intersection is ![]() where
where ![]() is the y-intercept of the line.]
is the y-intercept of the line.]
Expected student response:
We’ve learned that, because −2 is the y?intercept, then ![]() is a point on the line. Let
is a point on the line. Let ![]() be any other point on the line besides
be any other point on the line besides![]() . Using the same reason as before (i.e., any two distinct points give the slope of the line), we get:
. Using the same reason as before (i.e., any two distinct points give the slope of the line), we get:
![]()
[The alternative interim step, ![]() , will later be used to compare to the generic slope-intercept form,
, will later be used to compare to the generic slope-intercept form,![]() ].
].
The purpose of this exercise is to get students used to figuring out the equation when different pieces of information are given. I would forbid them to use the forms as given in the textbook; instead, I would ask students to figure out the equations based on their understandings of the definition of the graph of linear equation and the connection between linear equations and their graphs (listed at the start of this response).
Throughout these exercises, the respondent connects ideas that students have learned in the previous steps with what they are doing now. In addition, the respondent is purposeful about emphasizing key mathematical ideas and using definition as a basis for logical reasoning. The process of discovery is coherent, going from simple to complex and from specific to general:
Once students figured out the linear equations based on different pieces of given information, I’d ask them to arrange their equations in the forms as shown in the scenario questions (now I’d show them the forms which are popular in textbooks), compare their equations with the general cases (i.e., the symbols) and see what they think. For example, to get ![]() into the form
into the form![]() , students would add y and subtract 2 from both sides of the equation.
, students would add y and subtract 2 from both sides of the equation.
I would then talk about the significance of the constants in the forms ![]() and
and![]() . Students should easily recognize the first form from case (1) above: given a line with slope m and point
. Students should easily recognize the first form from case (1) above: given a line with slope m and point ![]() and letting
and letting ![]() be any other point on the line, we get:
be any other point on the line, we get:![]() . So, that’s why this form is called the point-slope form.
. So, that’s why this form is called the point-slope form.
When we consider the form![]() , students should easily see that the b is the y-intercept because y = b when x = 0. However, what is the constant m? (Note: we don’t know that the m in this form represents the same number m in the point-slope form above) To answer this question, we do the following:
, students should easily see that the b is the y-intercept because y = b when x = 0. However, what is the constant m? (Note: we don’t know that the m in this form represents the same number m in the point-slope form above) To answer this question, we do the following:
Say the equation of a line is: ![]() where m and b are constants. Let
where m and b are constants. Let ![]() and
and ![]() be two distinct points on the line. Because the two points are on the line, by definition,
be two distinct points on the line. Because the two points are on the line, by definition, ![]() and
and![]() . Then what is the slope of the line?
. Then what is the slope of the line?
![]()
Note that the final step is possible because![]() . Therefore, the m is the slope of the line, and that’s why
. Therefore, the m is the slope of the line, and that’s why ![]() is called the slope-intercept form.
is called the slope-intercept form.
Other things I’d look for in their understanding at this point:
- The standard form is the most general form. It includes cases when b=0 (i.e., vertical line), which cannot be represented in the other two forms. However, this form doesn’t immediately show the slope.
- The slope-intercept form is a special case of the standard form where b is restricted to 1. This form helps us immediately identify the slope of the line (and the y-intercept). Also, it’s the form used when we talk about linear functions.
The point-slope form is also a special case of the standard form where b is restricted to 1. In addition, the point-slope form is, in principle, essentially the same as the slope-intercept form because the information given to figure out the equation is the same (i.e., in both cases, the slope is given, plus one point on the line: in the slope-intercept form the point given is ![]() where b is the y-intercept; in the point slope form the point given is
where b is the y-intercept; in the point slope form the point given is![]() . Note that, in the latter case, if
. Note that, in the latter case, if![]() , then
, then ![]() is the point where the line intersects the y-axis. Therefore, it can be used to write the linear equation in slope-intercept form. Likewise, given the y-intercept, we can write the linear equation in point-slope form).
is the point where the line intersects the y-axis. Therefore, it can be used to write the linear equation in slope-intercept form. Likewise, given the y-intercept, we can write the linear equation in point-slope form).
Note the respondent helps students to connect the general forms of equations (i.e., using symbols) with the concrete examples they have worked on. Furthermore, instead of asking students to mindlessly memorize different forms of linear equations, the respondent emphasizes the connection between different forms and between the algebraic and geometric representations of linear equations. Throughout, we see the respondent is deliberate at using definition as a basis for logical reasoning, emphasizing and connecting key mathematical ideas, and scaffolding the reasoning process in a coherent way from simple to complex and from specific to general. Overall, the response is complete and characterized with precision, coherence, and purposefulness.
Appendix B Quadratic Functions and Their Graphs
Quadratic functions are significantly more complex, mathematically, than linear functions. However, the key to helping students learn this topic is for students to have a firm grasp of the graph of the quadratic function and its algebraic expression. Several central mathematical ideas are behind the scenario questions (see 3.1 to 3.4 in Table 2) on quadratic function and its graph, including: (1) Enable students to have comfort and familiarity with the graph of the quadratic function, through knowing the graph of the unit quadratic function![]() . This foundational understanding sets students on the path to understand, (a) how standard quadratic functions
. This foundational understanding sets students on the path to understand, (a) how standard quadratic functions ![]() relate to
relate to![]() ;that is, the graphs of
;that is, the graphs of ![]() are dilations of the graph of
are dilations of the graph of![]() . Or put it differently, the graphs of
. Or put it differently, the graphs of ![]() are similar to the graph of the unit quadratic function
are similar to the graph of the unit quadratic function![]() . In addition, it is important to help students understand, (b) that the graph of
. In addition, it is important to help students understand, (b) that the graph of ![]() is congruent to the graph of some standard quadratic function
is congruent to the graph of some standard quadratic function ![]() through translation. And combined (i.e., a and b), these two ideas help students understand that all the graphs of quadratic functions
through translation. And combined (i.e., a and b), these two ideas help students understand that all the graphs of quadratic functions ![]() are similar to each other; (2) Help students understand how to rewrite the standard form into the vertex and root forms, both graphically and algebraically (i.e., completing the square); and (3) Help students understand why the vertex and root forms are better than the standard polynomial form that is typically given. In other words, what information about the graph does each of these forms contain about the quadratic function? How does the quadratic formula fit in all of this? And what do we know about the connection between the roots of the quadratic function (if the discriminant is greater than or equal to zero) and the constants? Let’s see how these key ideas are scaffolded in the exemplary responses to the questions.
are similar to each other; (2) Help students understand how to rewrite the standard form into the vertex and root forms, both graphically and algebraically (i.e., completing the square); and (3) Help students understand why the vertex and root forms are better than the standard polynomial form that is typically given. In other words, what information about the graph does each of these forms contain about the quadratic function? How does the quadratic formula fit in all of this? And what do we know about the connection between the roots of the quadratic function (if the discriminant is greater than or equal to zero) and the constants? Let’s see how these key ideas are scaffolded in the exemplary responses to the questions.
The Graph of Quadratic Functions. Question 3.1 focuses onenabling students to have comfort and familiarity with the graph of the quadratic function, through knowing the graph of the unit quadratic function![]() .
.
As shown in the following response, the respondent is purposeful and emphasizes the key ideas underlying the mathematical activities:
The key idea I hope students would understand is that the graph of ![]() is similar to the graph of
is similar to the graph of ![]() through dilation and translation (and reflection if a < 0). But how do we get there? What kind of translation will take us from the graph of
through dilation and translation (and reflection if a < 0). But how do we get there? What kind of translation will take us from the graph of ![]() to the graph of
to the graph of ![]() (after
(after
transforming the graph of ![]() into the graph of
into the graph of ![]() through dilation by scale factor of
through dilation by scale factor of ![]() and centered at the origin)?
and centered at the origin)?
In addition, the respondent is very deliberate at using definition as a basis for logical reasoning:
I’d first help students understand that, for a point to be on the graph of a function ![]() (whether linear or quadratic), it means that the x-coordinate and y-coordinate of the point are connected through the given function in the following way:
(whether linear or quadratic), it means that the x-coordinate and y-coordinate of the point are connected through the given function in the following way:![]() . Furthermore, the graph of a function
. Furthermore, the graph of a function ![]() is the collection of all points of the form
is the collection of all points of the form![]() .
.
With this foundational understanding, the respondent shows a carefully thought-out guided practice to scaffold complex ideas through simple, concrete examples:
With this understanding, the first quadratic function we would consider is![]() . To help students graph
. To help students graph ![]() by hand, I would have them set up a table with the following x-values.
by hand, I would have them set up a table with the following x-values.
Then I would ask them: how do we find the points on the graph of g that have these x-values? I would expect students to recall the definition above and realize that they first need to calculate ![]() for each of the x-values listed.
for each of the x-values listed.
Then each point ![]() would be a point on the graph of g. Therefore, their graph of g would include the points (0, 0), (−1, 1), (1, 1), (2, 4), (−2, 4), (3, 9), (−3, 9).
would be a point on the graph of g. Therefore, their graph of g would include the points (0, 0), (−1, 1), (1, 1), (2, 4), (−2, 4), (3, 9), (−3, 9).
Once the students are familiarized and feel comfortable with this simple quadratic function, the respondent pushes their thinking further, again through a concrete example:
Then I’d say, now let’s look at how the graph changes when we change the coefficient of ![]() in the function
in the function![]() . First of all, what is the coefficient of
. First of all, what is the coefficient of ![]() in the unit quadratic
in the unit quadratic![]() ? [Answer = 1] That means, we want to look at graphs of
? [Answer = 1] That means, we want to look at graphs of ![]() where a is not 1 (or 0). Let’s first consider the case when a is positive, say 2. What will the graph of
where a is not 1 (or 0). Let’s first consider the case when a is positive, say 2. What will the graph of ![]() look like? I would expect students to suggest we use the same method as before and expand the table.
look like? I would expect students to suggest we use the same method as before and expand the table.
Then we would consider when a is negative, say −2. Again, we would expand the table.
As can be seen, the respondent is very deliberate in carefully scaffolding the complex ideas in a systematic and coherent way to the students. At the end of these activities, the respondent is very purposeful about bringing mathematical closure to the key concepts and ideas that students should acquire through these exercises:
After graphing ![]() and a few more cases, I’d have a class discussion along the line of: What happens to the graph when the coefficient of
and a few more cases, I’d have a class discussion along the line of: What happens to the graph when the coefficient of ![]() changes? And by extension (or generalization), what does the coefficient “a” do to the graph of g to get to the graph of
changes? And by extension (or generalization), what does the coefficient “a” do to the graph of g to get to the graph of![]() ? What happens when “a” is positive? What happens when “a” is negative? I would expect students to offer the following observations:
? What happens when “a” is positive? What happens when “a” is negative? I would expect students to offer the following observations:
When a is positive and greater than 1, the graph appears to keep the same shape as the graph of g but looks “thinner” than the graph of g.
When a is positive and between 0 and 1, the graph appears to keep the same shape as the graph of g but looks “wider” than the graph of g.
When a is negative, the graph appears to be the reflection across the y-axis of the cases above.
I would explain to students that describing the graph of ![]() as the “same shape” but “thinner” or “wider” than the graph of g means the graph of
as the “same shape” but “thinner” or “wider” than the graph of g means the graph of ![]() is similar to the graph of g. By definition of similarity, that means the graph of
is similar to the graph of g. By definition of similarity, that means the graph of ![]() is a dilation of the graph of g. I would have students confirm this fact with the following exercise (assuming students have had ample practice with dilations before this): dilate the points of g found earlier
is a dilation of the graph of g. I would have students confirm this fact with the following exercise (assuming students have had ample practice with dilations before this): dilate the points of g found earlier
by a scale factor ![]() and center at the origin (0, 0). Students should find that the dilated points coincide with the
and center at the origin (0, 0). Students should find that the dilated points coincide with the
points found earlier for the graph of ![]() and, therefore, this dilation transforms the graph of g to the graph of
and, therefore, this dilation transforms the graph of g to the graph of![]() .
.
Next, we see that the respondent extends students’ thinking by pushing them to work with general forms (i.e., use symbols) following the same logic they used with concrete examples. The respondent is very deliberate at demonstrating the interconnectedness of mathematical ideas and showing the logical progression of mathematical ideas:
Following the same logic as outlined above (i.e., how I’d help students understand the connection between g and ![]() when a ¹ 1 or 0), I’d systematically ask students to graph the following functions, by hand:
when a ¹ 1 or 0), I’d systematically ask students to graph the following functions, by hand:
- ![]()
First, set a = 2 and vary q (e.g., let q be 1, 2, −-1, −2). Next, set a = −2 and vary q in the same way. Then have a discussion on what “q” does to the graph: What happens when “q” is positive”? What happens when “q” is negative? I would want students to conclude that the q translates the graph of ![]() q units up when q > 0 and q units down when q < 0.
q units up when q > 0 and q units down when q < 0.
- ![]()
In the same manner, I’d set a = 2, q = 1 but vary p and have students graph each case. Then, I’d have a discussion on what “p” does to the graph. I would want students to conclude that the p translates the graph of h p units to the left when p < 0 and p units to the right when p > 0.
Key idea: the graph of h is the translation ![]() of the graph of
of the graph of ![]() (i.e., every point in the graph of
(i.e., every point in the graph of ![]() translates p units horizontally and q units vertically).
translates p units horizontally and q units vertically).
Finally, the respondent shows the purposefulness by emphasizing the key ideas and bringing mathematical closure to what students are doing:
Once students have graphed a few functions of the form![]() , I’d ask students to compare how constants p, q might be related to the constants b, c if
, I’d ask students to compare how constants p, q might be related to the constants b, c if ![]() is expanded to the form
is expanded to the form![]() . The purpose is to help students see that all quadratic functions of the form
. The purpose is to help students see that all quadratic functions of the form ![]() can be re-written as
can be re-written as![]() . And the key to accomplish this is via the so-called “completing the squares”.
. And the key to accomplish this is via the so-called “completing the squares”.
Different forms of quadratic function. Question 3.2 focuses on helping students understand how to rewrite the standard form into the vertex and root forms, both graphically and algebraically (i.e., completing the square)
As can be seen below, the respondent is purposeful about the key mathematical ideas that students need to understand:
The key mathematical ideas for this question are for students to understand that any quadratic function of the form ![]() can be re-written into: (1) the vertex form
can be re-written into: (1) the vertex form ![]() through the technique of completing the square; and (2) the root form
through the technique of completing the square; and (2) the root form ![]() if we know the root(s) of the quadratic function (and the roots are given by the quadratic formula, assuming discriminant b2 − 4ac ≥ 0).
if we know the root(s) of the quadratic function (and the roots are given by the quadratic formula, assuming discriminant b2 − 4ac ≥ 0).
In addition, the respondent demonstrates a deliberate effort at scaffolding ideas in a systematic and coherent way: showing the interconnectedness of ideas both geometrically and algebraically and scaffolding the reasoning from simple to complex and from specific to general. These features are well demonstrated in the following response:
So how would I go about accomplishing this teaching and learning goal?
(1) Standard form to vertex form:
I would graphically show the logic of completing the square and then algebraically manipulate the standard form to vertex form. In other words, I would start with the diagram approach first. Once students understand what “completing the square” looks like graphically, I’d go over how we to do the general case through algebraic manipulation.
Step 1: Graphically
Consider the expression ![]() where k, l are positive numbers. Then we can think of
where k, l are positive numbers. Then we can think of ![]() as
as![]() , which is equal to the area of the square with side length k, plus the areas of two rectangles each with side lengths k and
, which is equal to the area of the square with side length k, plus the areas of two rectangles each with side lengths k and![]() , as shown below.
, as shown below.
![]()
As the diagram shows, we could form a larger square with side length ![]() if we added in a square at the top right corner. What would be the area of such a square,
if we added in a square at the top right corner. What would be the area of such a square,![]() ?
?
![]()
Then the area of this larger square is![]() . Therefore, if we add
. Therefore, if we add ![]() to our original expression
to our original expression![]() , we “complete the square”. Symbolically:
, we “complete the square”. Symbolically:![]() .
.
Step 2: Algebraically
I would start with concrete cases of ![]() (e.g.,
(e.g.,![]() ) and ask students, what do we need to add to each of these expressions in order to be able to rewrite each one in the form
) and ask students, what do we need to add to each of these expressions in order to be able to rewrite each one in the form![]() ? Building upon the graphical approach in Step 1, students should see the following pattern:
? Building upon the graphical approach in Step 1, students should see the following pattern:![]() . I would summarize their work on the concrete cases with this general case, which can be transformed into:
. I would summarize their work on the concrete cases with this general case, which can be transformed into: ![]()
Then I would do concrete cases of ![]() (e.g.,
(e.g.,![]() ) and ask students, how can we rewrite each of the expressions in the form
) and ask students, how can we rewrite each of the expressions in the form![]() , plus some constant? Based on students work, I would summarize with the general case:
, plus some constant? Based on students work, I would summarize with the general case: ![]()
Finally, I would have concrete cases of ![]() (e.g.,
(e.g.,![]() ) and ask students, how can we rewrite the expressions so that each one has
) and ask students, how can we rewrite the expressions so that each one has ![]() in it?
in it?
Finally, the respondent is purposeful in terms of bringing a mathematical closure to what students are learning, namely, converting quadratic function from its standard form to vertex form:
Once they understand the concrete cases, I’d work with them through the general case in the function form:
![]()
I would ask students to determine what ?and ?? should be so that
![]()
Our conclusion would be ![]()
I would then ask students, where have we seen quadratic functions look like this? Hopefully they would recall
the form ![]() from work in question 1. Then, as a final exercise, I would have the students find the relationship between the constants, which would get the following:
from work in question 1. Then, as a final exercise, I would have the students find the relationship between the constants, which would get the following:![]() .
.
When helping students to understand how to convert quadratic function from standard form to root form, the respondent is explicit about using definition as a basis for logical reasoning:
Step 1: Definitions of “zero of a quadratic function” and “root of a quadratic equation”
We define ![]() to be a zero of a quadratic function
to be a zero of a quadratic function ![]() if
if![]() . We define
. We define ![]() to be a root of a quadratic equation
to be a root of a quadratic equation ![]() if
if ![]() is a solution to the equation
is a solution to the equation![]() . That means,
. That means,
a root of a quadratic equation ![]() is a zero of the quadratic function
is a zero of the quadratic function ![]() (and vice versa).
(and vice versa).
Using this definition, the respondent carefully scaffolds the ideas through a systematic and coherent progression by helping students understand: (1) the relationship between roots of a quadratic equation and x-intercepts of a quadratic function; (2) using this relationship to locate the x-intercepts of a quadratic function; and (3) transform the quadratic function from standard form to root form.
Why do we need different forms of quadratic functions? Questions 3.3 and 3.4 focus on different forms of quadratic functions. The primary purpose of these two scenario questions is to examine ways in which teachers help students to understand that each form of the quadratic function provides some information about the quadratic function and to see the connection between algebraic and geometric representations of quadratic function. An exemplary response again exhibits characteristics of coherence and purposefulness. For example, the following response shows a deliberate effort at showing the logical progression from using concrete examples to using general cases:
First, I’d ask students to graph a specific quadratic function, say![]() . I would expect them to do this by, first, rewriting the function into the form
. I would expect them to do this by, first, rewriting the function into the form ![]() as explained in question 2, and then, using
as explained in question 2, and then, using
the method outlined in question 1, they would translate the graph of ![]() to get the graph of
to get the graph of![]() . Then I’d ask them to work in groups or pairs to figure out the following:
. Then I’d ask them to work in groups or pairs to figure out the following:
1. At what value (s) of x does the graph intersect the x-axis? What does it mean when the graph of the function intersects the x-axis?
2. Where is the line of symmetry? Draw it.
At what value of x does the function achieve its maximum or minimum value? How do you know? When does a quadratic function have a maximum value? When does it have a minimum value?
Not only that, the respondent connects mathematical ideas students are learning now with what they were doing previously:
The first set of questions relates back to question 2, (2). There we showed how to find the roots of the quadratic equation algebraically (and by connecting Step 2 of (1) and Step 3 of (2) we can get the quadratic formula, which is a quick and mechanical way to get the roots directly from the quadratic function in standard form, assuming the discriminant is greater than or equal to zero). We can also find the roots of the quadratic equation (which are the x-intercepts or zeros of the quadratic function) by using the graph: we see that the graph of
![]() intersects the x-axis k units above the vertex
intersects the x-axis k units above the vertex![]() . Because the graph of
. Because the graph of ![]() is congruent to the graph of f (as discussed in question 1), we can find the x-intercepts by finding the x-values when
is congruent to the graph of f (as discussed in question 1), we can find the x-intercepts by finding the x-values when![]() . The result is
. The result is![]() , which means the x-intercepts of f are
, which means the x-intercepts of f are ![]() from the axis of symmetry
from the axis of symmetry ![]() (see graph below).
(see graph below).
![]()
In addition to helping students connect mathematical ideas learned previously, the respondent also is deliberate at helping students to connect the algebraic and geometric representations:
By looking at the graph, students should also notice that the vertex is the point at which the function achieves
its maximum (when the constant a < 0) or minimum value (when the constant a > 0). The vertex is ![]() because, if a > 0 then
because, if a > 0 then ![]() and thus
and thus ![]() so f achieves its minimum when
so f achieves its minimum when![]() , i.e., x = h. The argument is similar when a < 0.
, i.e., x = h. The argument is similar when a < 0.
Finally, the respondent is purposeful at emphasizing key mathematical ideas in order to bring a mathematical closure to the concepts that students are learning:
At the conclusion of the exercise, I would ask, so what is the value of writing the quadratic function in the
form![]() ? I would expect students to say: it tells us the vertex, the axis of symmetry, and how to translate the graph of
? I would expect students to say: it tells us the vertex, the axis of symmetry, and how to translate the graph of ![]() to the graph of f. I would then ask, so what is the value of the root form
to the graph of f. I would then ask, so what is the value of the root form
(which they learned to derive in Question 2)? I would expect students to say: it tells us the roots of the quadratic equation, which are the x-intercepts, as well as the zeros, of the quadratic function.
In this way, students can see that the vertex form and root form provide them with all there is to know about the graph of a quadratic function. However, it’s the standard form that immediately tells us the quadratic function is a member of the broader family of polynomial functions. Therefore, each form tells us something about the function but not everything (the vertex form doesn’t immediately give us the roots, the root form doesn’t immediately give us the vertex, the standard form doesn’t tell us much about how the graph looks).
To summarize, the cases we show exemplify precision, coherence, and purposefulness, key attributes of a deep content understanding for teaching K-12 students. Throughout, these responses demonstrate a consistent effort at emphasizing key mathematical ideas, the logical progression of mathematical concepts, and the connectedness among different concepts, procedures, and ideas. In addition, responses show careful attention to scaffolding ideas to students in a systematic and coherent way: from simple to complex, from specific examples to general cases.