A Multinomial Theorem for Hermite Polynomials and Financial Applications ()
1. Introduction
Hermite polynomials are widely used in finance, for various purposes including option pricing and risk man- agement. Madan and Milne [1] have built a framework applying functional analysis results to the particular case of Hermite polynomials and inferred pricing formulas for general payoffs expressed as linear combinations of Hermite polynomials. They applied their framework to the simple case of calls to determine the implicit basis prices in the market data and imply an empirical futures price law. More recently, a series of papers have de- veloped closed-form series expansions for various models: Tanaka, Yamada and Watanabe [2] developed ap- proximations of the prices of some interest derivatives; Schloegl [3] adapted this type of expansions to multi- period models. On the other hand, Buet-Golfouse and Owen [4] , Voropaev [5] , and Owen et al. [6] applied the Mehler formula and multivariate Hermite expansions to the allocation of risk measures in a portfolio of financial instruments.
The aim of this paper is to derive a theoretical framework that underlies many usages of Hermite polynomials in finance. In particular, the first main result of this paper is to have established a link between the probability distribution of the underlying factor and the empirical prices of Hermite functions. The second main result is a multinomial expansion theorem for Hermite polynomials (and its extensions). Both provide a solid foundation to derive the no-arbitrage price of a contingent claim stemming from a linear combination of factors.
The article is organised as follows: in the first section we state some basic facts about univariate and multi- variate Hermite polynomials; the second section is devoted to the justification of expansions on the basis of Hermite functions and demonstrates the link between implicit prices of Hermite polynomials and the probability distribution of the underyling assets under the forward probability measure; the third section states and proves a multinomial theorem for Hermite polynomials with extensions and examples provided in the fourth and fifth sections; the sixth and final sections are dedicated to the application of the multinomial theorem for Hermite polynomials to pricing under no-arbitrage. Finally, empirical applications of the described methodology can be found in [4] and [6] .
2. A Few Facts about Hermite Polynomials
Our objective is not to give a full account of the literature on Hermite polynomials but simply to recall some definitions and properties (see Abramovitz and Stegun [7] for more information). Let  be the standard normal density and
be the standard normal density and 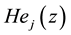 be the
be the  Hermite polynomial satisfying
Hermite polynomial satisfying 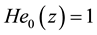 and for any
and for any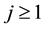 ,
,
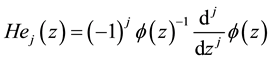 . An alternative definition is via the exponential generating function
. An alternative definition is via the exponential generating function
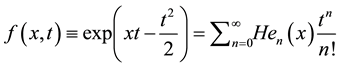 .
.
The two most important properties are the recurrence relationship and the orthogonality property. The re- currence relationship states that ,
, :
:
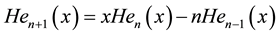 (1)
(1)
and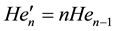 , whilst the orthogonality property states that for all
, whilst the orthogonality property states that for all 
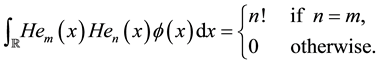 (2)
(2)
Explicit and inverse explicit expressions are available for Hermite polynomials: for all 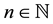 and
and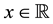 , the following identities hold:
, the following identities hold:
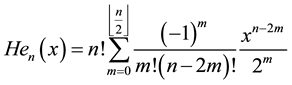
![]() (3)
(3)
N-multivariate Hermite polynomials are usually defined as the product of N univariate Hermite polynomials. Let us first clarify some notations used in the rest of the paper:![]() ,
, ![]() are vectors respectively in
are vectors respectively in ![]() and
and![]() ,
, ![]() is the Euclidian scalar product in
is the Euclidian scalar product in![]() , while
, while ![]() refers to the generalised factorial, i.e.
refers to the generalised factorial, i.e.![]() , so that
, so that ![]() for any
for any![]() , and
, and ![]() is the order of n.
is the order of n.
![]() is defined as
is defined as
![]() (4)
(4)
The orthogonality property can readily be adapted to the multivariate case component by component:
![]() (5)
(5)
Let us now consider the Hilbert space ![]() of functions that are square integrable with respect to the measure P defined by the density
of functions that are square integrable with respect to the measure P defined by the density
![]() (6)
(6)
An orthonormal basis ![]() for H is given by the polynomial functions (also sometimes called “Hermite
for H is given by the polynomial functions (also sometimes called “Hermite
functions”)![]() :
: ![]()
Using standard arguments in functional analysis, an arbitrary claim ![]() in H may be expressed in the basis
in H may be expressed in the basis ![]() as
as
![]() (7)
(7)
where the coefficients ![]() are obtained by the Hilbertian inner product
are obtained by the Hilbertian inner product
![]() (8)
(8)
To summarise, we have built an orthonormal basis in which to decompose functions that are square-integrable against the standard N-dimensional Gaussian distribution
![]() (9)
(9)
but have actually made no assumption on the distribution of the vector of factors![]() . Indeed, this is the subject tackled by the following section.
. Indeed, this is the subject tackled by the following section.
3. Implied Prices and Probability Distributions
In this section, we demonstrate the link between two notions that are used separately in the literature: the implicit prices of Hermite polynomials (as in Madan and Milne (1994), where the payoff is expanded in Hermite polynomials) and the risk-neutral distribution of the vector of factors ![]() (see Yamada and Watanabe [2] and Schloegl [3] where it is the factors’ density that is expanded in Hermite polynomials and not the payoff as such).
(see Yamada and Watanabe [2] and Schloegl [3] where it is the factors’ density that is expanded in Hermite polynomials and not the payoff as such).
We consider a financial market on a period ![]() with
with![]() :
: ![]() where
where ![]() is the uni- verse,
is the uni- verse, ![]() the chosen
the chosen ![]() -algebra (assumed here to be the Borelian tribe) and
-algebra (assumed here to be the Borelian tribe) and ![]() the market’s probability mea- sure (a priori, it is not necessarily a risk neutral measure, as we can choose it to be the physical measure). We denote by
the market’s probability mea- sure (a priori, it is not necessarily a risk neutral measure, as we can choose it to be the physical measure). We denote by ![]() the risk-free rate and
the risk-free rate and ![]() the related zero-coupon with time horizon T. Note that we consider this simple framework to lay out the assumptions and theorems, but it could be adapted to a multi- period setting. In the definition below, we summarise the key aspects of a complete market (see Portait and Poncet [8] ).
the related zero-coupon with time horizon T. Note that we consider this simple framework to lay out the assumptions and theorems, but it could be adapted to a multi- period setting. In the definition below, we summarise the key aspects of a complete market (see Portait and Poncet [8] ).
Proposition 1. A self-financing strategy is admissible if its terminal value is a random variable whose second moment is well-defined (i.e., it is square-integrable), a contingent claim is attainable if there exists a self- financing strategy whose terminal value is equal to the contingent claim almost surely (in particular, it has to be square integrable), and the market is complete if all contingent claims are attainable. A system of prices V is an application from the set of contingent claims to ![]() and it is said to be viable if it is compatible with the no- arbitrage condition: in particular, it is a linear form.
and it is said to be viable if it is compatible with the no- arbitrage condition: in particular, it is a linear form.
From now on, we assume the market to be complete and to satisfy the no arbitrage condition and consider ![]() to be the risk-neutral measure (and to be absolutely continuous with respect to the Lebesgue measure).
to be the risk-neutral measure (and to be absolutely continuous with respect to the Lebesgue measure).
If![]() , then it is attainable and has a unique price
, then it is attainable and has a unique price ![]() (V is also unique) and further assum-
(V is also unique) and further assum-
ing that![]() , it can be expanded in the basis of Hermite polynomials. This results in the possibility
, it can be expanded in the basis of Hermite polynomials. This results in the possibility
to express the contingent claim ![]() as a linear combination of the basis elements, namely the Hermite functions
as a linear combination of the basis elements, namely the Hermite functions![]() , which can be seen as simpler contingent claims. Using the linearity of the price functional V and Cauchy-Schwarz inequality (see Theorem 2.2 in Madan and Milne [1] ), this finally yields the market value of
, which can be seen as simpler contingent claims. Using the linearity of the price functional V and Cauchy-Schwarz inequality (see Theorem 2.2 in Madan and Milne [1] ), this finally yields the market value of ![]() as
as
![]() (10)
(10)
with ![]() the (implicit) market price of
the (implicit) market price of![]() .
.
Theorem 1. Under the assumption that V is continuous there exists a unique ![]() such that for all
such that for all![]() ,
,
![]() (11)
(11)
Proof. We already know that V is a linear form on ![]() (which is a Hilbert space) and under the theorem’s assumption, it is also continuous. Hence, using the Riesz representation theorem (see Brezis [9] ), we
(which is a Hilbert space) and under the theorem’s assumption, it is also continuous. Hence, using the Riesz representation theorem (see Brezis [9] ), we
can infer the existence of a unique ![]() such that
such that![]() . □
. □
We now turn to the probability density function ![]() and its (unique) Radon-Nikodym derivative
and its (unique) Radon-Nikodym derivative ![]() with respect to the reference measure P defined as the N-variate standard Gaussian distribution in the previous section, that is:
with respect to the reference measure P defined as the N-variate standard Gaussian distribution in the previous section, that is:
![]() (12)
(12)
so that, finally, we have
![]() (13)
(13)
Definition 1. Under the same assumptions, ![]() is called the futures price law of
is called the futures price law of ![]() with respect to the probability measure P.
with respect to the probability measure P.
The meaning of the futures price law can be derived as follows: rewriting ![]() as
as
![]() (14)
(14)
it becomes clear that ![]() is the inner product in
is the inner product in ![]() of the payoff and the empirical prices law (which makes sense if the latter is square integrable). We now give a theorem linking the futures price law, prices of the basis elements and Hermite expansions to translate this observation in rigorous terms.
of the payoff and the empirical prices law (which makes sense if the latter is square integrable). We now give a theorem linking the futures price law, prices of the basis elements and Hermite expansions to translate this observation in rigorous terms.
Theorem 2. The following statements are equivalent:
i) There exists a sequence![]() , such that
, such that ![]() and
and ![]() for any
for any ![]() such that
such that![]() ;
;
ii)![]() ;
;
iii) There exists a sequence![]() , such that
, such that ![]() and
and![]() .
.
Remark 1. This result is a slightly different view of Madan and Milne’s Theorem 4.1 [1] because our set of assumptions is minimal and it was derived following the path of the Riesz representation formula. In particular Madan and Milne’s assumption that ![]() is uniformly bounded above and below implies that
is uniformly bounded above and below implies that ![]() .
.
Proof. Clearly, ii) implies iii). To prove that iii) implies ii), we apply Lemma 5.1. in Ch. 5 of Brezis [9] : the
sequence ![]() is in
is in![]() , its components are orthogonal to each other and
, its components are orthogonal to each other and
![]() (15)
(15)
so that
![]() (16)
(16)
Then, noting![]() , it comes that
, it comes that ![]() exists and
exists and
![]() .
.
It now remains to prove that i) is equivalent to iii). iii) implies i) is a simple consequence of the inner product in a Hilbert space:
![]() (17)
(17)
Starting from i), we have that ![]() so that we can build
so that we can build ![]() which verifies
which verifies
![]()
for any contingent claim ![]() that is also in
that is also in![]() . Hence,
. Hence, ![]() must equal
must equal![]() . □
. □
This theorem thus shows that under mild conditions (i.e. that the probability ![]() is not too “different” from P) the futures price law can be expanded in the basis of Hermite functions and is such that its coefficients are the prices of the Hermite functions under the risk neutral measure. But so far, we have simply considered V from a theoretical perspective and since we want to prove the link between our results and Yamada and Watanabe’s expansions in terms of the density of the factors
is not too “different” from P) the futures price law can be expanded in the basis of Hermite functions and is such that its coefficients are the prices of the Hermite functions under the risk neutral measure. But so far, we have simply considered V from a theoretical perspective and since we want to prove the link between our results and Yamada and Watanabe’s expansions in terms of the density of the factors![]() , we can express it directly as
, we can express it directly as
![]() (18)
(18)
where r is the risk-free rate.
Introducing the risk-neutral T-forward measure![]() , the following holds:
, the following holds:
![]() (19)
(19)
where ![]() is the price of the zero-coupon of horizon T (see [8] for details). A first but important remark is
is the price of the zero-coupon of horizon T (see [8] for details). A first but important remark is
that if r is assumed to be bounded, then ![]() so that we can consider contingent claims
so that we can consider contingent claims
under either probability measure. As in Tanaka et al. [2] , the assumption is made that the probability distribution g of ![]() under the T-forward measure can be expressed as
under the T-forward measure can be expressed as
![]() (20)
(20)
A sufficient and necessary condition for g to be a valid density function is to have
・ ![]() .
.
・ and ![]() for all
for all![]() .
.
Schloegl [3] discusses ways to ensure that the second condition is met in practice when the summation is taken over a finite number of Hermite functions. Now, using the pricing formula under the T-forward measure ![]() leads to:
leads to:
![]() (21)
(21)
When the various assumptions of the theorems above are verified, it comes
![]() (22)
(22)
whence the following theorem linking the futures price law and the T-forward probability density function of the factors holds.
Theorem 3. The implied prices ![]() of Hermite functions and the coefficients
of Hermite functions and the coefficients ![]() of the the T-forward probability density function satisfy the fundamental equality
of the the T-forward probability density function satisfy the fundamental equality
![]() (23)
(23)
for all![]() .
.
A direct application of this theorem is the determination of price elements ![]() from the moments of the distribution g and vice-versa. For the sake of clarity we consider the case
from the moments of the distribution g and vice-versa. For the sake of clarity we consider the case ![]()
![]() in the rest of the section, but the results can easily be extended to the multivariate case.
in the rest of the section, but the results can easily be extended to the multivariate case.
Lemma 1. Let ![]() denote the
denote the ![]() moment of the distribution g:
moment of the distribution g:![]() . Then
. Then
![]() (24)
(24)
![]() (25)
(25)
Proof. It suffices to use the explicit and inverse explicit formulas and perform some simple algebra to obtain both results. □
Since in the financial framework considered so far![]() , all moments of the distribution g can be
, all moments of the distribution g can be
implied from the prices of the orthonormal basis![]() . Now that the foundations of the framework have been laid, we can move to another result, namely the Hermite multinomial theorem.
. Now that the foundations of the framework have been laid, we can move to another result, namely the Hermite multinomial theorem.
4. Factor Models and the Hermite Multinomial Theorem
Considering several factors at the same time and linear combinations of those is at the core of many financial models: Fama and French’s three-factor model for asset returns, Brennan and Schwarz’ two-factor model, Lang- estieg’s multi-factor model for interest rates or the multi-factor Merton-Vasicek model for example. Supposing that we have a financial instrument depending on a linear combination ![]() of the original factors, we would like to expand this instrument in the basis of Hermite functions
of the original factors, we would like to expand this instrument in the basis of Hermite functions![]() : this has implications in terms of pricing and risk management as the factors can represent some macroeconomic variables that one might wish to stress. This section therefore states and proves a multinomial theorem for Hermite polynomials and corrects a previous expansion given by Voropaev in [5] .
: this has implications in terms of pricing and risk management as the factors can represent some macroeconomic variables that one might wish to stress. This section therefore states and proves a multinomial theorem for Hermite polynomials and corrects a previous expansion given by Voropaev in [5] .
Let us start by considering the example of a two-factor model, i.e.![]() . Noting that
. Noting that ![]() and
and ![]() for any
for any ![]() and
and![]() , it simply comes
, it simply comes
![]() . (26)
. (26)
Let us now compute separately:
![]() (27)
(27)
Hence, in the case where![]() , the following identity holds:
, the following identity holds:
![]() . (28)
. (28)
The condition ![]() is absolutely key in the equality and is called the “factor loading condition” in credit risk modelling. It can actually be seen as a normalisation constraint: if
is absolutely key in the equality and is called the “factor loading condition” in credit risk modelling. It can actually be seen as a normalisation constraint: if ![]() and
and ![]() are independent and normalised (i.e. have mean 0 and variance 1), then
are independent and normalised (i.e. have mean 0 and variance 1), then ![]() will have mean 0 and variance 1 if and only if
will have mean 0 and variance 1 if and only if![]() . We can now proceed to a general version of the theorem. This result did not have a general statement and proof widely available, but given its simplicity, it might have been derived in a different context.
. We can now proceed to a general version of the theorem. This result did not have a general statement and proof widely available, but given its simplicity, it might have been derived in a different context.
Theorem 4. Let ![]() and
and![]() . Then for all
. Then for all ![]() s with
s with ![]() such that
such that![]() ,
,
![]() . (29)
. (29)
Remark 2. The theorem can be restated in a more condensed form and in terms of Hermite functions as
![]() . (30)
. (30)
We offer two proofs of the result, one based on the repeated application of the recursion property (see the Appendix) and the other on the generating function of Hermite polynomials to show how powerful and different these two tools are for analysing relationships involving Hermite polynomials. They offer different insights in the manipulation of Hermite polynomials and are a good exercise for the reader.
Let us now move to a demonstration based on the exponential generating function.
Proof. We have that
![]() (31)
(31)
Hence, comparing the first and the last lines of this equation we must have
![]() (32)
(32)
which yields the result. □
To show how powerful this simple tool is, we provide some direct extensions and examples in the next two sections.
5. Two Extensions of the Multinomial Theorem
It is possible to easily extend this result to multivariate Hermite polynomials and to weights which do not re- spect the factor loading condition.
Looking first at the case of multivariate Hermite polynomials, the idea is to consider a linear combination of
multivariate factors ![]() so that
so that ![]() is yet another vector.
is yet another vector.
Theorem 5. Let![]() ,
, ![]() ,
, ![]() such that
such that ![]() and
and![]() . Then the following equality holds:
. Then the following equality holds:
![]()
with ![]() the vector of the
the vector of the ![]() coordinates of the factors.
coordinates of the factors.
Proof. It suffices to apply the multinomial theorem for Hermite polynomials to each of the univariate Hermite
polynomials![]() . □
. □
Another extension, perhaps more important for practitioners, is to consider the case where the factor loading condition is not verified. For the sake of simplicity, let us go back to the univariate case and suppose that ![]() (but still
(but still![]() ). We can state the general multinomial theorem for Hermite polynomials as follows:
). We can state the general multinomial theorem for Hermite polynomials as follows:
Theorem 6. Under the assumption that ![]() (i.e.
(i.e.![]() ), the following identity is checked:
), the following identity is checked:
![]() . (33)
. (33)
In the proof, we make use of the following lemma from Schloegl (2013) [3] :
Lemma 2. Let![]() . Then
. Then
![]() . (34)
. (34)
Proof. (Of the theorem) We can rewrite ![]() as
as
![]() . (35)
. (35)
We derive the following equality from the intermediary lemma:
![]() (36)
(36)
□
Remark 3. In the same vein, it is also possible to infer a similar but even more general result for
![]() (37)
(37)
where ![]() and
and ![]() and even extend it to the multivariate case; we leave the computational details to the interested reader.
and even extend it to the multivariate case; we leave the computational details to the interested reader.
6. Revisiting the Orthogonality Property and the Mehler Formula
Let us revisit the orthogonality property, but this time in presence of correlation. Our aim is to compute![]() , where X and Y are two standard Gaussian random variables with correlation coefficient
, where X and Y are two standard Gaussian random variables with correlation coefficient![]() . To do so we prove the following theorem.
. To do so we prove the following theorem.
Theorem 7. For any![]() , the following identity is true:
, the following identity is true:
![]() (38)
(38)
with ![]() the Kronecker symbol and
the Kronecker symbol and ![]() the bivariate Gaussian probability distribution function.
the bivariate Gaussian probability distribution function.
Proof. Another way of expressing this double integral is to write it as
![]() . (39)
. (39)
Using the binomial formula, which is a particular case of the multinomial formula that we have proved, we have
![]() . (40)
. (40)
Thus,
![]() (41)
(41)
The “correlated orthogonality” property has been proved. □
Based on this simple observation, a simple and elegant proof of the Mehler formula can be given:
Corollary 1. (Mehler formula) The bivariate normal probability density function ![]() satisfies the following equality (for
satisfies the following equality (for ![]() and
and![]() ):
):
![]() . (42)
. (42)
Proof. It suffices to expand ![]() in the Hermite polynomial basis:
in the Hermite polynomial basis:
![]() (43)
(43)
and use the correlated orthogonality property. □
The Mehler formula is of special importance since it can be used as a foundation in credit-risk modelling, as in Voropaev [5] , to compute the expected value of a portfolio V of K financial instruments![]() ,
, ![]() , conditional on the value of a factor, say Y. Suppose that each
, conditional on the value of a factor, say Y. Suppose that each ![]() is a function (verifying all necessary inte- grability conditions) of a random variable
is a function (verifying all necessary inte- grability conditions) of a random variable ![]() which depends linearly on a systemic factor Y and an idio- syncratic (i.e. instrument-specific) factor
which depends linearly on a systemic factor Y and an idio- syncratic (i.e. instrument-specific) factor ![]() (
(![]() ’s are assumed to be mutually independent and to follow standard Gaussian distributions):
’s are assumed to be mutually independent and to follow standard Gaussian distributions):
![]() . (44)
. (44)
Thus,![]() . Focusing on
. Focusing on![]() , we can write the following equations:
, we can write the following equations:
![]() (45)
(45)
where we have defined![]() , which does not depend on the decomposition in
, which does not depend on the decomposition in
terms of Y and![]() . This is extremely useful as it can be used for assessing the impact of Y on the whole port- folio (for instance by computing the value-at-risk of the conditional expected loss, and so on).
. This is extremely useful as it can be used for assessing the impact of Y on the whole port- folio (for instance by computing the value-at-risk of the conditional expected loss, and so on).
7. The Multinomial Factorisation Theorem and Arbitrage
Going back to our framework where the market has no arbitrage and is complete, we wish to determine the relationship between the implied prices of the basis and those of a linear combination of the underlying factors. To make things clearer suppose that we are looking at a payoff ![]() whose underlying factor
whose underlying factor ![]() is a linear combination of N factors (as previously, we note
is a linear combination of N factors (as previously, we note![]() ) with a vector
) with a vector ![]() of factor loadings whose norm is 1:
of factor loadings whose norm is 1: ![]() with
with![]() . Then:
. Then:
![]() (46)
(46)
which can be restated in terms of Hermite functions as ![]() where
where![]() .
.
On the one hand, we have the basis of Hermite functions to expand the payoff ![]() as a function of
as a function of![]() :
:
![]() (47)
(47)
where![]() .
.
On the other hand, we can express the payoff ![]() of
of ![]() as a multivariate function
as a multivariate function ![]() of
of ![]() by writing that
by writing that![]() . Applying a multivariate expansion this time, we obtain that
. Applying a multivariate expansion this time, we obtain that
![]() (48)
(48)
where
![]() (49)
(49)
Since![]() , using the valuation formula, by no arbitrage, we would necessarily have
, using the valuation formula, by no arbitrage, we would necessarily have
![]() so that
so that
![]() (50)
(50)
where ![]() is the potential implied price of
is the potential implied price of ![]() for all k and
for all k and ![]() is the known implied price of
is the known implied price of
![]() .
.
Thanks to the multinomial factorisation, we have that
![]() . (51)
. (51)
By identifying terms in this multivariate polynomial function, we obtain
![]() . (52)
. (52)
Turning to the prices, we see that
![]() (53)
(53)
On the other hand, we have that![]() . Bringing both equations together, we can write the following equality:
. Bringing both equations together, we can write the following equality:
![]() (54)
(54)
and infer the theorem:
Theorem 8. Since the function ![]() is a generic payoff, by analysing the series coefficient by coefficient, we finally obtain that
is a generic payoff, by analysing the series coefficient by coefficient, we finally obtain that
![]() (55)
(55)
Proof. We have shown that ![]() was a valid choice for
was a valid choice for![]() . Let us show that it is the only one by applying no-arbitrage pricing arguments.
. Let us show that it is the only one by applying no-arbitrage pricing arguments.
Indeed, suppose that there exists ![]() such that
such that ![]() (for clarity’s sake,
(for clarity’s sake,![]() ). Let us then choose
). Let us then choose![]() , which is a valid payoff, so that we have
, which is a valid payoff, so that we have![]() . A portfolio can then be built by buying the
. A portfolio can then be built by buying the
duplicated payoff at price![]() , i.e.
, i.e.![]() , and shorting it at price
, and shorting it at price![]() .
.
Since the payoffs ![]() and
and ![]() are equal, we have built a portfolio that displays an arbitrage. □
are equal, we have built a portfolio that displays an arbitrage. □
To summarise, we have shown that it was possible to express explicitly the coefficients ![]() and the prices
and the prices ![]() as functions of the coefficients
as functions of the coefficients ![]() and the prices
and the prices![]() . The strength of this theorem is to make explicit the no arbitrage relationship between the empirical prices of the Hermite polynomials and the empirical price of a linear combination of the factors, which leads to the formulation of the following result:
. The strength of this theorem is to make explicit the no arbitrage relationship between the empirical prices of the Hermite polynomials and the empirical price of a linear combination of the factors, which leads to the formulation of the following result:
Theorem 9. We have determined the futures price law density of ![]() denoted by
denoted by ![]() as
as
![]() . (56)
. (56)
8. Concluding Remarks
This paper proposes a simple way of expanding the Hermite polynomial of a linear combination of factors into simpler elements. This method allows us to prove the celebrated Mehler formula in a very simple way, but also enables us to derive the empirical prices of functions of linear combination of factors in a market with no arbi- trage and facilitates credit risk modelling. Practical illustrations of the theoretical framework developed in this paper can be found in [2] - [6] . We have built on the theory developed by Madan and Milne and highlighted the relationship that existed between their results and other recent results obtained in the field of pricing. Using a multinomial theorem for Hermite polynomials, we have shown how to tackle expressions including more than one factor.
The main assumption made throughout the paper is the existence of a payoff’s or probability density func- tion’s expansion in the basis of Hermite polynomials. Although this is quite restrictive (it implies the existence of all moments in the latter case for instance), it does allow for significant deviations from the benchmark case of standard Gaussian distributions. The computational approach at hand indeed permits to only consider a series of simple computations rather than a difficult and time consuming one. It offers a practical analytical alternative to full-fledged Monte Carlo simulations.
Acknowledgements
The author would like to thank Anthony Owen and James Bryers for initiating this work on the use of Hermite polynomials in finance and their insightful remarks. Thanks also go to Li Shanqiu and to two anonymous referees for their helpful comments.
Appendix
In this appendix we give an alternative proof of the multivariate theorem for Hermite polynomials
Proof. The cases ![]() and
and![]() , for all N, are obvious since
, for all N, are obvious since ![]() and
and![]() . Let us now suppose that the property holds for all k such that
. Let us now suppose that the property holds for all k such that![]() .
.
Using the recurrence formula
![]() (57)
(57)
we can write that
![]() (58)
(58)
We can split the above expressions into the three pieces:
![]() (59)
(59)
![]() (60)
(60)
![]() (61)
(61)
Our aim is to demonstrate ![]() where
where
![]() (62)
(62)
We start by proving ![]() and then move on to showing that
and then move on to showing that![]() .
.
![]() (63)
(63)
Turning to![]() , it now boils down to making the change of variables
, it now boils down to making the change of variables ![]() to obtain the equality
to obtain the equality
![]() .
.
Similarly, in![]() , using the change of variables
, using the change of variables![]() , we obtain
, we obtain
![]() (64)
(64)
Finally, the result has been proved. □