Presence of Heat on an Infinite Plate with a Curvilinear Hole Having Two Poles ()
1. Introduction
The boundary value problems for isotropic performed plates have been discussed by several authors. Some authors used Laurant’s theorem [1] -[8] to express each complex potential as a power series, and others [9] -[16] used complex variable method of Cauchy integral. The extensive literature on the isotropic is now available and we can only mention a few recent interesting investigations in refs [17] -[26] .
In thermoelastic problems for elastic media, the first and second boundary value problems are equivalent to two finite analytic functions 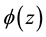 and
and 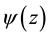 of one complex argument
of one complex argument . These functions must satisfy the boundary condition,
. These functions must satisfy the boundary condition,
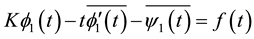 (1)
(1)
where t denotes the affix of a point on the boundary. In terms of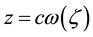 ,
,  ,
, 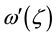 does not vanish or become infinite for
does not vanish or become infinite for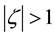 , where the infinite region is outside a unit circle
, where the infinite region is outside a unit circle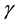 . For the first fundamental boundary value problems or the called stress boundary value problems,
. For the first fundamental boundary value problems or the called stress boundary value problems,  ,
,  is a given function of stress. While for
is a given function of stress. While for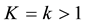 ,
,  is a given function of displacement called the thermal conductivity; we have the second fundamental boundary value problems called the displacement boundary value problems.
is a given function of displacement called the thermal conductivity; we have the second fundamental boundary value problems called the displacement boundary value problems.
The complex potential functions ![]() and
and ![]() take the following forms, see [23]
take the following forms, see [23]
![]() (2)
(2)
and,
![]() (3)
(3)
where, ![]() are the components of the resultant vector of all external forces acting on the boundary and
are the components of the resultant vector of all external forces acting on the boundary and ![]() are complex constants. Generally the two complex functions
are complex constants. Generally the two complex functions ![]() and
and ![]() are single value analytic functions within the region outside the unit circle
are single value analytic functions within the region outside the unit circle ![]() and
and![]() . In [27] , Muskhelishvili used the rational mapping,
. In [27] , Muskhelishvili used the rational mapping,
![]() (4)
(4)
for solving the problem of stretching of an infinite plate weakened by an elliptic hole. Sokolonikoff [3] used the same rational mapping of Equation (4) to solve the problem of elliptical ring, where the Laurant’s theorem is used. This transformation of Equation (4) conformally maps the infinite domain bounded internally by an ellipse onto the domain outside the unit circle ![]() in the
in the ![]() -plane. The application of the Hilbert problem is used by Muskhelishvili [27] to discuss the case of a stretched infinite plate weakened by a circular cut. England [1] considered an infinite plate which is weakened by a hypotrochoid hole, conformally mapped onto a unit circle
-plane. The application of the Hilbert problem is used by Muskhelishvili [27] to discuss the case of a stretched infinite plate weakened by a circular cut. England [1] considered an infinite plate which is weakened by a hypotrochoid hole, conformally mapped onto a unit circle ![]() by the transformation mapping
by the transformation mapping
![]() (5)
(5)
where ![]() does not vanish or become infinite outside the unit circle
does not vanish or become infinite outside the unit circle![]() , and solve the boundary value problems.
, and solve the boundary value problems.
The main reason for interest in this mapping is that the general shape of the hypotrochoids is curvilinear polygons, for n = 1 ellipse, for n = 2 a curvilinear triangle, for n = 3 a curvilinear square… etc. In previous papers (Abdou et al. [9] -[15] [28] [29] ), the complex variable method has been applied to solve the first and second fundamental problems for the same domain of the infinite plate with general curvilinear hole c conformally mapped on the domain outside a unit circle by using respectively, the rational mapping functions
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
and
![]() (9)
(9)
In this paper, the complex variable method has been applied to solve the first and second fundamental problems for the same previous domain of the infinite plate with a general curvilinear hole C, with three poles and presence of heat, conformally mapped on the domain outside a unit circle ![]() by the rational mapping functions
by the rational mapping functions
![]() (10)
(10)
where![]() ,
, ![]() ,
, ![]() and
and ![]() are real parameters restricted such that
are real parameters restricted such that ![]() does not vanish or become infinite outside the unit circle
does not vanish or become infinite outside the unit circle![]() . Consider a heat
. Consider a heat ![]() flowing uniformly in the direction of the negative y-axis, where the increasing temperature
flowing uniformly in the direction of the negative y-axis, where the increasing temperature ![]() is assumed to be constant across the thickness of the layer, i.e.
is assumed to be constant across the thickness of the layer, i.e.![]() , and q is the constant temperature gradient. The uniform flow of heat is distributed by the presence of an insulated curvilinear hole C. The heat equation satisfies the relations,
, and q is the constant temperature gradient. The uniform flow of heat is distributed by the presence of an insulated curvilinear hole C. The heat equation satisfies the relations,
![]() (11)
(11)
![]() (12)
(12)
where n is the unit vector perpendicular to the surface.
Neglecting the variation of the strain and the stress with respect to the thickness of the layer, the thermoelastic potential function ![]() satisfies the formula (see [14] ),
satisfies the formula (see [14] ),
![]() (13)
(13)
where ![]() is a scalar which presents the coefficient of the thermal expansion and
is a scalar which presents the coefficient of the thermal expansion and ![]() is Poisson’s ratio. Assume that the force of the layer is free of applied loads.
is Poisson’s ratio. Assume that the force of the layer is free of applied loads.
In this case, formula (1) for the first and second boundary value problems respectively takes the following forms,
![]() (14)
(14)
![]() (15)
(15)
where the applied stresses ![]() and
and ![]() are prescribed on the boundary of the plane; s is the length measured from an arbitrary point; u and v are the displacement components; G is the shear modulus and
are prescribed on the boundary of the plane; s is the length measured from an arbitrary point; u and v are the displacement components; G is the shear modulus and ![]() represents the thermoelastic potential function. Also, here the applied stresses
represents the thermoelastic potential function. Also, here the applied stresses ![]() and
and ![]() must satisfy the following (see [14] ),
must satisfy the following (see [14] ),
![]() (16)
(16)
![]() (17)
(17)
where ![]() and
and ![]() are the components of stresses which are given by the following relations,
are the components of stresses which are given by the following relations,
![]() (18)
(18)
![]() (19)
(19)
where ![]() is the coefficient of heat transfer.
is the coefficient of heat transfer.
The rational mapping ![]() maps the boundary C of the given region occupied by the middle plane of the layer in the z-plane onto the unit circle
maps the boundary C of the given region occupied by the middle plane of the layer in the z-plane onto the unit circle ![]() in the
in the ![]() -plane. Curvilinear coordinates
-plane. Curvilinear coordinates ![]() are thus introduced into the z-plane, which are the maps of the polar conditions in the
are thus introduced into the z-plane, which are the maps of the polar conditions in the ![]() -plane as given by
-plane as given by![]() ,
,![]() . By using the transformation
. By using the transformation![]() , Equation (1) reduces to,
, Equation (1) reduces to,
![]() (20)
(20)
the last formula represents the first and second boundary value problems in the ![]() -plane.
-plane.
In this study, we use the rational mapping (10) to map the curvilinear hole C of the infinite viscoelastic fluid layer outside a unit circle![]() . Then, we use the properties of Cauchy integral to obtain the two complex potential functions (Goursat functions). After that, we determine the components of stresses. We establish many applications and special cases from this work.
. Then, we use the properties of Cauchy integral to obtain the two complex potential functions (Goursat functions). After that, we determine the components of stresses. We establish many applications and special cases from this work.
2. The Rational Mapping
The mapping function (10) maps the curvilinear hole C in z-plane onto the domain of the outside unit circle in ![]() -plane under the conditions that
-plane under the conditions that ![]() does not vanish or become infinite outside the unit circle
does not vanish or become infinite outside the unit circle![]() . The following graphs give the different shapes of the rational mapping (10), see Figure 1.
. The following graphs give the different shapes of the rational mapping (10), see Figure 1.
3. Method of Solution
In this section, we use the complex variable method to obtain the two complex functions (Goursat functions) ![]() and
and![]() . Moreover, the three stress components
. Moreover, the three stress components![]() ,
, ![]() and
and ![]() will be completely determined. The solution of Equation (9) is given by,
will be completely determined. The solution of Equation (9) is given by,
![]() (21)
(21)
By substituting Equation (19) in Equation (11) and using the definition of ![]() in polar coordinates the thermoelastic potential function takes the form,
in polar coordinates the thermoelastic potential function takes the form,
![]() (22)
(22)
Also, the stresses components can be adapted in the forms,
![]() (23)
(23)
![]() (24)
(24)
and,
![]() (25)
(25)
By using Equation (19) and Equation (20), Equations (21)-(23) becomes
![]() (26)
(26)
![]() (27)
(27)
and,
![]()
Figure 1. The different shapes of the rational mapping (10).
Figure 1. The different shapes of the rational mapping (10).
![]() (28)
(28)
where,
![]() (29)
(29)
After determining the Goursat functions the components of stress are completely determined.
Using Equation (8), the expression ![]() can be written in the form,
can be written in the form,
![]() (30)
(30)
where,
![]() (31)
(31)
![]() (32)
(32)
![]() ,
, ![]() and
and ![]() is a regular function for
is a regular function for![]() .
.
Using Equation (2) and Equation (3) in Equation (18), we get
![]() (33)
(33)
using Equation (29) in Equation (31), we have
![]() (34)
(34)
taking ![]() for generality, we get
for generality, we get
![]() (35)
(35)
where,
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
and,
![]() (39)
(39)
Assume that the function ![]() with its derivatives must satisfy Hölder condition. Our aim is to determine the functions
with its derivatives must satisfy Hölder condition. Our aim is to determine the functions ![]() and
and ![]() for the various boundary value problems. For this multiply both sides of Equ-
for the various boundary value problems. For this multiply both sides of Equ-
ation (35) by ![]() where
where ![]() is any point in the interior of
is any point in the interior of ![]() an integral over the circle, we obtain
an integral over the circle, we obtain
![]() (40)
(40)
using Equations (35)-(39) in Equation (40) then applying the properties of Cauchy integral to have
![]() (41)
(41)
where,
![]() . (42)
. (42)
The formula (41) represents the integro-differential equation of the second kind with Cauchy kernel.
To obtain the integral in terms of Equation (41) we use Equation (29) and then apply the residue theorem to have,
![]() (43)
(43)
where ![]() are complex constants which can be determined.
are complex constants which can be determined.
Also,
![]() (44)
(44)
So, Equation (41) reduce to,
![]() (45)
(45)
Differentiating Equation (45) with respect to ![]() and using the result in Equation (44), we obtain
and using the result in Equation (44), we obtain
![]() (46)
(46)
where,
![]() (47)
(47)
Hence, we have
![]() (48)
(48)
where,
![]() (49)
(49)
Also, from the boundary condition (35), ![]() can be determined in the form
can be determined in the form
![]() (50)
(50)
where,
![]() (51)
(51)
![]() (52)
(52)
![]() (53)
(53)
![]() (54)
(54)
![]() (55)
(55)
and,
![]() (56)
(56)
4. Special Cases
Now, we are in a position to consider several cases:
1) For![]() , we have the mapping
, we have the mapping ![]() discussed by Abdou and Kkhar El-din [9] , see Figure 2.
discussed by Abdou and Kkhar El-din [9] , see Figure 2.
2) For![]() , we have the mapping
, we have the mapping ![]() discussed by El-Sirafy and Abdou [15] , see Figure 3.
discussed by El-Sirafy and Abdou [15] , see Figure 3.
3) For![]() , we have the mapping
, we have the mapping![]() . The main reasons of interest in this
. The main reasons of interest in this
mapping is that the general shapes of the hypotrochids are curvilinear polygons, for ![]() see Muskhelishvili’s [27] . For
see Muskhelishvili’s [27] . For ![]() we have a curvilinear triangle see Abdou [28] . For
we have a curvilinear triangle see Abdou [28] . For ![]() a curvilinear square, see Abdou and Badr [29] , see Figure 4.
a curvilinear square, see Abdou and Badr [29] , see Figure 4.
5. Some Applications
In this section, we assume different values of the given function in the first or second fundamental boundary value problems. Then, we obtain the expression of Goursat functions. After that, the components of stresses can be calculated directly.
![]()
Figure 2. The different shapes of the rational mapping in (1).
Figure 2. The different shapes of the rational mapping in (1).
![]()
Figure 3. The different shapes of the rational mapping in (2).
Figure 3. The different shapes of the rational mapping in (2).
![]()
Figure 4. The different shapes of the rational mapping in (3).
Figure 4. The different shapes of the rational mapping in (3).
1. Application 1: When the curvilinear centre is not allowed to rotate. At![]() , the rigid curvilinear kernel is restrained in its original position by a couple which is not sufficient to rotate the kernel.
, the rigid curvilinear kernel is restrained in its original position by a couple which is not sufficient to rotate the kernel.
For![]() ,
,
Goursat’s functions in Equations (45) and (50) take the form
![]() (57)
(57)
![]() (58)
(58)
where,
![]() (59)
(59)
This application discusses the first fundamental boundary value problem of an infinite layer stretched at infinity by the application of a uniform tensile stress of intensity heat in the negative direction of y-axis. This layer is weakened by a curvilinear hole C which is free from stress.
For![]() ,
, ![]() ,
, ![]() ,
, ![]() , the stress components
, the stress components![]() ,
, ![]() and
and ![]() are obtained in large forms calculated by computer and illustrated in the following two cases:
are obtained in large forms calculated by computer and illustrated in the following two cases:
1) In the thermoelasticity layer, we have the following shapes for the stress components by using the substitutions![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , see Figure 5 and Figure 6.
, see Figure 5 and Figure 6.
2) When the study is in the normal layer, we have the following shapes for the stress components, see Figure 7 and Figure 8.
![]()
![]()
Figure 6. The ratio of vertical to horizontal stresses.
![]()
![]()
Figure 8. The ratio of vertical to horizontal stresses.
2. Application 2: Bi-axial tension
For![]() ,
,
Goursat’s functions in Equations (45) and (50) take the form
![]() (60)
(60)
![]() (61)
(61)
where,
![]() . (62)
. (62)
This application discusses the first fundamental boundary value problem of an infinite layer stretched at infinity by the application of a uniform tensile stress of intensity heat in the negative direction of y-axis. This layer is weakened by a curvilinear hole C which is free from stress.
For![]() ,
, ![]() ,
, ![]() ,
, ![]() , the stress components
, the stress components![]() ,
, ![]() and
and ![]() are obtained in large forms calculated by computer and illustrated in the following two cases:
are obtained in large forms calculated by computer and illustrated in the following two cases:
1) In the thermoelasticity layer, we have the following shapes for the stress components by using the substitutions![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , see Figure 9 and Figure 10.
, see Figure 9 and Figure 10.
![]()
![]()
Figure 10. The ratio of vertical to horizontal stresses.
2) When the study is in the normal layer, we have the following shapes for the stress components, see Figure 11 and Figure 12.
3. Application 3: When a couple with a given moment acting on the curvilinear hole and the stresses vanishing at infinity
For![]() ,
,
Goursat’s functions in Equations (45), (50) take the form
![]() (63)
(63)
![]() (64)
(64)
where,
![]() (65)
(65)
![]()
![]()
Figure 12. The ratio of vertical to horizontal stresses.
This application discusses the first fundamental boundary value problem of an infinite layer stretched at infinity by the application of a uniform tensile stress of intensity heat in the negative direction of y-axis. This layer is weakened by a curvilinear hole C which is free from stress.
For![]() ,
, ![]() ,
, ![]() ,
, ![]() , the stress components
, the stress components![]() ,
, ![]() and
and ![]() are obtained in large forms calculated by computer and illustrated in the following two cases:
are obtained in large forms calculated by computer and illustrated in the following two cases:
1) In the thermoelasticity layer, we have the following shapes for the stress components by using the substitutions![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , see Figure 13 and Figure 14.
, see Figure 13 and Figure 14.
2) When the study is in the normal layer, we have the following shapes for the stress components, see Figure 15 and Figure 16.
4. Application 4: The external force acts on the center of the curvilinear hole
For![]() , Then, Goursat, s functions in Equations (45), (50) take the form
, Then, Goursat, s functions in Equations (45), (50) take the form
![]() (66)
(66)
![]() (67)
(67)
where,
![]() (68)
(68)
![]()
![]()
Figure 14. The ratio of vertical to horizontal stresses.
This application discusses the first fundamental boundary value problem of an infinite layer stretched at infinity by the application of a uniform tensile stress of intensity heat in the negative direction of y-axis. This layer is weakened by a curvilinear hole C which is free from stress.
For![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , the stress components
, the stress components![]() ,
, ![]() and
and ![]() are obtained in large forms calculated by computer and illustrated in the following two cases:
are obtained in large forms calculated by computer and illustrated in the following two cases:
1) In the thermoelasticity layer, we have the following shapes for the stress components by using the substitutions![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , see Figure 17 and Figure 18.
, see Figure 17 and Figure 18.
2) When the study is in the normal layer, we have the following shapes for the stress components, see Figure 19 and Figure 20.
![]()
![]()
Figure 16. The ratio of vertical to horizontal stresses.
![]()
![]()
Figure 18. The ratio of vertical to horizontal stresses.
![]()
![]()
Figure 20. The ratio of vertical to horizontal stresses.
6. Conclusions
From the previous discussions we have the following results:
1) We find that the effect of heat is very clear; we find that the values of components stress are reduced with existence of heat, while at absence of heat we find the values of components of stresses are increasing.
2) With increasing angle and with absence![]() , we find that
, we find that
![]()
and,
![]()
3) With increasing angle and with existence![]() , we find that
, we find that
![]()
and,
![]()
4) The components of stresses effected are clear by increasing the values of![]() .
.