Performance Study of PID Controller and LQR Technique for Inverted Pendulum ()
1. Introduction
Inverted pendulum is one of the most difficult systems to control in the field of control engineering, because it is a non-linear as well as an unstable system. It provides a platform to test various control techniques and is used to simulate experiments such as walking robots, missile guidance and flying objects in space. To design a control system that keeps the pendulum balanced and tracks the cart to a commanded position, the conventional PID controller is still used in industries, because of its simple in control structure, not too expensive and elective for a linear system. The conventional PID controller can be used for virtually any process condition. This makes elimination the offset of the proportional mode possible and still provides fast response.
Generally, all systems are initially checked with conventional controllers including P, PI, and PID [1] since it is easy to develop and implement. Various methods are available for tuning these controllers. If the response is not satisfactory advanced, controllers are considered. When the system is non-linear and with significant delay, conventional controllers cannot give a satisfactory result [2] . LQR controller is a suitable alternative in such case. It can deal with non-linear systems efficiently. Pole placement methods like Ackerman’s formula are very popular in designing the state feedback gain K and hence to place the poles in desired locations [3] -[5] . But in these methods, we need to specify the desired poles to seek the SVFB gain. Also these methods are only applicable for single input systems. However, it is very inconvenient to specify all the closed loop poles and we would like to have a technique that works for many numbers of inputs. Due to these constrains, we make use of the theory of optimal control for the design of a better controller. Optimal controllers are designed in sense of using the least required control effort to maintain equilibrium [6] . Optimal control principle is inspired from naturally occurring systems which are optimal.
In Section 2, the problem is identified and defined. In Section 3, a detailed description about the experimental setup and system modelling is given. Section 4 describes about the designing of PID controller and LQR controller for the system. In Section 5, the simulation results are compared and Section 6 contains conclusion.
2. Problem Definition
The problem of controlling an inverted pendulum is to balance the pendulum in its upright position by moving the arm in opposite direction. The control output is limited by several constraints like the speed of motor controlling the arm. In this study, simulation of control in inverted pendulum system has been carried out using MATLAB and Simulink software.
3. Experimental Setup and Description
A Quanser rotary inverted pendulum which we used for modelling is shown in Figure 1. The inverted pendulum is hinged to its arm.
The horizontal movement of the arm and the pendulum vertical position angle are measured by optical encoder. The encoders produce 4096 pulses for revolution, which gives a very reasonable precision in measurement. The arm motion is actuated by a DC motor. The DC motor is controlling the rotary motion of the arm. Encoder is used to feedback the angular position of the pendulum to servo electronics to generate actuating signal. The controller circuits provide the controlling signal which then drives the arm through the servomotor. Rotary motion of the arm applies moments on the inverted pendulum and keeps the pendulum upright.
To model the inverted model we consider a much more simplified model as shown in Figure 2. The system dynamics can be studied from its energy relations [7]
![]()
Figure 1. The quaser inverted pendulum system.
The kinetic and potential energies are given by the following equations:
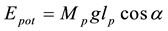 (1)
(1)
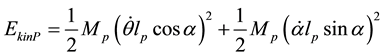 (2)
(2)
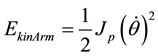 (3)
(3)
where Jp and Mp are arm inertia and pendulum mass respectively. Applying Lagrangian formula for the equations the state space model is obtained
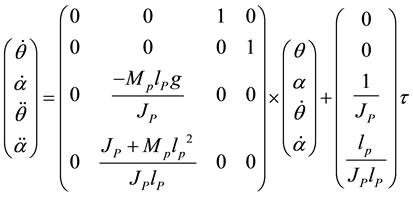 (4)
(4)
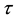 is the torque of the motor. Known constant values are given in the table 1 shown below.
is the torque of the motor. Known constant values are given in the table 1 shown below.
Substituting the known values in the equations we obtain the state space model of the system. The new state description of the system with voltage as input is given below:
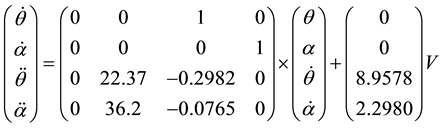 (5)
(5)
The transfer function model of the system obtained is given as:
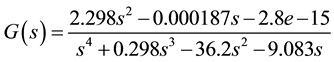 (6)
(6)
4. Controller Design
In this section, the LQR controller and PID controller design is discussed, also the controller design using MATLAB and Simulink is discussed in this section
4.1. PID controller Design
PID controller is the most widely used controllers for industrial applications [8] . PID controller design schemes are easy and robust in nature [9] . Defining “u” as the controller output, the final PID algorithm is of the form:
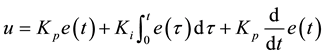
where Kp, Ki, Kd are proportional, integral and derivative gains respectively which are the tuning parameters used to design a PID controller. We used the transfer function model of the system to design a PID controller in Simulink. The Simulink model of the PID controller is given in Figure 3.
The values of tuning parameters Kp, Ki, and Kd are 516.35, 431.787 and 61.63 respectively.
4.2. LQR Controller Design
In this section, an LQR controller is developed for the inverted pendulum system. The LQR method uses the state feedback approach for controller design. As discussed, the system is expressed in state variable form as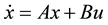 . We assume that all the states are measurable. The state variable feedback control can be found from the expression
. We assume that all the states are measurable. The state variable feedback control can be found from the expression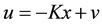 .
.
Using this control closed loop system becomes 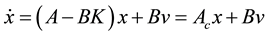 with Ac the closed loop plant matrix and v(t) the new command input. C and D matrices are not used in the SVFB design.
with Ac the closed loop plant matrix and v(t) the new command input. C and D matrices are not used in the SVFB design.
To design an optimal SVFB we may define a performance index.
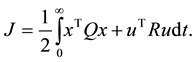
Substituting the SVFB we yields
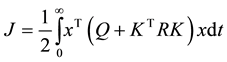
We assume v(t) as zero as our only concern is internal stability of the system. The objective is to select the K that minimizes the performance index J. Q and R must be selected to be positive semi-definite and positive definite in order to minimize J. The feedback gain matrix K in LOR is solved using the equation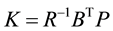 . To seek P we make use of a very important formula in modern control theory known as Algebraic Riccati Equation (ARE).
. To seek P we make use of a very important formula in modern control theory known as Algebraic Riccati Equation (ARE).
![]()
The design procedure for finding the feedback gain K for LQR can be formulated to 3 simple steps:
・ Select the design parameter matrices Q and R.
・ Find P by solving the ARE.
・ Find the state feedback matrix K using ![]()
![]()
Figure 3. Simulink model for PID control of Inverted pendulum.
The LQR guarantees pole placement and stability to the closed loop system as long as two LQR theorems [References] hold:
LQR theorem 1
Let the system (A, B) be reachable. Let R be positive definite and Q be positive definite. Then the closed loopsystem (A-BK) is asymptotically stable.
LQR theorem 2
Let the system (A, B) be stabilizable. Let R be positive definite, Q be positive semi definite, and ![]() be observable. Then the closed loop system (A-BK) is asymptotically stable. The simulink model for state feedback controller is shown in Figure 4.
be observable. Then the closed loop system (A-BK) is asymptotically stable. The simulink model for state feedback controller is shown in Figure 4.
The SVFB gain K is found using lqr command in Matlab and this gain is given in the Simulink model to obtain the outout.
The value of Q matrix which gave the best pole placement was [100 0 0 0; 0 1 0 0; 0 0 200 0; 0 0 0 1] and R matrix was selected as [1] .
The value of K derived is [−10.0000 719.0337 −17.8791 129.8297].
5. Results and Discussion
The PID and LQR controller performance for the system is simulated MATLAB Simulink. Q and R values are selected based on fine tuning by trial and error method. Responses of both the systems are studied with a square wave as input. The results of both the controllers are discussed in this section.
5.1. PID Controller Response
The response of the system with PID controller is shown in Figure 5. PID controller tuning for the proposed system model is showing only a very narrow region of stability. When the gains are increased, the system is settled fast but the overshoot is very high. When we reduce the overshoot by reducing the gain, the settling time has to pay the price. Figure 5 shows a reasonably good response obtained by tuning the PID controller.
5.2. LQR Response
The LQR controller gives a much stable and robust response for the system. The response of the system with LQR controller is given in Figure 6.
![]()
Figure 4. Simulink model for state feedback control.
![]()
Figure 5. Response of system with PID controller.
![]()
Figure 6. Regulatory response of PI controller and FLC.
There is a considerable reduction in overshoot and settling time with the LQR controller. The response is more stable and robust.