1. Introduction
Under the new regulations of Basel II and Solvency II, to be able to estimate their aggregate operational risk capital charge, many financial institutions have adopted a Loss Distribution Approach (LDA), consisting of a frequency and a severity distribution, based on its own internal losses. Yet, basing our models on historical losses only might not be the perfect robust approach since no future attention is being taken into consideration which can generate a biased capital charge, defined as the 0.01% quantile of the loss distribution, facing reality. On the other hand, adding scenario analysis given by the experts provide to some extent a future vision.
The main idea in this article is the following: A Bayesian inference approach offers a methodical concept that combines internal data with scenario analysis. We are searching first to integrate the information generated by the experts with our internal database; by working with conjugate family distributions, we determine a prior estimate. This estimate is then modified by integrating internal observations and experts’ opinion leading to a posterior estimate; risk measures are then calculated from this posterior knowledge. See [1] for more on the subject.
On the second half, we use Jeffreys non-informative prior and apply Monte Carlo Markov Chain with Metro- polis Hastings algorithm, thus removing the conjugate family restrictions and developing, as the article shows, a generalized application to set up a capital evaluation. For a good introduction to non-informative prior distribu- tions and MCMC see [2] .
Combining these different information sources for model estimation is certainly one of the main challenges in operational risk.
Modelling frequency and severity losses for estimating annual loss distribution, is known actuarial technique used to model, as well, solvency requirements in the insurance industry, see for e.g. [3] [4] . More literature on Operational Risk and Bayesian Inference techniques could be found in [5] - [8] .
2. Combining Two Data Sources: The Conjugate Prior
In our study, our data related to retail banking business line and external fraud event type is of size 279, collect- ed in $over 4 years. The data fits the Poission(5.8) as a frequency distribution, and 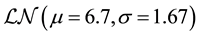 as the severity distribution.
as the severity distribution.
Applying Monte Carlo simulation [9] , with ,
, 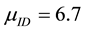 , and
, and , we obtained a Value-at- Risk of
, we obtained a Value-at- Risk of 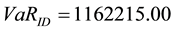 at 99.9%, using internal losses only.
at 99.9%, using internal losses only.
On the other hand, working with the scenario analysis, our experts gave us their assumptions for the frequency parameter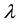 . As for the severity, our experts represent a histogram reflecting the probability that a loss is in an interval of losses (see Table 1 below).
. As for the severity, our experts represent a histogram reflecting the probability that a loss is in an interval of losses (see Table 1 below).
If we consider our severity distribution being Lognormal with paramters 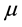 and
and , the objective is to find the parameters
, the objective is to find the parameters 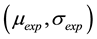 that adjust our histogram in a way to approach as much as possible the theoretical lognormal distribution. For this we can use chi-squared statistic that allows us to find
that adjust our histogram in a way to approach as much as possible the theoretical lognormal distribution. For this we can use chi-squared statistic that allows us to find 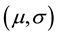 that minimize the chi-squared distance:
that minimize the chi-squared distance:
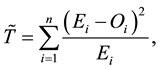
where 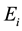 and
and 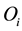 are respectively the empirical and theoretical probability.
are respectively the empirical and theoretical probability.
Our experts provided , and by applying chi-squared, we obtained our lognormal parameters:
, and by applying chi-squared, we obtained our lognormal parameters: 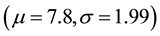 with the
with the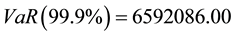 .
.
The high spread between the two VaR values, can cause a problem in allocating a non-biased capital require- ment. In the next sections, we will apply the Bayesian inference techniques, thus joining our internal observa- tions with the experts opinion.
2.1. Modelling Frequency Distribution
We are going to work with the Poisson and Lognormal distributions since they are the most used distributions in Operational Risk [10] .
Consider the annual number of events N for a risk in a bank modelled as a random variable from the Poisson distribution![]() , where
, where ![]() is considered as a random variable with the prior distribution
is considered as a random variable with the prior distribution![]() . So
. So
we have:![]() , and
, and ![]() has a prior density:
has a prior density:
![]()
As for the likelihood function, given the assumption that ![]() are independent, for
are independent, for![]() :
:
![]()
where n is the number of historical losses and ![]() is the number of losses in month i.
is the number of losses in month i.
Thus, the posterior density would be:![]() , but since
, but since ![]() plays the role of a nor- malizing constant,
plays the role of a nor- malizing constant, ![]() could be rewritten as:
could be rewritten as:
![]()
Which is![]() , i.e. the same as the prior distribution with
, i.e. the same as the prior distribution with ![]() and
and ![]()
So we have:
![]()
To apply this, and since the only unknown parameter is ![]() that is estimated by our experts with,
that is estimated by our experts with,![]() .
.
The experts may estimate the expected number of events, but cannot be certain of the estimate. Our experts specify ![]() and an uncertainty that the “true”
and an uncertainty that the “true” ![]() for next month is within the interval
for next month is within the interval ![]() with a probability
with a probability ![]() that
that![]() , then we obtain the below equations:
, then we obtain the below equations:
![]() (1)
(1)
![]() (2)
(2)
where ![]() is the
is the ![]() cumulative distribution function.
cumulative distribution function.
Solving the above equations would give us the prior distribution parameters![]() , and by using the formulas stated, we obtain:
, and by using the formulas stated, we obtain: ![]() and
and ![]() as our posterior parameters distri- bution. At the end, we calculate a
as our posterior parameters distri- bution. At the end, we calculate a ![]() using Monte Carlo simulation:
using Monte Carlo simulation:
• Using the estimated Posterior ![]() distribution, generate a value for
distribution, generate a value for![]() ;
;
• Generate n number of monthly loss regarding the frequency of loss distribution ![]()
• Generate n losses ![]() regarding the loss severity distribution
regarding the loss severity distribution![]() ;
;
• Repeat steps b and c for![]() . Summing all the generated
. Summing all the generated ![]() to obtain S which is the annual loss;
to obtain S which is the annual loss;
• Repeat steps a to d many times (in our case 105) to obtain the annual aggregate loss distribution.
• The VaR is calculated taking the 99.9th percentile of the aggregate loss distribution.
We notice that the Value-at-Risk is close to the VaR generated by the internal losses alone, since the only thing took as unknown was![]() , both parameters
, both parameters ![]() and
and ![]() are equal to
are equal to![]() .
.
2.2. Modelling Severity Distribution: ![]() with Unknown
with Unknown ![]()
Assume that the loss severity for a risk is modelled as a random variable from a lognormal distribution ![]() and we consider
and we consider ![]() as a prior distribution.
as a prior distribution.
So we have,
![]()
Taking![]() , we calculate the posterior distribution as previously by:
, we calculate the posterior distribution as previously by:
![]()
since we are using a conjugate prior distribution, we know that the posterior distribution will follow a Normal distribution with parameters ![]() where:
where:
![]()
By identification we obtain: ![]()
So, ![]() ,
, ![]() , with
, with ![]() and
and ![]()
Assuming that the loss severity for a risk is modelled as a random variable from a lognormal distribution ![]() and we consider
and we consider ![]() as a prior distribution.
as a prior distribution.
Since the only thing unknown is![]() , we already have
, we already have ![]() and
and![]() , and the experts gave us:
, and the experts gave us:
![]() (3)
(3)
![]() (4)
(4)
where ![]() is the cumulative distribution function of the standard normal distribution.
is the cumulative distribution function of the standard normal distribution.
Solving these two equations, we find that the prior distribution of ![]() is:
is: ![]()
Hence using the formulas stated above where, ![]() ,
, ![]() , and
, and![]() , with
, with ![]() is the total number of historical losses.
is the total number of historical losses.
We find out that the posterior distribution:![]() .
.
At the end, using the posterior ![]() distribution and Monte Carlo method, we calculate the 99.9% Value-at- Risk:
distribution and Monte Carlo method, we calculate the 99.9% Value-at- Risk:![]() .
.
The same analysis goes here as well, since the only unknown parameter is![]() ,
, ![]() , the VaR calculated will be closer to our Internal Data Value-at-Risk.
, the VaR calculated will be closer to our Internal Data Value-at-Risk.
2.3. Modelling Frequency and Severity Distributions
In the two previous subsections, we illustrated the case of modelling frequency and severity distributions with unknown ![]() that follows a
that follows a ![]() distribution and
distribution and ![]() that follows a
that follows a ![]() respectively.
respectively.
Joining these two distributions is relatively simple since we have the hypothesis of independence between frequency and severity, which allows us to estimate independently the two posterior distributions and estimate the parameters.
As so, we have already demonstrated the fact that our posterior density ![]() follows the
follows the ![]() distribution, with
distribution, with ![]() and
and ![]() and,
and, ![]() , with
, with![]() , with
, with![]() .
.
Since we have the hypothesis of independence between frequency and severity, which allows us to estimate independently the two posterior distributions, which have been already calculated for the parameter ![]() we took the gamma distribution and for the
we took the gamma distribution and for the ![]() parameter, the posterior distribution was normal with:
parameter, the posterior distribution was normal with:
![]()
![]()
By simulating those two laws using Monte Carlo simulation (cf. Section 2.1), we obtain a Value-at Risk of 1199000.00 using the estimated posterior Gamma and Normal distributions.
The result is interesting, since with two unknown parameters ![]() and
and![]() , the VaR is still closer to
, the VaR is still closer to![]() . This states that the parameter
. This states that the parameter ![]() is the key parameter in this application, as we are going to see throughout this article.
is the key parameter in this application, as we are going to see throughout this article.
The general case where all parameters are unknown will not be treated in this section since it is more complex to tackle it with the use of conjugate prior distributions.
2.4. Sensitivity Analysis
Working with this method, is generally simple since conjugate prior is involved, yet one of the main questions is how to ensure that experts opinion are consistent, relevant, and capture well the situation, which might in a way, cause a model error. In this work we did not take into consideration this aspect and the experts opinion were treated as correct. To improve our results, we can do a sensitivity test regarding our prior parameters. On the other hand, we only have the mean of the number of losses, given by our expert. So it appears difficult to obtain the distribution of ![]() with this only information. So in a way, we are immensely relying on our prior para- meters which in reality don’t give us a banking sense and are not easily comprehensive.
with this only information. So in a way, we are immensely relying on our prior para- meters which in reality don’t give us a banking sense and are not easily comprehensive.
We are going to test out prior parameters given by the experts and highlight the direct consequence on our Capital Required. To start with the first case, where we are working with unknown![]() ; our experts gave us a value of
; our experts gave us a value of ![]() and
and ![]() as seen in section 2.1, so taking into consideration a step of 0.035 for an interval
as seen in section 2.1, so taking into consideration a step of 0.035 for an interval ![]() and 0.1 for [6] [10] , respectively, we obtain the following VaR results (check Figure 1).
and 0.1 for [6] [10] , respectively, we obtain the following VaR results (check Figure 1).
As for the cases of unknown ![]() and unknown
and unknown![]() , we took an interval for
, we took an interval for ![]() and
and ![]() with a step of 0.1 (see Figure 2).
with a step of 0.1 (see Figure 2).
The following figures show the stability of our Value-at-Risk calculations regardless of all changes in our prior parameters![]() . Relying on the choice of our intervals, we notice that the boundaries of our VaR are in an acceptable range.
. Relying on the choice of our intervals, we notice that the boundaries of our VaR are in an acceptable range.
3. MCMC-Metropolis Hastings Algorithm
In this section, we will use a noninformative prior and more particularly the Jeffreys prior [11] , that attempts to represent a near-total absence of prior knowledge that is proportional to the square root of the determinant of the Fisher information:
![]()
![]()
![]()
Figure 1. Sensitivity for a0 and b0 respectively.
![]()
![]()
Figure 2. Sensitivity for μ0 and σ0 respectively.
where ![]()
Then we are going to apply an MCMC model to obtain a distribution for the parameters and generate our capital required at 99.9%. This will allow us to compare both methods’ results and develop a generalized application to set up our capital allocation, since no restrictions is made regarding the distributions. As for the parameter![]() , it will no longer be fixed as in the previous sections. For more details on the Jeffreys prior and MCMC-Metropolis Hastings algorithm check [12] .
, it will no longer be fixed as in the previous sections. For more details on the Jeffreys prior and MCMC-Metropolis Hastings algorithm check [12] .
3.1. MCMC with Poisson(l) Distribution
Assuming that the parameter ![]() is the only thing unknown, the Jeffreys prior distribution is:
is the only thing unknown, the Jeffreys prior distribution is: ![]() (see Appendix 5.1), thus finding the posterior distribution
(see Appendix 5.1), thus finding the posterior distribution ![]() with the use of experts Scenario Analysis and Internal Data would be:
with the use of experts Scenario Analysis and Internal Data would be:
![]()
So by applying Metropolis Hastings algorithm, (check Appendix 5.2.1 for full support on detailed algorithm), with the objective density:
![]()
and with a uniform proposal density: ![]() , we obtain the parameter
, we obtain the parameter ![]() distribution see Figure 3.
distribution see Figure 3.
We have removed the first 3000 iterations so that the chain is stationary (burn-in iterations effect), [13] . We
obtain a 99.9% Value-at-Risk of 1000527.00
The result is close to the VaR considered with the use of conjugate family.
3.2. MCMC with ![]() Distribution with Unknown
Distribution with Unknown ![]()
Assuming that the parameters ![]() and
and ![]() are the only things unknown, we will treat them independently and since the Poisson(l) case has already been treated, the Jeffreys prior distribution for
are the only things unknown, we will treat them independently and since the Poisson(l) case has already been treated, the Jeffreys prior distribution for ![]() is:
is: ![]()
(see Appendix 5.1), thus finding the posterior distribution ![]() with the use of experts Scenario Analysis and Internal Data would be:
with the use of experts Scenario Analysis and Internal Data would be:
![]()
So by applying Metropolis Hastings algorithm, (check Appendix 5.2 for full support on detailed algorithm), with the objective density:
![]()
and with a uniform proposal density:![]() , we obtain the parameter
, we obtain the parameter ![]() distribution see Figure 4.
distribution see Figure 4.
We obtain a Value-at-Risk of 1167060.00.
Comparing this to the same case generated with conjugate prior, we can check the closeness of both values.
In the next subsection, we will tackle the general case, where all parameters are unknown, this case was not treated with conjugate prior distributions since it would be more complicated.
3.3. MCMC: The General Case
We are going to assume the general case, where all the parameters are unknown![]() ,
, ![]() and
and![]() , we will treat them independently and since the Poisson(l) case has already been employed, the Jeffreys prior distribution for
, we will treat them independently and since the Poisson(l) case has already been employed, the Jeffreys prior distribution for
![]() is:
is: ![]() (cf. Appendix 5.1), thus finding the posterior distribution
(cf. Appendix 5.1), thus finding the posterior distribution ![]() with the use of experts Scenario Analysis and Internal Data would be:
with the use of experts Scenario Analysis and Internal Data would be:
![]()
So by applying Metropolis Hastings algorithm, (check Appendix 5.2.3 for full support on detailed algorithm), with the objective density:
![]()
and with a uniform proposal density: ![]() and
and ![]() for
for ![]() and
and ![]() respectively, we obtain the parameters
respectively, we obtain the parameters ![]() and
and ![]() distributions, illustrated in Figure 5.
distributions, illustrated in Figure 5.
We have removed as well, the first 3000 iterations so that the chain is stationary (burn-in iteration effect). We obtain a Value-at-Risk of 3061151.00.
The general case clearly generates a good combination between internal data and experts’ opinion with a capital requirement of 3,061,151$.
3.4. Confidence Interval Calculation
To recapitulate on all the calculations, Table 2 summarizes all Value-at-Risk generated. As for the calculation of the confidence interval, since we are working with order statistics, the interval ![]() would cover our quantile
would cover our quantile ![]() with a 95% probability that depends on the lower bound l, upper bound u, number of steps n and confidence level p.
with a 95% probability that depends on the lower bound l, upper bound u, number of steps n and confidence level p.
In our calculations, we took![]() ,
, ![]() and our integers
and our integers![]() , were constructed using the normal approximation
, were constructed using the normal approximation ![]() to the binomial distribution
to the binomial distribution![]() , (since n is large). Then a simple linear interpolation has been made to obtain the values of
, (since n is large). Then a simple linear interpolation has been made to obtain the values of![]() , (see [14] , pp. 183-186), for more details and demonstrations.
, (see [14] , pp. 183-186), for more details and demonstrations.
Table 2 clearly shows the helpful use of the Bayesian inference techniques. The results of both methods are close and comparable; though conjugate prior is simple but the distributions are restricted to the conjugate family, yet with the Jeffreys non-informative prior and MCMC-Metropolis Hastings algorithm, we will have a wider options and generate a good combination between internal data and experts’ opinion.
In addition, we are going to use the Monte Carlo confidence intervals approach [15] in order to compare it with the previous approach and ensure the similarities.
Consider a parameter X with its consistent estimator Y, with cumulative distribution function ![]() generated by some process which can be simulated. Number of simulations n and y values are independently generated and then ordered from largest to smallest. An approximate
generated by some process which can be simulated. Number of simulations n and y values are independently generated and then ordered from largest to smallest. An approximate ![]() confidence level for X is
confidence level for X is
given by ![]() where j and k represent respectfully the lower and upper bound of the interval and they are set as:
where j and k represent respectfully the lower and upper bound of the interval and they are set as: ![]() and
and![]() . Usually j and k will not be integer; therefore we can simply round
. Usually j and k will not be integer; therefore we can simply round
it to the nearest integer values or even use linear interpolation.
![]()
Figure 5. MCMC for the parameters μ and σ.
![]()
Table 2. Value at risk and confidence intervals for all cases treated.
We seek to calculate![]() , this may be found, using a conventional
, this may be found, using a conventional ![]() confidence level, by solving:
confidence level, by solving: ![]() and
and![]() .
.
The actual confidence level has a beta distribution with parameters ![]() and
and![]() , this is concluded when percentiles of the distribution
, this is concluded when percentiles of the distribution ![]() are estimated by simulation.
are estimated by simulation.
Respecting that B has a beta distribution, ![]() and
and ![]()
In our case, by using the confidence level of 99.9% and by applying the previous calculations we have obtain- ed an approximation 95% interval for actual confidence level with![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() and by moving 1.96 standard errors in either direction from the estimate we obtain our confidence interval:
and by moving 1.96 standard errors in either direction from the estimate we obtain our confidence interval:![]() , which is very
, which is very
close to the previous interval calculation in Table 2.
Furthermore, Figure 6 and Figure 7 illustrate the calculation of our Value-at-Risk for different confidence level. It clearly shows the presence of the general case, between both Internal and Scenario Analysis curves. On the other hand, the conjugate prior Figure 7, regarding all 3 unknown variables, point out the closeness of the curves which add to our previous analysis that ![]() is our key parameter.
is our key parameter.
We have to note as well, that the concept of Scenario Analysis with the expert opinion should deserve more clarification. Roughly speaking, when we refer to experts judgments, we express the idea that banks’ experts and experienced managers have some reliable intuitions on the riskiness of their business and that these intuitions are not entirely reflected in the bank’s historical, internal data. In our case, experts’ intuitions were directly plugged into severity and frequency estimations through building a loss histogram.
![]() (a)
(a)![]() (b)
(b)
Figure 6. Different VaR calculation for all MCMC cases, internal data and scenario analysis.
![]()
Figure 7. Different VaR calculation for all conjugate prior cases.
3.5. Bayesian Approach Reviewed
In this part, we are going to replace the experts opinions, by assuming that the experts’ parameters are set using the Basel II standardized approach calculation. Hence, the experts opinion is questionable in the meaning of when it’s used, we shift into the Markovian process which can cause problems.
3.6. Standardized Approach Reviewed
In the Standardized Approach (SA), banks’ activities are divided into 8 business lines [16] [17] : corporate finance, trading & sales, retail banking, commercial banking, payment & settlements, agency services, asset management, and retail brokerage. Within each business line, there is a specified general indicator that reflects the size of the banks’ activities in that area. The capital charge for each business line is calculated by multiply- ing gross income by a factor ![]() assigned to a particular business line (Table 3).
assigned to a particular business line (Table 3).
The total capital charge is calculated as a three year average over all positive gross income (GI) as follows:
![]()
Hence, the application of the Standardized Approach generates a capital requirement of ![]()
Numerical Results for Expert Opinion Treated as SA
Setting the parameters to give us the same Standardized approach capital requirement and treating them as the expert parameters gave us:![]() ,
, ![]() and
and![]() .
.
We note that the Standardized approach from Basel II is the one to rely on when it comes to calculate the VaR with it’s confidence interval. It is interesting to compare both results in Table 2 and Table 4 where we notice
![]()
Table 3. Business lines and the beta factors.
![]()
Table 4. Value at risk and confidence intervals for all cases treated.
that the VaR results in the cases of bayesian unknown![]() , unknown
, unknown ![]() and unknown
and unknown![]() ,
, ![]() are very close to the result in the Aggregate case. As for the MCMC approach where experts opinion are respected, in the case of unknown
are very close to the result in the Aggregate case. As for the MCMC approach where experts opinion are respected, in the case of unknown![]() ,
, ![]() and
and ![]() the results are close to the Scenario Analysis VaR. We conclude that, the expert opinion used parameters can be uncertain and cause an issue because it can lead to a disruption in the Markovian process. Combining these different data sources, highlights the importance of experts opinion coherence which generate an estimation risk that affects our capital required calculation.
the results are close to the Scenario Analysis VaR. We conclude that, the expert opinion used parameters can be uncertain and cause an issue because it can lead to a disruption in the Markovian process. Combining these different data sources, highlights the importance of experts opinion coherence which generate an estimation risk that affects our capital required calculation.
4. Conclusions
Using the information given by the experts, we were able to determine all the parameters of our prior distri- bution, leading to the posterior distributions with the use of internal data, which allowed us to compute our own capital requirement. This approach offers a major simplicity in its application through the employment of the conjugate distributions. Therefore, allowing us to obtain explicit formulas to calculate our posterior parameters. Yet, the appliance of this approach could not be perfected since it's restricted to the conjugate family.
On the other hand, Jeffreys prior with MCMC-Metropolis Hastings algorithm provided us with wider options and generated a satisfactory result regarding all three unknown variables![]() ,
, ![]() and
and![]() , with the only dif- ference of using complex methods. Taking
, with the only dif- ference of using complex methods. Taking ![]() unknown as well, was very essential in reflecting the credibility of estimating our capital requirement.
unknown as well, was very essential in reflecting the credibility of estimating our capital requirement.
Yet, treating the experts outputs, the same as Basel’s operational risk Standardized approach, illustrated the necessity of calling attention to the judgments given. In our application, judgments were needed to make sensi- ble choices but these choices will influence the results. Understanding this influence, should be an important aspect of capital calculations, since it created an estimation risk that has highly influenced our capital require- ment [18] , for the judgment under uncertainty. Moreover, we did not take into consideration external data, which might be interesting to elaborate and apply in practice, more on this subject could be found in [19] .
5. Appendix
5.1. Jeffreys Prior Distribution
Jeffreys prior attempts to represent a near-total absence of prior knowledge that is proportional to the square root of the determinant of the Fisher information:
![]()
where ![]()
5.1.1. Jeffreys Prior for Poisson(l) and Lognormal(m, s) Distributions
Let![]() , the poisson density function is:
, the poisson density function is: ![]() with,
with,
![]()
and consequently, ![]()
Let![]() , with
, with ![]()
Hence, by letting ![]() and calculating the corresponding partial derivatives to
and calculating the corresponding partial derivatives to ![]() we obtain:
we obtain:
![]()
As a consequence, ![]() and
and ![]()
5.2. MCMC Metropolis-Hastings Algorithm
5.2.1. Applying MCMC with Metropolis Hastings Algorithm for l
• Initialize ![]()
• Update from ![]() to
to ![]()
![]() by
by
- Generating ![]()
- Define ![]()
- Generate ![]()
- If![]() ,
, ![]() , else
, else ![]()
• Remove the first ![]() iterations, so that the chain is stationary (burn-in effect).
iterations, so that the chain is stationary (burn-in effect).
5.2.2. Applying MCMC with Metropolis-Hastings Algorithm for m
• Initialize ![]()
• Update from ![]() to
to ![]()
![]() by
by
- Generating ![]()
- Define ![]()
- Generate ![]()
- If![]() ,
, ![]() , else
, else ![]()
• Remove the first 3000 iterations, so that the chain is stationary (burn-in effect).
5.2.3. Applying MCMC with Metropolis-Hastings Algorithm for w = (m,s)
• Initialize ![]() and
and ![]()
• Update from ![]() to
to ![]() and
and ![]() to
to![]() ,
, ![]() by
by
- Generating ![]() and
and ![]()
- Define ![]()
- Generate ![]()
- If![]() ,
, ![]() and
and ![]() else
else ![]() and
and ![]()
• Remove the first 3000 iterations from both distributions, so that the chains is stationary (burn-in effect).