Quantum Corrections on Tunneling Radiation by the Generalized Uncertainty Principle ()
1. Introduction
In 1974, Hawking pointed out that Hawking radiation could be regarded as a process of tunneling where the vacuum fluctuation is caused at the event horizon of black holes [1] [2] . Then, the Hawking radiation attracted more and more attentions of theoretical physicists. Considering the relativistic quantum mechanics, T. Dmour and R. Ruffini studied the Hawking radiation again in 1976, and later, this method was greatly developed by Zhao et al. [3] . Soon, with the development of the quantum field theory and quantum statistics, Sannan et al. obtained the pure thermal spectrum from black holes. Especially in 2000, Parikh et al. proposed a semi-classical quantum tunneling method to study the Hawking radiation of black holes [4] [5] , and then many effects worked on it. In this method, the WKB approximation played an important role in the calculation of the Hawking temperature. Later, using this method, the higher dimensional black hole, the dynamical black hole and the de Sitter black hole have been studied, and some important results were obtained. In 2007, Kerner and Mann studied the Dirac equation with this method, the Hawking temperature of 1/2-spin particles was obtained [6] and the tunneling rate and the Hawking temperature were obtained. After that, many effects on the Hawking radiation of 1/2-spin particles and scalar particles have been done [7] -[12] . Now, the quantum tunneling theory has a more widespread application and development on the research of the Hawking radiation.
In 2000, the development of quantum gravitational theory came into a period of rapid development. And the significant representative was the supergravity theory and loop quantum gravity theory. More and more evidences implied that the generalized uncertainty principle (GUP) could describe the minimum measurable length [13] -[17] , based on the modified fundamental commutation relation [18]
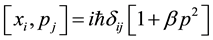 (1)
(1)
The expression of GUP is derived as [19]
 (2)
(2)
where, 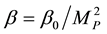 ,
, 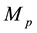 is the Planck mass,
is the Planck mass, 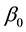 is a dimensionless parameter and
is a dimensionless parameter and ,
, 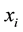 and
and  can be found in the reference [19] ,
can be found in the reference [19] ,
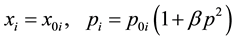 (3)
(3)
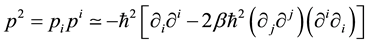 (4)
(4)
Also, many other various modifications are referred to [18] - [25] . In curved spacetime, those modifications are widely used to discuss black hole models. Through the quantum tunneling method and the GUP, the tunneling behavior of the scalar particle of Schwarzschild black hole has been studied by K. Nozari et al. [20] and many other studies of the tunneling behavior has been discussed in [21] -[24] . Lots of evidences indicate that the quantum gravity research has the important significance to the Hawking radiation.
The aim of this paper is to study the tunneling radiation of scalar particles in the GHS black hole with the Klein-Gordon equation near the horizon. The rest of this paper proceeds as follow: Section 2 modifies the Klein- Gordon equation; Section 3 studies the Hawking radiation of the GHS black hole with the Klein-Gordon equation; Section 4 is only a conclusion.
2. The Corrected Klein-Gordon Equation
In this section, we will discuss the modified Klein-Gordon equation by the quantum gravity in carved spacetime. In 1995, Kempf put forward the GUP, and the expression can be found in Equation (2). In Equation (3), the canonical commutation relations which express as 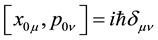 should be satisfied. The four-dimensional Klein-Gordon equation without the electromagnetic field is given by the following form [25] ,
should be satisfied. The four-dimensional Klein-Gordon equation without the electromagnetic field is given by the following form [25] ,
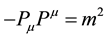 (5)
(5)
To studied the effect which the quantum gravity have on the Klein-Gordon equation, we expand the Klein- Gordon equation as two parts, the left hand is relate to the square of energy, and the right hand is relate to the square of coordinate. So we rewrite this equation as,
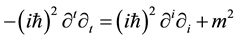 (6)
(6)
In reference [19] , the generalized expression of energy can be rewritten as,
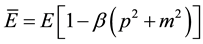 (7)
(7)
In above equation, the mass-energy shell condition 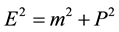 was considered. Therefore, after we substituted Equations (3) (4) (7) into Klein-Gordon equation, the modified Klein-Gordon equation are given as [25] ,
was considered. Therefore, after we substituted Equations (3) (4) (7) into Klein-Gordon equation, the modified Klein-Gordon equation are given as [25] ,
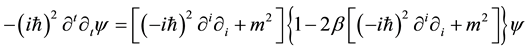 (8)
(8)
Carefully analysis on the modified Klein-Gordon equation, it is obvious for us that the quantum gravity has an important influence on the dynamic behavior of scalar particles. In the following section, we will aim at the tunneling behavior of scalar particles of the GHS black hole with the Klein-Gordon equation.
3. The Tunneling Radiation of the GHS Black Hole
In this section, we are devoted to study tunneling radiation of scalar particles across the horizon of the GHS black hole in string theory by using modified Klein-Gordon equation. The GHS black hole is a member of a family of solutions to low energy string theory, the action can be written as,
![]() (9)
(9)
where ![]() is the dilaton field,
is the dilaton field, ![]() is the Maxwell field. So the metric of the GHS black hole in the string frame is,
is the Maxwell field. So the metric of the GHS black hole in the string frame is,
![]() (10)
(10)
Here,
![]() (11)
(11)
![]() (12)
(12)
And,
![]() (13)
(13)
The symbol ![]() is the asymptotic constant value of the dilaton field, and the expression of event horizon of the GHS black hole is
is the asymptotic constant value of the dilaton field, and the expression of event horizon of the GHS black hole is![]() . Then, we will investigate the tunneling radiation of the GHS black hole near the event horizon with the modified Klein-Gordon equation. First, we employ the wave function of the scalar particle as
. Then, we will investigate the tunneling radiation of the GHS black hole near the event horizon with the modified Klein-Gordon equation. First, we employ the wave function of the scalar particle as
![]() (14)
(14)
where ![]() is the action of the scalar particles, and it is the function of
is the action of the scalar particles, and it is the function of![]() . Substituting the wave function into the modified Klein-Gordon equation,
. Substituting the wave function into the modified Klein-Gordon equation,
![]() (15)
(15)
The equation of motion of scalar particles is obtained,
![]() (16)
(16)
For the convenience of later calculation, the higher order terms of ![]() in above equation were neglected. Then, the standard separation of variables are taken into account [25] ,
in above equation were neglected. Then, the standard separation of variables are taken into account [25] ,
![]() (17)
(17)
Here, ![]() is the energy of the outgoing scalar particles,
is the energy of the outgoing scalar particles, ![]() is the radial component of the action. Substituting Equation (17) into Equation (16),
is the radial component of the action. Substituting Equation (17) into Equation (16),
![]() (18)
(18)
And after we considered the tunneling behavior is the radial, so the following form is obtained,
![]() (19)
(19)
Here, ![]() is a constant and its value can be take as zero. Therefore, the Equation (18) can be simplified as,
is a constant and its value can be take as zero. Therefore, the Equation (18) can be simplified as,
![]() (20)
(20)
where,
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
Taking conditions ![]() and
and ![]() into account. So,
into account. So,
![]() (24)
(24)
It is easy for us to calculate the roots of the above equation, after we substituted Equations (11), (12) into Equation (24), so the solution of this quartic equation at the horizon is,
![]() (25)
(25)
With the path integral, substituting the metric of the GHS black hole into the above equation, we can finally find that the value of the GHS black hole,
![]() (26)
(26)
And, ± can be related to outgoing/ingoing particles of the GHS black hole, the symbol ![]() can be express as,
can be express as,
![]() (27)
(27)
The relation between the tunneling rate and the action is,
![]() (28)
(28)
So the corrected tunneling rate of the GHS black hole near the event horizon can be express as,
![]() (29)
(29)
Therefore, it is easy for us to obtain the corrected Hawking temperature of the GHS black hole near the event horizon,
![]() (30)
(30)
Neglecting the higher order terms of![]() , the corrected Hawking temperature can be rewritten as,
, the corrected Hawking temperature can be rewritten as,
![]() (31)
(31)
And,
![]() (32)
(32)
The corrected Hawking temperature and corrected tunneling rate of GHS black hole are obtained in Equations (29)-(32). It is obvious for us to see that the corrected Hawking temperature is not related to the metric of the black hole, but related to the mass and energy of the outgoing particles. So, the quantum gravity has an important influence on the Hawking radiation of the GHS black hole. Carefully analysis on results in Equation (31), it gives us the information that the quantum correction slows down the increase of temperature during the tunneling radiation, so the Hawking radiation will stop at some particular temperature. In this way, it imply us that residuum of GHS black hole is left certainly. Now, let’s focus on the residuum of black holes. Considering the massless particle and the condition![]() ,
, ![]() , the Hawking temperature stops increasing when,
, the Hawking temperature stops increasing when,
![]() (33)
(33)
The residue mass and the upper limit value of temperature in black hole can be express as,
![]() (34)
(34)
![]() (35)
(35)
Here, ![]() ,
, ![]() ,
, ![]() ,
, ![]() is the Planck mass. In this way, we neglect the higher order terms of
is the Planck mass. In this way, we neglect the higher order terms of![]() . So, Equation (34) is the expression of the residuum in black hole.
. So, Equation (34) is the expression of the residuum in black hole.
4. Conclusions
In this paper, we aim at the quantum tunneling radiation of scalar particles of the GHS black hole with the consideration of quantum gravity. The results in Equation (31) imply that the tunneling radiation is not only related to the mass of the GHS black hole, but also related to the mass and energy of the outgoing particle. So we can realize that this correction on the Hawking radiation is very important, and can not be neglected. According to the Equation (31), it indicates that parameters ![]() slow down the increase of temperature during the tunneling radiation, and the Hawking radiation will stop at some particular temperature. According to the careful calculation, the residue mass and the upper limit value of temperature in black hole can be obtained which are
slow down the increase of temperature during the tunneling radiation, and the Hawking radiation will stop at some particular temperature. According to the careful calculation, the residue mass and the upper limit value of temperature in black hole can be obtained which are ![]() and
and![]() . It is precisely because of the residue mass of the black hole that we find that the singularity question of the black hole is avoided. On the other hand, the Hawking radiation is replenished once again by this conclusion.
. It is precisely because of the residue mass of the black hole that we find that the singularity question of the black hole is avoided. On the other hand, the Hawking radiation is replenished once again by this conclusion.
Now, the cosmic scale and microscale are all important in the research of the physics fields. The conclusion in this paper supports this viewpoint, and the present studies indicate that the quantum gravity is worth studying. Until now, it has attracted much more attention of theory physicists and become one of the most important issues in the astronomy and theoretical physics. In the future work, we will try more and more efforts on this issue.
Acknowledgements
Major Project of Education Department in Sichuan Province, No: 15ZA0325.
NOTES
*Corresponding author.