Classical Chaos on Double Nonlinear Resonances in Diatomic Molecules ()
1. Introduction
Beside the clear importance of the study of diatomic molecules [1] and [2] , one of the actual interests in classical chaotic behavior of diatomic molecules, due to double nonlinear resonances, is the connection with its associated quantum dynamics [3] - [5] . For a quantum system associated to non chaotic classical one, it is mostly believed that classical dynamical behavior must occur for large quantum numbers or high value of the action variable [6] [7] . However, for the quantum counter part of a chaotic classical system the situation can be very different [8] [9] , where the associated action or quantum number when chaos has his manifestation on classical system is small [10] [11] . In this case the “quantum manifestation of chaos” is rather a subtle matter. These studies have been done so far using the coordinates of angle-action in the Hamiltonian formalism of diatomic molecule system [12] , where a somewhat artificial nonlinear action term is introduced on the system [10] , keeping the angular momentum at zero approximation. However, the nonlinear terms can be also introduced naturally by taking higher terms on the approximation on the potential energy for large amplitude of oscillations of the system, and by doing the same type of approximation with the angular momentum of the systems. On the other hand, when nonlinear resonances appear on a classical system, chaotic behavior of the system is determinated by Chririkov’s criteria of overlapping resonances [13] [14] . However, this criterion is not convenient for our study since one of the resonances is weak (small stability region in phase space) and the other is very strong (large stability region in phase space). To determine the chaotic behavior on the system we use Lyapunov exponent, separation of two nearby trajectories, and Fourier transformation of the time evolution of the system. In this study we show that it is possible to observe other types of chaotic behavior where chaos can depend on conditions around the critical points (initial conditions chaotic behavior), and we proceed in the following way: we establish the evolution equations of a diatomic molecule within a circular resonant electric field for large amplitude oscillations, making up to fourth order of approximation on the potential interaction between atoms and the angular momentum of the system. We solve numerically the resulting Hamiltonian equations and calculate the Lyapunov, distance between two nearby trajectories, and Fourier transformation to determine whether or not the trajectory is chaotic or not [15] . For one selected diatomic molecule, we choose initial conditions near the weak and the strong critical points and increase the magnitude of the electric field until the chaotic behavior appears on each case (experimentally, this chaotic behavior can be measured by electron diffraction technique [16] ). Finally, the same study is done in other diatomic molecules.
2. Equation of Motion
The study of diatomic molecule is a typical two bodies problem with radial force as shown in Figure 1, where 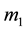 and
and 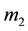 are the masses of the two atoms,
are the masses of the two atoms, 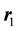 and
and 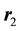 are their position,
are their position, 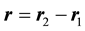 is the relative coordi- nate, and
is the relative coordi- nate, and 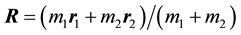 is the center of mass coordinate. It is well known that with these last two coordinates, the equations of motion are reduced from 6-D to 3-D problem, and the equations are written as
is the center of mass coordinate. It is well known that with these last two coordinates, the equations of motion are reduced from 6-D to 3-D problem, and the equations are written as
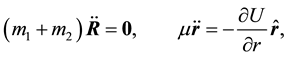 (1)
(1)
where 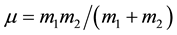 is the reduced mass of the system, and
is the reduced mass of the system, and 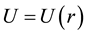 is the potential due to the central force between de molecules.
is the potential due to the central force between de molecules.
Due to the symmetry under rotation of the system, the relative motion is reduced to 1-D problem and its
![]()
Figure 1. Two bodies central force case.
equation is given in spherical coordinates by
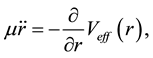 (2)
(2)
where the effective potential is
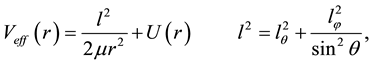 (3)
(3)
being l the angular moment of the system with
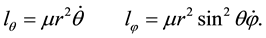 (4)
(4)
The constant of motion (energy) associated to this system is
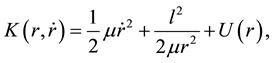 (5)
(5)
and its Lagrangian is
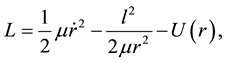 (6)
(6)
or
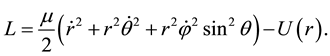 (7)
(7)
Therefore, its Hamiltonian is
![]() (8)
(8)
3. Approximation on Potential and Angular Moment
Let ![]() be the minimum of the effective potential
be the minimum of the effective potential![]() , and let us expand the functions
, and let us expand the functions ![]() and
and ![]() around this point. Defining the variable
around this point. Defining the variable ![]() as
as ![]() (with
(with![]() ), it follows that
), it follows that
![]() (9)
(9)
and
![]() (10)
(10)
Since one has that![]() , let us define ωo (the natural frequency of oscillation of the molecule) from the
, let us define ωo (the natural frequency of oscillation of the molecule) from the
relation![]() . So, our Hamiltonian a fourth order is
. So, our Hamiltonian a fourth order is
![]() (11)
(11)
where one has that![]() .
.
The potential associated to the molecular interaction ![]() is just the Morse’s potential [17] ,
is just the Morse’s potential [17] ,
![]() (12)
(12)
where D, ![]() , and
, and ![]() are parameter determined for each molecule. The parameter D represents the disso- ciation energy of the molecule and the deep of the potential,
are parameter determined for each molecule. The parameter D represents the disso- ciation energy of the molecule and the deep of the potential, ![]() is the minimum of this potential and the equilibrium distance of the atoms, and
is the minimum of this potential and the equilibrium distance of the atoms, and ![]() is related with the width of the potential, and it follows that
is related with the width of the potential, and it follows that
![]() (13)
(13)
Then, the above Hamiltonian can be written of the form
![]() (14)
(14)
where ![]() and
and ![]() are defined as
are defined as
![]() (15)
(15)
and
![]() (16)
(16)
Let us recall that ![]() can be written in terms of the generalized linear momenta as
can be written in terms of the generalized linear momenta as
![]() (17)
(17)
Then, Hamilton’s equations of motion are
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
From the last equation one has that![]() , and the total angular momentum l is another constant of motion. Thus, by choosing the motion at
, and the total angular momentum l is another constant of motion. Thus, by choosing the motion at![]() , the dynamical system is reduced to the following two dimen- sional autonomous system
, the dynamical system is reduced to the following two dimen- sional autonomous system
![]() (24)
(24)
![]() (25)
(25)
The set of critical points for this system, ![]() , is given by
, is given by
![]() (26)
(26)
that is, the critical points are located over the ![]() -axis, and they are determined by the real roots of a third order polynomial, which means that one will have one or three real roots, depending on the values of the coefficients. As it is known [18] [19] , the nature of this critical points is determined by the trace and determinate of the Jacobian matrix,
-axis, and they are determined by the real roots of a third order polynomial, which means that one will have one or three real roots, depending on the values of the coefficients. As it is known [18] [19] , the nature of this critical points is determined by the trace and determinate of the Jacobian matrix,
![]()
Since one has that![]() , this implies that the critical points are center points (if
, this implies that the critical points are center points (if![]() ) or
) or
hyperbolic points(if![]() ). For example, for the BeO molecule (Berilium Oxide), the parameter are (in MKS units)
). For example, for the BeO molecule (Berilium Oxide), the parameter are (in MKS units)
![]() (27)
(27)
and its characteristic frequency is
![]() (28)
(28)
The set critical points is![]() , where
, where ![]() are given by
are given by
![]() (29)
(29)
and one has
![]() (30)
(30)
Therefore, ![]() and
and ![]() represent centers, and
represent centers, and ![]() represents an hyperbolic point. Some tra- jectories on the phase space
represents an hyperbolic point. Some tra- jectories on the phase space ![]() can be seen in Figure 2 for this molecule, obtained numerically by solving (24) and (25). These trajectories represent the regular behavior of the system (Lyapunov exponent is negative, two nearby trajectories remain always nearby, Fourier transformation of any of these trajectories has only peaks).
can be seen in Figure 2 for this molecule, obtained numerically by solving (24) and (25). These trajectories represent the regular behavior of the system (Lyapunov exponent is negative, two nearby trajectories remain always nearby, Fourier transformation of any of these trajectories has only peaks).
The values ![]() for some diatomic molecules are shown on the table of appendix A, where the Morse’s parameters associated to each molecule were taken from [17] .
for some diatomic molecules are shown on the table of appendix A, where the Morse’s parameters associated to each molecule were taken from [17] .
4. Adding Electric Field and Non Autonomous Dynamical System
Diatomic molecules with a dipolar moment ![]() can interact with an external electric field. The dipole electric
can interact with an external electric field. The dipole electric
![]()
Figure 2. Trajectories on the phase space for the molecule BeO.
moment is just the charge times the distance between atoms, ![]() , where in spherical coordinates
, where in spherical coordinates ![]() . If the electric field E is chosen of the form
. If the electric field E is chosen of the form![]() , the energy of interaction is
, the energy of interaction is![]() , and the Hamiltonian of interaction is then
, and the Hamiltonian of interaction is then
![]() (31)
(31)
Let ![]() be the average of dipolar moment over the angles and time,
be the average of dipolar moment over the angles and time, ![]() , and let us absorb the constant term
, and let us absorb the constant term ![]() on the definition of the Hamiltonian. Thus, one consider the Hamiltonian of interaction as
on the definition of the Hamiltonian. Thus, one consider the Hamiltonian of interaction as
![]() (32)
(32)
In this way, using (14), (15) and (16), the full Hamiltonian is
![]() (33)
(33)
and the equations of motion are now
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
By choosing the study of motion at ![]() as before, one obtains that
as before, one obtains that![]() , and system is reduced to a four dimensional non autonomous system
, and system is reduced to a four dimensional non autonomous system
![]() (40)
(40)
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
These equation are solved numerically to find the dynamical behavior of the system. What we are interested in is on the threshold of the intensity of the electric field ![]() for the system to become chaotic. To do this, we use the Poincaré stroboscopic map [19] , Lyapunov parameter [19] , distance between two nearby trajectories, and the Fourier transformation to see the the power spectrum [19] . If Lyapunov exponent of the trajectory is positive, if the distance between two nearby trajectories grows, and if the Fourier transformation of the trajectory has a continuous component, one can be sure that the trajectory is chaotic.
for the system to become chaotic. To do this, we use the Poincaré stroboscopic map [19] , Lyapunov parameter [19] , distance between two nearby trajectories, and the Fourier transformation to see the the power spectrum [19] . If Lyapunov exponent of the trajectory is positive, if the distance between two nearby trajectories grows, and if the Fourier transformation of the trajectory has a continuous component, one can be sure that the trajectory is chaotic.
5. Numerical Results
Let us consider the diatomic molecule BeO and the initial conditions near the weak critical point![]() , with
, with ![]() between
between ![]() to
to![]() , and with
, and with![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() , and
, and![]() . Taking 10 different initial conditions
. Taking 10 different initial conditions ![]() on the men-
on the men-
tioned range of values near ![]() point, we make the analysis of each trajectory with the tool mentioned on the last section as a function of the magnitude of the electric field
point, we make the analysis of each trajectory with the tool mentioned on the last section as a function of the magnitude of the electric field![]() . For electric fields such that
. For electric fields such that ![]() the trajectories are quasi-periodic, the trajectories on the phase space
the trajectories are quasi-periodic, the trajectories on the phase space ![]() are closed ellipses-like curves, the Lyapunov is not positive, trajectories which are initially infinitesimally separated remain infinitesimally sepa- rated, and the Fourier transformation show only peaks (as it was mentioned before where the regular motion was shown on the phase space). These elements show that the behavior of the system is regular at these magnitude of electric field.
are closed ellipses-like curves, the Lyapunov is not positive, trajectories which are initially infinitesimally separated remain infinitesimally sepa- rated, and the Fourier transformation show only peaks (as it was mentioned before where the regular motion was shown on the phase space). These elements show that the behavior of the system is regular at these magnitude of electric field.
For an intensity of the electric field such that![]() , Figure 3 shows the Lyapunov as a function of time, which becomes positive. Figure 4 shows the Poincaré map (stroboscopic map), which becomes diffused. Figure 5 shows the separation (as a function of time) between two nearby trajectories, with sudden very big va- lues, and Figure 6 shows the discrete Fourier transformation of one of the ten trajectories, showing a continuos
, Figure 3 shows the Lyapunov as a function of time, which becomes positive. Figure 4 shows the Poincaré map (stroboscopic map), which becomes diffused. Figure 5 shows the separation (as a function of time) between two nearby trajectories, with sudden very big va- lues, and Figure 6 shows the discrete Fourier transformation of one of the ten trajectories, showing a continuos
![]()
Figure 5. Distance between two trajectories.
![]()
Figure 6. Discrete Fourier transformation of![]() .
.
component. As we can see clearly from these figures, this trajectory is chaotic and the system behaves as chaotic system (the same was done for the other nine trajectories).
When initial conditions ![]() are chosen outside the range
are chosen outside the range ![]() and with
and with![]() , or close to the critical point with
, or close to the critical point with![]() , the behavior of the trajectories is regular at this intensity of the electric field. The transition region (just for
, the behavior of the trajectories is regular at this intensity of the electric field. The transition region (just for![]() ) is not presented in this study. This analysis was done for each molecule listed on Appendix A, finding the threshold for the system to become chaotic with initial conditions close to its associated
) is not presented in this study. This analysis was done for each molecule listed on Appendix A, finding the threshold for the system to become chaotic with initial conditions close to its associated ![]() critical value. For the above initial conditions and for several higher values of the electric field, we checked the chaotic behavior of the the trajectories.
critical value. For the above initial conditions and for several higher values of the electric field, we checked the chaotic behavior of the the trajectories.
Now, choosing the initial conditions close to the critical value![]() , the behavior of the diatomic molecule is regular for intensities of the electric field such that
, the behavior of the diatomic molecule is regular for intensities of the electric field such that![]() . Ten trajectories were chosen with
. Ten trajectories were chosen with ![]() in the range
in the range![]() . The phase space has ellipse like figure, the Lyapunov ex- ponent is non positive, two trajectories, initially infinitesimally separated, remain infinitesimally separated, and the Fourier transformation presents just peaks. This mean that up to this amplitude of electric field, the tra- jectories with these initial conditions presents a regular behavior (figures are not shown for these statements, but Figure 2 before can be taken as a reference of this regular behavior).
. The phase space has ellipse like figure, the Lyapunov ex- ponent is non positive, two trajectories, initially infinitesimally separated, remain infinitesimally separated, and the Fourier transformation presents just peaks. This mean that up to this amplitude of electric field, the tra- jectories with these initial conditions presents a regular behavior (figures are not shown for these statements, but Figure 2 before can be taken as a reference of this regular behavior).
For an intensity field such that![]() , Figure 7 shows the Lyapunov exponent as a function of time, Figure 8 shows the distance between two nearby trajectories as a function of time, Figure 9 shows the stroboscopic map, and Figure 10 shows the discrete Fourier transformation of one of the trajectories.
, Figure 7 shows the Lyapunov exponent as a function of time, Figure 8 shows the distance between two nearby trajectories as a function of time, Figure 9 shows the stroboscopic map, and Figure 10 shows the discrete Fourier transformation of one of the trajectories.
![]()
Figure 7. Lyapunov’s exponent as a function of time.
![]()
Figure 8. Distance between two trajectories.
![]()
Figure 10. Discrete Fourier transformation of a![]() .
.
These figures show that the trajectories are chaotic with this aptitude of electric field. In fact we checked that the same happen independently of the initial conditions chosen and for higher values of the magnitude of electric field. The transition region (just for![]() ) is not presented in this study. The same analysis was done for each molecule listed on Appendix A to find its threshold electric field for appearing the chaotic behavior. The table on Appendix B shows the threshold values of the electric field for the appearing of chaotic behavior of the trajectories around the weak critical point
) is not presented in this study. The same analysis was done for each molecule listed on Appendix A to find its threshold electric field for appearing the chaotic behavior. The table on Appendix B shows the threshold values of the electric field for the appearing of chaotic behavior of the trajectories around the weak critical point ![]() and the strong critical point
and the strong critical point![]() . Of
. Of
course, if a trajectory is chaotic around the critical point![]() , it will be chaotic with respect the cri-
, it will be chaotic with respect the cri-
tical point![]() .
.
6. Conclusion and Comments
We presented the study of the classical chaotic behavior of a diatomic molecule driven by a circularly polarized resonant electric field. The double resonance system appears from expanding up to fourth order of approximation the Morse’s potential and angular momentum. Chaotic behavior of trajectories around the weak critical point appears at much weaker electric field strength than the strength of the electric field needed to appear the chaotic behavior of trajectories around the strong critical points. This result points out the possible chaotic behavior of double nonlinear resonant systems depending on its initial condition. The exact transition region to chaotic behavior will be presented in other articles. The gap (weak-strong) on the thresholds of the electric field strength to occur the chaotic behavior may be important for the study of diatomic molecules in different environments and for quantum dynamical studies.
Appendix A
Appendix B