Implementation of Chaotic Analysis on River Discharge Time Series ()
1. Introduction
Changing patterns of river flow have potentially significant impacts on water quality, water abstraction, flooding and habitat availability for a range of aquatic and riparian species. It is suggested that water resource planning may need to account for these changes before many of them become statistically significant [1] . For a good understanding on the basins characteristics, the gauged data must have a good analysis. During the past few decades, hydrologists are in a comprehensive query for an appropriate type of analysis for hydrological data. Influenced by the fast-advancing researches on chaotic analysis in the physics, many researchers have been inspired by the new developments in chaos theory. The theory of chaos showed its applicability in solving a wide class of problems in many areas of natural sciences. A chaotic system is defined as a deterministic system, in which small changes in the initial conditions may lead to completely different behavior in the future [2] . Despite being driven by deterministic dynamics, signal from the chaotic system is often indistinguishable from a random process. The discovery of the reality that very simple deterministic systems can produce irregular time series, have dragged researchers into the era of chaos theory. However, chaotic signal analysis is still a novel approach in many areas related to civil engineering [3] . Although the literature of chaotic analysis in hydrology is still limited and can be considered as infancy, there are some good and efficient studies which can prove the evidence of chaotic behavior in daily discharge data e.g. [4] -[13] . Even the primary objective of those studies were on investigating the existence of chaos in hydrological processes, other aspects such as prediction e.g. [6] [8] [9] [14] [15] , noise level determination and noise reduction e.g. [8] [16] were also given due consideration. Differing views have also been reported on the applicability of chaos theory and related methods to hydrological problems. As a brief review of different approaches; the view expressed by Pasternack [17] is based on questioning whether hydrological systems are deterministic or stochastic. His research was focused on using the correlation dimension method (CDM) and comparing it with the performance of stochastic surrogates such as an autoregressive moving average (ARMA) model. His contention was that the CDM had significant problems in its application. However, Liaw et al. [18] commented that the embedding parameters, mainly the delay time, for phase-space reconstruction had not been properly selected. In view of this, they further argued that the attractor reconstructed via the correlation integral analysis as well as surrogate data analysis could not actually represent the dynamic behavior of the underlying system dynamics. Another view by Koutsoyiannis [19] was based on shedding light from a theoretical ground for the application of low dimensional chaos theory to hydrological time series and uses both synthetic and typical gauged data to support his views. Islam & Sivakumar [20] , Lisi & Villi [21] , Liu et al. [9] , Ghorbani et al. [22] , suggested the possibility of accurate stream flow predictions using nonlinear deterministic approaches. Elshorbagy et al. [23] performed noise reduction and missing data estimation, Qingfang and Yuhua [24] developed a new local linear prediction model for chaotic stream flow series. Moreover, there are also debates between these views and the published literature on the hydrological applications as reported above [16] .
This paper consists of implementation of three nonlinear dynamic methods on daily river discharge data. The first one is the phase space analysis, which describes the evolution of the behavior of a nonlinear system and reconstruction using the delay-time method of embedding theorem that was suggested by Takens [25] . The delay time for the reconstruction was chosen after examining the first minimum of the output of average mutual information (AMI) method. Embedding dimension of the phase space was estimated using the false nearest neighbor algorithm (FNN). In terms of the dimensionality analysis, the correlation dimension method (CDM) was applied where the method provides identification of chaotic behavior in terms of dimensionality. Time Series Analysis package program (TISEAN version 3.0.1) [26] was used to calculate the CDM. In the last part of the case study, the local prediction model (LPM) was applied to predict daily discharge time series. The results of study are quite satisfactory to identify Yesil Irmak River as exhibiting chaotic characteristics.
2. Methodology
2.1. Phase Space Reconstruction
The nature of dynamics of a real-world system may be stochastic, deterministic or in between. The character of a system can be identified, at least as a preliminary indicator, by using the phase space concept. A popular method for identification of phase space of a time series was presented by Takens [25] . The theory of deterministic chaos enabled the development of new methods for analyzing the observed time series. In a new approach, time series is assumed to be generated by a nonlinear dynamic system with d degrees of freedom. Therefore to have a better view, it is necessary to construct an appropriate series of state vectors 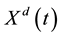 with delay coordinates in the d-dimensional phase space as Equation (1):
with delay coordinates in the d-dimensional phase space as Equation (1):
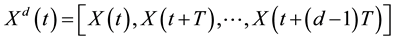 (1)
(1)
where, T is the delay time and, d is the term referring to the embedding dimension. The driven systems whose dynamics can be reduced to a set of inherently deterministic behaviors, their trajectories converge towards the subset of the phase space, called the attractor.
2.1.1. Average Mutual Information
The time delay  can be defined by means of average mutual information (AMI) method [27] . AMI defines how the measurements
can be defined by means of average mutual information (AMI) method [27] . AMI defines how the measurements  at time t, is connected in an information theoretic fashion to measurements
at time t, is connected in an information theoretic fashion to measurements 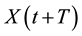 at time
at time  [28] . The average mutual information is defined in Equation (2):
[28] . The average mutual information is defined in Equation (2):
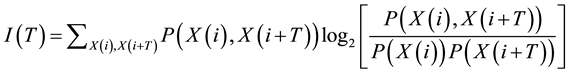 (2)
(2)
where, i is total number of samples. 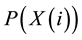 and
and 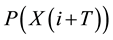 are individual probabilities for the measurements of
are individual probabilities for the measurements of  and
and .
.  are the joint probability density for measurements
are the joint probability density for measurements 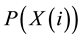 and
and . The appropriate time delay ( ) is defined as the first minimum of the average mutual information
. The appropriate time delay ( ) is defined as the first minimum of the average mutual information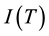 , where the values of
, where the values of 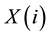 and
and ![]() are enough independent of each other to be useful as coordinates in a time delay vector. But they are not completely independent as to have no connection with each other at all [28] .
are enough independent of each other to be useful as coordinates in a time delay vector. But they are not completely independent as to have no connection with each other at all [28] .
2.1.2. False Nearest Neighbor Algorithm
The false nearest neighbor (FNN) algorithm [29] provides information on the optimal embedding dimension of the phase space (in other words, number of dominant variables) for representing the system dynamics. It examines, in dimension m, the nearest neighbor ![]() of every vector Yj, as it behaves in dimension
of every vector Yj, as it behaves in dimension![]() . If the vector
. If the vector ![]() is a true neighbor of Yj, it comes to the neighborhood of Yj through dynamical origins. On the other hand, if the vector
is a true neighbor of Yj, it comes to the neighborhood of Yj through dynamical origins. On the other hand, if the vector ![]() moves far away from vector Yj by increasing the dimension, m, it is declared as a false nearest neigh boras it arrives in the neighborhood of Yj of the dimension m by projection from a distant part of the attractor. When the percentage of these false nearest neighbors drops to zero, the geometric structure of the attractor has been unfolded and the orbits of the system are now distinct and do not cross (or overlap). A key step in the false nearest neighbor algorithm is to determine how to decide upon increasing the embedding dimension that a nearest neighbor is false. Two criteria are generally used (Sangoyomi et al., 1996). These are:
moves far away from vector Yj by increasing the dimension, m, it is declared as a false nearest neigh boras it arrives in the neighborhood of Yj of the dimension m by projection from a distant part of the attractor. When the percentage of these false nearest neighbors drops to zero, the geometric structure of the attractor has been unfolded and the orbits of the system are now distinct and do not cross (or overlap). A key step in the false nearest neighbor algorithm is to determine how to decide upon increasing the embedding dimension that a nearest neighbor is false. Two criteria are generally used (Sangoyomi et al., 1996). These are:
1) If![]() , the jth vector has a FNN (where
, the jth vector has a FNN (where ![]() is the distance to the nearest neighbor of the jth vector (i.e.,
is the distance to the nearest neighbor of the jth vector (i.e.,![]() ) in an embedding of dimension
) in an embedding of dimension![]() , and RA is the standard deviation of the time series Xt,
, and RA is the standard deviation of the time series Xt,![]() ).
).
2) If![]() , the jth vector has a FNN (where
, the jth vector has a FNN (where ![]() is a threshold factor (generally between 10 and 50), and the distance
is a threshold factor (generally between 10 and 50), and the distance ![]() is computed to the same neighbor that was identified with embedding m, but with the
is computed to the same neighbor that was identified with embedding m, but with the ![]() coordinate (i.e.,
coordinate (i.e.,![]() ) appended to the jth vector and to its nearest neighbor with embedding [15] . In this study, the false nearest neighbor method was implemented using the TISEAN package [26] and uses the second method above.
) appended to the jth vector and to its nearest neighbor with embedding [15] . In this study, the false nearest neighbor method was implemented using the TISEAN package [26] and uses the second method above.
2.2. System Dimensionality
The estimate of the dimension of the system exhibits the presence of chaos through the structure of the dimension. In this study, the Correlation Dimension Method (CDM) was examined, where the correlation dimension of the system provides signification either the chaotic behavior by the dimension or the embedding dimension. If the system has a fractal dimension, the character of the system is assumed to be chaotic.
2.3. Correlation Dimension Method
CDM is one of the most efficient methods to determine the presence of chaos. The method uses a fractal dimension, which is non-integer for chaotic systems. For an m-dimensional phase space the correlation function ![]() is given by Theiler [30] as in Equation (3):
is given by Theiler [30] as in Equation (3):
![]() (3)
(3)
where H is the Heaviside step function by the Equations (4)-(6):
![]() (4)
(4)
![]() (5)
(5)
and
![]() (6)
(6)
N is the number of points on the reconstructed attractor, r is the radius of the sphere centered on Yi or Yj. If the time series is characterized by an attractor, then for positive values of r the correlation function ![]() is related to the radius r by the following relation, Equation (7):
is related to the radius r by the following relation, Equation (7):
![]() (7)
(7)
where a is a constant; and D2 is the correlation exponent or the slope of the ![]() versus
versus ![]() plot given by Equation (8):
plot given by Equation (8):
![]() (8)
(8)
For a finite dataset, there is a radius r below which there are no pairs of points, when the radius approaches the diameter of the cloud of points, the number of pairs will increase no further as the radius increases (saturation). The scaling region would be found somewhere between depopulation and saturation. When ![]() versus
versus ![]() is plotted for a given embedding dimensions m, the range of
is plotted for a given embedding dimensions m, the range of ![]() where the slope of the curve is approximately constant is called the scaling region. In the scaling region, fractal geometry is indicated. In this region
where the slope of the curve is approximately constant is called the scaling region. In the scaling region, fractal geometry is indicated. In this region ![]() increase as a power of r with the scaling exponent, which indicates the correlation dimension D. If the scaling region vanishes as m increases, then finite value of correlation dimension cannot be obtained, and the system under investigation is considered as stochastic. Local slopes of
increase as a power of r with the scaling exponent, which indicates the correlation dimension D. If the scaling region vanishes as m increases, then finite value of correlation dimension cannot be obtained, and the system under investigation is considered as stochastic. Local slopes of ![]() versus
versus ![]() plot can show scaling region clearly when it exists. Because the local slopes of
plot can show scaling region clearly when it exists. Because the local slopes of ![]() versus
versus ![]() plot often fluctuate dramatically, to identify the scaling region more clearly, we can use Takens-Theiler estimator or smooth Gaussian kernel estimator to estimate correlation dimension [26] . For stochastic process, D2 varies linearly with increasing m, without reaching a saturation value, whereas for deterministic process the value of D2 saturates after a certain m.
plot often fluctuate dramatically, to identify the scaling region more clearly, we can use Takens-Theiler estimator or smooth Gaussian kernel estimator to estimate correlation dimension [26] . For stochastic process, D2 varies linearly with increasing m, without reaching a saturation value, whereas for deterministic process the value of D2 saturates after a certain m.
2.4. Prediction
Local Prediction Method
A correct phase-space reconstruction in a dimension m facilities an interpretation of the underlying dynamics in the form of a m-dimensional map fT. According to Equation (9):
![]() (9)
(9)
where Yj and ![]() are vectors of dimension m, describing the state of the system at times j and
are vectors of dimension m, describing the state of the system at times j and ![]() where they are current and future state respectively. Local approximation entails the subdivision of the fT. domain into many subsets (neighborhoods), in order to determine a proper value for fT. In other words, the dynamics of the system is described step by step locally in the phase space. Before applying reconstruction procedure it is necessary to have some information such as, embedding dimension and delay time. One of the independent coordinates mentioned above is taken as the time series itself. The remaining coordinates are formed by its
where they are current and future state respectively. Local approximation entails the subdivision of the fT. domain into many subsets (neighborhoods), in order to determine a proper value for fT. In other words, the dynamics of the system is described step by step locally in the phase space. Before applying reconstruction procedure it is necessary to have some information such as, embedding dimension and delay time. One of the independent coordinates mentioned above is taken as the time series itself. The remaining coordinates are formed by its ![]() lagged time series shifted by
lagged time series shifted by ![]() multiples of the correlation time T, at which correlation between coordinates become zero. It is assumed that the time series data are generated from a chaotic dynamical system in the
multiples of the correlation time T, at which correlation between coordinates become zero. It is assumed that the time series data are generated from a chaotic dynamical system in the ![]() -dimensional space (
-dimensional space (![]() is the dimension of attractor). In this m-dimensional space, estimating the change of Xi with time performs prediction. Considering the relation between the points Xt and
is the dimension of attractor). In this m-dimensional space, estimating the change of Xi with time performs prediction. Considering the relation between the points Xt and ![]() at time T later on the attractor is approximated by function F as in Equation (10);
at time T later on the attractor is approximated by function F as in Equation (10);
![]() (10)
(10)
In this prediction method, the change of Xt with time on the attractor is assumed to be the same as those of nearby points,![]() . Herein,
. Herein, ![]() is determined by the dth order polynomial
is determined by the dth order polynomial ![]() in Equations (11)-(16):
in Equations (11)-(16):
![]() (11)
(11)
![]() (12)
(12)
where:
![]() (13)
(13)
![]() (14)
(14)
and
![]() (15)
(15)
![]() (16)
(16)
In order to obtain a stable solution, the number of rows in the Jacobian matrix A must satisfy the relation in Equation (17):
![]() (17)
(17)
As stated by Porporato and Ridolfi [8] , even though in the case F are first degree polynomials, the prediction is nonlinear, because during the prediction procedure every point ![]() belongs to a different neighborhood and is therefore defined by different expressions for f [1] .
belongs to a different neighborhood and is therefore defined by different expressions for f [1] .
2.5. Evaluation Criteria
2.5.1. Root Mean Square Error
The Root Mean Square Error (RMSE) is a frequently used measure of the difference between values predicted by a model and the values actually observed from the environment that is being modeled. These individual differences are also called residuals, and the RMSE serves to aggregate them into a single measure of predictive power. The RMSE of a model prediction with respect to the estimated variable Xmodel is defined as the square root of the mean squared error.
![]() (18)
(18)
As shown in Equation (18), Xobs is observed values and Xmodel is modelled values at time/place i. The root- mean-square error (RMSE) statistics calculate the variance of the residual. The RMSE is always positive; the best value is zero; the higher the value, the poor the model performance.
1) Normalized Root Mean Square Error
Non-dimensional forms of the RMSE are useful because often one wants to compare RMSE with different units. Normalize the RMSE to the range of the observed data Equation (19):
![]() (19)
(19)
2.5.2. Correlation Coefficient
The quantity![]() , called the linear correlation coefficient, measures the strength and the direction of a linear relationship between two variables (Equation (20)). The value of R2 takes the value between the
, called the linear correlation coefficient, measures the strength and the direction of a linear relationship between two variables (Equation (20)). The value of R2 takes the value between the ![]() and correlation greater than 0.8 is generally described as strong, whereas a correlation less than 0.5 is generally described as weak.
and correlation greater than 0.8 is generally described as strong, whereas a correlation less than 0.5 is generally described as weak.
![]() (20)
(20)
3. Study Area and Data
The daily discharge data of 4 gauge stations of Turkish General Directorate of State Hydraulic Works (DSİ), on Yesil Irmak River basins were examined. The data contains daily period without any missing data in the dataset. The squared stations on Figure 1 are located in different parts of the basins. Yesil Irmak River is one of the significant water resources of Turkey, especially in terms of hydropower potential daily discharge data over a period of 26 years were used. The data length and the statistical information of each station can be seen in Table 1.
4. Analysis and Results
The entire of the dataset is divided into two parts: the first 25 years (1977-2001) of the data are used in the phase-space reconstruction and identification of system behavior and the subsequent 1 year dataset (2001-2002) is used for prediction.
4.1. Phase Space Reconstruction
The first step to reconstruct the original phase space is estimating the phase parameters which are; the delay time and embedding dimension. The method of average mutual information (AMI) (Equation (2)) was used to quantify the delay time. TISEAN version 3.0.1 package program [28] [31] was used to calculate the FNN to quantify the embedding dimension. The results for each station are summarized in Table 2. A simple visual reconstruction of phase space is possible by plotting Xt versus ![]() as the first step towards showing the presence of an attractor for deterministic chaos in a given time series. The three dimensional graph (for
as the first step towards showing the presence of an attractor for deterministic chaos in a given time series. The three dimensional graph (for![]() ,
, ![]() ,
,![]() ) of the attractors for a sampled station on the basins can be seen in Figure 2.
) of the attractors for a sampled station on the basins can be seen in Figure 2.
![]()
Figure 1. Turkey’s basins of Turkish general directorate of state hydraulic works, the Yesil Irmak river basin.
![]()
Table 1. Statistical values of gauge stations.
4.2. Phase Space Reconstruction Parameters
The CDM is used to calculate the embedding dimension for the dataset, using the delay times in Table 2. Different m values from 1 to 15 are tested to obtain the proper embedding dimension. In Figure 3, it can be seen that the correlation value increases with the embedding dimension up to a certain value and then saturates beyond that value. The saturation of the correlation exponent beyond a certain embedding dimension value is an
![]()
Figure 2. Reconstructed phase space plot by obtained time lag from AMI.
![]()
Figure 3. Relation between correlation dimension and embedding dimension.
![]()
Table 2. Phase space reconstruction parameters.
indication of the existence of deterministic dynamics. The saturated correlation dimensions are shown in Table 3 for each station. Both the finite value of correlation dimension curve and the fractal dimension of the reconstructed trajectory, suggest the possible presence of chaotic behavior in the daily discharge time series.
4.3. Dimension Estimate
The CDM is used to calculate the embedding dimension for the dataset, using the delay times in Table 2. Different m values from 1 to 15 are tested to obtain the proper embedding dimension. In Figure 3, it can be seen that the correlation value increases with the embedding dimension up to a certain value and then saturates beyond that value. The saturation of the correlation exponent beyond a certain embedding dimension value is an indication of the existence of deterministic dynamics. The saturated correlation dimensions are shown in Table 3 for each station. Both the finite value of correlation dimension curve and the fractal dimension of the reconstructed trajectory, suggest the possible presence of chaotic behavior in the daily discharge time series.
4.4. Prediction
Local Prediction
The entire dataset of 26 years was divided into two parts; the first 25 years of data were used in the phase space reconstruction and predictions are made for the subsequent 1 year (2001-2002) of data. Table 4 shows values NRMSE for different embedding dimensions in prediction. The selected evaluation criteria (correlation coefficient (R2) reveal that the best prediction achievement when the optimum embedding dimension (mopt) for the lowest NRMSE is selected. The bold values in Table 4 are the mopt for each station. Figure 4 presents a comparison of the actual daily discharge values and the predicted ones due to the chosen optimum-embedding dimension. The scatter plots of observed and predicted values for each station were used to calculate the selected evaluation criteria R2 to determine the prediction achievement. Such results certainly indicate the appropriateness of the phase-space-based nonlinear prediction technique, employed herein on daily discharge data of the gauge stations of Yesil Irmak River Basin. The selected evaluation criteria (correlation coefficient (R2)) reveal
![]()
Table 3. Correlation dimension of the attractors.
![]()
Table 4. NRMSE for each gauge stations.
that the best prediction achievement when the optimum embedding dimension (mopt) for the lowest NRMSE is selected. The bold values in Table 4 show the mopt for each station. Figure 4 presents a comparison of the actual daily discharge values and the predicted onesdue to the chosen optimum embedding dimension. Figure 4 shows the scatter plots of observed and predicted values for each station. Such results certainly indicate the appropriateness of the phase-space-based nonlinear prediction technique, employed herein on daily discharge data of the gauge stations of Yesil Irmak River Basin.
5. Discussion
This paper investigates possible chaotic behaviors in the daily discharge data from the gauge stations on Yesil Irmak Basin, Turkey. The analysis was performed on 4-gauged stations with a record interval of 26 years (1976- 2002). The focus of the paper was on identifying chaotic behavior in time series with an immediate concern that if there were chaotic dynamics in the series, how they would be carried in practical implementations.
The results in this paper can be summarized as follows:
1) Phase space of the data series was reconstructed. For this purpose, two components (time lag, embedding dimension) were determined. In the case of determining time lag, both average mutual information (AMI) and autocorrelation function are used in literature. Considering the fact that, AMI is the nonlinear form of autocorrelation function, AMI method was used to determine nonlinear correlation time series to determine the time lag for the phase space reconstruction.
2) In phase of determining the embedding dimension, which also determines the degrees of freedom, false nearest neighbors (FNN) [29] was used. The outcome of FNN depends on the delay, the metric and the threshold for determining a neighbor is false or true. The FNN method is the most common method used to determine the embedding dimension; FNN was used to obtain the embedding dimension. Nevertheless, the point of FNN algorithm is very sensitive algorithm to noise [30] [32] should be taken into account.
3) The local prediction model was also applied to evaluate its predictability performance. In this prediction model, the dynamics of the system are described step by step locally in the phase space. The predicted values are in good agreement with the observations by having high values of correlation coefficient.
6. Conclusions
Studies reporting the possible presence of nonlinear determinism in river flow and other hydrologic series have often been criticized, essentially due to the implementation of chaotic analysis method as a nonlinear determinism identification tool. Hence the literature of implementation of nonlinear methods in hydrological processes is still being considered as infancy. An important attempt was made in this study, which addressed this issue by identifying the nonlinear deterministic nature of river flows. Understanding how land and water management practices singly and in combination change stream and river flows is a key to maintaining and restoring natural flow regimes [33] . Overall, this special issue exemplifies the need for multidisciplinary approaches, which are essential for producing reliable assessments, and predictions on the relevance of global change on water resources and quality, which can later be translated into policy issues and implemented by water resource managers at basin scale [34] .
In view of the question of whether a given river flow (or any other hydrologic and geomorphic) series can be modeled better by stochastic methods or by nonlinear deterministic methods has come under increasing scrutiny in recent times [3] . The past two decades of chaos theory in geophysics and hydrology have brought us to a situation that is not only crucial but also critical, and even unique. On one hand, the achievements of the past studies, in particular the promising predictions push us forward to continue research on the application of ideas of chaos theory to hydrological data in our efforts towards improving our understanding and pointing out the issues of the methods as discussed in Section 5. The results obtained by the methods, daily discharge data seems to exhibit nonlinear determinism. Accurate predictions on their evolutions have been achieved using nonlinear deterministic methods. The results either in this study or past researches, present only further indication of the usefulness and appropriateness of the nonlinear deterministic and chaotic concepts in hydrology. Whether such concepts and methods could indeed provide accurate representation of the nonlinear interactions and relationships between the components of a river system indeed remains to be seen [35] .
For this purpose, we strongly believe that it is time for researchers to evaluate the whole basin data (where data are available), to understand the river basin system behavior for an accurate management and control.