Variable Separation and Exact Solutions for the Kadomtsev-Petviashvili Equation ()
1. Introduction
The Kadomtsev-Petviashvili (KP) equation [1] is
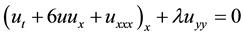 (1)
(1)
where 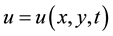 is a real-valued function of two spatial variable x and y, one time variable t, and a constant scalar
is a real-valued function of two spatial variable x and y, one time variable t, and a constant scalar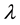 . When
. When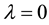 , Equation (1) reduces to the KdV equation. When
, Equation (1) reduces to the KdV equation. When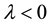 , the equation is known as the KP-I equation which is a good model when surface tension is strong and dominates in very shallow water. When
, the equation is known as the KP-I equation which is a good model when surface tension is strong and dominates in very shallow water. When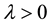 , the equation is called the KP-II equation which is a good model when surface tension is weak or absent.
, the equation is called the KP-II equation which is a good model when surface tension is weak or absent.
This means that the two KP equations have different physical structures and different properties [2] .
It is well known that searching for exact solutions of nonlinear evolution equation arising in mathematical physics plays an important role in nonlinear science fields, since they can provide much physical information and more insight into the physical aspects of the problem and thus lead to further applications [3] . Many powerful methods to seek exact solutions were proposed, for example, the tanh-coth method, the Exp-function method, the Jacobian function method, the Hirotas bilinear form method, the two-soliton method, extended three-wave method, the homoclinic test technique, and so on. But for global smooth solution and local blow up solution, there are quite a few results. Only few of paper studied this type of solution for Landau-Lifishitz equation and Ginzburg-Landau equation and a few equations [4] [5] .
This paper will study global smooth solution and local blow up solution of the KP equation by means of the method of variable separation [6] -[10] , and these solutions conduce to qualitative or numerical analysis for the KP equation.
2. Global Smooth Solutions for the KP Equation
We consider the KP-I equation
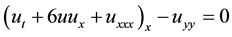 (2)
(2)
Setting 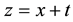 in Equation (2) gives
in Equation (2) gives
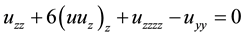 (3)
(3)
Now we suppose the additive separable solution of Equation (3) as
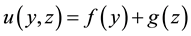 (4)
(4)
where 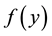 and
and 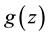 are smooth functions to be determined later.
are smooth functions to be determined later.
Substituting Equation (4) into Equation (3), we discover that
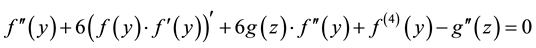 (5)
(5)
by simple transposition, we get
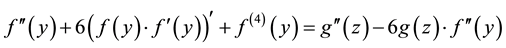 (6)
(6)
In order to obtain nontrivial solution of separation of variables, we demand that 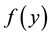 and
and 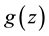 are not all constant. The left side of Equation (6) only depends on variable y, and this has nothing to do with variable z. The right side of Equation (6) is two order linear ordinary differential equation about variable z, and the coefficient is a function of variable y. If the single variable function
are not all constant. The left side of Equation (6) only depends on variable y, and this has nothing to do with variable z. The right side of Equation (6) is two order linear ordinary differential equation about variable z, and the coefficient is a function of variable y. If the single variable function ![]() and
and ![]() satisfy the Equation (6),
satisfy the Equation (6), ![]() and
and ![]() must be constant. Next, we will discuss the existence of nontrivial solution under different conditions.
must be constant. Next, we will discuss the existence of nontrivial solution under different conditions.
Case 1:
![]()
In this case, Equation (6) is reduced to
![]() (7)
(7)
by solving Equation (7), We can be easy to get
![]() (8)
(8)
So, the global smooth solution of Equation (2) is
![]() . (9)
. (9)
where C1, C2 and C3 are arbitrary constants.
Case 2:
![]()
In this case, Equation (6) is transformed into
![]() (10)
(10)
The left side of the Equation (10) is the function about variable z, and the right side is a function about variable y, so ![]() must be constant. Supposing
must be constant. Supposing![]() , we obtain
, we obtain
![]() (11)
(11)
where C1, C2 and C3 are undetermined constants.
Substituting Equation (11) into![]() , we get
, we get
![]() (12)
(12)
In the meantime, Equation (10) is transformed into two order homogeneous linear differential equation with constant coefficients as follows
![]() (13)
(13)
by solving Equation (13), We obtain
![]() (14)
(14)
where C4 and C5 are arbitrary constants.
So, in this case, the global smooth solution of Equation (2) is
![]() (15)
(15)
where C4 and C5 are arbitrary constants.
Case 3:
![]()
In this case, It is assumed that![]() , where
, where ![]() is a constant. So, Equation (6) is transformed into
is a constant. So, Equation (6) is transformed into
![]() (16)
(16)
by assumption, we get
![]() (17)
(17)
where C1, C2 and C3 are undetermined constants.
Substituting Equation (17) into![]() , the following algebraic equations are got.
, the following algebraic equations are got.
![]() (18)
(18)
We obtain two group of solutions by solving Equation (18) as follows
1)![]() ;
;
2)![]() ;
;
Accordingly, the equation ![]() in Equation (16) is transformed into
in Equation (16) is transformed into
![]() (19)
(19)
![]() (20)
(20)
Solving Equation (19), we have![]() , where C4 and C5 are arbitrary constants.
, where C4 and C5 are arbitrary constants.
Solving Equation (20), we have![]() .
.
So, we obtain two group of global smooth solutions of Equation (2) as follows:
![]() (21)
(21)
where C3, C4 and C5 are arbitrary constants, and![]() .
.
![]() (22)
(22)
Case 4:
![]()
In this case, Equation (6) is transformed into
![]() (23)
(23)
Solving![]() , we get
, we get
![]() (24)
(24)
where C1, and C2 are undetermined constants.
Substituting Equation (24) into the equation ![]() in Equation (23), we get
in Equation (23), we get ![]() and
and![]() .
.
Solving the equation ![]() in Equation (23), we obtain
in Equation (23), we obtain
![]() (25)
(25)
where C3 and C4 are arbitrary constants.
So, we obtain the global smooth solutions of Equation (2) as follows:
![]() (26)
(26)
where C2, C3 and C4 are arbitrary constants, and![]() .
.
3. Local Blow up Solutions for the KP Equation
We look for separable solution of the multiplicative form of Equation (3)
![]() (27)
(27)
where ![]() and
and ![]() are smooth functions to be determined later.
are smooth functions to be determined later.
Plugging the form (27) into the nonlinear diffusion Equation (3), we obtain
![]() (28)
(28)
Then ![]() and
and ![]() should satisfy the following nonlinear ordinary differential equations
should satisfy the following nonlinear ordinary differential equations
![]() (29)
(29)
![]() (30)
(30)
where ![]() denotes the separation constant. Solving ordinary differential Equation (29), we get the following explicit special solutions
denotes the separation constant. Solving ordinary differential Equation (29), we get the following explicit special solutions
![]() (31)
(31)
Solving Equation (30), we will discuss both cases as follows:
Case 1:
when![]() , the Equation (30) will be transformed into
, the Equation (30) will be transformed into
![]() (32)
(32)
![]() (33)
(33)
Substituting Equation (31) into Equation (32), we have![]() , for
, for![]() .
.
Solving Equation (33), the solution ![]() is obtained, where C3 is a arbitrary constant.
is obtained, where C3 is a arbitrary constant.
So, in this case, the Equation (2) possesses local blow up solution as follows
![]() (34)
(34)
where C1 and C3 are arbitrary constants with![]() .
.
Case 2:
when![]() , the Equation (30) will be transformed into
, the Equation (30) will be transformed into
![]() (35)
(35)
![]() (36)
(36)
Substituting Equation (31) into Equation (35), we have![]() , where C1 is a arbitrary constant.
, where C1 is a arbitrary constant.
Solving Equation (36), the solution ![]() is obtained, where C5 and C6 are arbitrary constants.
is obtained, where C5 and C6 are arbitrary constants.
In this case, we can not get the blow up solution of Equation (2).
4. Conclusion
It is well known that the method of variable separation is one of the most universal and efficient means for studying linear partial differential equations. Several methods of variable separation for nonlinear partial differential have been suggested until recently. This paper applies the method of variable separation to obtain global smooth solutions and local blow up solutions of the KP equation. These solutions can be used to qualitative or numerical analysis for properties of the KP equation. In the future, we will try to seek for the generalized variable separation solutions by the form of solution ![]() and
and ![]() .
.