Mathematical Models to Simultaneously Determine Overtime Requirements and Schedule Cells ()
1. Introduction
In manufacturing systems, capacity allocation and machine scheduling play an essential role. Typically, capacity requirements are determined first and then detailed scheduling is performed to fit into the determined capacity. The capacity planning establishes the number of machines/workers needed in a process layout environment, number of production lines or cells needed in a cellular environment, number of shifts to be utilized, whether overtime will be done or not, etc. Various approaches have been developed for capacity planning purposes such as capacity bills, resources profiles, rate-based capacity planning, and mathematical modeling, etc. On the other hand, scheduling deals with the detailed allocation of resources established in the capacity planning step to various jobs over a period of time. Scheduling establishes start and completion times of jobs on resources, i.e. machines, cells, production lines and workers.
In a company, each on-time delivered product brings revenue and customer satisfaction; both are essential to maintain the profitability of any company over a long term period. Making a job tardy is highly undesirable for any company. Establishing capacity requirements is a difficult task and it gets even harder when capacity requirements vary from one period to the next. In this situation, using overtime is a feasible method and many companies use that. Therefore, overtime can be used to adjust the capacity to handle the jobs which otherwise become tardy and may lead to poor reputation or in worst case loosing up of valuable customers. Overtimes are of two types: weekend overtime and weekday overtime. This distinction is important in that their costs usually vary. Weekend overtimes are usually more expensive than the weekday overtime because of the change in hourly workforce rate. Therefore, each overtime decision comes with a cost associated with it. This all makes the problem difficult to solve and lead to a NP-hard optimization problem where the weekend and weekday overtime decisions as well as cell loading and job sequencing are performed to maximize the overall net profit. We need to mention that if overtime is needed week after week, this may be an indicator that organization needs to re-assess capacity requirements and adjust regular capacity levels, i.e., increase number of cells, number of machines, etc.
2. Problem Definition
The problem studied in this paper was inspired from an actual textile company. In every planning period (week) there are n jobs to complete using m number of identical cells. Manufacturing cells are popular in the manufacturing world. Cellular Manufacturing (CM) aims to obtain the flexibility to produce a high or moderate variety of low or moderate demand products with high productivity. CM is a type of manufacturing system that consists of manufacturing cell(s) with dissimilar machines needed to produce part family/families. Generally, the products grouped together form a product family. The benefits of CM are lower setup times, smaller lot sizes, lower work-in-process inventory and less space, reduced material handling, and shorter flow time, simpler work flow (Suresh & Kay, 1998 [1] ). Cellular Manufacturing also simplifies planning and control of various tasks floating on the shop floor. Cells are ideally equipped with all of the machines needed to produce a productor product family (independent) and usually follow uni-directional flow (flowshop).
Many textile companies also use cells to enjoy the benefits the cells have to offer. Machines used in cells in textile industry are usually limited to different types of sewing machines such as overlock machines, stitch machines, automatic flat lock sewing machines. In this study, each cell can perform eight operations. The operations performed are briefly discussed in this paragraph. The first operation is cutting and the next three operations require sewing machines. The operations that follow are finishing, ironing, cleaning and packing. Operations 2 and 4 each were performed on two identical machines as they were the slowest operations. It is easy to re-configure cells in the textile industry once products with different requirements are produced as machines and work benches are easier to move around.
In this paper, it is assumed that each job has its own individual due date. The modeling gets complicated in that we need to decide additional capacity requirements at the same time we make scheduling decisions. Any job that cannot be completed by its due date becomes tardy and is assumed lost sales. Having tardy jobs is not desirable as this adversely affects relationships with customers and thus reputation of the firm in the long term. As a result, we allow overtime to minimize the number of tardy jobs. Overtime decisions are made for shifts on a daily basis. Overtime can be done during the weekends (Saturday and Sunday) as well as weekdays. Weekend overtime is done prior to upcoming week. It is also assumed that weekend overtime cost is higher than weekday overtime cost. The overall objective is to maximize profits. Tardy jobs are avoided as long as profit to be made is higher than the corresponding production/overtime costs. There are limitations on weekday and weekend overtime capacities. In this paper, the number of shifts considered is 2. Models can easily be modified to accommodate 1 shift. However, if the company wants to adopt a 3-shift policy, then weekday overtime option has to be eliminated and overtime can only be done during weekends. Lot splitting is not allowed in this study.
We propose mathematical models based on the current overtime workforce handling practices followed by the industries to solve this problem and then compare their performance in this study.
3. Literature Review
Several researchers focused on cell loading problem. Among them, Süer, Saiz, Dagli & Gonzalez [2] andSuer, Saiz & Gonzalez [3] developed several simple cell loading rules for connected and independent cells, respectively. They have tested the performance of these rules against four different performance measures, namely number of tardy jobs, maximum tardiness, total tardiness and utilization. Süer, Vazquez & Cortes [4] developed a hybrid approach of Genetic Algorithms (GA) and local optimizer to minimize number of tardy jobs in a multi-cell environment. In the same study, they have used three different GA approaches; basic GA approach, hybrid GA with local optimizers and finally GA with learning feature. Hybrid GA outperformed basic GA, however, GA with learning improved solutions only marginally. Süer, Arikan & Babayiğit [5] [6] studied cell loading subject to manpower restrictions and developed fuzzy mathematical models to minimize number of tardy jobs and total manpower levels. They have used various fuzzy operators and identified fuzzy operators that can find non-dominated solutions. In their work, number of cells and crew size for each cell were identified in addition to product sequencing decisions.
There are a number of works reported where both cell loading and product sequencing tasks are carried out. Süer & Dagli [7] and Süer, Cosner & Patten [8] discussed models to minimize makespan, machine requirements and manpower transfers. These works first assigned products to cells to minimize makespan and then re-se- quenced the products to minimize manpower requirements. Yarimoglu [9] developed a mathematical model and a genetic algorithm to minimize manpower shortages in cells with synchronized material flow. Synchronized material flow allowed material transfers between stages at regular intervals (e.g., 4 hour in his case).
Some other researchers studied the sequencing of families in a single cell or machine. Nakamura, Yoshida & Hitomi [10] considered sequence-independent group setup in his work and his objective was to minimize total tardiness. Hitomi & Ham [11] also considered sequence-independent setup times for a single machine scheduling problem. Ham, Hitomi, Nakamura & Yoshida [12] developed a branch-and-bound algorithm for the optimal group and job sequence to minimize total flow time keeping the number of tardy jobs minimum. Pan and Wu [13] focused on single machine scheduling problem to minimize mean flow time of all jobs subject to due date satisfaction. They categorized the jobs into groups without family splitting. Gupta and Chantaravarapan [14] studied the single machine scheduling problem to minimize total tardiness considering group technology. Individual due dates and independent family setup times have been used in their problem with no family splitting. Süer and Mese [15] studied the same problem but allowed family splitting as it would be beneficial in many cases.
A number of researchers focused on shoe manufacturing industry and reported various results. These works heavily focused on scheduling jobs on the Rotary Injection Molding Machines. Süer. Santos and Vazquez [16] have developed a three-phase Heuristic Procedure to minimize makespan. Süer, Subramanian and Huang [17] included some heuristic procedures and mathematical models for cell loading and scheduling problem. The objective was to minimize makespan and unlimited availability of the molds was assumed. Later, Huang, Suer and Urs [18] introduced the limited mold availability into the problem for the same objective.
The most important feature of the scheduling problem studied in this paper is that both overtime decisions and detailed scheduling tasks including cell loading and product sequencing are performed simultaneously. Even though there were previous works that considered capacity and scheduling decisions simultaneously before (see Süer, Arikan & Babayiğit [5] [6] ), there is only one work that considers both overtime and scheduling decisions simultaneously (see Mathur and Süer [19] ) in the literature to the best knowledge of the authors. We propose new mathematical models that can be used under varying conditions. The objective is to maximize the profit and it is closely related to finishing jobs on time.
4. Integer Programming Formulation
Maxwell [20] developed a mathematical model to minimize number of tardy jobs on a single machine schedule. Later, Süer, Pico and Santiago [21] extended this model for parallel machine scheduling. In a later study, Süer, Arikan and Babayiğit [5] [6] adapted this model to cell loading problem where jobs are assigned to cells and manpower levels for each cell are identified simultaneously. Süer, Mathur and Ji [19] extended these models where due date equations are modified to allow for overtime decisions. In the models proposed in this paper, the due dates of jobs are modified in a similar way to meet different working conditions. This modification allows us to consider overtime decisions along with cell loading and scheduling. The main logic behind this formulation is that the due time for a job is extended (increased) by the total overtime hours planned before this job is due.
Assume that a job is due Wednesday noon. Assuming only one shift work, then the due time for this job is calculated as 20 hours (8 hours available on Monday, 8 hours available on Tuesday and 4 hours available on Wednesday). Assume that mathematical model proposes to do overtime both on Monday and Tuesday, 3 hours each day. Then the due time of this job becomes 26 hours (=20 + 3 + 3). The proposed mathematical models accommodate this possibility in the formulation. The objective is to maximize profit. All of the jobs should be ordered by the Earliest Due Date (EDD) before model is run (d[1] ≤ d[2] ≤ d[3] ≤ … ≤ d[n]). Similarly p[i] is the processing time of the job in the ith order. It is also assumed that weekend overtime work is done prior to planning week.
In this section, four different integer programming formulations are introduced. Each one of them is based on the observation on overtime workforce handling practices followed by the industries. Indices and parameters used throughout the paper are listed below.
Indices:
i: job index
j: cell index
t: day index
q: shift index
Parameters:
n: number of jobs
m: number of identical cells
pi: processing time of job i (in hours)
di: due time of job i (in hours)
shift[i]v: shift in which ith job is due
si: sales price of job i
cwd: weekday overtime cost per shift
cwe: weekend overtime cost per shift
dayi: due day of job i depending on due time
otwd: length of weekday overtime (3 hours)
otwe: length of weekend overtime (8 hours)
4.1. Mathematical Model 1
The unique feature about this model is that it allows different weekday and weekend overtime decisions with respect to different cells and also workers are paid for the complete period of overtime slot even if they finish the work early in the overtime period. The model is capable of determining the schedule of jobs on each cell as well as handling the capacity of each cell by making overtime decisions.
The objective is to maximize the net profit as shown in Equation (1). This is computed by subtracting all weekend and weekday overtime costs from the sales revenue of the products finished by their due time. Weekday overtime can be done on any of the five working days and weekend overtime can be done on Saturday and/or Sunday. The first set of constraints (Equation (2)) enforce that early jobs are completed before their due times (original or extended). The second set of constraints (Equation (3)) guarantees that a job can assigned to at most one cell. The values of decision variables xij and ottjq will be known once the mathematical model is solved.
Decision Variables:
xij: 1 if job i is assigned to cell j, 0 otherwise
ottjq: 1 if there is overtime on day t in shift q of cell j, 0 otherwise
Objective Function:
 (1)
(1)
Subject to:
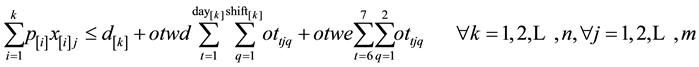 (2)
(2)
 (3)
(3)
4.2. Mathematical Model 2
Model 2 is similar to Model 1 in that it allows different weekday and weekend overtime work with respect to different cells. However, the difference between two models comes from the practice that overtime workforces can be hired and paid for the fraction of the overtime slot in this Model. In this model, overtime decision variable is modified as given below.
ottjq: fraction of overtime to do on day t in shift q of cell j between 0 and 1
4.3. Mathematical Model 3
The model has been first proposed by Süer, Mathur and Ji [19] . The unique feature about this model is that a uniform overtime strategy is applied, i.e., all of the cells get to do the same overtime whenever an overtime decision is made. This may be important in some companies where all the workers are given the same opportunity to do overtime and gain additional income. Overtime workforces are hired and paid for the complete period of overtime slot on all cells. In this case, overtime decision variable is simplified as shown below.
ottq: 1 if there is overtime on day t in shift q, 0 otherwise
The objective is to maximize the net profit as shown in Equation (4). The first set of constraints (Equation (5)) enforce that early jobs are completed before their due times (original or extended). The second set of constraints (Equation (6)) guarantees that a job can assigned to at most one cell.
Objective Function:
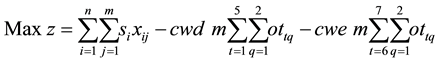 (4)
(4)
Subject to:
 (5)
(5)
 (6)
(6)
4.4. Mathematical Model 4
Model 4 is similar to Model 3 in that all of the cells get to do the same overtime whenever an overtime decision is made. However, the difference between two models is that overtime workforces can be hired and paid for the fraction of the overtime slot in Model 4. In this case, overtime decision variable is modified as shown below.
ottq: fraction of overtime to do on day t in shift q between 0 and 1
The main features of four mathematical models are summarized in Table 1.
5. A Numerical Illustration
An example case is illustrated in this section. A 20-job and 2-cell problem is solved by all four mathematical models using ILOG OPL 6.3 optimization tool. In each mathematical model illustration, three tables and one figure are given. The first table shows the sequence of jobs assigned to each cell; the second table shows the corresponding overtime decisions for the problem; the third table shows the original due day, due shift and due time; revenue generated from each job, processing times, detailed computations of completion times and revised due dates (Di*) based on overtime decisions; and the Gantt chart is given in the corresponding figure. It is important to note that the weekend overtime starts before the week starts. For example, to complete a job before the set due date (say on Monday evening), overtime can be performed on Saturday and/or Sunday shifts.
5.1. Solution by Mathematical Model 1
This model assigned 18 out of 20 jobs to cells. Jobs 8 and 14 are not assigned to any cell (hence tardy and in this paper lost customer orders). The jobs assigned to each cell are summarized in Table 2. Table 3 shows when and on what cell we need to do overtime during the week. Table 4 shows the details of all computations. When a job is tardy, its completion time is not listed since it is assumed as lost sales (for example for job 8 in Table 4). Job 1 in Table 4 is due Monday, shift 1, and original due time is 5.79 hours and it has been assigned to cell 1. Since we allow overtime on Sunday shift 1 for eight hours on cell 1, the due date is taken as (D1*=) 13.79 hours (=5.79 + 8). Similar adjustment are made for all jobs, i.e. jobs original due dates are modified (increased) by considering the overtimes scheduled before their due date. On cell 1, Monday shift1 is of regular eight hours whereas on cell 2, Monday shift 1 is of 11 hours (including overtime). On both the cells, Monday shift 2 are 11 hours (including overtimes); Tuesday shift 1 and shift 2 are 11 (including overtimes) and eight hours respectively; and the remaining weekdays are all regular eight hours. Whereas on the weekends, only cell 1 needs eight hours of overtime only on Sunday shift1 as shown in Table 3 and Figure 1.
![]()
Table 1. Characteristics of Mathematical models over Overtime decision variables.
![]()
Table 2. Sequence of jobs assigned to each cell for model 1.
![]()
Table 3. Overtime decisions for model 1.
![]()
Figure 1. Gantt chart for model 1 solution.
![]()
Table 4. Detailed computations for model 1 solution.
5.2. Solution by Mathematical Model 2
This model also assigned 18 out of 20 jobs to cells as shown in Table 5. On both cells, Monday shifts are 11 hours (including overtimes); Tuesday shift1 and shift 2 are 11 (including overtimes) and 8 hours, respectively; and the remaining weekdays except for Friday shift 1 are all regular eight hours. On cell 1, Friday shift 1 is of 8.39 hours (=8 + 0.13*3) whereas on cell 2 it is of 8.02 hours (=8 + 0.0067*3) including overtimes. On the weekends, overtimes are required on Sunday shift 1 of 3 hours (=0.375*8) on cell 1 and on Saturday shift 1 of 1.12 hours (=0.14*8) on cell 2 as shown in Table 6. In this case, the due date for job 1 (D1*=) is computed as 11.79 hours since we allow partial overtime on Sunday shift 1 for three hours (=0.375*8) and also allow three hour overtime on shift1 on Monday on cell 1 (=5.79 + 3 + 3). Table 7 shows the details of all computations and the corresponding Gantt chart is given in Figure 2.
5.3. Solution by Mathematical Model 3
This model resulted in three tardy jobs. The sequence of jobs assigned to cells is given in Table 8. Overtime decisions are summarized in Table 9. On both the cells, Monday as well as Tuesday shift 1 and shift 2 are of 11 hours (including overtimes) and eight hours respectively; and the remaining days are all regular eight hours. On the other hand, no overtime work is scheduled for weekends. In this model, the due date for job 1 (D1*=) is taken as 8.79 hours (=5.79 + 3) as we allow three-hour overtime on Monday shift 1 on both cells. The detailed computations are summarized in Table 10 and the corresponding Gantt chart is given in Figure 3.
![]()
Table 5. Sequence of jobs assigned to each cell for model 2.
![]()
Table 6. Overtime decisions for model 2.
![]()
Table 7. Detailed computations for model 2 solution.
![]()
Table 8. Sequence of jobs assigned to each cell for model 3.
![]()
Table 9. Overtime decisions for model 3.
![]()
Table 10. Detailed computations for model 3 solution.
![]()
Figure 2. Gantt chart for model 2 solution.
![]()
Figure 3. Gantt chart for model 3 solution.
5.4. Solution by Mathematical Model 4
This model also led to 18 jobs being completed before their due dates. The sequence of jobs assigned to cells is given in Table 11. Overtime decisions are summarized in Table 12. In Table 13, for example Job 1, is due Monday, shift 1, and original due time is 5.79 hours. Since we allow partial overtime of 2.21 hours (=0.27625*8) on Saturday shift1 and also allow three hour overtime on Monday shift 1 on both the cells, the due date is taken as (D1*=) 11 hours (=5.79 + 2.21 + 3). Similar adjustment are made for all jobs, i.e. jobs original due dates are modified (increased) by considering the overtimes scheduled before their due date. On both the cells, Monday shift 1 and shift 2 are 11 hours (including overtimes) each; Tuesday shift 1 and shift 2 are 11 hours (including overtimes) and regular of eight hours, respectively; Thursday shift 1 and shift 2 are regular eight hours and 8.09 hours (=8 + 0.03*3) (including overtime) respectively and the remaining days are all regular eight hours. Whereas on the weekend on both the cells, overtime is required only on Saturday shift 1 of 2.21 hours (=0.27625*8) as shown in Figure 4.
6. Experimentation Results
In this section, experimentation results are discussed. Eight problems were formed with 20, 30, 40, 50, 60, 70, 80 and 90 jobs; and 2, 2, 2, 2, 2, 4, 4 and 5 cells, respectively (problems 1, 2, 3, 4, 5, 6, 7 and 8 respectively). The data generated is inspired from the Textile Company where the problem was observed. Each product undergoes eight different operations. The upper and lower range of processing times for each operation were identified based on the sample data provided by the company. The processing times were generated randomly from this interval for the corresponding operation in each data set. Processing times for operations 1, 2, 3, 4, 5, 6, 7 and 8 follow uniform distributions UD(2, 4), US(1, 2.5), UD(1, 3.5), UD(1, 2), UD(1, 2), UD(1, 2), UD(1, 2), and UD(0.2, 2), respectively. The batch size of each product follows uniform distribution UD(50, 250). The production rate for each product is identified based on the bottleneck machine. The processing time (hr) for a job is computed dividing its batch size with its production rate. The due time of each job is generated by using Equation (7). Products’ due days (considering one week as a period) as well as a due shifts (1 or 2) are calculated on the basis of due time. The sale price of each job is assigned by using Equation (8). The hourly labor rates for regular time, weekday overtime and weekend overtime are taken as $10, $15, and $20, respectively. The weekend overtime is limited to 8 hours per shift whereas weekday overtime is restricted to 3 hours per shift.
![]() (7)
(7)
![]() (8)
(8)
6.1. Results of Mathematical Model 1
The results of Mathematical Model1 are shown in Table 14. The results show that mathematical model produced tardy jobs in spite of the fact that overtime was done both during the weekdays and weekend for some problems (problems 1, 4, and 5). In problems 2, 7, 8, weekend overtime was not done even though there was a
![]()
Table 11. Sequence of jobs assigned to each cell for model 4.
![]()
Table 12. Overtime decisions for model 4.
![]()
Table 13. Detailed computations for model 4 solution.
![]()
Figure 4. Gantt chart for model 4 solution.
tardy job in the system. Doing overtime would cost more than profit to be obtained from this tardy in these problems. In problem 3, tardy job(s) were avoided by doing overtime both weekdays and weekends. Finally, in problem 6, weekday overtime was sufficient to avoid tardy jobs. The execution times of models varied from 1 second to almost 57 minutes.
6.2. Results of Mathematical Model 2
The results of Mathematical Model 2 are summarized in Table 15. There were tardy jobs in problems 1, 2, and 5 even though overtime was done both during the weekdays and weekend. In problems 3 and 4, tardy job(s) were avoided by doing overtime both weekdays and weekend. Finally, in problems 6, 7 and 8, weekday overtime was sufficient to avoid tardy jobs. The execution times of models were less than 2 seconds.
6.3. Results of Mathematical Model 3
The results of Mathematical Model 3 are given in Table 16. In problems 4 and 5, there were tardy jobs even though overtime was done both during the weekdays and weekend. In problems 1 and 2, weekend overtime was not done even though there were tardy jobs in the system. Finally, in problems 3, 6 and 8, tardy jobs were avoided by doing overtime either on weekdays or both weekdays and weekend. Problem 7 could not be solved due to memory restrictions. The execution times of models varied from 1 second to almost 2 hours 4 minutes.
6.4. Results of Mathematical Model 4
The results of Mathematical Model 4 are shown in Table 17. The results show that mathematical model produced tardy jobs in spite of the fact that overtime was done both during the weekdays and weekend for some problems (problems 1, 4, and 5). In problems 2, 7, 8, weekend overtime was not done even though there was a tardy job in the system. Doing overtime would cost more than profit to be obtained from this tardy in these problems. In problem 3, tardy job(s) were avoided by doing overtime both weekdays and weekends. Finally, in problem 6, weekday overtime was sufficient to avoid tardy jobs. The execution times of models varied from 1 second to almost 57 minutes.
6.5. Comparison of Mathematical Models
In this section, the results of four mathematical models are compared. The highest profit for each problem was obtained with mathematical model 2 (MM2). MM4 found the second highest profit in six of the problems tested and tied with MM2 in problems 2 and 4. The main reason why MM2 and MM4 obtained better results is due to the fact that overtime decision variables are allowed to take fractional values thus lowering the overtime cost. On the other hand, MM1 got the third highest profit values in five problems and tied with MM3 in the remaining three problems. Based on the results, the preference of models can be listed as 1) MM2; 2) MM4; 3) MM1; and 4) MM3. It is also important to note that the difference between the best and worst profit values in the problems tested here is less than 0.80% in seven out of eight problems and it is 1.62% in the remaining problem. The results of four mathematical models are summarized in Table 18.
![]()
Table 18. Performance comparison between mathematical models.
7. Conclusions and Future Work
In this study, various mathematical models are proposed to determine overtime requirements, assign jobs to cells and also determine the sequence of jobs simultaneously in each cell. The objective is to maximize the profit to be obtained from the completion of products on time. These mathematical models represent different overtime workforce handling practices followed by industries. The problem has been inspired from a textile company. Data used in the experimentation has been generated based on the collected sample real data from the same company.
The result of a mathematical model gives us a weekly complete schedule with the overtime decisions on each weekend and weekday on each shift and on each cell. Moreover, it tells us the load on cells and also the schedule of jobs on each cell. The selection of an appropriate mathematical model obviously depends on practices of different companies. However, if there is a chance to select among these models, then Mathematical Model 2 would be the best choice as it outperforms all other mathematical models in all of the problems tested. Mathematical Model 2 allows partial overtime periods. It also allows different overtime periods on different cells. This flexibility in the problem formulation led to the best results. Mathematical model 4 tied the results in two of the problems and got the second best results in the rest of the problems. Indeed, the gap between the best and worst results when all models were considered was smaller than 1.62%.
The experimentation also showed that mathematical models could solve large problems relatively fast. Especially Mathematical Model 2 took less than nine seconds to find the optimal solution in all of the problems tested. This may be another factor that would make Mathematical Model 2 a desirable one in addition to the fact that it found the highest profits among all models. We could solve problems up to 90 jobs per period. The number of jobs mentioned in the textile company had to handle on a weekly basis roughly varied 20 - 40 jobs. As a result, these models can be used to make these decisions in similar industrial settings.
Some of the future work planned includes addition of setup times to the models. Allowing lot splitting is another option. We may also consider a minimum limit on overtime in the future models. Another possible extension is to allow tardy jobs but apply penalty (tardiness cost) when that occurs. In this study we assumed that cells were identical. It is also possible to consider cell size alternatives. One last note about the topic is that if a company uses overtime regularly, it may be worthwhile to adjust capacity levels (increase) to avoid additional overtime costs.