1. Introduction
Tolerance analysis is the branch of mechanical design dedicated to studying the impact of the manufacturing tolerances on the functional constraints of any mechanical system. Minkowski sums of polytopes are useful to model the cumulative stack-up of the pieces and thus, to check whether the final assembly respects such constraints or not, see [2] [3]. We are aware of the algorithms presented in [4]-[7] but we believe that neither the list of all edges nor facets are mandatory to perform the operation. So we only rely on the set of vertices to describe both polytope operands. In a first part we deal with a “natural way’’ to solve this problem based on the use of the convex hulls. Then we introduce an algorithm able to take advantage of the properties of the sums of polytopes to speed-up the process. We finally conclude with optimization hints and a geometric interpretation.
2. Basic Properties
2.1. Minkowski Sums
Given two sets 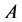 and
and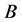 , let
, let 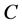 be the Minkowski sum of
be the Minkowski sum of  and
and 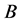
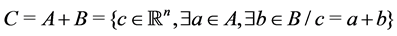
2.2. Polytopes
A polytope is defined as the convex hull of a finite set of points, called the 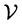 -representation, or as the bounded intersection of a finite set of half-spaces, called the
-representation, or as the bounded intersection of a finite set of half-spaces, called the 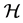 -representation. The Minkowski-Weyl theorem states that both definitions are equivalent.
-representation. The Minkowski-Weyl theorem states that both definitions are equivalent.
3. Sum of V-Polytopes
In this paper we deal with 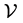 -polytopes i.e. defined as the convex hull of a finite number of points. We note
-polytopes i.e. defined as the convex hull of a finite number of points. We note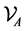 ,
, 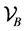 and
and  the list of vertices of the polytopes
the list of vertices of the polytopes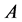 ,
, 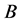 and
and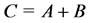 . We call
. We call 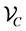 the list of Minkowski vertices. We note
the list of Minkowski vertices. We note 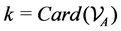 and
and![]() .
.
3.1. Uniqueness of the Minkowski Vertices Decomposition
Let ![]() and
and ![]() be two
be two ![]() -polytopes and
-polytopes and![]() ,
, ![]() their respective lists of vertices. Let
their respective lists of vertices. Let ![]() and
and ![]() where
where ![]() and
and![]() .
.
![]() (1)
(1)
We recall that in [4], we see that the vertex ![]() of
of![]() , as a face, can be written as the Minkowski sum of a face from
, as a face, can be written as the Minkowski sum of a face from ![]() and a face from
and a face from![]() . For obvious reasons of dimension,
. For obvious reasons of dimension, ![]() is necessarily the sum of a vertex of
is necessarily the sum of a vertex of ![]() and a vertex of
and a vertex of![]() . Moreover, in the same article, Fukuda shows that its decomposition is unique.
. Moreover, in the same article, Fukuda shows that its decomposition is unique.
Reciprocally let ![]() and
and ![]() be vertices from polytopes
be vertices from polytopes ![]() and
and ![]() such that
such that ![]() is unique. Let
is unique. Let ![]() and
and ![]() such as
such as ![]() with
with ![]() and
and ![]() because the decomposition of
because the decomposition of ![]() in elements from
in elements from ![]() and
and ![]() is unique. Given that
is unique. Given that ![]() and
and ![]() are two vertices, we have
are two vertices, we have ![]() and
and ![]() which implies
which implies![]() . As a consequence
. As a consequence ![]() is a vertex of
is a vertex of![]() .
.
3.2. Summing Two Lists of Vertices
Let ![]() and
and ![]() be two
be two ![]() -polytopes and
-polytopes and![]() ,
, ![]() their lists of vertices, let
their lists of vertices, let![]() .
.
![]() (2)
(2)
We know that ![]() because a Minkowski vertex has to be the sum of vertices from
because a Minkowski vertex has to be the sum of vertices from ![]() and
and ![]() so
so![]() .
.
The reciprocal is obvious as ![]() as
as ![]() is a convex set.
is a convex set.
At this step an algorithm removing all points which are not vertices of ![]() from
from ![]() could be applied to compute
could be applied to compute![]() . The basic idea is the following: if we can build a hyperplane separating
. The basic idea is the following: if we can build a hyperplane separating ![]() from the other points of
from the other points of ![]() then we have a Minkowski vertex, otherwise
then we have a Minkowski vertex, otherwise ![]() is not an extreme point of the polytope
is not an extreme point of the polytope![]() . The process trying to split the cloud of points is illustrated in Figure 1.
. The process trying to split the cloud of points is illustrated in Figure 1.
To perform such a task, a popular technique given in [8] solves the following linear programming system. In the case of summing polytopes, testing whether the point ![]() is a Minkowski vertex or not, means finding
is a Minkowski vertex or not, means finding ![]() from a system of
from a system of ![]() inequalities:
inequalities:
![]()
So if we define the matrix ![]()
then ![]()
![]()
Figure 1. Computing the vertices of the sum of two V-poly- topes through a convex hull algorithm.
The corresponding method is detailed in Algorithm 2. Now we would like to find a way to reduce the size of the main matrix ![]() as it is function of the product
as it is function of the product![]() .
.
![]()
3.3. Constructing the New Algorithm
In this section we want to use the basic property 1 characterizing a Minkowski vertex. Then the algorithm computes, as done before, all sums of pairs ![]() and checks whether there exists a pair
and checks whether there exists a pair ![]() with
with![]() ,
, ![]() such as
such as![]() . If it is the case then
. If it is the case then![]() , otherwise
, otherwise![]() .
.
![]() with
with ![]() and
and ![]()
![]() with
with ![]() and
and![]() .
.
We get the following system:
![]()
That is to say with matrices and under the hypothesis of positivity for both vectors ![]() and
and![]() :
:
![]()
We are not in the case of the linear feasibility problem as there is at least one obvious solution:
![]()
The question is to know whether it is unique or not. This first solution is a vertex ![]() of a polyhedron in
of a polyhedron in ![]() that verifies
that verifies ![]() equality constraints with positive coefficients. The algorithm tries to build another solution making use of linear programming techniques. We can note that the polyhedron is in fact a polytope because it is bounded. The reason is that, by hypothesis, the set in
equality constraints with positive coefficients. The algorithm tries to build another solution making use of linear programming techniques. We can note that the polyhedron is in fact a polytope because it is bounded. The reason is that, by hypothesis, the set in ![]() of convex combinations of the vertices
of convex combinations of the vertices ![]() is bounded as it defines the polytope
is bounded as it defines the polytope![]() . Same thing for
. Same thing for ![]() in
in![]() . So in
. So in ![]() the set of points verifying both constraints simultaneously is bounded too.
the set of points verifying both constraints simultaneously is bounded too.
So we can write it in a more general form:
![]()
where only the second member is function of ![]() and
and![]() .
.
It gives the linear programming system:
![]() (3)
(3)
Thanks to this system we have now the basic property the algorithm relies on:
![]() (4)
(4)
![]() there exists only one pair
there exists only one pair ![]() to reach the maximum
to reach the maximum ![]() as
as ![]() and
and ![]()
![]() the decomposition of
the decomposition of ![]() is unique
is unique ![]()
It is also interesting to note that when the maximum ![]() has been reached:
has been reached: ![]()
![]()
3.4. Optimizing the New Algorithm and Geometric Interpretation
The current state of the art runs ![]() linear programming algorithms and thus is solvable in polynomial time. We presented the data such that the matrix
linear programming algorithms and thus is solvable in polynomial time. We presented the data such that the matrix ![]() is invariant and the parametrization is stored in both the second member and the objective function, so one can take advantage of this structure to save computation time. A straight idea could be using the classical sensitivity analysis techniques to test whether
is invariant and the parametrization is stored in both the second member and the objective function, so one can take advantage of this structure to save computation time. A straight idea could be using the classical sensitivity analysis techniques to test whether ![]() is a Minkowski vertex or not from the previous steps, instead of restarting the computations from scratch at each iteration.
is a Minkowski vertex or not from the previous steps, instead of restarting the computations from scratch at each iteration.
Let’s switch now to the geometric interpretation, given![]() , let’s consider the cone generated by all the edges attached to
, let’s consider the cone generated by all the edges attached to ![]() and pointing towards its neighbour vertices. After translating its apex to the origin
and pointing towards its neighbour vertices. After translating its apex to the origin![]() , we call this cone
, we call this cone ![]() and we call
and we call ![]() the cone created by the same technique with the vertex
the cone created by the same technique with the vertex ![]() in the polytope
in the polytope![]() .
.
The method tries to build a pair, if it exists, ![]() with
with![]() ,
, ![]() such that
such that![]() . Let’s introduce the variable
. Let’s introduce the variable![]() , and the straight line
, and the straight line![]() .
.
So the question about ![]() being or not a Minkowski vertex can be presented this way:
being or not a Minkowski vertex can be presented this way:
![]() (5)
(5)
The existence of a straight line inside the reunion of the cones is equivalent to the existence of a pair ![]() such that
such that ![]() which is equivalent to the fact that
which is equivalent to the fact that ![]() is not a Minkowski vertex. This is illustrated in Figure 2. The property becomes obvious when we understand that if
is not a Minkowski vertex. This is illustrated in Figure 2. The property becomes obvious when we understand that if ![]() exists in
exists in ![]() then
then ![]() and
and ![]() are symmetric with respect to the origin. Once a straight line has been found inside the reunion of two cones, we can test this inclusion with the same straight line for another pair of cones, here is the geometric interpretation of an improved version of the algorithm making use of what has been computed in the previous steps.
are symmetric with respect to the origin. Once a straight line has been found inside the reunion of two cones, we can test this inclusion with the same straight line for another pair of cones, here is the geometric interpretation of an improved version of the algorithm making use of what has been computed in the previous steps.
We can resume the property writing it as an intersection introducing the cone ![]() being the symmetric of
being the symmetric of ![]() with respect to the origin.
with respect to the origin.
![]() (6)
(6)
4. Conclusion
In this paper, our algorithm goes beyond the scope of simply finding the vertices of a cloud of points. That’s why we have characterized the Minkowski vertices. However, among all the properties, some of them are not easily exploitable in an algorithm. In all the cases we have worked directly in the polytopes ![]() and
and![]() , i.e. in the primal spaces and only with the polytopes
, i.e. in the primal spaces and only with the polytopes ![]() -descriptions. Other approaches use dual objects such as normal fans and dual cones. References can be found in [6] [7] [9] but they need more than the
-descriptions. Other approaches use dual objects such as normal fans and dual cones. References can be found in [6] [7] [9] but they need more than the ![]() -description for the polytopes they handle. This can be problematic as obtaining the double description can turn out to be impossible in high dimensions, see [4] where Fukuda uses both vertices and edges. Reference [6] works in
-description for the polytopes they handle. This can be problematic as obtaining the double description can turn out to be impossible in high dimensions, see [4] where Fukuda uses both vertices and edges. Reference [6] works in ![]() in a dual space where it intersects dual cones attached to the vertices, and it can be considered as the dual version
in a dual space where it intersects dual cones attached to the vertices, and it can be considered as the dual version
![]()
Figure 2. ![]() is not a vertex of C = A + B as
is not a vertex of C = A + B as![]() .
.
of property 6 where the intersection is computed with primal cones. It actually implements Weibel’s approach described in [9]. Such a method has been recently extended to any dimension for ![]() -polytopes in [7].
-polytopes in [7].
Special Thanks
We would like to thank Pr Pierre Calka from the LMRS in Rouen University for his precious help in writing this article.