Robust Sliding Mode Control for Nonlinear Discrete-Time Delayed Systems Based on Neural Network ()
1. Introduction
Time delay is undesirable parameter which is often encountered in various engineering systems, such as mechanical systems, chemical systems, and so on. The time delay degrades the system performance and leads to instability of the system. As a design tool for robust motion control system, SMC has been well designed for a wide range of nonlinear systems in both continuous time and discrete time. SMC is robust to parametric uncertainties and insensitive to unknown disturbance. SMC has been studied in seventies by the name of variable structure control (VSC) [1] [2] . VSC, is characterized by discontinuous feedback control law which switches the system in a predefined subspace [3] . Its implementation by a digital system requires sampling interval which leads to chattering. Over the past few decades, considerable attention has been reported to the stability analysis of continuous time delay systems by using different approaches [4] - [10] . In [4] , robust controller has been designed for continuous time delay system using Ricacati equation approach. Considerable, attention has been given using LMI approach for stabilization of continuous time delay systems [5] - [8] . An adaptive control approach has been proposed for the control of time delay system [9] [10] . A discrete SMC (DSMC) is important when we implement robust control digitally with slow sampling rate. It is important to note that DSMC cannot be obtained from its continuous counterpart by simple conversion. Since modeling inaccuracy and external conditions lead to uncertainties, disturbances and nonlinearities in systems. Hence, the stability analysis of uncertain discrete-time delay systems have been studied over past few years with different control approaches have been well documented in [11] and reference therein. Moreover, in the above papers, the unknown nonlinearities have not been investigated. In [12] , a robust control of uncertain nonlinear state delayed system, which gives a conservative condition of control, is presented. In recent years, many papers have reported the problem of SMC for state delay uncertain systems [13] - [17] . Most of these papers for uncertain time delay systems involve norm- bound nonlinearities which are treated as external disturbances. Adaptive multilayer neural control schemes for the control of complex nonlinear systems have shown great results over past few years. Now, it is an established fact that unknown nonlinear functions can be approximated from neural network. Neural network appears a powerful tool for nonlinear control problems [18] - [20] . In [21] , the SMC have been used for control of uncertain state-delay system with unknown nonlinearity. In this work, Chebyshev Neural Network is used to estimate the unknown nonlinearity and linear matrix inequalities (LMI) conditions were derived to ensure the asymptotic stability on the defined sliding surface. Adaptive SMC for a class of discrete nonlinear systems was proposed. The proposed controller uses switching function with adaptive term to reduce the problem of chattering. Artificial neural network (ANN) was used for approximation of modeling errors. The nonlinearity is strictly positive and bounded away from zero [22] . In [23] , a new SMC has been used to control the unknown nonlinear discrete-time systems. The chattering is reduced as compared to normal discrete-time sliding mode control using time varying gain.
This paper proposes a discrete-time sliding mode controller for a class of state delay nonlinear discrete systems. The unknown nonlinear functions in system dynamics is approximated using Chebyshev Neural Networks (CNNs). New weight update laws are derived to make this scheme adaptive. The stability of state delay system is taken care by carefully selecting Lyapunov-Krasovskii functional candidate. Thus conservative, sufficient conditions were derived which was represented by an appropriate set of LMIs.
The paper organization is as follows. Section 2 presents the CNN structure. Problem formulation and preliminaries are elaborated in Section 3. Section 4 presents controller design is stated in detail. The stability analysis is presented in Section 5. The effectiveness of proposed scheme is validates through simulation results in Section 6. The note ends with concluding remarks in Section 7.
Notations:  denotes Euclidean norm,
denotes Euclidean norm,  implies Frobenius norm. The
implies Frobenius norm. The 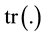 stands for trace of matrix.
stands for trace of matrix.
2. CNN Structure
An ANN is a simple interconnected group of nonlinear elements, which has the capability to represents nonlinear functions. The representation accuracy depends on the ANN complexity, i.e., the number of elements and the way in which they are interconnected [24] .
There is different ANN configuration available, like feed forward network such as multilayer perceptron (MLP), radial basis function (RBF) networks, Chebyshev neural network (CNN) etc. The MLP network has certain disadvantage that it requires a large amount of computation for learning. The RBF network can effectively learn from discontinuities and local variations. The problem with this network is choosing an appropriate set of RBF centers for effective learning. A single-layer functional link artificial neural network (FLANN) in which the need of hidden layer is eliminated by expanding the input pattern using Chebyshev polynomials. The main advantage of this network is that it requires much less computation as compared to a multilayer perceptron (MLP).
CNN is a functional link network (FLN) based on Chebyshev polynomials. CNN architecture has two main parts, namely, numerical transformation and learning [25] . In numerical transformation we use finite set of Chebyshev polynomials as a functional expansion (FE) of input pattern. The learning part is a functional-link neural network based on Chebyshev polynomials. The Chebyshev polynomials can be obtained by a recursive formula
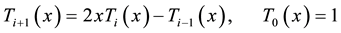 (1)
(1)
where, 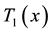 are Chebyshev polynomials,
are Chebyshev polynomials, 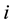 is the order of polynomials chosen and here
is the order of polynomials chosen and here 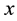 is a scalar quantity. The different choices of
is a scalar quantity. The different choices of 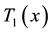 are
are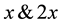 .
.
The output of single layer neural network is given by
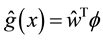 (2)
(2)
where, 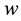 are the weights and
are the weights and 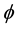 is the suitable basis function of neural network. Based on the approximation property of CNN [27] -[30] , there exist ideal weights
is the suitable basis function of neural network. Based on the approximation property of CNN [27] -[30] , there exist ideal weights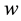 , so that the function
, so that the function 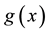 to be approximated can be represented as
to be approximated can be represented as
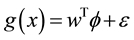 (3)
(3)
where, 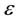 is the CNN functional reconstruction error vector and
is the CNN functional reconstruction error vector and ![]() is bounded.
is bounded.
3. Problem Formulation
Consider the following discrete-time state delay system as in [26] (Figure 1)
![]() (4)
(4)
where, ![]() and
and ![]() denote the state and input vectors respectively.
denote the state and input vectors respectively. ![]() and
and ![]() are real constant matrices with appropriate dimensions.
are real constant matrices with appropriate dimensions. ![]() is a unknown nonlinear function of a given system in Equation (4), and
is a unknown nonlinear function of a given system in Equation (4), and ![]() is a positive number representing delay.
is a positive number representing delay.
For the system given in (4) the sliding mode controller is obtained as
![]() (5)
(5)
where ![]() is the approximated value of the nonlinear function.
is the approximated value of the nonlinear function.
The objective of this work is to guarantee the stability of sliding mode controller in Equation (5) of the nonlinear system Equation (4), so that the system stays on the sliding surface.
4. Controller Design
The first step in the design of discrete-time SMC control algorithm would be the design of sliding surface. The linear sliding surface is defined as:
![]() (6)
(6)
where ![]() is a real matrix of appropriate dimensions.
is a real matrix of appropriate dimensions.
For a system to be asymptotically stable, the sliding surface is defined as follows.
![]() (7)
(7)
The second step is to design a control law which can guarantee the sliding mode reaching condition of the given linear sliding surface. The obtained control law is given in Equation (5) will force the trajectory of the system to move towards the sliding surface monotonically and causes zigzag motion around the sliding surface.
5. Stability Analysis
The following assumptions are needed for the stability analysis of the given unknown nonlinear system [26] .
Assumption 1: The state delay h is a constant time delay that is basically induced by the network transmission. For constant time delay the lower and upper bounds are assumed to be identical.
Assumption 2: The nonlinear function ![]() in the system is unknown and bounded.
in the system is unknown and bounded.
Assumption 3: (Bounded Ideal NN Weights): The ideal NN weights ![]() are bounded so that
are bounded so that![]() , with
, with ![]() a known bound. The symbol
a known bound. The symbol ![]() denotes the Frobenius norm, i.e. given a matrix
denotes the Frobenius norm, i.e. given a matrix![]() , the Frobenius norm is given by,
, the Frobenius norm is given by,
![]()
Assumption 4: Let![]() , where
, where ![]() is a
is a ![]() symmetric matrix, and
symmetric matrix, and ![]() and
and ![]() are the
are the ![]() -column vectors.
-column vectors.
Theorem 1:
Given the system in Equation (4) and Assumptions 1 - 4, sliding mode control law Equation (5), the estimated NN weights are given by
![]() (8)
(8)
with the condition are
![]() (9)
(9)
![]() (10)
(10)
Suppose there exist an ![]() positive-definite matrix
positive-definite matrix![]() , an
, an ![]() nonnegative-definite matrix
nonnegative-definite matrix![]() , an
, an ![]() nonnegative-definite matrix
nonnegative-definite matrix ![]() and
and ![]() symmetric matrix
symmetric matrix ![]() such that following LMI holds,
such that following LMI holds,
![]() (11)
(11)
Thus by properly selecting the control gain and the design parameters, the state trajectory is reaching on the designed sliding surface.
Proof: Choose Lyapunov-Krasovskii functional candidate,
![]() (12)
(12)
where
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
And
![]() (17)
(17)
Substituting Equations (13)-(16) in Equation (12)
![]() (18)
(18)
and
![]() (19)
(19)
where
![]() (20)
(20)
Since![]() ,
, ![]() is a positive-definite and
is a positive-definite and ![]() is a nonnegative-definite,
is a nonnegative-definite, ![]() is then positive-definite. Therefore,
is then positive-definite. Therefore,
![]() (21)
(21)
Substituting Equation (18) and (19) in Equation (21),
![]() (22)
(22)
Substituting Equation (5) in Equation (21) and using Assumption 3 in Equation (22)
![]() (23)
(23)
After some mathematical manipulations in Equation (23),
![]() (24)
(24)
where
![]() (25)
(25)
Collecting the terms together and substitute control law Equation (5) in Equation (24) yields
![]() (26)
(26)
where
![]() (27)
(27)
with tuning law in Equation (8) , Equation (26) will be,
![]() (28)
(28)
substituting Equations (25), (27) in Equation (28)
![]() (29)
(29)
Manipulating the nonquadratic terms using the following inequality ![]() (which turns into equality if and only if
(which turns into equality if and only if ![]() we get,
we get,
![]() (30)
(30)
where
![]() (31)
(31)
![]() (32)
(32)
In Equation (30), ![]() is guaranteed to remain negative as long as
is guaranteed to remain negative as long as
![]()
Since the first two terms in Equation (30) are satisfying the condition in Equation (9), (10), next four terms are satisfying the LMI in Equation (11). Therefore, we conclude that the system in Equation (4) is stable with control law Equation (5) and LMI in Equation (11).
6. Simulation Results
In this section, a numerical example is presented to validate the performance and effectiveness of the nonlinear discrete-time system proposed in Equation (4). Consider the set of parameters for the given system
![]() ,
,
and
![]()
The fixed time delay is assumed to be![]() . The proposed system has initial condition of states
. The proposed system has initial condition of states ![]() and
and ![]() are chosen as
are chosen as![]() . The LMI in H1) are solved by using Matlab LMI Toolbox and the values of
. The LMI in H1) are solved by using Matlab LMI Toolbox and the values of![]() ,
, ![]() ,
, ![]() and
and ![]() are obtained as
are obtained as
![]() ,
,
![]() ,
,
The trajectories of the system states ![]() and
and ![]() are shown in Figure 2 and Figure 3. It is observed in Figure 2 and Figure 3 that the states of the sliding motion approach to zero quickly. Figure 4 demonstrates that the controller robustly stabilizes the system by sliding mode technique with fixed time delay. The simulation results confirm the stability of the system and show the effectiveness of proposed scheme.
are shown in Figure 2 and Figure 3. It is observed in Figure 2 and Figure 3 that the states of the sliding motion approach to zero quickly. Figure 4 demonstrates that the controller robustly stabilizes the system by sliding mode technique with fixed time delay. The simulation results confirm the stability of the system and show the effectiveness of proposed scheme.
7. Conclusion
In this paper, a sliding mode control for a class of unknown nonlinear discrete-time system is proposed ,which results in small chattering motion in both control signal and system output. A Chebyshev Neural Network is used to approximate the unknown system dynamics. A new learning algorithm for neural network approximation is proposed. This neural network based sliding mode control approach guarantees the system state trajectory to the defined sliding surface. An LMI based sufficient condition for the asymptotic stability of the sliding mode dynamics is derived by means of a Lyapunov-Krasovskii approach. Simulation results are validating the effectiveness of proposed scheme.