Relationship between Sea Surface Single Carrier Waves and Decreasing Pressures of Atmosphere Lower Boundary ()
1. Introduction
The existence of rogue waves is now universally recognized [1] - [21] and many images on the extent of damage caused by these monsters of the ocean are available. However, the physics of processes responsible for the formation (or origin) and propagation of these phenomena as well as their prediction is not completely understood. Contrary to developed country researchers’ opinion, physics of spectacular phenomenon like rogue waves is not easily obtainable by the only use of advance data provided by high technology equipment like: Powerful Computers; sophisticated WIS (Weather Information Systems); Wind’s Profilers; Radar Drones; Lidar Drones; Satellites, etc. Indeed, rogue waves are a combination of multi-spectral processes that occur under the thermodynamic and dynamic accuracy conditions. Mathematical models [22] -[25] offer more tremendous opportunities for understanding of the systems whose physics is, at the present level of our knowledge, difficult to obtain. To allow a better understanding of the behavior of rogue waves triggered by tornadoes in terms of their origin and spatio- temporal evolution, that is, their motion and also in terms of mechanical transformations that these systems may suffer in their dealings with other systems, the nonlinear physics of off-balance systems is developed in the specific case of strong agitations constantly seen on the surface of extensive and deep rivers, when they are crossed by an atmosphere’s low pressure system (tornadoes, cyclones, hurricanes, etc.). A mathematical model based on Navier-Stokes and Euler Lagrange equations coupled with assumptions derived from the literature on the nature of the training locations (or birth places) of rogue waves is developed to enhance the physics of processes responsible for the formation (or origin) of the waves associated with atmosphere’s low pressure systems. Indeed, Navier-Stokes and Euler Lagrange equations provide evidence that waves may form on the surface of water as a reaction to impact of the decreasing pressures of the atmosphere lower boundary. It is precisely in this case, the materialization of action triggers reaction Physics’ Principle and then of a manifestation among many others of the evidence of Atmosphere-Oceans coupling. The rogue waves births’ constraints are mainly the need for both consistent water (i.e., extensive-deep rivers) and potential velocity flow domain. Numerical simulations, based on the use of the NLSE (nonlinear Schrödinger equation) on amplitude and phase modulations are performed to validate our mathematical model on the births of rogue waves associated with atmosphere’s low pres- sure systems.
2. Kinematics’ Constraints Associated with Births of Tornadoes’ (or Cyclones’) Rogue Waves
The general fluid continuity equation is given by:
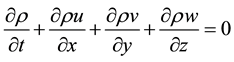 (1)
(1)
This leads to the continuity equation for an incompressible fluid
 (2)
(2)
The kinematic boundary conditions
 (3)
(3)
where 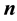 is the unit vector normal to the boundary surfaces and
is the unit vector normal to the boundary surfaces and  is the sea surface elevation. Hence:
is the sea surface elevation. Hence:
 (4)
(4)
Equation of motion in natural coordinates
 (5)
(5)
For an inviscid fluid, Equation (5) is simplify to
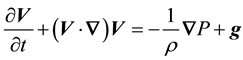 (6)
(6)
When the flow is irrotational, one can write
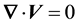 (7)
(7)
The related velocity potential is so given by
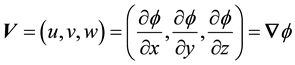 (8)
(8)
The continuity equation in regard to irrotational flow
 (9)
(9)
The kinematic boundary condition at the bottom of irrotational flow
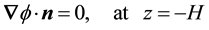 (10)
(10)
The kinematic boundary condition at the surface of the same flow
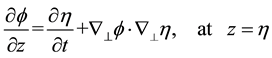 (11)
(11)
Integrating Equation (6) with respect to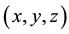 , leads to Bernoulli equation. Arbitrary functions of integration
, leads to Bernoulli equation. Arbitrary functions of integration ,
, 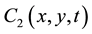 ,
, ![]() must be the same function
must be the same function![]() , which can be absorbed by the velocity
, which can be absorbed by the velocity
potential, yielding exactly the same flow
![]() (12)
(12)
where, ![]() is the density of liquid water;
is the density of liquid water; ![]() the sea-level dynamic pressure and P0 the sea-level static pressure.
the sea-level dynamic pressure and P0 the sea-level static pressure.
Due to the smallest-vertical extend of oceans with regard to earth’s radius, we can consider ![]() constant throughout it
constant throughout it ![]() making the gravitational force conservative and able to derive from a potential energy through- out the ocean. We can also neglect the surface tension.
making the gravitational force conservative and able to derive from a potential energy through- out the ocean. We can also neglect the surface tension.
When atmosphere’s low pressure systems (LOW on Figure 1) cross the ocean: The atmosphere low boundary decreasing pressures field above the ocean replaces ![]() in Equation (12).
in Equation (12).
![]()
Figure 1. LOW (low pressure systems) and HIGH (higher pressure system) on a mean sea-level pressure (millibars) map.
And then, taking ![]() constant and equal to 0 at
constant and equal to 0 at![]() , gives Formula (13) which describes the geometry of ocean’s surface single carrier waves:
, gives Formula (13) which describes the geometry of ocean’s surface single carrier waves:
![]() (13)
(13)
Formula (13) is our mathematical model on the occurrence of oceans’ surface single carrier waves associated with atmosphere’s low pressure systems (i.e., the mainly origin of tornadoes; cyclones or hurricanes related waves).
- ![]() is the sea surface temperature;
is the sea surface temperature;
- ![]() is the sea-level decreasing pressure below atmosphere’s low pressure systems (Figures 2(a)-(d));
is the sea-level decreasing pressure below atmosphere’s low pressure systems (Figures 2(a)-(d));
- ![]() is the sea-level static pressure
is the sea-level static pressure![]() .
.
According to Formula (13), the height of single carrier waves depends mainly on low pressure deepest. i.e.,![]() .
.
3. Implementation of NLSE
According to the nonlinear Schrödinger equation (NLSE), the combination of unstable waves can trigger a sin- gle wave which can reach up to three or five times the amplitude of the single carrier waves (that is, the wave energy is basically concentrated in a single wave number). Let’s consider a surface wave whose main compo-
nent ![]() is of the form
is of the form![]() , then Benjamin-Feir integral equation developed in [3] for this type of wave has the form:
, then Benjamin-Feir integral equation developed in [3] for this type of wave has the form:
![]() (14)
(14)
We consider the case of energy concentrated mainly around two-wave numbers
![]() (15)
(15)
where A and B satisfy the Coupled Nonlinear Schrödinger Equations [22] :
![]() (16)
(16)
![]() (17)
(17)
Here, we took into account that the energy distribution is almost monochromatic and the Taylor expansion of the pulse around the two wave numbers.
If the energy concentrated mainly around a wave number, the evolution of a waveform produced by a group unstable wave only on the nonlinear Schrodinger equation is:
![]() (18)
(18)
Putting the previous relation (18) under the dimensionless form, we obtain the nonlinear Schrödinger equation rewrites in the form [23] [24] :
![]() (19)
(19)
This is an integrable equation. We can find solution which form is:
![]() (20)
(20)
where ![]() and
and ![]() are both arbitrary functions. We assume that
are both arbitrary functions. We assume that ![]() is real function.
is real function.
Substitution of (20) in (19), gives (21):
![]() (21)
(21)
We are interested in a homoclinic orbit to the fixed point and we obtain finally the solution (22):
![]() (22)
(22)
![]() (23)
(23)
Below is an exact analytical solution of Equation (19):
![]() (24)
(24)
with ![]() and
and![]() .
.
Relation (24) can reach to a family of spatiotemporal solutions of breather type with the advantage that they describe the plane wave. The rational solitons’ family can be transform to Peregrine breather type of solution:
![]() (25)
(25)
4. Results and Discussion
According to scientists’ common opinion, questions raised by observations lead to physics’ laws while observations can in no way serve as physics’ laws. Indeed, advance equipment like powerful computer; sophisticated WIS (Weather Information Systems); Wind’s Profilers; Radar Drones; Lidar Drones; Satellites, etc., cannot completely solve problems regarding the adverse effects of climate change without the contributions of performing mathematical models on physics of processes responsible of that climate change. Earth’s ecosystem is considerably modified by adverse effects of climate change and this irreversible process reveals human beans vulnerability vis-à-vis of phenomenon like rogue waves; landslides; coastal cities floods, etc. Geometries of sea surface carrier waves associated with atmosphere low pressure systems are drawn on Figures 3(a)-(c) and Figure 4. Taking into account the Barograph Traces, one can see that the atmosphere low pressure systems can take more than two days to cross a Weather Station. Barograph traces also show that the deepest of impacts on sea- level pressure depends on many weather’s parameters. Figures 3(a)-(c) represent carrier-waves for different wave numbers. Single carrier waves Interferences (or combinations) are shown on Figure 4. The resulting wave (Figure 4) reveals that Interferences are mainly constructive in the case of sea-surface carrier waves. On Figure 5(a) and Figure 5(b), one can see lands’ and oceans’ tornadoes respectively. Overland Tornadoes are daily phe- nomena (Figure 5(a)) which occur only during sunny days due to additional greenhouse effects [26] [27] . The same thermodynamics’ process occurs over oceans even by night (Figure 5(b)) and in this case, it escapes to vi- gilance of weather alert instruments and represents a higher risk for airline pilots as well as seamen’s. This is, according to Mbane’s previous publications [26] -[28] , the main reason why many planes have disappeared when crossing oceans by night. There is convincing evidence that Air France and Malaysian Airlines planes are recent victims of nightly oceans’ tornadoes epiphenomenon.
5. Conclusion
Many avenues of scientific research (including ours) are now open to better understand the physics, structure, composition and functioning of atmosphere lower pressure systems and their impacts on oceans, mainly in the case of rogue waves’ implementation. Indeed, Earth’s atmosphere is in contact with the oceans, oceans affect it, but in return it acts upon them: We speak of oceans-atmosphere coupling. To study the physics of rogue waves associated by tornadoes (cyclones or hurricanes) in terms of their origin, the nonlinear physics of off-balance systems has been developed in the specific case of strong agitations constantly seen on the surface of extensive and deep rivers, when these rivers are crossed by an atmosphere’s low pressure system. Euler-Lagrange and
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figures 3.(a)-(c) Simulations of geometry of ocean surface single carrier waves associated with atmosphere’s low pressure systems for different wave numbers ((a) K0 = 1; (b) K0 = 2 and (c) K0 = 4.0).
![]()
Figure 4. Simulations of geometry of oceans’ surface multispectral carrier wave associated with atmosphere low pressure systems shown on Figure 5(b).
![]()
![]() (a) (b)
(a) (b)
Figure 5. (a)-(b) Tornadoes 3D-profiles ((a), above the land; (b), above the ocean). One may note that: Tornadoes can occur even by night on the Oceans (b) and represent in this case a higher risk for aircrafts. This thermodynamics’ process is impossible by night on the Land (due to land’s thermal inertia).
Navier-Stokes equations have provide evidence that waves may form on the surface of water as a reaction to impacts of sea-level decreasing pressures of the atmosphere lower boundary. That is precisely the materializa- tion of action triggers reaction Physics’ Principle and then of a manifestation among many others of the convinc- ing evidence of Atmosphere-Oceans coupling. A mathematical model based on the Navier-Stokes equations coupled with assumptions derived from advance data bases on rogue waves has been developed to allow a better understanding of processes responsible for the formation (or origin) of sea surface waves. The rogue waves births’ constraints are mainly the need for availability of both consistent water (i.e., extensive-deep rivers) and potential velocity flow. Numerical simulations, based on NLSE (nonlinear Schrödinger equation) on amplitude and phase modulations has been successfully performed to validate our relationship between sea-surface strong agitations and decreasing pressure of atmosphere lower boundary.
NOTES
*Corresponding author.