Infinite Number of Disjoint Chaotic Subsystems of Cellular Automaton Rule 106

Gaocang Zhao¹, Fangyue Chen¹, Weifeng Jin²

¹School of Science, Hangzhou Dianzi University, Hangzhou, China.
²College of Pharmaceutical Sciences, Zhejiang Chinese Medical University, Hangzhou, China.

DOI: 10.4236/am.2014.520303                

Abstract

In this paper, the dynamics of rule 106, a Chua’s hyper Bernoulli cellular automata rule, is studied and discussed from the viewpoint of symbolic dynamics. It is presented that rule 106 defines a chaotic subsystem which is topologically mixing and possesses the positive topologically entropy. An effective method of constructing its chaotic subsystems is proposed. Indeed, it is interesting to find that this rule is filled with infinitely many disjoint chaotic subsystems. Special attention is paid to each subsystem on which rule 106 is topologically mixing and possesses the positive topologically entropy. Therefore, it is natural to argue that the intrinsic complexity of rule 106 is high from this viewpoint.

Keywords

Cellular Automata, Chaos, Topologically Entropy, Topologically Mixing, Subsystem

1. Introduction

Cellular Automata (CA), first conceived around 1950 by von Neumann [1] , are a class of spatially and temporally discrete mathematical structure by local interactions and an inherently parallel form of evolution. The whole structure is able to produce complex and interesting dynamical phenomena by means of designing simple transition rule. Due to their simple mathematical constructions and distinguishing features, CA have drawn a great deal of attention from various scientists. In 1969, the study of topological dynamics of CA was developed by Hedlund [2] , who viewed one-dimensional CA in the context of symbolic dynamics as endo- morphisms of the shift dynamical system, where the main results are the characterizations of surjective and open CA. In 1970, Conway proposed game of life [3] , which received widespread interests among researchers in different fields. In the early 1980s, Wolfram proposed CA as models for physical systems exhibiting complex or even chaos behaviors and elementary CA (ECA) that consist of a one-dimensional array of finite binary cells, each interacting only with the two nearest neighbors [4] - [6] . He classified 256 ECA rules informally into four classes using dynamical concepts like periodicity, stability and chaos. In 2002, Wolfram introduced his work A New Kind of Science [6] . Based on this work, Chua et al. have concluded the dynamics of ECA from a nonlinear dynamics perspective [7] - [10] . And he divided 256 ECA rules into four classes: period- rules, Bernoulli-shift rules, complex Bernoulli-shift rules and hyper Bernoulli-shift rules.

Gratefully, the research of CA has drawn more and more scientists’ attention in the last 20 years. Many concepts of topological dynamics have been used to describe and classify them [11] - [15] . And the dynamical properties of some robust Bernoulli-shift rules have been studied in the bi-infinite symbolic sequence space [14] , [15] . Rule 106 belonging to hyper Bernoulli-shift rules possesses complex and distinctive dynamical behaviors. In a paper [16] , the authors introduced the notion of permutivity of a map in a certain variable. Then they proved that every one-dimensional CA based on the local rule which is permutive either in the leftmost or rightmost variable is Devaney chaotic. Rule 106 is in this situation. Presently, this work is devoted to an in-depth study of rule 106 from the perspective of nonlinear dynamics under the framework of bi-infinite symbolic sequence space, and mainly studies the complex dynamics on its infinite number of subsystems.

The rest of the paper is organized as follows: Section 2 presents the basic concepts of one-dimensional CA and symbolic dynamics. Based on these concepts, it shows a subsystem of rule 106. Section 3 explores the complex dynamical behaviors of rule 106. Section 4 describes that there exist infinitely many disjoint chaotic subsystems in this chaotic subsystem. Finally, Section 5 concludes this paper.

2. Preliminaries

For a finite symbol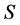, a word over 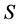is finite sequence 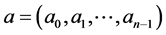of elements of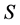. The length

of a is denoted by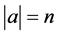. Denote the set of all words of length 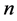by. If is a finite or infinite word

and is an interval of integers on which 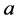is defined, put 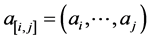and

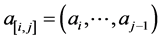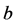. is a subword of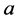, denoted by, if, for some interval; otherwise,

denoted. The set of bi-infinite configurations is denoted by and a metric “” on is defined as

, where, and is the metric on defined as

. It is well known that is a compact, perfect and totally disconnected metric

space.

By a theorem of Hedlund, a map is a cellular automata iff it is continuous and commutes with

shift map, i.e., , where is defined by. For any CA there exists

radius and a loca rule such that. Moreover, is a com- pact dynamical system. To enhance readability, it is desirable to write a CA as for local rule.

A set is -invariant if, and strongly -invariant if. If is closed

and -invariant, then or simply is called a subsystem of. For instance, let denote a set

of some finite words over, and is the set which consists of the bi-infinite configurations made up of all the words in. Then is subsystem of, where is said to be the determinative block system of

.

For bi-infinite ECA, and is denoted by. Each local rule can be expressed by a Boolean

function. For example, the Boolean function of rule 106 is,

, where “.”, “” and “?” stand for “AND”, “XOR” and “NOT” logical operations, respectively [11] .

Thus the global map of rule 106 is induced as follows: for any,

, , where denotes the th symbol of

. For clarity, the truth table of rule 106 is depicted in Table 1.

Based exclusively on this truth table, a subsystem of rule 106 in is shown as follows.

Proposition 1. For rule 106, there exists a subset such that iff,

, , where.

Proof: (Necessity) Suppose that there exists a subset such that, then,

, one has According to the Boolean function

of rule 106, one has this implies so and can

not be 1 simultaneously,. Additionally, if there exists such that then it

must satisfy that or, this is contradictory with Hence, the

determinative block system of is.

(Sufficiency) The proof of sufficiency can be verified directly, the details are omitted here. The proof of the proposition is completed.

For illustration, simulations of the spatial and temporal evolution of rule 106 with a random initial configuration and an initial configuration of are shown in Figure 1, where the black pixel stands for 1 and white for 0.

3. Complex Dynamics of

In this section, the dynamical behaviors of on are exploited. As the topological dynamics of a subshift of finite type is largely determined by the properties of its transition matrix, it is helpful to briefly review some

definitions from [17] . A matrix A is positive if all of its entries are nonnegative; irreducible if such

that; aperiodic if, such that. If is a 2-order subshift of finite type,

Table 1. Logical table of rule 106.

(a) (b)

Figure 1. (a) The evolution of rule 106 from random initial configuration, (b) The evolution of rule 106 from an initial configuration of.

then the associated transition matrix is the matrix with, if; otherwise.

Denote a 2-order subshift of finite type by It is known that a 2-order subshift of finite type is

topologically mixing if and only if its transition matrix is irreducible and aperiodic [17] [18] .

The nonlinear dynamical behavior of on is discussed by establishing the topologically conjugate

relationship between and a 2-order subshift of finite type. Let be a new symbolic

set, where, , represent the elements in, respectively. Then one can construct a new

symbolic space on. Denote by.

Then, the 2-order subshift of is defined by

. Moreover, it is clear to see that the transition

matrix A of the subshift is:

Theorem 1. 1) and are topologically conjugate;

2) is topologically mixing;

3) the topological entropy of satisfies, where is the spectral

radius of the transition matrix.

Proof: 1) Define a map from to as follows:

where. Then, it follows from the definition of that for any, one has

; namely,. Then, it is easily to check that is a homeomorphism and.

Hence, and are topologically conjugate.

2) satisfies; namely, is irreducible and aperiodic, which implies that is

topologically mixing on. Then, one can deduce is topologically mixing according to Theorem 1 1)

and Proposition 1.

3) As, where is the spectral radius of the transition matrix and

is the positive real root of. And and are topologically conjugate, so

.

It is noted that a positive topological entropy is an important signature of the complexity of the system. It follows from [18] that the positive topological entropy implies chaos in the sense of Li-Yorke. And the topologically mixing is a very complex property of dynamical systems. A system with topologically mixing property has many chaotic properties in different senses. Therefore, the above mathematical analysis provides the following result.

Theorem 2. 1) is chaotic in the sense of Li-Yorke;

2) is chaotic in the sense of both Li-Yorke and Devaney on.

4. Infinitely Many Chaotic subsystems of in

It is helpful to review some definitions and basic properties of releasing transformation before we discuss the

dynamics of on infinite number of subsystems. Let be a symbolic set, where

and represent new symbols, respectively, and

. Denote by the space of bi-infinite configurations over and induce a

matric “” onto as defined in the preceding section. Then, the releasing transformation R is defined as follows:

where

Proposition 2. [19] Releasing transformation is a continuous and injective map.

Let, , , and be a new sym- bolic set. Denote by the subshift in determined by the transition matrix as. Then induce, where is the classical left-shift map. And let be, then induce, where. Then considering and Proposition 1, one can easily obtain the following propo- sition.

Proposition 3. For each, is closed and -invariant.

Proposition 4. For each, and are topologically conjugate.

Proof: It is clear that the following diagram is commutative. The rest of proof can be completed by applying Proposition 2.

Theorem 3. For each, 1) is topologically mixing on each;

2) the topologically entropy of on equals to; therefore, the topologically entropy of

on equals to.

Proof: 1) It is clear to check that is irreducible and aperiodic, thus is topologically mixing on,

. For each, and are topologically conjugate, so is topologically

mixing on each and thus is topologically mixing on each based on Proposition 1 and Proposition

3.

2) Since, where is the the spectral radius of the transition

matrix,. Therefore, according to Proposition 3. Then the

topologically entropy of on each equals to; therefore, the topologically entropy of

on each equals to.

Theorem 4. For each, 1) is topologically mixing on;

2) is chaotic in the sense of both Li-Yorke and Devaney on.

Proof: 1) One can use the definition of the topologically mixing to prove that is topologically mixing

on each. i.e. for any two nonempty open subsets, , such that

. For each, the following are two conditions to illustrate:

Case 1.. According to theorem 3 (1), is topologically mixing, namely, for any two nonempty

open sets, , such that, so,.

Case 2.,. Firstly one need to prove that is a

homeomorphism. Since and is -invariant, then is surjective. Suppose that there exist

, such that, so, which implies, thus

. So is injective. Since is a compact Hausdorff space, is one to one, onto and

continuous map. exists and continuous. Therefore, is a homeomorphism. This

implies that is also an open set, thus, one has

, where.

2) It is easily deduced by Theorem 3 (2) and Theorem 4 (1).

Note that, where,. Let

, then. Observe that, then for each, is

closed and -invariant. Thus Theorem 3 and 4 also hold for, where.

Remark 1. It is important to point out that the topologically entropy of on approaches 0 as approaches. Meanwhile, it has been proved that there exists a “big” subsystem of rule 106, including

infinite disjoint chaotic subsystems. This analytical assertion provides an enlightening fact that the

hyper Bernoulli-shift rule 106 is full of infinite “small” chaotic subsystems in a “big” subsystem, demonstrating its very rich and complex dynamics.

5. Conclusion

One of the main challenges is to explore the quantitative dynamics in cellular automata evolution. Hyper Bernoulli-shift rules possess very interesting and complicated dynamical behaviors [19] [20] , for example, rule 180 possesses infinitely many generalized sub-shifts [20] [21] . This paper is devoted to an in-depth study of cellular automaton rule 106 in the framework of symbolic dynamics. Indeed, rule 106 actually is topologically mixing and possesses positive topological entropy on a subsystem. Furthermore, in this chaotic subsystem, rule 106 defines infinitely number of chaotic subsystems with rich and complex dynamical behaviors, such as topologically mixing, positive topological entropies and chaos in the sense of Li-Yorke and Devaney. Although in this work, one obtains some interesting results, to rule 106, it still needs much deeper research in the future.

Acknowledgements

This research was supported by the NSFC (Grant No. 11171084).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	von Neumann, J. and Burks, A.W. (1966) Theory of Self-Reproducing Automata. University of Illinois Press, Urbana and London.
[2]	Hedlund, G.A. (1969) Endomorphisms and Automorphism of the Shift Dynamical System. Theory of Computing Systems, 3, 320-375.
[3]	Gardner, M. (1970) The Fantastic Combinations of John Conway’s New Solitaire Game Life. Scientific American, 223, 120-123. http://dx.doi.org/10.1038/scientificamerican1070-120
[4]	Wolfram, S. (1984) Universality and Complexity in Cellular Automata. Physica D, 10, 1-35. http://dx.doi.org/10.1016/0167-2789(84)90245-8
[5]	Wolfram, S. (1986) Theory and Application of Cellular Automata. Word Scientific, Singapore.
[6]	Wolfram, S. (2002) A New Kind of Science. Wolfram Media, Inc., Champaign.
[7]	Chua, L.O., Sbitnev, V.I. and Yoon, S. (2004) A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Science, Part III: Predicting the Unpredictable. International Journal of Bifurcation and Chaos, 14, 3689-3820. http://dx.doi.org/10.1142/S0218127404011764
[8]	Chua, L.O., Guan, J., Sbitnev, V.I. and Jinwook, S. (2007) A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Science, Part VII: Isles of Eden. International Journal of Bifurcation and Chaos, 17, 2839-3012. http://dx.doi.org/10.1142/S0218127407019068
[9]	Chua, L.O., Karacs, K., Sbitnev, V.I., Guan, J. and Jinwook, S. (2007) A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Science, Part VIII: More Isles of Eden. International Journal of Bifurcation and Chaos, 17, 3741-3894. http://dx.doi.org/10.1142/S0218127407019901
[10]	Chua, L.O. and Pazienza, G.E. (2010) A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Science, Part XIV: More Bernoulli -Shift Rules. International Journal of Bifurcation and Chaos, 20, 2253-2425. http://dx.doi.org/10.1142/S0218127410027155
[11]	Guan, J.B., Shen, S.W., Tang, C.B. and Chen, F.Y. (2007) Extending Chua’s Global Equivalence Theorem on Wolfram’s New Kind of Science. International Journal of Bifurcation and Chaos, 17, 4245-4259. http://dx.doi.org/10.1142/S0218127407019925
[12]	Chen, F.Y., Jin, W.F., Chen, G.R., Chen, F.F. and Chen, L. (2009) Chaos of Elementary Cellular Automata Rule 42 of Wolfram’s Class II. Chaos, 19, Article ID: 013140.
[13]	Chen, F.Y., Chen, G. and Jin, W.F. (2013) Transitivity and Chaoticity in 1-D Cellular Automata. International Journal of Modern Nonlinear Theory and Application, 2, 69-73. http://dx.doi.org/10.4236/ijmnta.2013.21A008
[14]	Jin, W.F., Chen, F.Y., Chen, G.R., Chen, L. and Chen, F.F. (2010) Extending the Symbolic Dynamics of Chua’s Bernoulli-Shift Rule 56. Journal of Cellular Automata, 5, 121-138.
[15]	Chen, G.R., Chen, F.Y., Guan, J.B. and Jin, W.F. (2010) Symbolic Dynamics of Some Bernoullif-Shift Cellular Automata Rules. 2010 International Symposium on Nonlinear Theory and Its Applications, 595-598.
[16]	Cattaneo, G., Finelli, M. and Margara, L. (2000) Investigating Topological Chaos by Elementary Cellular Automata Dynamics. Theoretical Computer Science, 244, 219-241. http://dx.doi.org/10.1016/S0304-3975(98)00345-4
[17]	Kitchens, B. (1998) Symbolic Dynamics: One-Sided, Two-Sided and Countable State Markov Shifts. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-58822-8
[18]	Blanchard, F., Glasner, E. and Kolyada, S. (2002) On Li-Yorke Pairs. Journal fur reine und angewandte Mathematik, 547, 51-68.
[19]	Jin, W.F. and Chen, F.Y. (2011) Topological Chaos of Universal Elementary Cellular Automata Rule. Nonlinear Dynamics, 63, 217-222. http://dx.doi.org/10.1007/s11071-010-9798-z
[20]	Chen, W., Chen, F.Y., Bian, Y.F. and Chen, J. (2011) Infinite Number of Chaotic Generalized Sub-Shifts of Cellular Automaton Rule 180. 2011 International Conference on Scientific Computing, 226-230.
[21]	Cattaneo, G. and Margara, L. (1998) Generalized Sub-Shifts in Elementary Cellular Automata: The “Strange Case” of Chaotic Rule 180. Theoretical Computer Science, 201, 171-187. http://dx.doi.org/10.1016/S0304-3975(97)00210-7