A Trading Execution Model Based on Mean Field Games and Optimal Control ()
1. Introduction
In recent years technology innovation, deregulation policies and ubiquitous availability of Internet connections have determined the emergence of new forms of trading in the financial markets. These forms of trading give the possibility to the investor of operating in the market without the help of traditional brokers and offer the opportunity of using huge data sets and sophisticated mathematical models to support investment decisions. Automated trading tools, sometimes called algorithmic trading tools, have been developed to support the investors in their decision process and to execute their orders. We restrict our attention to the algorithmic trading tools used to determine trading execution strategies. Algorithmic trading tools are available even to retail investors, however the interest in finding how to execute orders involving large blocks of shares is limited to institutional investors, such as banks, insurance companies, mutual funds, and to very wealthy individuals. We refer to these investors as big traders and to their orders as large orders. The execution of large orders influences market prices, while the execution of the orders of a retail trader does not affect market prices. This is due to the limited size of these orders. The retail traders influence market prices only through their collective behaviour. Ad hoc algorithmic trading tools have been developed to determine the trading execution strategies of large orders. In this paper we present a mathematical model that can be used to build one of these tools.
Many authors have addressed the problem of modeling the behaviour of a big trader and of the asset share price during the execution of a large order. Usually it is assumed that the trading execution strategies of large orders satisfy the following conditions: 1) maximization of the revenue resulting from the order execution (or minimization of the trading cost), 2) minimization of the risk deriving from possible delays in the order execution. These two goals can be conflicting and in many circumstances it is necessary to find a compromise between them. Usually the models developed to determine the execution strategies of large orders do not consider explicitly the presence in the market of retail traders. The only trading activity studied in these models is the trading activity of the big trader. In fact the models synthesize the behaviour of the market (including the behaviour of the retail traders) in the asset share price dynamic equation. This last equation describes the “asset share price in absence of trading” and the effect on the asset share price of the trading activity of the big trader. The expression “asset share price in absence of trading” sounds strange, however it is of common use and means: the asset share price determined by the trading activity that is not studied explicitly in the model. Let us discuss briefly the scientific literature on this subject.
In 1998 Bertsimas and Lo [1] presented a discrete time trading model describing a trader that must buy a block of asset shares in an assigned time interval minimizing the expected value of the trading cost. The asset share price is modeled as a discrete arithmetic random walk that depends linearly from the number of asset shares bought/sold by the trader. This linear term models the permanent market impact on the asset share price of the trading activity of the big trader. In [1] the problem of determining the order optimal trading execution strategy is modeled as a dynamic optimization problem.
In 2000 Almgren and Chriss [2] introduced a discrete time trading model and considered the situation where a trader must liquidate an initial holding of an asset in an assigned time interval. The trading cost is defined as the difference between the value of the initial holding at the time when the order execution begins and the final revenue for the trader at the end of the order execution. In [2] it is assumed that the trader acts minimizing the expected value of the trading cost subject to a constraint on the variance of the trading cost. Moreover it is assumed that the dynamics of the asset share price depends on the number of shares sold by the trader. In fact the dynamics of the asset share price is modeled as a discrete arithmetic random walk that depends linearly from the average trading rate of the trader. This linear term represents the instantaneous market impact of the trading activity of the big trader on the asset share price. The optimal trading execution strategy of the trader is the solution of a mean variance optimization problem. In [3] Almgren has extended the results presented in [2] to the continuous time case and has modeled the instantaneous market impact of the trading activity of the big trader on the asset share price as a nonlinear function of the trading rate. Moreover in [3] the asset share price dynamics is modeled as an arithmetic random walk whose variance depends from the trading rate. In some special cases explicit formulae for the resulting optimal trading execution strategies are found. In [4] a stochastic version of the problem studied in [3] is considered.
Gatheral and Schied [5] modified the model discussed in [4] considering as cost functional of the control problem studied the expected value of the sum of the trading cost and of a time averaged “value at risk” associated to the trading execution strategy. The robustness of the model presented in [5] is established in [6] .
In [7] Ankirchner, Blanchet Scalliet and Eyraud Loisel proposed a variant of the stochastic trading execution model studied in [4] and [5] . They assumed that the Brownian motion that describes the asset share price dynamics in absence of trading has a non zero drift and that the trading rate of the big trader is a square integrable stochastic process. The drift term of the asset share price dynamics can be interpreted as the directional view of the trader about the asset share price (i.e. the bullish or bearish attitude of the trader about the asset share price). This drift term is assumed to be a linear function of the asset share price. The optimal trading execution strategy solution of the model proposed in [7] is a Gaussian process that becomes a deterministic function of time when the drift term of the asset share price dynamics is constant.
In the papers mentioned above (with the exception of [1] ) given the order of buying or selling a certain number of asset shares in an assigned time interval the problem of determining the corresponding optimal trading execution strategy is reduced to a dynamic optimization problem or to an optimal control problem. The control variable of these problems is the trading rate of order execution. Sometimes the trading rate is called rhythm of the order execution. In the previous models the optimal trading rate is determined without considering explicitly the transactions volume on the asset shares during the order execution. However it is easily understood that in the reality of the financial markets the impact of a trade on the asset share price depends from the transactions volume on the asset share during the trade. Guéant in [8] is the first author that considers the dependence of the optimal trading rate from the transactions volume. He assumes that the trading rate of the trader is proportional to the transactions volume and that the transactions volume is a continuous deterministic function of time. In this case the control variable of the model is the proportionality factor between the trading rate of the trader and the transactions volume on the asset share (i.e. the fraction of the transactions volume generated by the trader) as a function of time. This proportionality factor is called participation rate of the trader to the (asset shares) market. The model studied in [8] considers as utility function the expected value of the Constant Absolute Risk Aversion (CARA) function. The CARA function is the exponential of the final revenue minus the final cost of the trade. Finally in [9] Guéant introduces a model that can substitute Almgren’s model [3] . In this model the trading execution strategy is a Poisson process whose intensity depends from the transactions volume.
In this paper we study a market consisting of one traded asset where a multitude of retail traders and a big trader operate. The big trader executes large orders. The retail traders are investors that belong to a population of individuals having the following features: aversion to the risk of holding open positions on the asset shares, desire to behave like the other retail traders, desire to avoid abrupt changes in trading strategies and desire to have in the long run a given position on the asset shares. The trading position of a retail trader is the number of asset shares held by the retail trader. The behaviour of a retail trader on the market is described by its trading position as a function of time. We assume that only the trading position of the entire population of the retail traders contributes with its mean value to determine the asset share price. This is due to the fact that individually the retail traders execute orders of limited size that do not influence the asset share price. We adopt a mean field game model to describe the behaviour of the retail traders. That is the (time) dynamics of the individual trading positions of the retail traders is substituted with a “mean dynamics” satisfied by the trading position of a “mean retail trader”. This “mean dynamics” is defined by the mean field equation of the mathematical model of the dynamics of the individual trading positions of the retail traders. In this way the problem of modeling the behaviour of the retail traders is greatly simplified. In fact instead of a multitude of equations necessary to describe the trading positions of the retail traders individually in the mean field game model we use only one “mean field equation” that describes the trading position of the “mean retail trader”. That is the behaviour of the retail traders is described using a mean field game model. The mean field game models have been introduced by Lasry and Lions in [10] . These models have been used in many contexts to study populations of interacting rational agents. For example pedestrian crowds [11] , exhaustible resources productions [12] , technical innovation processes [13] and supply demand equilibrium prices of assets [14] or of commodities [15] have been studied using mean field game models. A wide review of problems that can be approached using this type of models is contained in [16] . The mean field game model that describes the behaviour of the retail traders uses as control variable the trading rate of the retail traders (in the “mean field” approximation). The utility function of this model is the sum of four terms. The first term expresses the fact that the retail traders want to adopt similar strategies and depends from the probability distribution of the trading position of the retail traders (in the “mean field” approximation). The second term expresses the fact that the retail traders try to avoid abrupt changes of their trading strategies and depends from the trading rate of the retail traders (in the “mean field” approximation). The third term expresses the fact that the retail traders try to avoid the risk associated to the fact of having open positions on the asset shares and depends from the number of asset shares held by the retail traders as a function of time (in the “mean field” approximation). The fourth term expresses the fact that in the long run the retail traders want to have a given position on the asset shares and depends from the number of asset shares held by the retail traders at the final time of the game (in the “mean field” approximation). The stochastic differential equation that defines the dynamics of the trading position of the retail traders (in the “mean field” approximation) and its initial condition are the constraints of the mean field game model studied. To simplify the exposition from now on instead of specifying retail traders in the “mean field approximation” we will simply say retail traders without specification. The mean field game model that describes the behaviour of the retail traders is studied using the dynamic programming principle. The first order necessary optimality condition of this model is a system of partial differential equations made of the Hamilton Jacobi Bellman equation satisfied by the value function of the mean field game and of the forward Kolmogorov equation satisfied by the probability density function of the trading position of the retail traders. The condition that establishes the relation between the optimal trading rate and the value function of the game couples these two partial differential equations. This system of partial differential equations is equipped with an initial and a final condition. The solution of this problem determines the optimal trading execution strategy of the retail traders. Under some assumptions, following Kalman [17] it is possible to reduce the problem of solving the system of partial differential equations mentioned above to the problem of solving a constrained two point boundary value problem for a system of six Riccati ordinary differential equations. Explicit and numerical solutions of this constrained two point boundary value problem are studied.
Let us turn our attention to the behaviour of the big trader. To fix the ideas we study the liquidation problem, that is the problem of executing the order of selling a (large) number of asset shares in a prescribed time interval. It is easy to see how to rephrase the solution of the liquidation problem presented later to consider the problem of buying a (large) number of shares in a prescribed time interval. The goal pursued by the big trader is to sell a given block of asset shares in the time interval assigned maximizing the expected value of the revenue resulting from the sale. The big trader pursues this goal choosing its trading rate as a function of time. That is the trading rate is the control variable of the optimal control problem that describes the behaviour of the big trader. At any given time the instantaneous revenue of the sale is the product of the asset share price times the number of shares sold at that time. The revenue of the sale is the integral in time of the instantaneous revenue over the time interval assigned to execute the trade. As already said the asset share price is described by the asset share price dynamic equation. Let us discuss briefly this last equation. This equation couples the mathematical models that describe the retail traders and the big trader. In absence of trading the asset share price dynamics is assumed to be an arithmetic Brownian motion. The trading activity generated by the retail traders and/or by the big trader influences the asset share price. For example as expected when the big trader and the “majority” of the retail traders are buyers the asset share price tends to increase, conversely when the big trader and the “majority” of the retail traders are sellers the asset share price tends to decrease. Mathematically these intuitive facts are modeled with a simple generalization of the asset share price dynamic equation introduced by Almgren in [3] . We assume that the asset share price is the sum of four terms, that is: the asset share price in absence of trading, the instantaneous impact factor of the trading activity of the retail traders, the instantaneous impact factor of the trading activity of the big trader and the permanent impact factor of the trading activity of the big trader. The instantaneous impact factor of the trading activity of the retail traders is assumed to be proportional to the expected value of their trading execution rate. This last term is not present in the asset share price dynamic equation used in [3] . The remaining three terms of the asset share price dynamic equation of our model are already present in the asset price equation used in [3] . Note that the assumption that the asset share price depends from the trading execution strategy of the retail traders and the choice made of the big trader objective function imply that the behaviour of the big trader depends from the behaviour of the retail traders. That is in order to find the optimal trading execution strategy of the big trader it is necessary first to solve the mean field game model associated to the retail traders to determine their optimal trading execution strategy. In our model the dependence of the behaviour of the retail traders from the trading activity of the big trader is not considered. In fact it is reasonable to assume that in many circumstances the retail traders are not aware of the trading activity of the big trader. The problem of determining the optimal trading execution strategy of the big trader is translated in a linear quadratic optimal control problem whose control variable is the trading rate of the big trader and whose utility function is the final revenue of the trade. The solution of the Hamilton Jacobi Bellman equation associated to this optimal control problem is reduced [17] to the solution of a system of Riccati ordinary differential equations with a final condition. Under some hypotheses an explicit formula for the optimal trading execution strategy of the big trader is derived. Finally we present an extensive numerical study of the trading execution model developed. This numerical study shows several interesting facts. In particular the study shows that the mean field game model considered provides a setting where different kinds of retail traders can be represented. For example we show that retail traders classified in the jargon of the financial markets as “buy and hold investors” or as “short term investors” can be represented in the model. For the convenience of the reader let us recall the meaning of these expressions. The buy and hold investors are investors that buy and then hold the asset bought for a long time period betting on the increment of the asset value due to its fundamentals. These investors do not like to change their positions in the market regardless of the market fluctuations. Conversely the short term investors are investors that open and close their positions within a relatively short time period to exploit movements of the asset share price. The short term investors do not like the risk associated to the fact of having open positions on the asset shares. Their different behaviours determine different effects on the asset share price dynamics. It follows that the optimal trading execution strategy of the big trader changes as a consequence of the fact that the retail traders are buy and hold investors or are short term investors. Several numerical examples are studied in detail to show the versatility of the model presented.
The interested reader is referred to the website: http://www.econ.univpm.it/recchioni/finance/w19 to find material including animations, an interactive application and an app that helps the understanding of the paper. A general reference to the work of the authors and of their coauthors in mathematical finance is the website: http://www.econ.univpm.it/recchioni/finance.
The paper is organized as follows. In Section 2 we define the trading execution model studied, that is we define the mean field game model associated to the retail traders, the asset share price dynamic equation and the optimal control problem associated to the big trader. In Section 3 we solve the mean field game model. In Section 4 we solve the optimal control problem. In Section 5 we present a numerical study of the trading execution model developed in Sections 2, 3 and 4.
2. The Trading Execution Model
Let 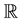 be the set of real numbers,
be the set of real numbers, 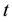 be a real variable that denotes time and
be a real variable that denotes time and  be a positive number. We assume that
be a positive number. We assume that  is the time horizon of the mean field game model that describes the behaviour of the retail traders. This means that the mean field game model is solved for
is the time horizon of the mean field game model that describes the behaviour of the retail traders. This means that the mean field game model is solved for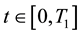 . Let us consider a state variable
. Let us consider a state variable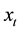 ,
, 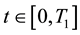 , that represents the number of asset shares held by the retail traders at time
, that represents the number of asset shares held by the retail traders at time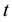 ,
,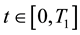 . The variable
. The variable 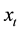 is called trading position of the retail traders at time
is called trading position of the retail traders at time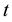 ,
, 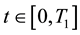 , and is a real stochastic process. Positive values of
, and is a real stochastic process. Positive values of 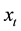 mean that the retail traders have a long position on the asset shares at time
mean that the retail traders have a long position on the asset shares at time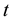 , negative values of
, negative values of 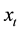 mean that the retail traders have a short position on the asset shares at time
mean that the retail traders have a short position on the asset shares at time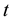 ,
,![]() . Recall that when we write retail traders we always mean retail traders in the “mean field approximation”. We assume that the stochastic process
. Recall that when we write retail traders we always mean retail traders in the “mean field approximation”. We assume that the stochastic process![]() ,
, ![]() , satisfies the following stochastic differential equation:
, satisfies the following stochastic differential equation:
![]() , (1)
, (1)
with initial condition:
![]() , (2)
, (2)
where ![]() is a continuous function,
is a continuous function, ![]() is a real constant,
is a real constant, ![]() ,
, ![]() , is a standard Wiener process such that
, is a standard Wiener process such that ![]() and
and![]() ,
, ![]() , is its stochastic differential. The initial condition
, is its stochastic differential. The initial condition ![]() is a known random variable whose probability density function is denoted with
is a known random variable whose probability density function is denoted with![]() ,
,![]() . We have
. We have
![]() ,
, ![]() , and
, and![]() . We assume that the initial value problem (1), (2) has a unique solution
. We assume that the initial value problem (1), (2) has a unique solution
when![]() . The function
. The function ![]() that appears in (1) is the trading rate of the retail traders and is the control variable of the mean field game model considered. Equation (1) is the “mean field equation” announced in the Introduction that defines the dynamics of the trading position of the “mean retail trader” that is used to describe the multitude of the retail traders in the “mean field approximation”.
that appears in (1) is the trading rate of the retail traders and is the control variable of the mean field game model considered. Equation (1) is the “mean field equation” announced in the Introduction that defines the dynamics of the trading position of the “mean retail trader” that is used to describe the multitude of the retail traders in the “mean field approximation”.
For ![]() we denote with
we denote with![]() ,
, ![]() , the probability density function of the random variable
, the probability density function of the random variable ![]() solution of (1), (2). The function
solution of (1), (2). The function![]() ,
, ![]() ,
, ![]() , satisfies the forward Kolmogorov equation associated to (1):
, satisfies the forward Kolmogorov equation associated to (1):
![]() , (3)
, (3)
with the initial condition implied by (2):
![]() . (4)
. (4)
Recall that in (3) the function ![]() is not a known coefficient,
is not a known coefficient, ![]() is the control variable that must be determined as solution of the mean field game model. The fact that
is the control variable that must be determined as solution of the mean field game model. The fact that ![]() is a probability density function implies that the function
is a probability density function implies that the function ![]() solution of (3), (4) is a probability density function as a function of
solution of (3), (4) is a probability density function as a function of ![]() for
for ![]() that
that
is implies that:![]() ,
, ![]() ,
, ![]() , and
, and![]() ,
,![]() .
.
Let ![]() denote the expected value of
denote the expected value of ![]() and
and ![]() be the set of the square integrable processes on
be the set of the square integrable processes on ![]()
This means that the real stochastic process![]() ,
, ![]() , belongs to
, belongs to ![]() if and only if
if and only if ![]()
Let![]() ,
, ![]() , be the trading rate of Equation (1) we assume that
, be the trading rate of Equation (1) we assume that![]() . Given the real parameters
. Given the real parameters![]() ,
, ![]() and
and ![]() we consider the following problem:
we consider the following problem:
![]() , (5)
, (5)
where:
![]() (6)
(6)
subject to the constraints (1)-(4). The model (5), (6), (1)-(4) is the mean field game model used to describe the behaviour of the retail traders. This means that the retail traders adopt the trading execution strategy![]() ,
,![]() , whose rate
, whose rate ![]() is the solution of problem (5), (6), (1)-(4). The parameter
is the solution of problem (5), (6), (1)-(4). The parameter ![]() is called risk aversion parameter. Note that the constraints (3), (4) are consequences of the constraints (1), (2) and that they can be omitted when (1), (2) are imposed. However we prefer to mention (3), (4) explicitly in the statement of the previous problem in order to emphasize the role of
is called risk aversion parameter. Note that the constraints (3), (4) are consequences of the constraints (1), (2) and that they can be omitted when (1), (2) are imposed. However we prefer to mention (3), (4) explicitly in the statement of the previous problem in order to emphasize the role of![]() ,
, ![]() ,
, ![]() , in the functional
, in the functional![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , defined in (6). The functional
, defined in (6). The functional![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , is
, is
called utility function or cost functional of the mean field game model and is the sum of four terms. The first one: ![]() expresses the fact that the retail traders want to behave in a similar way, the second one:
expresses the fact that the retail traders want to behave in a similar way, the second one: ![]() expresses the fact that the retail traders try to avoid abrupt changes of their trading strategies, the third one:
expresses the fact that the retail traders try to avoid abrupt changes of their trading strategies, the third one: ![]() expresses the fact that the retail traders do not like the risk associated to the fact of having open positions on the asset shares, and the fourth one:
expresses the fact that the retail traders do not like the risk associated to the fact of having open positions on the asset shares, and the fourth one: ![]() expresses the fact that in the
expresses the fact that in the
long run (that is at time![]() ) the retail traders want to have a given position on the asset shares (that is the position
) the retail traders want to have a given position on the asset shares (that is the position![]() ). The choice of the term
). The choice of the term![]() ,
, ![]() , in (6) instead of a more general term such as, for example,
, in (6) instead of a more general term such as, for example, ![]() ,
, ![]() , with
, with![]() ,
, ![]() , a suitable (real valued) function, is essential in Section 3 to solve elementarily the mean field game model (5), (6), (1)-(4) when
, a suitable (real valued) function, is essential in Section 3 to solve elementarily the mean field game model (5), (6), (1)-(4) when![]() ,
, ![]() , is a Gaussian probability density function. Note that in the utility function
, is a Gaussian probability density function. Note that in the utility function![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , the
, the
terms![]() ,
, ![]() ,
, ![]() , and
, and ![]() depend from the control variable
depend from the control variable ![]() through the
through the
Equations (1), (3).
Now let us discuss the mathematical model that describes the behaviour of the big trader. Let ![]() be a positive number such that
be a positive number such that ![]() and
and ![]() be a positive integer that represents the number of asset shares held by the big trader at time
be a positive integer that represents the number of asset shares held by the big trader at time![]() . We consider the problem of determining the optimal trading execution strategy that implements the order of selling
. We consider the problem of determining the optimal trading execution strategy that implements the order of selling ![]() asset shares in the time interval
asset shares in the time interval![]() . This order is called liquidation order since consists in the order of liquidating the position on the asset shares held by the big trader at time
. This order is called liquidation order since consists in the order of liquidating the position on the asset shares held by the big trader at time ![]() in the time interval
in the time interval![]() . Let
. Let![]() ,
, ![]() , be the number of asset shares held by the big trader at time
, be the number of asset shares held by the big trader at time![]() ,
,![]() . We assume that
. We assume that![]() ,
, ![]() , is solution of the following differential equation:
, is solution of the following differential equation:
![]() , (7)
, (7)
with initial condition:
![]() , (8)
, (8)
and final condition:
![]() , (9)
, (9)
where in (7) ![]() is a continuous function that represents the trading rate of the big trader. Note that the differential Equation (7), that describes the dynamics of the trading strategy of the big trader, is the equation used by Almgren [3] in similar circumstances. We assume that the initial value problem (7) (8) has a unique solution in the time interval
is a continuous function that represents the trading rate of the big trader. Note that the differential Equation (7), that describes the dynamics of the trading strategy of the big trader, is the equation used by Almgren [3] in similar circumstances. We assume that the initial value problem (7) (8) has a unique solution in the time interval![]() . The function
. The function![]() ,
, ![]() is the control variable of the control problem that defines the behaviour of the big trader. The function
is the control variable of the control problem that defines the behaviour of the big trader. The function![]() ,
, ![]() is the trading execution strategy of the big trader. The quantities
is the trading execution strategy of the big trader. The quantities ![]() and
and ![]() are respectively the trading rate and the selling rate of the trading execution strategy
are respectively the trading rate and the selling rate of the trading execution strategy ![]() at time
at time![]() ,
,![]() . Let
. Let ![]() be the set of the square integrable functions defined on
be the set of the square integrable functions defined on ![]() and
and ![]() be the set of the functions
be the set of the functions![]() ,
, ![]() , solution of (7)-(9) whose derivative
, solution of (7)-(9) whose derivative![]() ,
, ![]() , belongs to
, belongs to![]() . We assume that
. We assume that![]() . The set
. The set ![]() is the set of the admissible trading execution strategies of the optimal control problem that defines the behaviour of the big trader. Let us define the utility function of the control problem that determines the behaviour of the big trader. This is done introducing the asset share price dynamic equation.
is the set of the admissible trading execution strategies of the optimal control problem that defines the behaviour of the big trader. Let us define the utility function of the control problem that determines the behaviour of the big trader. This is done introducing the asset share price dynamic equation.
We use as asset share price dynamic equation a simple generalization of the equation introduced by Almgren in [3] . Let ![]() be the asset share price at time
be the asset share price at time![]() ,
, ![]() , we assume that
, we assume that![]() ,
, ![]() is a real stochastic process defined as follows:
is a real stochastic process defined as follows:
![]() , (10)
, (10)
![]() , (11)
, (11)
where![]() ,
, ![]() , and
, and![]() ,
, ![]() ,
, ![]() are positive constants.
are positive constants.
Moreover we assume that:![]() ,
, ![]() , where
, where ![]() is a real constant,
is a real constant, ![]() is a positive random variable,
is a positive random variable, ![]() ,
, ![]() , is a standard Wiener process defined in the time interval
, is a standard Wiener process defined in the time interval ![]() such that
such that ![]() and
and![]() ,
, ![]() , is its stochastic differential. We assume that
, is its stochastic differential. We assume that![]() ,
, ![]() ,
, ![]() ,
, ![]() , are independent. The term
, are independent. The term![]() ,
, ![]() , represents the asset share price in absence of trading. Note that with the previous choices the asset share price in absence of trading
, represents the asset share price in absence of trading. Note that with the previous choices the asset share price in absence of trading![]() ,
, ![]() , and the asset share price (in presence of trading)
, and the asset share price (in presence of trading)![]() ,
, ![]() , can be negative. Usually this is considered an undesirable property, however when sufficiently small values of
, can be negative. Usually this is considered an undesirable property, however when sufficiently small values of ![]() are considered it can be tolerated, see [3] [5] . In fact in this case from the assumption
are considered it can be tolerated, see [3] [5] . In fact in this case from the assumption ![]() with probability one it follows that the probability of having negative prices in the time interval
with probability one it follows that the probability of having negative prices in the time interval ![]() is small and can be made arbitrarily small taking
is small and can be made arbitrarily small taking ![]() small enough. The asset share price dynamic equation of Almgren’s model [3] is obtained from (10) choosing
small enough. The asset share price dynamic equation of Almgren’s model [3] is obtained from (10) choosing ![]() and has the same undesired property of (10). The terms
and has the same undesired property of (10). The terms ![]() and
and ![]() represent respectively the instantaneous market impact at time
represent respectively the instantaneous market impact at time![]() ,
, ![]() , of the trading activity of the retail traders and of the big trader. The term
, of the trading activity of the retail traders and of the big trader. The term ![]() represents the permanent market impact at time
represents the permanent market impact at time![]() ,
, ![]() , of the trading activity of the big trader. The choice of the term
, of the trading activity of the big trader. The choice of the term![]() ,
, ![]() , to model the effect on the asset share price of the trading activity of the retail traders reflects the assumptions stated in the Introduction. In fact in the Introduction we have assumed that individually the retail traders execute small orders that do not influence the asset share price, these orders influence the asset share price only through the expected value of their trading rates, that is through the term
, to model the effect on the asset share price of the trading activity of the retail traders reflects the assumptions stated in the Introduction. In fact in the Introduction we have assumed that individually the retail traders execute small orders that do not influence the asset share price, these orders influence the asset share price only through the expected value of their trading rates, that is through the term![]() ,
,![]() . Note that the expected value of the trading rate of the mean retail trader
. Note that the expected value of the trading rate of the mean retail trader![]() ,
, ![]() , can be imagined as being proportional to the expected value of the trading rate of the multitude of the retail traders. The situation is different for the big trader. The big trader executes large orders and the trading rate
, can be imagined as being proportional to the expected value of the trading rate of the multitude of the retail traders. The situation is different for the big trader. The big trader executes large orders and the trading rate![]() ,
, ![]() , of a large order influences the asset share price directly. In (10) this influence is modeled through the terms
, of a large order influences the asset share price directly. In (10) this influence is modeled through the terms ![]() and
and![]() ,
,![]() .
.
Let![]() ,
, ![]() , be a trading execution strategy that satisfies (7)-(9). It is easy to see that when the big trader adopts the trading execution strategy
, be a trading execution strategy that satisfies (7)-(9). It is easy to see that when the big trader adopts the trading execution strategy![]() ,
, ![]() , and the asset share price dynamics is described by (10), (11) the expected final revenue (i.e. the expected revenue at time
, and the asset share price dynamics is described by (10), (11) the expected final revenue (i.e. the expected revenue at time![]() ) for the big trader resulting from the sale of
) for the big trader resulting from the sale of ![]() asset shares in the time interval
asset shares in the time interval ![]() is:
is:
![]() . (12)
. (12)
Let us take a closer look to (12). Integrating (12) by parts and using (7) we have:
![]() . (13)
. (13)
Note that the assumption ![]() implies that when
implies that when ![]() the expression
the expression
![]() is well defined and finite. From (13) we have:
is well defined and finite. From (13) we have:
![]() . (14)
. (14)
The optimal trading execution strategy of the big trader is the strategy that maximizes the expected final revenue of the big trader (14) subject to the constraints (7)-(9). That is the problem of finding the optimal trading execution strategy of the big trader consists in solving the following optimal control problem:
![]() , (15)
, (15)
where:
![]() , (16)
, (16)
subject to the constraints (7)-(9). Note that in (16) we have dropped the term ![]() that appears in
that appears in
(14). In fact this term does not depend from the control variable ![]() and can be dropped from the objective function (14) without changing the solution of the control problem considered. The optimal control problem (15), (16), (7)-(9) is a linear quadratic optimal control problem. For later convenience note that the utility function
and can be dropped from the objective function (14) without changing the solution of the control problem considered. The optimal control problem (15), (16), (7)-(9) is a linear quadratic optimal control problem. For later convenience note that the utility function![]() ,
, ![]() , defined in (16) does not depend from
, defined in (16) does not depend from ![]() and that the presence of
and that the presence of![]() ,
, ![]() in (16) determines how the behaviour of the retail traders influences the behaviour of the big trader.
in (16) determines how the behaviour of the retail traders influences the behaviour of the big trader.
3. The Optimal Trading Execution Strategy of the Retail Traders
Let us consider the mean field game problem (5), (6), (1)-(4). We define:
![]() , (17)
, (17)
to be the value function of problem (5), (6), (1)-(4).
The function![]() ,
, ![]() ,
, ![]() , defined in (17), satisfies the following Hamilton Jacobi Bellman equation:
, defined in (17), satisfies the following Hamilton Jacobi Bellman equation:
![]() , (18)
, (18)
with final condition:
![]() , (19)
, (19)
where ![]() is the Hamiltonian function of the mean field games (5), (6), (1)-(4).
is the Hamiltonian function of the mean field games (5), (6), (1)-(4).
Therefore the optimal trading execution strategy of the retail traders can be determined solving the following system of partial differential equations, see [10] :
![]() , (20)
, (20)
![]() , (21)
, (21)
where the function![]() ,
, ![]() ,
, ![]() , must satisfy the condition
, must satisfy the condition![]() ,
, ![]() ,
,![]() . This last condition couples the Equations (20), (21). The system (20), (21) with the condition
. This last condition couples the Equations (20), (21). The system (20), (21) with the condition![]() ,
, ![]() ,
, ![]() , is equipped with a final condition on
, is equipped with a final condition on ![]() in
in ![]() and an initial condition on
and an initial condition on ![]() in
in ![]() that is:
that is:
![]() , (22)
, (22)
![]() . (23)
. (23)
Equations (20), (21) with the conditions![]() ,
, ![]() ,
, ![]() , (22), (23) are a system of nonlinear
, (22), (23) are a system of nonlinear
partial differential equations with an initial and a final condition. This system expresses the first order necessary optimality condition of the mean field game model (5), (6), (1)-(4). Once known the solution of this system of partial differential equations the optimal trading rate of the retail traders solution of problem (5), (6), (1)-(4) is
determined by the condition:![]() ,
, ![]() where
where![]() ,
, ![]() is the solution of (1), (2) when
is the solution of (1), (2) when ![]() is chosen equal to
is chosen equal to![]() .
.
We look for elementary solutions of problem (20), (21) with the conditions![]() ,
, ![]() ,
, ![]() ,
,
(22), (23). In analogy with the work of Kalman [17] we formulate some hypotheses that make possible to reduce
the solution of problem (20), (21) with the conditions![]() ,
, ![]() ,
, ![]() , (22), (23) to the solution of
, (22), (23) to the solution of
a constrained two point boundary value problem for a system of six Riccati ordinary differential equations. The choice of the logarithm function in the first addendum of (6) and as a consequence the presence of the logarithm function on the right hand side of (20) are crucial to operate this reduction.
Let ![]() be a random variable and let
be a random variable and let ![]() be the Gaussian probability distribution of mean
be the Gaussian probability distribution of mean ![]() and standard deviation
and standard deviation![]() . The notation
. The notation ![]() means that the random variable
means that the random variable ![]() is distributed
is distributed![]() .
.
We have:
Proposition 3.1
Let![]() ,
, ![]() and let:
and let:
![]() , (24)
, (24)
i.e. let ![]() then a solution of problem (20), (21) with the conditions
then a solution of problem (20), (21) with the conditions![]() ,
, ![]() ,
, ![]() , (22), (23) is given by:
, (22), (23) is given by:
![]() , (25)
, (25)
![]() , (26)
, (26)
![]() , (27)
, (27)
where the functions![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , are solution of the following two point boundary value problem:
, are solution of the following two point boundary value problem:
![]() , (28)
, (28)
![]() , (29)
, (29)
![]() , (30)
, (30)
![]() , (31)
, (31)
![]() , (32)
, (32)
![]() , (33)
, (33)
![]() , (34)
, (34)
![]() , (35)
, (35)
![]() , (36)
, (36)
![]() , (37)
, (37)
![]() , (38)
, (38)
![]() , (39)
, (39)
and satisfy condition (47). In fact, as shown later, in order to guarantee that![]() ,
, ![]() ,
, ![]() , defined in (26) is a Gaussian probability density function it is necessary that the functions
, defined in (26) is a Gaussian probability density function it is necessary that the functions![]() ,
, ![]() ,
, ![]() ,
, ![]() , satisfy condition (47). Note that (47) implies
, satisfy condition (47). Note that (47) implies ![]()
![]() Condition (47) is a constraint imposed to the solution of (28)-(39). The equations (28)-(39) are a system of six Riccati ordinary differential equations in six unknowns defined for
Condition (47) is a constraint imposed to the solution of (28)-(39). The equations (28)-(39) are a system of six Riccati ordinary differential equations in six unknowns defined for ![]() equipped with three initial conditions in
equipped with three initial conditions in ![]() and three final conditions in
and three final conditions in![]() .
.
Proof
Let![]() ,
, ![]() ,
, ![]() , where
, where ![]() is given by (25) and
is given by (25) and ![]() is a function to be determined. We have:
is a function to be determined. We have:
![]() , (40)
, (40)
![]() , (41)
, (41)
![]() , (42)
, (42)
![]() . (43)
. (43)
Substituting (40)-(43) in (21) we have:
![]() . (44)
. (44)
In (44) we choose![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() ,
, ![]() ,
, ![]() , where
, where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , are functions to be determined. It is easy to see that with the previous choices from (20) and (44) we have (28)-(39) where
, are functions to be determined. It is easy to see that with the previous choices from (20) and (44) we have (28)-(39) where![]() ,
, ![]() and
and![]() ,
,![]() .
.
Note that when ![]() is given by (26) and
is given by (26) and![]() ,
, ![]() , we have:
, we have:
![]() (45)
(45)
Imposing that![]() ,
, ![]() , from (45) it follows that:
, from (45) it follows that:
![]() , (46)
, (46)
that is:
![]() . (47)
. (47)
Equation (47) implies that![]() ,
, ![]() and guarantees that the function m given by (26) is a Gaussian probability density function in
and guarantees that the function m given by (26) is a Gaussian probability density function in ![]() for
for![]() .
.
Note that a solution of the two point boundary value problem (28)-(39) that satisfies (47) may or may not exist. When it does not exist the attempt of building a solution of problem (20), (21) with the conditions![]() ,
,
![]() ,
, ![]() , (22), (23), based on (25)-(27) fails. Conversely when there exist the formulae (25)-(27) and the solution of the constrained two point boundary value problem discussed above gives an elementary solution
, (22), (23), based on (25)-(27) fails. Conversely when there exist the formulae (25)-(27) and the solution of the constrained two point boundary value problem discussed above gives an elementary solution
of problem (20) (21) with the conditions![]() ,
, ![]() ,
, ![]() , (22), (23) when
, (22), (23) when ![]() is a Gaussian proba-
is a Gaussian proba-
bility density function. Proposition 3.1 shows that when (28)-(39) has a solution that satisfies (47) from the hypothesis ![]() it follows that the probability density function
it follows that the probability density function![]() ,
, ![]() ,
, ![]() , solution
, solution
of problem (20), (21) with the conditions![]() ,
, ![]() ,
, ![]() , (22), (23) can be chosen as the Gaussian probability density function (26) with mean:
, (22), (23) can be chosen as the Gaussian probability density function (26) with mean:
![]() , (48)
, (48)
and variance:
![]() , (49)
, (49)
that is in this case we have:![]() ,
, ![]() , with
, with![]() ,
, ![]() ,
, ![]() , given by (48), (49). In this Section and in Section 4 we assume that the system (28)-(39) has a solution that satisfies (47). In Section 5 we discuss briefly the validity of this assumption and in some test cases we determine a solution of (28)-(39) that
, given by (48), (49). In this Section and in Section 4 we assume that the system (28)-(39) has a solution that satisfies (47). In Section 5 we discuss briefly the validity of this assumption and in some test cases we determine a solution of (28)-(39) that
satisfies (47). In [18] Guéant studies the stationary version of problem (20), (21) with the conditions![]() ,
,
![]() ,
, ![]() (22), (23) and finds a solution given by the functions
(22), (23) and finds a solution given by the functions![]() ,
, ![]() , where
, where![]() ,
, ![]() , is a polynomial of degree two in
, is a polynomial of degree two in ![]() and
and![]() ,
, ![]() , is a Gaussian probability density function.
, is a Gaussian probability density function.
From (25) it follows that:
![]() , (50)
, (50)
where ![]()
![]() is the solution of (1), (2) when
is the solution of (1), (2) when ![]() is given by (50). Therefore when (50) holds we have:
is given by (50). Therefore when (50) holds we have:
![]() , (51)
, (51)
Proposition 3.2
Let![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() ,
, ![]() ,
, ![]() , be the solution of
, be the solution of
problem (20), (21) with the conditions![]() ,
, ![]() ,
, ![]() , (22), (23) determined in Proposition 3.1
, (22), (23) determined in Proposition 3.1
that we assume to exist. We have![]() ,
, ![]() , where:
, where:
![]() (52)
(52)
and
![]() . (53)
. (53)
The functions ![]() and
and ![]() denote, respectively, the hyperbolic sine and the hyperbolic cosine functions of
denote, respectively, the hyperbolic sine and the hyperbolic cosine functions of ![]() and the function
and the function![]() ,
, ![]() , in (53) is the solution of the two point boundary value problems (32), (33), (38), (39).
, in (53) is the solution of the two point boundary value problems (32), (33), (38), (39).
Moreover let![]() ,
, ![]() , be the expected value of the optimal trading execution rate of the retail traders, defined in (51), we have:
, be the expected value of the optimal trading execution rate of the retail traders, defined in (51), we have:
![]() (54)
(54)
Proof
Differentiating (48) with respect to ![]() we have:
we have:
![]() , (55)
, (55)
from (55) it follows that:
![]() . (56)
. (56)
From (55), (56) we have that![]() ,
, ![]() , satisfies the differential equation:
, satisfies the differential equation:
![]() . (57)
. (57)
Equations (35), (39), (55), (56) imply that Equation (57) can be equipped with the following boundary conditions:
![]() , (58)
, (58)
![]() . (59)
. (59)
It is easy to see that the function (52) is the solution of (57)-(59). Finally substituting (52) in (56) we determine![]() ,
, ![]() , as solution of the first order ordinary differential Equation (56) with the final condition
, as solution of the first order ordinary differential Equation (56) with the final condition
![]() that follows from (58), (59). An elementary computation shows that the function (54) is the solution of (56) that satisfies this last final condition.
that follows from (58), (59). An elementary computation shows that the function (54) is the solution of (56) that satisfies this last final condition.
Formula (54) shows that![]() ,
, ![]() , depends from
, depends from ![]() but does not depend from
but does not depend from![]() . Note that when
. Note that when
![]() we have
we have![]() ,
, ![]() , so that from
, so that from ![]() we have:
we have:![]() ,
, ![]() ,
,
moreover from (57)-(59) when ![]() we have:
we have:![]() ,
,![]() . That is when
. That is when![]() ,
, ![]() ,
, ![]() , is constant, and
, is constant, and ![]() is a linear function of
is a linear function of![]() ,
,![]() .
.
4. The Optimal Trading Execution Strategy of the Big Trader
Let us consider the optimal control problems (15), (16), (7)-(9). The value function![]() ,
, ![]() ,
, ![]() ,
,
of problems (15), (16), (7)-(9) is the maximum of the objective function ![]() determined solving the following constrained optimization problem:
determined solving the following constrained optimization problem:
![]() , (60)
, (60)
subject to the constraint (7), (9) and:
![]() . (61)
. (61)
Note that we have:
![]() . (62)
. (62)
The function ![]()
![]()
![]() is the solution of the following Hamilton Jacobi Bellman equation:
is the solution of the following Hamilton Jacobi Bellman equation:
![]() , (63)
, (63)
with the final condition:
![]() (64)
(64)
where ![]() is the Hamiltonian function of problem (15),
is the Hamiltonian function of problem (15),
(16), (7)-(9). Note that the right hand side of (64) is not a real valued function. The final condition (64) must be
interpreted as prescribing the![]() ,
, ![]() A trading rate
A trading rate![]() ,
, ![]() , such that
, such that ![]() that is
that is
a trading rate that does not satisfy (9), is a rate that at time ![]() has not achieved the goal of liquidating in the time interval
has not achieved the goal of liquidating in the time interval ![]() the position of
the position of ![]() asset shares held by the big trader at time
asset shares held by the big trader at time![]() . To this rate the final conditions (64) attributes an infinite cost, or equivalently attributes a revenue equal to minus infinity. In this sense the final condition (64) translates to the value function
. To this rate the final conditions (64) attributes an infinite cost, or equivalently attributes a revenue equal to minus infinity. In this sense the final condition (64) translates to the value function ![]() the condition (9) imposed to the trading execution strategy
the condition (9) imposed to the trading execution strategy ![]()
![]() .
.
Therefore in order to find the optimal trading execution strategy of the big trader we must solve the following Hamilton Jacobi Bellman equation:
![]() , (65)
, (65)
with final condition (64), where![]() ,
, ![]() , is given by (54). In fact from the knowledge of the value function v solution of (65), (64) we can determine the optimal control
, is given by (54). In fact from the knowledge of the value function v solution of (65), (64) we can determine the optimal control![]() ,
, ![]() , solution of(15), (16), (7)-(9),
, solution of(15), (16), (7)-(9),
using the relation:![]() ,
, ![]() , with
, with![]() ,
, ![]() , solution of (7)-(9).
, solution of (7)-(9).
We have:
Proposition 4.1
Let![]() ,
, ![]() , and
, and![]() ,
, ![]() , be given respectively by (52) and (54), the value function solution of problem (65), (64) can be chosen as:
, be given respectively by (52) and (54), the value function solution of problem (65), (64) can be chosen as:
![]() , (66)
, (66)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() , are given by:
, are given by:
![]() , (67)
, (67)
![]() , (68)
, (68)
![]() . (69)
. (69)
This means that the optimal trading execution rate of the big trader is:
![]() , (70)
, (70)
where in (70)![]() ,
, ![]() , is the solution of (7)-(9) when in (7)
, is the solution of (7)-(9) when in (7)![]() ,
, ![]() , is given by (70).
, is given by (70).
Proof
Let![]() ,
, ![]() ,
, ![]() , be given by (66), we impose that
, be given by (66), we impose that![]() ,
, ![]() ,
, ![]() satisfies (65), (64). It follows that the coefficients
satisfies (65), (64). It follows that the coefficients![]() ,
, ![]() ,
, ![]() ,
, ![]() , that define the function
, that define the function ![]() through (66), must satisfy the system of ordinary differential equations and the final conditions that follow:
through (66), must satisfy the system of ordinary differential equations and the final conditions that follow:
![]() , (71)
, (71)
![]() , (72)
, (72)
![]() , (73)
, (73)
![]() , (74)
, (74)
![]() , (75)
, (75)
![]() , (76)
, (76)
where![]() ,
, ![]() , is given by (54). The final conditions contained in (76) must be interpreted as prescribing
, is given by (54). The final conditions contained in (76) must be interpreted as prescribing![]() . It is easy to see that the functions (67)-(69) satisfy (71)-(76).
. It is easy to see that the functions (67)-(69) satisfy (71)-(76).
Moreover the optimal trading execution rate of the big trader is given by:
![]() (77)
(77)
That is we have Equation (70).
Substituting (70) in (7) and imposing (8) we determine the optimal trading execution strategy of the big trader![]() ,
, ![]() , as solution of the following differential equation:
, as solution of the following differential equation:
![]() , (78)
, (78)
with initial condition:
![]() . (79)
. (79)
Note that the fact that![]() ,
, ![]() , satisfies (8) (or equivalently (79)) is an hypothesis (i.e. the initial condition imposed to
, satisfies (8) (or equivalently (79)) is an hypothesis (i.e. the initial condition imposed to![]() ,
,![]() ) while the fact that
) while the fact that![]() ,
, ![]() , satisfies (9) is a consequence of the choice of
, satisfies (9) is a consequence of the choice of ![]() made, that is of the choice
made, that is of the choice![]() ,
, ![]() , given by (70).
, given by (70).
5. Numerical Experiments
We begin the numerical study of the trading execution model presented in the previous Sections discussing the problem of the existence of solutions of the mean field game problem (5), (6), (1)-(4) of the form suggested in Propositions 3.1, 3.2. The existence of this kind of solutions is equivalent to the assumption that the two point boundary value problem (28)-(39) has a solution that satisfies (47). It is easy to see that the existence of a solution of the two point boundary value problem (28)-(39) that satisfies (47) depends from the existence of a solution of the two point boundary value problem (32), (33), (38), (39) such that![]() ,
,![]() . In fact when the two point boundary value problem (32), (33), (38), (39) has a solution
. In fact when the two point boundary value problem (32), (33), (38), (39) has a solution![]() ,
, ![]() ,
, ![]() such that
such that ![]()
![]() from (52), (54) it follows that we can find:
from (52), (54) it follows that we can find:![]() ,
, ![]() , using Equation (48), (49);
, using Equation (48), (49);![]() ,
, ![]() , using Equation (51), (52), (54);
, using Equation (51), (52), (54);
![]()
![]() using Equation (47) and finally
using Equation (47) and finally![]() , using Equations
, using Equations
(28), (29). Conversely when the two point boundary value problem (32), (33), (38), (39) does not have a solution,
such that![]() ,
, ![]() , the solution of (20), (21) with the conditions
, the solution of (20), (21) with the conditions![]() ,
, ![]() ,
, ![]() , (22),
, (22),
(23) constructed in Propositions 3.1, 3.2 does not exist. The study of the existence problem of the solution of the two point boundary value problem (32), (33), (38), (39) from the mathematical point of view is beyond our purposes here. In the numerical experiments presented in this Section we proceed as follows: first of all the two point boundary value problem (32), (33), (38), (39) is solved numerically using the shooting method (see [19] ) and the condition ![]()
![]() is checked. When this is done successfully from the solution of (32), (33), (38), (39) that satisfies
is checked. When this is done successfully from the solution of (32), (33), (38), (39) that satisfies![]() ,
, ![]() , found numerically we determine the solution of (28)-(31), (34)-(37). Let us study the trading execution model developed in Sections 2, 3 and 4. We present four study cases. In these study cases we use a generalized version of the mean field game problem (5), (6), (1)-(4) where the utility function defined in (6) is substituted with a new utility function that depends from some new parameters. Let us explain in detail the choices made. We recall that the utility function defined in (6) is the sum of the following terms:
, found numerically we determine the solution of (28)-(31), (34)-(37). Let us study the trading execution model developed in Sections 2, 3 and 4. We present four study cases. In these study cases we use a generalized version of the mean field game problem (5), (6), (1)-(4) where the utility function defined in (6) is substituted with a new utility function that depends from some new parameters. Let us explain in detail the choices made. We recall that the utility function defined in (6) is the sum of the following terms:
![]() ,
,![]() ,
, ![]() and
and![]()
with![]() ,
, ![]() ,
,![]() . As already explained in Sections 2 and 3 the second and the third term in different ways express the fact that the retail traders are risk adverse. Maximizing (6) the retail traders pursue three goals. The first one is the desire of adopting similar strategies (i.e. the desire of the retail traders of not being alone in the
. As already explained in Sections 2 and 3 the second and the third term in different ways express the fact that the retail traders are risk adverse. Maximizing (6) the retail traders pursue three goals. The first one is the desire of adopting similar strategies (i.e. the desire of the retail traders of not being alone in the
market). This goal is pursued making big the term ![]() of the utility function. The second goal is the desire of avoiding risk. This goal is pursued making big the term
of the utility function. The second goal is the desire of avoiding risk. This goal is pursued making big the term ![]() of the utility function. In this term the risk aversion is declined in two ways: aversion to abrupt changes of trading strategies expressed by the term
of the utility function. In this term the risk aversion is declined in two ways: aversion to abrupt changes of trading strategies expressed by the term ![]() and aversion to hold open positions on the asset shares expressed by the term
and aversion to hold open positions on the asset shares expressed by the term![]() . The third goal is the desire of having a position on the asset shares close to
. The third goal is the desire of having a position on the asset shares close to ![]() in the long run (i.e. is at time
in the long run (i.e. is at time![]() ). This last goal is pursued making big the term
). This last goal is pursued making big the term![]() . Note that to keep the formulae deduced in Sections 3 and 4 as simple as possible in the utility function (6) the four terms
. Note that to keep the formulae deduced in Sections 3 and 4 as simple as possible in the utility function (6) the four terms
![]() ,
,![]() ,
,![]() ,
,![]()
are weighted in a predetermined way. However to show the versatility of the model developed in the previous Sections in the study cases presented in this Section it is convenient to introduce a new utility function containing two parameters not present in (6), that is: the parameter w that regulates the relative weights of the terms
![]() and
and ![]() and the parameter
and the parameter ![]() that regulates the relative weights of the terms
that regulates the relative weights of the terms ![]() and
and![]() . That is in this Section we consider the utility function:
. That is in this Section we consider the utility function:
![]() (80)
(80)
instead of the utility function ![]() defined in (6). Note that in (80) we choose
defined in (6). Note that in (80) we choose![]() ,
, ![]() , and that the parameter
, and that the parameter ![]() of (8) replaces the parameter
of (8) replaces the parameter ![]() of (6). For simplicity in (80) we exclude the choices
of (6). For simplicity in (80) we exclude the choices ![]() and/or
and/or ![]() from the possible choices of the parameter values. In fact when in (80) we have
from the possible choices of the parameter values. In fact when in (80) we have ![]() and/or
and/or ![]() the resulting mean field game problem is degenerate. That is the choices
the resulting mean field game problem is degenerate. That is the choices ![]() and/or
and/or ![]() in (80) correspond to a problem with a non convex Hamiltonian, that is correspond to a degenerate problem. For sim-
in (80) correspond to a problem with a non convex Hamiltonian, that is correspond to a degenerate problem. For sim-
plicity we avoid degenerate problems. Note that![]() ,
, ![]() ,
, ![]() where
where ![]()
is the utility function (6) with ![]() When the utility function (6) is substituted with the utility function (80) and instead of the problem studied in Section 3 we consider the problem of maximizing (80) subject to the constraints (1)-(4) some obvious changes must be made to the statement of Proposition 3.1, to the optimal trading execution rate (50) and to the results derived in Proposition 3.2. However it is easy to see that the analysis of the problem of maximizing (6) subject to the constraints (1)-(4) carried out in Section 3 can be extended to the problem of maximizing (80) subject to the constraints (1)-(4). To keep the exposition simple we leave to the reader the effort of working out these details.
When the utility function (6) is substituted with the utility function (80) and instead of the problem studied in Section 3 we consider the problem of maximizing (80) subject to the constraints (1)-(4) some obvious changes must be made to the statement of Proposition 3.1, to the optimal trading execution rate (50) and to the results derived in Proposition 3.2. However it is easy to see that the analysis of the problem of maximizing (6) subject to the constraints (1)-(4) carried out in Section 3 can be extended to the problem of maximizing (80) subject to the constraints (1)-(4). To keep the exposition simple we leave to the reader the effort of working out these details.
Let us point out that the aversion to abrupt position changes and the possession of stable positions in the asset shares are typical habits of the so called buy and hold investors. Instead the so called short term investors do not like to have stable positions in the asset shares. This last kind of investors open and close their positions within a relatively short time period to exploit short term movements of the asset share price. Based on these facts we argue that the utility function (80) when ![]() is close to one describes buy and hold investors while when
is close to one describes buy and hold investors while when ![]() is close to zero describes short term investors. Moreover it is easy to see that the parameter
is close to zero describes short term investors. Moreover it is easy to see that the parameter ![]() measures the desire of the retail traders of behaving in a similar way. This desire decreases when
measures the desire of the retail traders of behaving in a similar way. This desire decreases when ![]() increases.
increases.
In the study cases that follow we consider the solution of the problem:
![]() , (81)
, (81)
when ![]() is given by (80) subject to the constraints (1)-(4) when
is given by (80) subject to the constraints (1)-(4) when![]() ,
, ![]() ,
, ![]() ,
, ![]() , and we study how the solution of the previous problem influences the trading execution strategy adopted by the big trader to implement the liquidation order.
, and we study how the solution of the previous problem influences the trading execution strategy adopted by the big trader to implement the liquidation order.
In the first study case we analyze the behaviour of the retail traders and we choose![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() ,
,![]() . When
. When![]() ,
, ![]() we consider the optimal trading execution strategy of the retail traders solution of problems (80), (81), (1)-(4) determined with the technique presented in Section 3. The optimal trading execution strategy solution of the previous mean field game problem can be defined through the Gaussian probability density function
we consider the optimal trading execution strategy of the retail traders solution of problems (80), (81), (1)-(4) determined with the technique presented in Section 3. The optimal trading execution strategy solution of the previous mean field game problem can be defined through the Gaussian probability density function![]() ,
, ![]() ,
, ![]() , of the trading position of the retail traders
, of the trading position of the retail traders![]() ,
,![]() . Moreover from the knowledge of
. Moreover from the knowledge of![]() ,
, ![]() ,
, ![]() , we can deduce the expected value of the optimal trading execution rate of the retail traders
, we can deduce the expected value of the optimal trading execution rate of the retail traders![]() ,
, ![]() , given by (54). Using the notation of Section 3 we have:
, given by (54). Using the notation of Section 3 we have:![]() ,
,![]() . Note that
. Note that![]() ,
, ![]() , depends from
, depends from ![]() and
and ![]() while
while ![]() and
and![]() ,
, ![]() , depend from
, depend from ![]() but are independent of
but are independent of![]() . Given the choice of the parameter values stated above Figure 1, Figure 2 show the functions
. Given the choice of the parameter values stated above Figure 1, Figure 2 show the functions![]() ,
, ![]() ,
, ![]() obtained as solution of problem (81), (80), (1)-(4) when
obtained as solution of problem (81), (80), (1)-(4) when![]() ,
, ![]() and
and![]() . In particular Figure 1, Figure 2 show that
. In particular Figure 1, Figure 2 show that![]() ,
, ![]() and,
and, ![]() ,
, ![]() , when
, when ![]() are smaller than when
are smaller than when![]() . This means that the impact of the trading activity of the retail traders on the asset share price when
. This means that the impact of the trading activity of the retail traders on the asset share price when ![]() is smaller than when
is smaller than when![]() . This is coherent with the fact that when
. This is coherent with the fact that when ![]() the retail traders are (mainly) buy and hold investors that hold stable open positions of the asset shares and that retail traders of this kind do not like to change abruptly their trading strategies. Conversely when
the retail traders are (mainly) buy and hold investors that hold stable open positions of the asset shares and that retail traders of this kind do not like to change abruptly their trading strategies. Conversely when ![]() the retail traders are (mainly) short term investors that prefer to open and close their positions in a relatively small time period rather than holding stable open positions of the asset shares. Figure 3, Figure 4 show the function
the retail traders are (mainly) short term investors that prefer to open and close their positions in a relatively small time period rather than holding stable open positions of the asset shares. Figure 3, Figure 4 show the function![]() ,
, ![]() , when
, when![]() ,
, ![]() and
and![]() . In particular Figure 3, Figure 4 show that when
. In particular Figure 3, Figure 4 show that when ![]() increases the variance
increases the variance![]() ,
, ![]() , increases, that is when
, increases, that is when ![]() increases the retail traders adopt more diversified trading positions in the asset shares market. This is coherent with the understanding that increasing
increases the retail traders adopt more diversified trading positions in the asset shares market. This is coherent with the understanding that increasing ![]() decreases the desire of the retail traders of having similar strategies.
decreases the desire of the retail traders of having similar strategies.
In the second, third and fourth study cases we study the behaviour of the big trader during the execution of a liquidation order, that is we consider the solution of the optimal control problem (15), (16), (7)-(9). In particular we study the dependence of the behaviour of the big trader from the behaviour of the retail traders determined solving problem (81), (80), (1)-(4).
In the study cases presented we assume that the number of asset shares held by the big trader at time ![]() is
is ![]() and that the final time within which the sale of the
and that the final time within which the sale of the ![]() asset shares must be completed is
asset shares must be completed is![]() . Recall that the time horizon of the mean field game problem that describes the retail traders is chosen as
. Recall that the time horizon of the mean field game problem that describes the retail traders is chosen as![]() . We choose
. We choose![]() ,
, ![]() in (16). Recall that (16) does not depend from
in (16). Recall that (16) does not depend from![]() .
.
We solve the differential Equation (7) with the initial condition (8). Recall that in (7)![]() ,
, ![]() ,
, ![]() , are determined solving the mean field game problem associated to the retail traders and depend on
, are determined solving the mean field game problem associated to the retail traders and depend on![]() . As consequence the functions
. As consequence the functions ![]() and
and![]() ,
, ![]() determined solving the optimal control problem associated to the big trader depend from
determined solving the optimal control problem associated to the big trader depend from![]() . The solution
. The solution![]() ,
, ![]() of (7) that satisfies (8) is:
of (7) that satisfies (8) is:
![]() , (82)
, (82)
that corresponds to the trading rate:
![]() . (83)
. (83)
Note that when ![]() the function
the function![]() ,
, ![]() , defined in (82) satisfies (9), that is we have
, defined in (82) satisfies (9), that is we have![]() . Moreover when
. Moreover when ![]() that is when the behaviour of the retail traders does not contribute to the asset share price equation, the optimal trading execution strategy of the big trader resulting from (82), (83) is:
that is when the behaviour of the retail traders does not contribute to the asset share price equation, the optimal trading execution strategy of the big trader resulting from (82), (83) is:
![]() ,
,![]() . This strategy corresponds to the sale of the
. This strategy corresponds to the sale of the ![]() asset shares held at time
asset shares held at time ![]()
with constant trading rate![]() ,
, ![]() , during the time interval
, during the time interval![]() . That is the strategy determined using the model developed in the previous Sections when
. That is the strategy determined using the model developed in the previous Sections when ![]() coincides with the optimal trading execution strategy of a risk neutral trader found by Almgren in [2] . It is easy to see that the instantaneous market impact of the trading activity of the retail traders introduced in Equation (10) (i.e. the term
coincides with the optimal trading execution strategy of a risk neutral trader found by Almgren in [2] . It is easy to see that the instantaneous market impact of the trading activity of the retail traders introduced in Equation (10) (i.e. the term![]() ,
, ![]() of (10)) can be seen as a kind of directional view of the big trader about the asset share price dynamics. Note that
of (10)) can be seen as a kind of directional view of the big trader about the asset share price dynamics. Note that
since ![]() Equation (56) implies that
Equation (56) implies that ![]() has the same sign of
has the same sign of![]() ,
,![]() . This means that positive values of
. This means that positive values of ![]() imply that
imply that ![]() is positive, that is the “majority” of the retail traders are “buyers” of the asset shares, vice versa negative values of
is positive, that is the “majority” of the retail traders are “buyers” of the asset shares, vice versa negative values of ![]() imply that
imply that ![]() is negative, that is the “majority” of the retail traders
is negative, that is the “majority” of the retail traders
are “sellers” of the asset shares. Recall that when ![]() the trading activity of the retail traders influences the asset share price dynamics through the term
the trading activity of the retail traders influences the asset share price dynamics through the term ![]() of the asset share price equation and, as a consequence, influences the optimal trading execution strategy of the big trader.
of the asset share price equation and, as a consequence, influences the optimal trading execution strategy of the big trader.
In the second study case we choose![]() ,
, ![]() and
and ![]() in the mean field game model that describes the retail traders and we study the corresponding optimal trading execution strategy of the big trader as
in the mean field game model that describes the retail traders and we study the corresponding optimal trading execution strategy of the big trader as
a function of ![]() and
and![]() ,
,![]() . Recall that when
. Recall that when ![]() we have
we have![]() ,
, ![]() ,
,
therefore when ![]() the solution of the mean field game problem (81), (80), (1)-(4) corresponds to the solution of problems (5), (6), (1)-(4) with
the solution of the mean field game problem (81), (80), (1)-(4) corresponds to the solution of problems (5), (6), (1)-(4) with ![]() Recall that we have chosen
Recall that we have chosen![]() . Figure 5 shows the optimal trading execution strategy of the big trader resulting from the formulae presented in Section 4 for
. Figure 5 shows the optimal trading execution strategy of the big trader resulting from the formulae presented in Section 4 for
several values of![]() . When
. When ![]() and
and ![]() we have
we have![]() ,
,![]() . In this case we obtain as optimal trading execution strategy of the big trader the optimal trading execution strategy of the risk neutral trader found by Almgren in [2] (i.e. selling with constant rate, this is the straight line segment shown in Figure 5). When
. In this case we obtain as optimal trading execution strategy of the big trader the optimal trading execution strategy of the risk neutral trader found by Almgren in [2] (i.e. selling with constant rate, this is the straight line segment shown in Figure 5). When ![]() and
and ![]() we have
we have![]() ,
, ![]() , that is the “majority” of the retail traders have long positions on
, that is the “majority” of the retail traders have long positions on
the asset shares and ![]() that is the “majority” of the retail traders are buyers of the asset shares in the time
that is the “majority” of the retail traders are buyers of the asset shares in the time
interval ![]() and the asset share price tends to increase in the time interval
and the asset share price tends to increase in the time interval![]() . This determines the behaviour of the big trader. In fact in this case the big trader waits to sell his shares at the end of the time interval
. This determines the behaviour of the big trader. In fact in this case the big trader waits to sell his shares at the end of the time interval ![]() assigned to execute the liquidation order, even more the big trader buys asset shares at the beginning of the time interval
assigned to execute the liquidation order, even more the big trader buys asset shares at the beginning of the time interval ![]() assigned to execute the liquidation order (i.e. we have
assigned to execute the liquidation order (i.e. we have ![]() when
when ![]() is close to zero) to take advantage of the expected rise of the asset share price in the time interval
is close to zero) to take advantage of the expected rise of the asset share price in the time interval ![]() induced by the
induced by the
behaviour of the retail traders. That is in this case the trading execution strategy![]() ,
, ![]() , of the big
, of the big
trader is a concave function that connects the points![]() ,
, ![]() of the
of the ![]() plane as shown in Figure 5, Figure 6. When
plane as shown in Figure 5, Figure 6. When ![]() and
and ![]() we have
we have![]() ,
, ![]() , that is the “majority” of the retail traders
, that is the “majority” of the retail traders
have short positions on the asset shares (and ![]() that is the “majority” of the retail traders are sellers of
that is the “majority” of the retail traders are sellers of
the asset shares in the time interval![]() ) and the asset share price tends to decrease in the time interval
) and the asset share price tends to decrease in the time interval![]() . This fact induces the big trader to anticipate the sale of his asset shares at the beginning of the time interval
. This fact induces the big trader to anticipate the sale of his asset shares at the beginning of the time interval ![]() to limit losses due to the expected fall of the asset share price in the time interval
to limit losses due to the expected fall of the asset share price in the time interval ![]() induced by the behaviour of the retail traders. That is in this case the trading execution strategy
induced by the behaviour of the retail traders. That is in this case the trading execution strategy ![]()
![]() is a convex function that connects the points
is a convex function that connects the points![]() ,
, ![]() of the
of the ![]() plane as shown in Fig- ure 5, Figure 7. Note that Figure 5, Figure 7 show that during the liquidation order
plane as shown in Fig- ure 5, Figure 7. Note that Figure 5, Figure 7 show that during the liquidation order![]() ,
, ![]() can be negative. That is the big trader can use short selling to maximize the revenue resulting from the execution of the liquidation order. Moreover Figure 6, Figure 7 show the optimal trading execution strategy of the big trader when the absolute value of
can be negative. That is the big trader can use short selling to maximize the revenue resulting from the execution of the liquidation order. Moreover Figure 6, Figure 7 show the optimal trading execution strategy of the big trader when the absolute value of ![]() increases. Figure 6, Figure 7 show that when the absolute value of
increases. Figure 6, Figure 7 show that when the absolute value of ![]() increases the influence of the behaviour of the retail traders on the asset share price dynamics increases and as a consequence the influence of the behaviour of the retail traders on the optimal trading execution strategy of the big trader increases. That is the optimal trading execution strategy of the big trader becomes respectively more concave (Figure 6) or more convex (Figure 7) whe
increases the influence of the behaviour of the retail traders on the asset share price dynamics increases and as a consequence the influence of the behaviour of the retail traders on the optimal trading execution strategy of the big trader increases. That is the optimal trading execution strategy of the big trader becomes respectively more concave (Figure 6) or more convex (Figure 7) whe ![]() increases and
increases and ![]() or
or ![]() increases and
increases and![]() .
.
In the third study case in the mean field game model that describes the retail traders we assume ![]()
![]() ,
, ![]() and we study the corresponding optimal trading execution strategy of the big trader when
and we study the corresponding optimal trading execution strategy of the big trader when ![]() varies in
varies in![]() . The remaining parameters of the trading execution model have the same values than in the
. The remaining parameters of the trading execution model have the same values than in the
second study case. We recall that when ![]() and
and ![]() we have
we have![]() ,
, ![]() ,
, ![]() , that is in
, that is in
the time interval ![]() the “majority” of retail traders are long on the asset shares and are buyers, the asset share price tends to increase, and the big trader expects rising prices of the asset shares. The value assigned to
the “majority” of retail traders are long on the asset shares and are buyers, the asset share price tends to increase, and the big trader expects rising prices of the asset shares. The value assigned to ![]() distinguishes the retail traders in buy and hold investors (
distinguishes the retail traders in buy and hold investors (![]() close to one) and short term investors (
close to one) and short term investors (![]() close to zero). When
close to zero). When ![]() is close to zero (i.e. the retail traders are short term investors) the short term character of the retail traders amplifies the bullish direction of the market in comparison to the bullish direction of the market induced in the same circumstances by buy and hold retail traders (
is close to zero (i.e. the retail traders are short term investors) the short term character of the retail traders amplifies the bullish direction of the market in comparison to the bullish direction of the market induced in the same circumstances by buy and hold retail traders (![]() close to one). As a consequence in presence of short term retail traders the big trader enhances the choice of moving the sale of the asset shares at the end of the time interval
close to one). As a consequence in presence of short term retail traders the big trader enhances the choice of moving the sale of the asset shares at the end of the time interval![]() . On the other hand when
. On the other hand when ![]() is close to one (i.e. the retails traders are buy and hold investors) the buy and hold character of the retail traders reduces the rise of the asset share price induced by the retail traders in comparison to the rise induced by the short term retail traders in similar circumstances. As a consequence in presence of buy and hold retail traders the big trader mitigates the choice of moving the sale of the asset shares at the end of the time interval
is close to one (i.e. the retails traders are buy and hold investors) the buy and hold character of the retail traders reduces the rise of the asset share price induced by the retail traders in comparison to the rise induced by the short term retail traders in similar circumstances. As a consequence in presence of buy and hold retail traders the big trader mitigates the choice of moving the sale of the asset shares at the end of the time interval![]() . That is leaving unchanged the other parameters of the numerical experiment (i.e.
. That is leaving unchanged the other parameters of the numerical experiment (i.e.![]() ,
,![]() ) the trading execution strategy of the big trader should be less concave in presence of retail traders that are buy and hold investors than in presence of retail traders that are short term investors. A similar analysis can be carried out to deduce the behaviour of the big trader suggested by the model when
) the trading execution strategy of the big trader should be less concave in presence of retail traders that are buy and hold investors than in presence of retail traders that are short term investors. A similar analysis can be carried out to deduce the behaviour of the big trader suggested by the model when ![]() and
and![]() . Figure 8 shows the optimal trading execution strategy of the big trader when
. Figure 8 shows the optimal trading execution strategy of the big trader when![]() ,
, ![]() ,
, ![]() and
and![]() . Figure 9 shows the optimal trading execution strategy of the big trader when
. Figure 9 shows the optimal trading execution strategy of the big trader when![]() ,
, ![]() ,
, ![]() and
and![]() . Figure 8, Figure 9 confirm quantitatively the previous qualitative analysis.
. Figure 8, Figure 9 confirm quantitatively the previous qualitative analysis.
In the fourth study case we assume ![]() and
and ![]() in the mean field game model that describes the retail traders and we study the corresponding optimal trading execution strategy of the big trader as a function of
in the mean field game model that describes the retail traders and we study the corresponding optimal trading execution strategy of the big trader as a function of![]() ,
, ![]() and
and![]() ,
,![]() . Figure 10 shows the function
. Figure 10 shows the function![]() ,
, ![]() obtained as solution of problem (81),
obtained as solution of problem (81),
(80), (1)-(4) when![]() ,
, ![]() ,
, ![]() and
and![]() . We observe that when
. We observe that when ![]() and
and ![]() the
the
function![]() ,
, ![]() changes sign in the time interval
changes sign in the time interval ![]() in fact the function
in fact the function![]() ,
, ![]() from being positive in a neighborhood of
from being positive in a neighborhood of ![]() becomes negative in a neighborhood of
becomes negative in a neighborhood of![]() . Recall that Equation (56)
. Recall that Equation (56)
implies that when ![]() changes sign also
changes sign also ![]() changes sign. That is in the time interval
changes sign. That is in the time interval ![]() the “majority”
the “majority”
of the retail traders from being buyers of the asset shares when ![]() is close to zero become sellers of the asset shares when
is close to zero become sellers of the asset shares when ![]() is close to
is close to![]() .
.
Figure 11 shows the optimal trading execution strategy of the big trader corresponding to the behaviour of the retail traders shown in Figure 10. Figure 11 shows that the big trader as a consequence of the behaviour of the retail traders initially waits to sell his shares, this is coherent with the fact that at the beginning the retail traders are buyers. However later, when the retail traders become sellers and the asset share price tends to decrease, Figure 11 shows that the big trader changes strategy and tries to anticipate the sale at the beginning of the time
interval that remains to conclude the execution of the liquidation order. That is the optimal trading execution strategy of the big trader![]() ,
, ![]() , shown in Figure 11, from being a concave function of
, shown in Figure 11, from being a concave function of ![]() when
when ![]() is close to zero becomes a convex function of
is close to zero becomes a convex function of ![]() when
when ![]() is close to
is close to ![]() and the saddle point of
and the saddle point of![]() ,
, ![]() , is the value of
, is the value of ![]() that corresponds to the zero of the function
that corresponds to the zero of the function![]() ,
,![]() . Finally Figure 12 shows the function
. Finally Figure 12 shows the function![]() ,
, ![]() , obtained as solution of problems (81), (80), (1)-(4) when
, obtained as solution of problems (81), (80), (1)-(4) when![]() ,
, ![]() ,
, ![]() and
and![]() . We observe that when
. We observe that when ![]() and
and ![]() the function
the function![]() ,
, ![]() , changes sign in the time interval
, changes sign in the time interval![]() , in fact the function
, in fact the function![]() ,
, ![]() from being negative in a neighborhood of
from being negative in a neighborhood of ![]() becomes positive in a neighborhood of
becomes positive in a neighborhood of![]() . That is in the time interval
. That is in the time interval ![]() the “majority” of the retail traders from being sellers of the asset shares when
the “majority” of the retail traders from being sellers of the asset shares when ![]() is close to zero become buyers of the asset shares
is close to zero become buyers of the asset shares
when ![]() is close to
is close to ![]() Figure 13 shows the optimal trading execution strategy of the big trader corresponding to the behaviour of the retail traders shown in Figure 12. Figure 13 shows that the big trader as a consequence of the behaviour of the retail traders when
Figure 13 shows the optimal trading execution strategy of the big trader corresponding to the behaviour of the retail traders shown in Figure 12. Figure 13 shows that the big trader as a consequence of the behaviour of the retail traders when ![]() is close to zero anticipates the sale of his shares coherently with the fact that the retail traders are sellers. Later when
is close to zero anticipates the sale of his shares coherently with the fact that the retail traders are sellers. Later when ![]() is close to
is close to![]() , Figure 13 shows that the retail traders become buyers and the asset share price tends to increase, as a consequence the big trader waits to sell his asset shares at the end of the time interval that remains to conclude the execution of the liquidation order. That is Figure 13 shows that the optimal trading execution strategy of the big trader
, Figure 13 shows that the retail traders become buyers and the asset share price tends to increase, as a consequence the big trader waits to sell his asset shares at the end of the time interval that remains to conclude the execution of the liquidation order. That is Figure 13 shows that the optimal trading execution strategy of the big trader![]() ,
, ![]() , from being a convex function of
, from being a convex function of ![]() when
when ![]() is close to zero becomes a concave function of
is close to zero becomes a concave function of ![]() when
when ![]() is close to
is close to ![]() and that the saddle point of
and that the saddle point of![]() ,
, ![]() , is located at the value of
, is located at the value of ![]() that corresponds to the zero of the function
that corresponds to the zero of the function![]() ,
,![]() .
.
The interested reader is referred to the website: http://www.econ.univpm.it/recchioni/finance/w19 to find material including animations, an interactive application and an app that helps the understanding of this paper. A general reference to the work of the authors and of their coauthors in mathematical finance is the website: http://www.econ.univpm.it/recchioni/finance.