1. Introduction
Textbooks of fluid dynamics that mention the capillary wave (or ripples) generally have much less to say about them than they do about the surface gravity wave [1] -[4] . Is this because of their smaller wavelengths and amplitudes? Fundamental properties are not even touched upon, such as the linear and angular momentum of the waves. Presumably, but not stated in the cited references, the fluid particles have an orbital motion, when viewed in the fixed frame, which decays with increasing depth down from the equilibrium free surface. If so, both linear and angular momentum will be propagated with the wave in addition to the better known transport of energy common to all types of waves. Some familiarity with the linear momentum of surface gravity waves comes from its relation to the Stokes drift. From the orbital motion of the fluid particles in propagating waves it is obvious that they possess (orbital) angular momentum.
How the capillary wave motion decays with depth is pretty much taken to be exponential in the classical studies. This is a consequence of assuming irrotational motion with a velocity potential, because when the horizontal motion is selected to be harmonic, i.e. wave like, then the vertical motion must be exponential in order to satisfy Laplace’s equation for the velocity potential. Physical understanding of the depth decay feature is thereby avoided by this mathematical procedure.
An alternative decay law is proposed below, which in all likelihood will not turn out to be exponential in character. There are advantages and disadvantages to the new approach to describing the capillary wave. A definite advantage is that the governing differential equations for the pressure and velocity, that result from combining two elementary pieces of physics, are linear. Another advantage is that there is no necessity to adopt irrotationality ab initio. One disadvantage of the operating equations is that they contain a non-constant coefficient which prevents complete solutions from being obtained at the present time without further theoretical or observational information being supplied to these equations. The non-constant coefficient is the radius of curvature of the streamlines. Measurements will eventually show that the radius of curvature increases with increasing depth from a minimum at the surface to infinity at a depth comparable to a wavelength, and perhaps the exact rate of decay will be uncovered also.
First principle of physics adopted here is the usual law of Bernoulli, where the speed is the greatest, the pressure is the least, applied along streamlines in the steady frame, but with the addition of a novelty: a term involving surface tension of the air/water interface. The second piece is the force balance on fluid particles traveling along curved paths. In the cross-stream direction the centrifugal force is balanced by a pressure gradient. Use of the centrifugal force is not novel but it is still controversial within classical physics.
2. Method
In the steady reference frame the wave shape is motionless to the observer and the fluid flows steadily past him under the wave. Applying Bernoulli’s law to the streamline at the air/water interface of the capillary wave yields
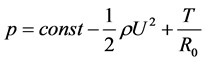 (1)
(1)
where p is the pressure and U is the fluid speed parallel to the streamline. Constants of the motion on the RHS (right hand side) are  (taken the same for all streamlines), the density
(taken the same for all streamlines), the density 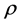 and the surface tension T. The radius of curvature at the surface
and the surface tension T. The radius of curvature at the surface 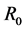 is computed in the plane of the mean flow.
is computed in the plane of the mean flow.
On the RHS of (1) the third term is not normal. It replaces the usual gravity term, but for capillary waves gravity’s influence is assumed to be small compared to that of surface tension. In fact, I have not seen Bernoulli’s law displayed anywhere in a text describing capillary waves.
Recently a form of Bernoulli’s equation similar to (1) was used to give a qualitative explanation of the vena contracta, only there the radius of curvature in the surface tension term is evaluated in the plane perpendicular to the mean flow direction [5] .
Consider the vertical distance z to be marked positive upward from the top of a crest where it is zero. Then the balance of forces on a horizontally moving fluid particle at any depth below the crest is
 (2)
(2)
where U, R and p are functions of z. On the LHS (left hand side) of (2) is the pressure force acting down; the centrifugal force acting up is on the RHS. There are now two equations in the two unknowns, 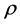 ,
, 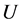 , and as they stand each of the two equations is nonlinear.
, and as they stand each of the two equations is nonlinear.
Details of the method will be kept brief because they are similar to those recently produced for the surface gravity wave [6] . Eliminate the velocity between Equations (1) and (2), remembering that below the surface the surface tension term in (1) vanishes since there is no surface tension underneath the air/water interface. The result is a pressure equation
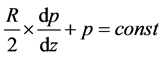 (3)
(3)
This differential equation is linear, ordinary and of the first order. The non-constant coefficient is R. Solution of (3) begins with the homogeneous part of the equation: the RHS set to zero, followed by separation of variables.
 (4)
(4)
Both sides of (4) can immediately be integrated to give
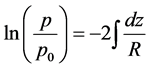 (5)
(5)
where  is a constant. Then both sides of (5) can be raised to the power of e to get
is a constant. Then both sides of (5) can be raised to the power of e to get
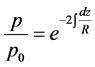 (6)
(6)
Plus an additive constant on the RHS (not displayed). As (6) shows, the depth decay rate for pressure variations is given by the exponent of the exponential on the RHS.
Now, the factor of 2 in the exponent of the RHS of (6) is very significant, as can be made clear. If instead of eliminating the velocity between (1) and (2) to get a pressure equation, the pressure can be eliminated between the same two equations to get the velocity equation by first differentiating (1) with respect to z. What will be found is an equation similar to (3) with U replacing p and with the factor of 2 missing. Then the solution is similar to (6) with U replacing p and the factor of 2 again missing. Since the depth decay rate for velocity variations equals the exponent in the exponential, which is a factor of 2 smaller than that in (6), this proves that, no matter what  is, pressure variations die away with increasing depth at a faster rate than do the velocity variations. Exactly the same conclusion was found for the surface gravity wave.
is, pressure variations die away with increasing depth at a faster rate than do the velocity variations. Exactly the same conclusion was found for the surface gravity wave.
Recall the classical result for the surface gravity wave: both pressure and velocity perturbations decrease exponentially with increasing depth down from the equilibrium surface and at the same (e-folding) rate. Even though the radius of curvature function 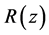 is not exactly known at this point, it is very doubtful that the depth decay rates of the capillary and surface gravity waves will turn out to be the normal exponential one, just from looking at form of Equation (6).
is not exactly known at this point, it is very doubtful that the depth decay rates of the capillary and surface gravity waves will turn out to be the normal exponential one, just from looking at form of Equation (6).
3. Discussion
Finding that the depth rates of decay for pressure and velocity perturbations are significantly different from each other for the capillary wave may come as a surprise to some readers. However, an example of such disparity in steady fluid flow has been available for a few hundred years. Consider a metal cylinder containing water and oriented vertically with gravity acting down. The cylinder has been at constant rotation about its long axis for enough time to establish solid body rotation of the fluid inside it. The horizontal velocity of the flow in the fixed frame of reference is the same as that of the container where they touch and it decreases linearly to zero at the cylinder’s center. On the other hand, the air/water interface has a parabolic shape which implies that the water pressure decreases quadratically radially from the rim to the center.
Although not knowing the details of the radius of curvature function for the streamlines may seem bothersome, once it is found, the governing linear equations can be solved immediately, if not analytically then numerically. Also the solutions for pressure and velocity are not sensitive to the exact path, the radius of curvature takes between its minimum values at the surface to infinity at depth because of the integrations involving the curvature on the RHS.