Unified Field Theory in a Nutshell—Elicit Dreams of a Final Theory Series ()
“We choose to go to the Moon in this decade and do the other things, not because they are easy, but because they are hard.”
―H. E. President John F. Kennedy (1917-1963)
1. Introduction
Much effort by a great many erudite, notable and foremost physicists and mathematicians has gone into the all- noble and all-esoteric search for an all-encompassing unified theory of all the forces of Nature; as for our own attempts, the present reading marks the third such effort. The beguiling problem of how to unify Quantum Theory (QT) and Professor Albert Einstein’s General Theory of Relativity (GTR) into a consistent and coherent unified theoretical framework has not only baffled but eluded the foremost physicists and mathematicians of the past eight decades or so [e.g. Professor―Albert Einstein (1879-1955), Hermann Weyl (1885-1955), Theodor Kaluza (1885-1954), Erwin Schrödinger (1887-1961), Edward Witten (1951-), Stephen Hawking (1942-), etc.; to mention but a few pre-eminent figures in this all-great endeavour], and with the failure in recent times to deliver on its now long overdue promise i.e., failure by the so-called most promising theories on this front (e.g. String and String Related Theories), the need for a unified theory of all the forces of Nature has become particularly urgent and pressing, especially given the most recent announcement of a Higgs-like particle at CERN coincidentally on the occasion of the United States of America’s 236th independence from colonial Britain on the 4th of July 2012. Surely, a universally acceptable form of order is urgently needed in the “House of Physics”.
One of the first major problems beguiling the efforts to finding a unified theory is that each of the two theories in question (i.e. QT and the GTR) is considered by a great many physicists as fundamental physical theories of physics in their own right. By “fundamental physical theory” it is understood that these theories are not derivable from any other physical theory, they are―in Professor Einstein’s terminology, Theories of Principle1. Accepting these theories as fundamental physical theories lands us in torrid philosophical and logical conundrums as this invariably implies the existence of two independent physical realities―one reality of the very small (QT) and the other of the large (GTR), each governed by separate Physical Laws. The strong and existing feeling that there can only be one and only one reality that points to one and only one fundamental physical theory, hence, a unified theory of all of reality is thus needed. Surely, the garment of physical and natural reality must constitute an undivided whole and it thus obviously makes no sense to have two distinct fundamental theories for a single united garment of reality.
Thus far, the attainment of a unified field theory has proved to be elusive, it is thus reasonable to ask “How does it come about that physicists have for so long been able to succeed in failing to find a unified theory?” Amongst others, we feel―as Dr. Philp Gibbs2, that physicists have held far-too-sacrosanct these two giant pillars of modern physics―i.e., QT and the GTR; and they have in the process, gone so far as to confidently believe that naturally, a logical fusion of the two ideas must lead to paths that lead straight to the depths of an acceptable theory that must take humankind to his next level of understanding of physical and natural reality as we experience it. In his own words about this line of thinking, Dr. Philip Gibbs had this to say [2] :
“String theory has had many opportunities to reveal itself as a ‘bridge to nowhere’ but at each turn the road carries on instead and another bridge is crossed. The theory is very tightly constrained by the need to be consistent with General Relativity and Quantum Mechanics. The theorists are not making it up. They are [only] following the course that logical consistency dictates and it is remarkable that there is anything at all that can match the requirements, but of course there has to be because the Universe exists with these features.”
What the above words remind us are the wise words by the great British-German physicist, Professor Max Born (1882-1970). He once said:
“Science is not [mere] formal logic. It needs the free play of the mind in as great a degree as any other creative art. It is true that this is a gift which can hardly be taught, but its growth can be encouraged in those who already posses it.”
Simple stated, like Dr. Gibbs has correctly said it: the present day theorists are trying to construct a new theory by believing (wrongly or rightly so3) that a theory logically derived from the general theory of relativity and quantum mechanics will naturally lead to a logically correct theory which unifies both theories. For example, one of the co-founders of string theory―the pre-eminent Japanese-American physicist, Professor Miko Kaku, in one of his popular television shows, he frankly admits that the traditional way of doing science [i.e., of observation a hypothesis a theorisation a prediction a falsification] is thrown out the window when it comes to string theory; in this field, one has to relay on intelligent guess work as they march forward in their arduous search for a theory that is logically consistent with what already exists and is accepted by the majority of scientist as a theory representative of the present Universe.
The folly (perhaps) in this approach or way of reasoning is that we are forgetting the wise words of the great Professor Max Born that “science is not [mere] formal logic it needs the free play of the mind in as great a degree as any other creative art”. Logic alone is not enough, nor is intuition, we need all these “forces” at play together with a modicum but strong dose of imagination which Professor Einstein said “is more important than knowledge”. We need a leap out of logic to make it into the next virgin territory. Perhaps we must remind the reader of other wise words by one of Germany’s greatest scientists, Professor Karl Ernst Ludwig Marx Planck (1858-1947), who in his lifetime once said that:
“The man who cannot occasionally imagine events and conditions of existence that are contrary to the causal principle as he knows it will never enrich his science by the addition of a new idea.”
Because it has happened and we have experienced it, everyone will concur that no amount of applied research on the candle (or the wax the making it thereof) would have produced the light bulb―to attain the light bulb, the human mind had to leap-out of its ordinary state of conscientiousness. The above words imply that for us to take a leap out of logic and into virgin territory will―at the very least―this requires of us to “imagine events and conditions of existence that are contrary to the causal principle” as we have come to know and experience it. This means that logic may very well not lead to a theory with a direct correspondence with experience. For example, no amount of logical reasoning in Newtonian gravitation would have led mankind into Professor Einstein’s brilliant geometric description of gravitation and spacetime, one had to “defy” logic and enter into much higher planes, terrains and farrows of logic and natural reality.
In this reading―given its length, we find no space to give a wide literature review or an overview of the history of unified field theories. For this, we direct our reader to the excellent review by Emeritus Professor of Physics at Germany’s Göttingen University, Hubert F. M. Goenner; in the readings [3] [4] , he certainly has done a splendid job on that, he has given an extensively review of the history of unified theories from 1918 to 1865. Therefore, we shall proceed as planned without giving a historic overview; we shall give a brief synopsis of the present reading.
In § (2), we outline two fundamental reasons that call for a revision of Professor Einstein’s GTR. In § (3), we give an overview of the reading [5] , and Professor Weyl’s [6] supposedly failed theory is brought back to life. In § (4), we demonstrate an important part of the unified theory to be developed, namely that the metric tensor is in-principle decomposable into a mathematical entity that has not ten free parameters, but four. In § (5), the spacetime upon with the present theory is build is laid down. In § (6), tensorial affinites are proposed in which even the desired spacetime is defined. Once the desired spacetime is defined, in § (7), the general field equations are written down and in § (8), it is shown that as a result of the tensorial nature of the affinities, it is possible to get rid of the non-linear terms of the resulting curvature tensor, thereby making the theory a linear theory. From this linear spacetime with tensorial affinities, in § (9), we write down the resulting field equation. Having laid down the theory, in § (10), we take stock of what has been achieved thus far. In § (11), we show how one can bring the gravitational force into the fold of the proposed unified theory. In § (12) we write down an appropriate geodesic equation that employs tensorial affinities. In § (13), we demonstrate that the proposed unified theory does contain Yang-Mills Theory and finally in § (14), (15) and (16), we give a general discussion, the conclusion drawn thereof and the recommendations for future works.
2. Motivation
Other than the shear and insatiable human desire to be part of such a noble endeavour to finding an all encompassing unified theory of the forces of Nature; if any, what are the real and tangible reasons requiring us to revise Professor Einstein’s GTR? As to ourselves―and as may be the case with the majority of physicists; we find two compelling reasons. The first has to do with the clearly implied need for the unity of the GTR and QM in the simultaneous case of extremely massive and extremely small objects. The second has to do with a well known and largely ignored internal inconsistency of the GTR.
On the first note, QM describes matter at the smallest scale-length as exhibiting both point-particle and wave- like properties. The GTR describes at the largest scale-length the same matter as mere point-particles. There is no wave-like description of matter in the GTR, none whatsoever. However, after exhausting their nuclear fuel which is believed to hold them against the inward tyranny of the gravitational force, massive luminous objects such as stars―whose macroscopic properties are described very well by the GTR; these objects can undergo collapse in which case their spatial size can go down to scale-lengths that require us to use QM to describe them. Under such conditions, it becomes inescapable that one would need a Quantum Theory of Gravity (QTG) in-order to describe the physics in-and-around such objects. For this reason, the need for a QTG is not only clearly evident, but is a dire need and necessity.
On the second note―in our view, one of the major problems that the GTR faces within its own internal structure of logic is that it is based on pure Riemann geometry i.e. a geometry that is well known to violate the Principle of Equivalence at the affine level because the affine connections are not tensors. If pure Riemannian geometry is to be the true geometry to describe the natural World, then, no Laws of Physics should exist at the affine level of Riemann geometry. However, this is not so, since the Geodesic Law:
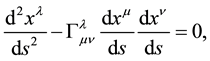 (1)
(1)
that describes the path and motion of particles in spacetime emerges at the affine level. Thus accepting Riemann geometry as a true geometry of Nature means we must accept contrary to the Principle of Relativity that there exists in Nature preferred reference and coordinate systems because the above Geodesic Law leads us to formulating the equations of motion in preferred reference and coordinate systems, namely, geodesic coordinate systems also know as Gaussian coordinate systems.
Einstein’s GTR is based on two Equations (1): the geodesic Equation (1) which determines how particles on in the curved spacetime and (2): the field equation which tells us how matter curves spacetime, i.e.:
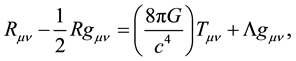 (2)
(2)
where 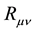 is the contracted Riemann curvature tensor and
is the contracted Riemann curvature tensor and 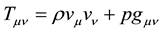 is the stress and energy tensor where
is the stress and energy tensor where 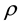 is the density of matter, p is the pressure and
is the density of matter, p is the pressure and  the four velocity, G is Newton’s universal constant of gravitation, c the speed of light and
the four velocity, G is Newton’s universal constant of gravitation, c the speed of light and 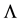 is the controversial and so-called cosmological constant term ad hoc-ly added by Einstein so as to stop the Universe from expanding [7] . Einstein was motivated to include the cosmological constant because of the strong influence from the astronomical wisdom of his day that the Universe appeared to be static and thus was assumed to be so. Besides this, the cosmological constant fulfilled Mach’s Principle [8] , a principle that had inspired Einstein to search for the GTR and he thus thought that the GTR will have this naturally embedded in it―to his dissatisfaction, the GTR did not exactly fullfil this in the manner Einstein had envisaged. Mach’s principle forbids the existence of a truly empty space and at the sametime supposes that the inertia of an object is due to the induction effect(s) of the totality of all-matter in the Universe. Because the field Equation (2) is a tensor, it does not suffer the same problem suffered by the geodesic Equation (1). Unlike (1), the field Equation (2) needs not be formulated exclusively in Gaussian coordinate systems.
is the controversial and so-called cosmological constant term ad hoc-ly added by Einstein so as to stop the Universe from expanding [7] . Einstein was motivated to include the cosmological constant because of the strong influence from the astronomical wisdom of his day that the Universe appeared to be static and thus was assumed to be so. Besides this, the cosmological constant fulfilled Mach’s Principle [8] , a principle that had inspired Einstein to search for the GTR and he thus thought that the GTR will have this naturally embedded in it―to his dissatisfaction, the GTR did not exactly fullfil this in the manner Einstein had envisaged. Mach’s principle forbids the existence of a truly empty space and at the sametime supposes that the inertia of an object is due to the induction effect(s) of the totality of all-matter in the Universe. Because the field Equation (2) is a tensor, it does not suffer the same problem suffered by the geodesic Equation (1). Unlike (1), the field Equation (2) needs not be formulated exclusively in Gaussian coordinate systems.
Gaussian coordinate systems are those coordinate systems such that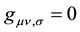 . It can be shown for example that given a flat space-time in which say the rectangular coordinate system (where
. It can be shown for example that given a flat space-time in which say the rectangular coordinate system (where 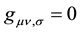 holds) are used to begin with; where [in the rectangular coordinate system] the affinities vanish identically in this system and changing the coordinate system to spherical, the affinities do not vanish. This is a serious desideratum, akin to the Newton-Maxwell conundrum prior to Professor Einstein’s STR i.e., a conundrum of how to reconcile or comprehend the apparent contradiction of the prediction of Professor Maxwell’s theory that demanded that the speed of light be a universal and absolute speed and the Galilean philosophy of relativity that there is no such thing as a universal and absolute speed in the Universe.
holds) are used to begin with; where [in the rectangular coordinate system] the affinities vanish identically in this system and changing the coordinate system to spherical, the affinities do not vanish. This is a serious desideratum, akin to the Newton-Maxwell conundrum prior to Professor Einstein’s STR i.e., a conundrum of how to reconcile or comprehend the apparent contradiction of the prediction of Professor Maxwell’s theory that demanded that the speed of light be a universal and absolute speed and the Galilean philosophy of relativity that there is no such thing as a universal and absolute speed in the Universe.
Given for example, that the affinities represent forces as is the case in the GTR, this means a particle could be made to pass from existence into non-existence (or vis-versa) by simply changing the coordinate system. This on its own violates the Laws of Logic and the need for Nature to preserve Her independent reality devoid of magic. Clearly, the only way out of this conundrum is to seek, as Professors Einstein, Schrödinger etc have done; a theory in which the affinities have a tensor form, hence in the present approach, the first and most important guide is to seek tensorial affinities. Professor Einstein, Schrödinger etc. have made attempts along these lines only to fail. The reason for their failure may perhaps stem from the fact that theirs was a pure mathematical exercise to try to find a set of tensorial affinities from within the framework of the classical spacetime of Riemannian geometry. It should be said that their failure [Professor Einstein, Schrödinger etc.] has not been a total failure as their (failed) work led to significant advances and better insights into the nature of the problem at hand. In-fact, the present work does spring from these so-called failed attempts. Our line of thought stems directly from their line of thought. Thus, we can never say their [Professor Einstein, Schrödinger etc.] effort was in vein.
3. New Weyl Geometry
As already stated, the present UFT is built on a modified theory of Professor Weyl [6] ’s supposedly failed theory of 1918. This modification is presented in [5] . In the present section, we merely give a succinct summary of this work [5] . Therein [5] , we rail against the common approach to finding a unified theory; we revisit the now forgotten “litter” in the dustbins of physics and mathematics history where we make the modest endeavour to resuscitate Professor Hermann Weyl [6] [9] [10] ’s supposedly failed attempted at a unified theory of gravitation and electromagnetism.
In his attempt at a unified theory, Professor Weyl realised that if he supplemented the Christophel three symbols of Riemann geometry i.e.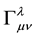 , with a tensorial affine
, with a tensorial affine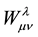 , he obtained a theory with a four vector field
, he obtained a theory with a four vector field 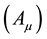 with the desired gauge transformational properties of the electromagnetic four vector field. The Weyl tensorial connection
with the desired gauge transformational properties of the electromagnetic four vector field. The Weyl tensorial connection  is given by:
is given by:
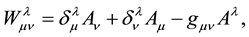 (3)
(3)
where 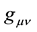 is the metric tensor and
is the metric tensor and 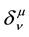 is the Kronecker-Delta function. The resultant affine connection,
is the Kronecker-Delta function. The resultant affine connection, ![]() , of Weyl’s geometry is the sum of the Christophel three symbol
, of Weyl’s geometry is the sum of the Christophel three symbol ![]() and the Weyl tensorial affine
and the Weyl tensorial affine![]() , i.e.
, i.e.![]() . The transformational properties of
. The transformational properties of ![]() and
and ![]() are the same, thus insofar as this aspect of the affines are concerned, the two are equivalent. The affine connection
are the same, thus insofar as this aspect of the affines are concerned, the two are equivalent. The affine connection ![]() is splendidly invariant under the following gauge transformations:
is splendidly invariant under the following gauge transformations:
![]() (4)
(4)
where ![]() is some arbitrary well behaved, smooth, continuous and differentiable function. Given that Professor Weyl knew very well that Maxwellian Electrodynamics is described by a four vector such that the entire Maxwellian Electrodynamics is invariant under the transformation (4b), without wasting much time, the great Professor Weyl seized the golden moment and identified
is some arbitrary well behaved, smooth, continuous and differentiable function. Given that Professor Weyl knew very well that Maxwellian Electrodynamics is described by a four vector such that the entire Maxwellian Electrodynamics is invariant under the transformation (4b), without wasting much time, the great Professor Weyl seized the golden moment and identified ![]() with the Maxwellian four vector potential of Electrodynamics. In his unified theory, Professor Weyl’s quest was based on the subtle idea to treat directions in spacetime on an equal footing with length [11] , that is to say, if the angle of the unit vector changed from one point to the other under parallel transport, why should the length not change too? asked Professor Weyl. Ultimately, this subtle idea bought in electromagnetism into the same fold as gravitation.
with the Maxwellian four vector potential of Electrodynamics. In his unified theory, Professor Weyl’s quest was based on the subtle idea to treat directions in spacetime on an equal footing with length [11] , that is to say, if the angle of the unit vector changed from one point to the other under parallel transport, why should the length not change too? asked Professor Weyl. Ultimately, this subtle idea bought in electromagnetism into the same fold as gravitation.
Professor Weyl’s proposed theory led to a rescaling of the fundamental metric tensor via the gauge transformation,![]() . Professor Weyl held that, this rescaling should have no effect on physics―he was wrong. Professor Einstein initially loved the idea―alas, the devil was in the detail; he noted that the line element
. Professor Weyl held that, this rescaling should have no effect on physics―he was wrong. Professor Einstein initially loved the idea―alas, the devil was in the detail; he noted that the line element ![]() would also be rescaled according to
would also be rescaled according to![]() . Since ds can be made to serve as a measuring rod or clock, the agile Professor Einstein was quick to note that this would mean that certain absolute quantities, such as the spacing of atomic spectral lines and the Compton wavelength of an Electron for example, would change arbitrarily and thus have to depend on their prehistory. With this, Professor Einstein delivered the lethal and venomous blow to Professor Weyl’s theory and concluded that it must therefore be non-physical― despite its grandeur and beauty, it had no correspondence nor bearing with physical and natural reality as we have come to experience.
. Since ds can be made to serve as a measuring rod or clock, the agile Professor Einstein was quick to note that this would mean that certain absolute quantities, such as the spacing of atomic spectral lines and the Compton wavelength of an Electron for example, would change arbitrarily and thus have to depend on their prehistory. With this, Professor Einstein delivered the lethal and venomous blow to Professor Weyl’s theory and concluded that it must therefore be non-physical― despite its grandeur and beauty, it had no correspondence nor bearing with physical and natural reality as we have come to experience.
As aforestated―in the reading [5] ; we put forward a New Weyl Geometry (NWG)―a geometry upon which the present theory is founded. This NWG changes the foundation stone of the Weyl geometry. The metric of the original Weyl geometry is only conformal at the instance of a gauge transformation―i.e., the term ![]() multiplies the metric only when performing a gauge transformation. In the NWG [5] , the metric is intrinsically and inherently conformal. That is to say, if we let
multiplies the metric only when performing a gauge transformation. In the NWG [5] , the metric is intrinsically and inherently conformal. That is to say, if we let ![]() be the metric of the NWG, then,
be the metric of the NWG, then, ![]() where
where ![]() is the conformal term. In the NWG, the conformal term now plays a decisive role in that it is responsible for the attainment of tensorial affinities. This NWG is completely free of Professor Einstein’s lethal and venomous criticism.
is the conformal term. In the NWG, the conformal term now plays a decisive role in that it is responsible for the attainment of tensorial affinities. This NWG is completely free of Professor Einstein’s lethal and venomous criticism.
The NWG is exactly the same geometry is one two all-important differences. The first of which is that the we replace the metric of Riemann geometry ![]() with
with![]() ; the metric is now intrinsically and inherently conformal. The second is that this NWG employs tensorial affinities and this brings about a fundamental difference in that one obtains from this a geometric which is such that vectors now maintain not only their length but their angle as-well upon parallel transport. In § (6), we will provide the details of how in the NWG one obtains tensorial affinities from the conformal terms of the metric
; the metric is now intrinsically and inherently conformal. The second is that this NWG employs tensorial affinities and this brings about a fundamental difference in that one obtains from this a geometric which is such that vectors now maintain not only their length but their angle as-well upon parallel transport. In § (6), we will provide the details of how in the NWG one obtains tensorial affinities from the conformal terms of the metric![]() . In the next section, we will present an important idea that is vital to the present unification, namely that the Riemann metric
. In the next section, we will present an important idea that is vital to the present unification, namely that the Riemann metric ![]() can be decomposed in such a manner that is now contains four and not ten free parameters.
can be decomposed in such a manner that is now contains four and not ten free parameters.
4. Decomposition of the Metric Tensor
In the present section we justify one of the major ideas of the present unified theory. This is the idea that the metric tensor can―logically, be decomposed in a manner that allows us to write down an equivalent Dirac equation in curved spacetime. The resulting decomposed metric is central to the final unified theory, it is so central that without it, one can not envisage obtaining the required correspondence of the present theory with experience.
That said, there are several curved spacetime versions of the Dirac equation (cf. [9] [10] [12] -[17] ). In our modest view; save for the introduction of a seemingly mysterious four vector potential![]() , what makes the curved spacetime version of the Dirac equations presented in the reading [18] stands-out over other attempts in that the method used in arriving at these curved spacetime Dirac equations [18] is exactly the same as that used by Professor [19] [20] . As will be demonstrated shortly, this method used in [18] appears to us as the most straight forward and logical manner in which to arrive a curved spacetime version of the Dirac equation. All that has been done in [18] is to decompose the general metric
, what makes the curved spacetime version of the Dirac equations presented in the reading [18] stands-out over other attempts in that the method used in arriving at these curved spacetime Dirac equations [18] is exactly the same as that used by Professor [19] [20] . As will be demonstrated shortly, this method used in [18] appears to us as the most straight forward and logical manner in which to arrive a curved spacetime version of the Dirac equation. All that has been done in [18] is to decompose the general metric ![]() in a manner that allows us to apply Professor Dirac [19] [20] ’s prescription at arriving at the Dirac equation.
in a manner that allows us to apply Professor Dirac [19] [20] ’s prescription at arriving at the Dirac equation.
Professor Dirac [19] [20] ’s original equation is arrived at from the Einstein momentum-energy equation, namely![]() , where
, where ![]() is the usual Minkowski metric,
is the usual Minkowski metric, ![]() are the four momentum and rest mass of the particle in question respectively and c is the usual speed of light in a vacuum. In curved spacetime, we know very well that the equation
are the four momentum and rest mass of the particle in question respectively and c is the usual speed of light in a vacuum. In curved spacetime, we know very well that the equation ![]() is given by
is given by ![]() where
where ![]() is the general metric of a curved spacetime. If a curved spacetime version of the Dirac equation is to be derived, it must be derived from the fundamental equation
is the general metric of a curved spacetime. If a curved spacetime version of the Dirac equation is to be derived, it must be derived from the fundamental equation ![]() in the same way the flat spacetime Dirac equation is derived from the fundamental equation
in the same way the flat spacetime Dirac equation is derived from the fundamental equation![]() . Professor Dirac derived his equation by taking the “square-root” of the equation
. Professor Dirac derived his equation by taking the “square-root” of the equation![]() . It is a fundamental mathematical fact that a two rank tensor (such as the metric tensor
. It is a fundamental mathematical fact that a two rank tensor (such as the metric tensor![]() ) can be written as a sum of the product of a vector
) can be written as a sum of the product of a vector![]() , i.e.:
, i.e.:
![]() (5)
(5)
where ![]() is the usual anti-commutator bracket,
is the usual anti-commutator bracket, ![]() are 4 × 4 matrices such that
are 4 × 4 matrices such that ![]() and
and
γ-matrices4 are 4 × 4 matrices defined such that:
![]() (6)
(6)
where ![]() is the 2 × 2 identity matrix,
is the 2 × 2 identity matrix, ![]() is the usual 2 × 2 Pauli matrices and the 0’s are 2 × 2 null matrices and
is the usual 2 × 2 Pauli matrices and the 0’s are 2 × 2 null matrices and ![]() such that for:
such that for:
![]() (7)
(7)
The index “a” is not an active index as are the Greek indices. This index labels a particular curvature of spacetime i.e. whether spacetime is flat5, positive or negatively curved. Written in full, the three metric tensors![]() ,
, ![]() and
and ![]() are given by:
are given by:
![]() (8)
(8)
![]() (9)
(9)
and the metric ![]() is related to
is related to ![]() by the transformation
by the transformation ![]() or
or![]() , that is to say:
, that is to say:
![]() (10)
(10)
Especially for a scientist and/or mathematician, there is little if anything they can do but accept facts as they
stand and present them-self. So doing, this means that the writing of ![]() as
as ![]() is to be
is to be
accepted as a legitimate mathematical fact for as long as ![]() is a tensor. Since
is a tensor. Since ![]() is a vector and the γ-ma- trices are all constant matrices,
is a vector and the γ-ma- trices are all constant matrices, ![]() is a tensor. Therefore, it follows that the equation
is a tensor. Therefore, it follows that the equation ![]() can
can
now be written as![]() . As clearly demonstrated in [18] , if we are to have the equation
. As clearly demonstrated in [18] , if we are to have the equation ![]() written in the decomposed form
written in the decomposed form![]() , and one where to fol-
, and one where to fol-
low Professor [19] [20] ’s original derivation method, they will arrive at the three curved spacetime Dirac equations, namely:
![]() (11)
(11)
It is not a difficult exercise to show that multiplication of (11) from the left hand-side by the conjugate opera-
tor ![]() leads us to the Klein-Gordon equation
leads us to the Klein-Gordon equation ![]() provided we have
provided we have
![]() . This condition
. This condition![]() , should be taken as a gauge condition restricting this four vector.
, should be taken as a gauge condition restricting this four vector.
As it stands, Equation (11) would be a horrible equation insofar as its solutions are concerned because the vector ![]() is expected to be a function of space and time i.e.
is expected to be a function of space and time i.e.![]() . Other than a numerical solution, there is no foreseeable way to obtain an exact solution is if that is the case. However, we found a way round the problem; we fortunately realised that this vector can actually be used to arrive at a general spin Dirac equation thereby drastically simplifying the equation so that it now is given by:
. Other than a numerical solution, there is no foreseeable way to obtain an exact solution is if that is the case. However, we found a way round the problem; we fortunately realised that this vector can actually be used to arrive at a general spin Dirac equation thereby drastically simplifying the equation so that it now is given by:
![]() (12)
(12)
where now ![]() and:
and:
![]() (13)
(13)
In Equation (12), the vector ![]() has completely disappeared from our midst thus drastically simplifying the resultant equation in the process [21] [22] .
has completely disappeared from our midst thus drastically simplifying the resultant equation in the process [21] [22] .
What we have done in the present section is to demonstrate that the metric tensor is susceptible to decomposition into a tensor field describable by four unique fields that form a relativistic four vector. In the GTR, the metric tensor exists as a compound mathematical object comprising ten unique fields. We shall take a leaf from the present exercise whereby we shall import it into the unified field theory that we hope to build. Despite the obvious similarities, the decomposition of the metric that we employ in the proposed unified theory is different from the decomposition carried out in the present section.
5. Riemann-Hilbert Space
The to be proposed all-encompassing Unified Field Theory (UFT) of all the forces of Nature is built on a spacetime that we have coined the Riemann-Hilbert Spacetime (RHS). Hereafter, when-ever we refer to the UFT, we mean the UFT presented herein. In the sections that follow, we shall succinctly describe the major highlights of RHS and in so doing, we are in actual fact describing the UFT itself. This spacetime has been dumbed the RHS because it is a hybrid Riemann space which has in it embedded Hilbert-objects. By Hilbert-objects, we mean the quantum mechanical wavefunction. The RHS is a modified Weyl space which Professor Einstein ruthlessly short-down when Professor Weyl tried to put forward his unified theory of gravitation and electromagnetism.
5.1. Line Element and Position Vector as 4 × 4 Objects
In the RHS, the entire structure of Riemann geometry is inherited in its complete form and is modified by replacing the metric with a new somewhat conformal metric ![]() which is such that
which is such that![]() , where
, where ![]() is a 4 × 4 matrix and the line element is such that:
is a 4 × 4 matrix and the line element is such that:
![]() (14)
(14)
where ![]() is the position of a particle on this spacetime and unlike in the ordinary space we are used to, this position vector (i.e.,
is the position of a particle on this spacetime and unlike in the ordinary space we are used to, this position vector (i.e.,![]() ) is a 4 × 4 matrix, that is to say,
) is a 4 × 4 matrix, that is to say, ![]() and the metric
and the metric ![]() is such that
is such that ![]() while
while ![]() is the usual zero rank position vector that we are used to. The vector
is the usual zero rank position vector that we are used to. The vector ![]() is a 4 × 4 objects. This vector
is a 4 × 4 objects. This vector ![]() is assumed to be:
is assumed to be:
1) Comprised of real elements.
2) Hermitian i.e.![]() .
.
5.2. Different Representations of the Metric
Now, we will add an extra index-![]() to the metric
to the metric![]() . We will do this by noticing that
. We will do this by noticing that ![]() which in-turn is such that
which in-turn is such that![]() . We know that we can always find a set of finitely many 4 × 4 unitary hermitian matrices
. We know that we can always find a set of finitely many 4 × 4 unitary hermitian matrices ![]() where
where![]() , such that
, such that![]() . Given this, it follows that
. Given this, it follows that![]() .
.
If we write![]() , then, we can write
, then, we can write ![]() as
as![]() . Therefore, from here-on,
. Therefore, from here-on,
the metric shall be written with the index-![]() and this index does not label components of the metric tensor but a representation of the of it.
and this index does not label components of the metric tensor but a representation of the of it.
Notice that we have placed the index-![]() in
in ![]() and
and ![]() in brackets. The reason for this is that the
in brackets. The reason for this is that the ![]() - indices label the components of the tensors
- indices label the components of the tensors ![]() and
and ![]() while “
while “![]() ” labels representations of these same tensors. We have done this to distinguish components of the tensor from their representations. This notation we shall use throughout this reading from here-on. There reader must take notice of this.
” labels representations of these same tensors. We have done this to distinguish components of the tensor from their representations. This notation we shall use throughout this reading from here-on. There reader must take notice of this.
Now, when finally we derive the Dirac equation in the separate future reading, it will be seen that the different representations of the metric ![]() lead to Universes that have different charge conjugation, parity and time reversal symmetries. Unlike in the Dirac theory where all these symmetries are upheld, some of the
lead to Universes that have different charge conjugation, parity and time reversal symmetries. Unlike in the Dirac theory where all these symmetries are upheld, some of the ![]() -represen- tations violate these symmetries. As is demonstrated in [23] , this presents us with a scenario and golden opportunity to possible explain why our present Universe seems to have a preponderance of matter over antimatter.
-represen- tations violate these symmetries. As is demonstrated in [23] , this presents us with a scenario and golden opportunity to possible explain why our present Universe seems to have a preponderance of matter over antimatter.
5.3. Unit Vector
Any space or spacetime must be endowed with unit vectors at each and every point of the continuum. The unit vectors on the RHS are variable, that is to say, if ![]() is the unit vector, then:
is the unit vector, then:
![]() (15)
(15)
where ![]() is a set of 4 × 4 matrices i.e.:
is a set of 4 × 4 matrices i.e.:
![]() (16)
(16)
In future reading where the Dirac equation will be derived from the soils of the present theory, it is shown how one can naturally harness from (15) the curved spacetime Dirac equations presented in [18] .
The position vector ![]() of a point on this spacetime continuum is such that
of a point on this spacetime continuum is such that![]() , so that
, so that![]() . Because
. Because ![]() and
and![]() , it is clear that
, it is clear that ![]() can not have a fixed value, hence the RHS has variable unit vectors. The direction and magnitude of these unit vectors on the RHS depend on their position
can not have a fixed value, hence the RHS has variable unit vectors. The direction and magnitude of these unit vectors on the RHS depend on their position![]() . This is a property that is unlike any other geometry except the so-called failed Weyl geometry [6] [9] [10] . The criticism of the great Professor Einstein on the so-called failed Weyl geometry does not apply to the present RHS.
. This is a property that is unlike any other geometry except the so-called failed Weyl geometry [6] [9] [10] . The criticism of the great Professor Einstein on the so-called failed Weyl geometry does not apply to the present RHS.
We must hasten to say that, whosoever seeks to discredit and bring down the present theory on the same basis as the great Professor Einstein did with Professor Weyl’s theory on the grounds that the line element ![]() is not invariant under a transformation of the coordinate or frame of reference, hence, certain absolute quantities, such as the spacing of atomic spectral lines and the Compton wavelength of an Electron for example, would change arbitrarily and thus have to depend on their prehistory; then, the rebuttal to this line of thought is that the proper time of any physical system is here not given by
is not invariant under a transformation of the coordinate or frame of reference, hence, certain absolute quantities, such as the spacing of atomic spectral lines and the Compton wavelength of an Electron for example, would change arbitrarily and thus have to depend on their prehistory; then, the rebuttal to this line of thought is that the proper time of any physical system is here not given by![]() , but by
, but by![]() . One must without fail remember that
. One must without fail remember that![]() ;
; ![]() is an invariant physical quantity while
is an invariant physical quantity while ![]() is not. Therefore, Professor Einstein’s agile criticism, while valid, it does not hold “any water” nor ground in the present scheme of things.
is not. Therefore, Professor Einstein’s agile criticism, while valid, it does not hold “any water” nor ground in the present scheme of things.
5.4. Some Remarks
An important point to note is that the metric ![]() and not
and not ![]() plays on the RHS the same role it plays on Riemann space i.e. the role of lowering and raising of indices. This, the reader must take note of, because it is what we shall use. Further, unlike on the Riemann space,
plays on the RHS the same role it plays on Riemann space i.e. the role of lowering and raising of indices. This, the reader must take note of, because it is what we shall use. Further, unlike on the Riemann space, ![]() , and not,
, and not,![]() .
.
As will be demonstrated in a future reading where the Dirac equation will be derived from the soils of the present theory, the field![]() , is actually the Dirac probability density function and is such that
, is actually the Dirac probability density function and is such that ![]() where
where ![]() is the Dirac four component wavefunction. So, the field
is the Dirac four component wavefunction. So, the field ![]() represent the material aspect of matter while the
represent the material aspect of matter while the ![]() via the four vector field
via the four vector field![]() , represent the force field aspect of matter. It is the object,
, represent the force field aspect of matter. It is the object, ![]() , that is the embedded Hilbert object we refereed to in the opening paragraph of the present section.
, that is the embedded Hilbert object we refereed to in the opening paragraph of the present section.
Now, in the next section i.e. in § (6), we will move to demonstrate that one can attain tensorial affiens. The attainment of tensorial affinities will allow us in § (7) to write down a general field equation for the RHS. In the § (8), we use the tensorial nature of the affinities to get reed of the non-liner aspect of the RHS. Having obtained non-linear field equations on the RHS, we show in § (9) that these field equations lead us to a familiar territory of Yang-Mills (YM) field equations and conservation laws. The resulting field equations as they stand appear at face-value to have the gravitational force outside of the whole scheme, leading to the feeling or notion that the present UFT is only a unified theory of the nuclear forces. We argue via a gravitomagnetic approach in § (11) that the gravitational force is very much part of the whole scheme. Further, in § (12), we show that one can derive the familiar geodesic equation of motion with the Lorentz-force term for both the electrical and gravitational forces.
6. Tensorial Affinities
If we replace the metric, ![]() , in Riemann geometry with a new metric,
, in Riemann geometry with a new metric, ![]() , which is such that,
, which is such that, ![]() , and maintain that,
, and maintain that, ![]() , so that Professor Einstein’s criticism of Professor Weyl’s theory is invalidated, then as shown in [5] , the resulting affine connection,
, so that Professor Einstein’s criticism of Professor Weyl’s theory is invalidated, then as shown in [5] , the resulting affine connection, ![]() , is such that,
, is such that, ![]() , where:
, where:
![]() (17)
(17)
In this new affine (17), the object, ![]() , is no longer a vector, it is such that,
, is no longer a vector, it is such that,![]() . Since
. Since![]() , is no longer a vector, the first and most important of all the improvements to be made on the RHS is that the role of the conformal object
, is no longer a vector, the first and most important of all the improvements to be made on the RHS is that the role of the conformal object ![]() now takes a new decisive and pivotal role. It is now required of it that the Weyl affine connection,
now takes a new decisive and pivotal role. It is now required of it that the Weyl affine connection, ![]() , must forcefully be constrained such that, at the end of the day―when all is said and done, and for all conditions of existence, the affine connection,
, must forcefully be constrained such that, at the end of the day―when all is said and done, and for all conditions of existence, the affine connection, ![]() , is, for better or worse, a tensor! Given that the three Christophel symbol,
, is, for better or worse, a tensor! Given that the three Christophel symbol, ![]() , naturally transforms as:
, naturally transforms as:
![]() (18)
(18)
then, it clearly follows that if, ![]() , were to transform as the Christoffel symbol, i.e.:
, were to transform as the Christoffel symbol, i.e.:
![]() (19)
(19)
the affine, ![]() , will be a tensor as per desideratum. If the Weyl connection,
, will be a tensor as per desideratum. If the Weyl connection, ![]() , is to transform as demanded in (19), then―invariably; the object,
, is to transform as demanded in (19), then―invariably; the object, ![]() , must transform as:
, must transform as:
![]() (20)
(20)
Thus―at any rate, ![]() can not be a vector. For this object
can not be a vector. For this object ![]() to transform as required in (20), the conformal term
to transform as required in (20), the conformal term ![]() must transform as follows:
must transform as follows:![]() , such that:
, such that:
![]() (21)
(21)
In this way―and this way alone; we attain the long sort tensorial affinities. So, the object ![]() is there so that we attain this pined desire for tensorial affinities.
is there so that we attain this pined desire for tensorial affinities.
It should be noted that nothing from within the RHS requires that the affinities be tensors. This is a requirement imposed exogenously by us because the RHS allows us to make such a choice without violating any of its marvellous structural properties. This reminds us of the words of Professor Einstein when he said that when constructing a theory, one must put themselves in the position of God6 and ask themselves the deepest and most enduring questions about physical and natural reality, such as:
“If I were God; how would I have created the Universe? Did God have a choice in creating the Universe?”
To these words of Professor Einstein, we add the following words:
“If He (God) did have a choice, what is that choice and; why that choice and not any other?”
Our pedestrian feeling on the issue of the Mind of God, His thoughts and choices is that all the constraints― more so the gauge conditions that we find necessary for our theories; the constraints that we impose on fundamental physical theories, these are most certainly God’s subtle thoughts which He employed in making the Universe. These exogenous impositions are there to attain a particular structure of the World. If any, who could have imposed these conditions from outside except the Creator Himself? This once again reminds us of the other of Professor Einstein’s wise words:
“I want to know how God created this World. I am not interested in this or that phenomenon, in the spectrum of this or that element. I want to know His thoughts; the rest are details.”
Perhaps, the Mind of God insofar as the architecture, design and building of the World is concerned, this might very well be hidden and revealed in the Universal World Geometry upon which the Universe is created and His thoughts in doing so (i.e., creating the World), in the gauge conditions and exogenous impositions on this Universal World Geometry; i.e., impositions that allow us to obtain exactly the conditions and laws of the present World. That is to say, are not these gauge conditions a sacrosanct signature of God’s sleight of hand and mind in creating a Universe of His choice? We leave the reader to ponder and ex-cogitate on this and the other deeper questions here raised above about physical and natural reality.
Now, back to the real World, the palatable World of ponderable facts. In the present section, we have demonstrated that one can achieve on the RHS tensorial affinities. In the next section, we shall now use this to deduce the major field equations for matter and energy of the RHS. From this equation, we are hopeful that all of reality―insofar and fundamental physical forces are concerned; must be harnessed forthwith. Before that, we need to do two things, the first is ask, what ![]() must be in-order that we obtain the desired transformation
must be in-order that we obtain the desired transformation ![]() and second, what gauge conditions if any can we deduce about the field
and second, what gauge conditions if any can we deduce about the field ![]() from our experience with Professor Maxwell’s Electrodynamics? We will start with the latter.
from our experience with Professor Maxwell’s Electrodynamics? We will start with the latter.
Professor Maxwell’s electrodynamic field tensor has the property of being traceless i.e.![]() . This property we will carry over to the present field tensor
. This property we will carry over to the present field tensor![]() , as we realise that we need this condition in-order to arrive at the desired equation, that is, we shall assume the following as a gauge condition for
, as we realise that we need this condition in-order to arrive at the desired equation, that is, we shall assume the following as a gauge condition for![]() :
:
![]() (22)
(22)
This gauge condition will lead us to the another gauge condition that we will present in (48). Other than the traceless property, Professor Maxwell’s field tensor also has the anti-symmetry property![]() . We shall
. We shall
not be generalizing this to the present field tensor![]() , as so doing requires that
, as so doing requires that![]() , and
, and
this leads to physically meaningless equations as this requires that the vector![]() , be a constant always. Clearly, having the vector
, be a constant always. Clearly, having the vector ![]() as a constant vector is not only meaningless, but rank nonsense especially for a UFT as the present, as this will lead to the trivial equation “0 = 0”.
as a constant vector is not only meaningless, but rank nonsense especially for a UFT as the present, as this will lead to the trivial equation “0 = 0”.
Now, if the function ![]() will lead to the desired transformation of the affinities, then, we have to ask the ques- tion, “What must
will lead to the desired transformation of the affinities, then, we have to ask the ques- tion, “What must ![]() be a function of in-order to have the desired properties?” Latter, the function
be a function of in-order to have the desired properties?” Latter, the function ![]() is expected to be identified with the probability density of the particle in question. If this function can be expressed in-terms of the field functions or variables, then, it would fit very well into the philosophy of Occam’s Razor of having the minimal possible variables in a theory. It is not difficult to work it out that if:
is expected to be identified with the probability density of the particle in question. If this function can be expressed in-terms of the field functions or variables, then, it would fit very well into the philosophy of Occam’s Razor of having the minimal possible variables in a theory. It is not difficult to work it out that if:
![]() (23)
(23)
then, ![]() will have the desired transformational properties such that
will have the desired transformational properties such that![]() , where
, where ![]() is given by (21) and the object
is given by (21) and the object ![]() transforms as given in (20). We shall forthwith and hereafter take
transforms as given in (20). We shall forthwith and hereafter take ![]() to be given by (23). What (23) really means is that the wave-function has here been expressed as a function of the variables of the geometry. It was one of Professor Einstein’s intuitive requirements for any unified theory that the wave-function ought to emerge as a part of the geometrical description of spacetime. In having the wave-function as a geometrical description, Professor Einstein hoped to reed QM of its seemingly inherent probabilistic nature.
to be given by (23). What (23) really means is that the wave-function has here been expressed as a function of the variables of the geometry. It was one of Professor Einstein’s intuitive requirements for any unified theory that the wave-function ought to emerge as a part of the geometrical description of spacetime. In having the wave-function as a geometrical description, Professor Einstein hoped to reed QM of its seemingly inherent probabilistic nature.
Be that it may, we―at any rate, do not believe the geometrical description of ![]() given in (23) will reed QM of its seemingly intrinsic and inherent probabilistic nature. To address this or to demonstrate the probabilistic nature of QM, this requires on its own, a fresh new monograph―thus, we shall not go any deeper than we have done here. Further, because
given in (23) will reed QM of its seemingly intrinsic and inherent probabilistic nature. To address this or to demonstrate the probabilistic nature of QM, this requires on its own, a fresh new monograph―thus, we shall not go any deeper than we have done here. Further, because ![]() is a 4 × 4 object, it follows that
is a 4 × 4 object, it follows that ![]() is also a 4 × 4 object too. If
is also a 4 × 4 object too. If ![]() is a 4 × 4 object, it follows that,
is a 4 × 4 object, it follows that, ![]() can not be a 4 × 1 object as is the case in the Dirac wave-function; it has to be a 4 × 4 array just as is the case with
can not be a 4 × 1 object as is the case in the Dirac wave-function; it has to be a 4 × 4 array just as is the case with![]() . Actually, it will become much more clear in § (13.2) that the wavefunction
. Actually, it will become much more clear in § (13.2) that the wavefunction ![]() will have to be a 4 × 4 object if we are to attain a four dimensional Yang-Mills theory on the RHS.
will have to be a 4 × 4 object if we are to attain a four dimensional Yang-Mills theory on the RHS.
7. General Field Equations
Riemann geometry is built on the idea of parallel transport of vectors along a given path. A good description of parallel transport is perhaps that by Professor John Baez7. Following him [i.e. Professor John Baez]; say one starts at the north pole holding a javelin that points horizontally in some direction, and they carry this javelin to the equator always keeping the javelin pointing “in as same a direction as possible”, subject to the constraint that it points horizontally, i.e., tangent to the Earth. In this scenario, we see that the idea is that we are taking “space” to be the 2-dimensional surface of the Earth and the javelin is the “little arrow” or “tangent vector”, which must remain tangent to “space”. After marching down to the equator and making a 90˚ turn at the equator and then marching along the equation until some-point along the equator where another 90˚ turn toward the north pole is made thus marching back up to the north pole, always keeping the javelin pointing horizontally and “in as same a direction as possible”. “Obviously”, because the surface of the Earth is curved, by the time one gets back to the north pole, the javelin will be pointing in a different direction. The javelin is said to have been parallel transported from its initial starting point to the final end point in one cycle of a closed circuit.
Parallel transport is an operation that takes a tangent vector and moves it along a path in space without turning it (relative to the space) or changing its length akin to the a person that carries a javelin as described above. In flat space, we can say that the transported vector is parallel to the original vector at every point along the path. In curved space as described above, the original and final vector after the parallel transport operation are not coincident and the change in this can be computed as will be done below and for this exposition, one can visit any good book on the GTR (cf. [24] , pp. 137-138).
As shown in Figure 1, if say we have a vector ![]() and we parallel transport it along a closed circuit ABCD in the order
and we parallel transport it along a closed circuit ABCD in the order ![]() then
then ![]() then
then ![]() and then finally
and then finally![]() , if the space in question has a non-zero curvature, upon arrival at its original location, the vector is no-longer equal to the original vector. The changes of this vector along these paths are:
, if the space in question has a non-zero curvature, upon arrival at its original location, the vector is no-longer equal to the original vector. The changes of this vector along these paths are:
![]() (24)
(24)
where, ![]() , and,
, and, ![]() , are evaluated at the location indicated in the parenthesis and the vector,
, are evaluated at the location indicated in the parenthesis and the vector, ![]() , is the vector along AB and likewise, the vector,
, is the vector along AB and likewise, the vector, ![]() , is the vector along, BC. Collecting these terms (i.e.
, is the vector along, BC. Collecting these terms (i.e. ![]() ), yields the overall change (
), yields the overall change (![]() ) suffered by,
) suffered by, ![]() , i.e.:
, i.e.:
![]() (25)
(25)
and by differentiating the quantities in the brackets, this further reduces to:
![]() (26)
(26)
and using the identities, ![]() , one arrives at:
, one arrives at:
![]()
Figure 1. Parallel transport: The vector V is parallel transported in a closed circuit. Upon arrival at its original position, the vector is not equal to the original vector and this is a result of the curvature of the space in question.
![]() (27)
(27)
This can be written compactly as:
![]() (28)
(28)
where, ![]() , is the Riemann curvature tensor. The above result is the important reason why for instructive purposes we have gone through all the above calculation, namely to find (via this exposition) the mathematical relationship that informs us of the change that occurs for a any given vector after parallel transport. In Riemann geometry, the affinities are not tensors and this leads to vectors altering their direction as they are parallel transported. A vector parallel transported along a closed circuit will return to its original position in such a way that its direction is no longer the same as its initial direction.
, is the Riemann curvature tensor. The above result is the important reason why for instructive purposes we have gone through all the above calculation, namely to find (via this exposition) the mathematical relationship that informs us of the change that occurs for a any given vector after parallel transport. In Riemann geometry, the affinities are not tensors and this leads to vectors altering their direction as they are parallel transported. A vector parallel transported along a closed circuit will return to its original position in such a way that its direction is no longer the same as its initial direction.
For a moment, let us shy-away from the abstract World of mathematics and pause a perdurable question to the reader, a question about the real World. Suppose one is in a freely falling laboratory and this laboratory moves in a gravitational field in a closed circuit such that the laboratory leaves a given point and latter it returns to the same-point and throughout its path at all points it is in free-fall. The best scenario is a laboratory orbiting a central massive, body. If in this laboratory we have a stationery object―do we (or does one) expect that after a complete orbit this object will have its motion altered? Or, does one expect that an object (inside the laboratory) that―say, has a specific momentum (relative to the laboratory) will after a complete circuit alter its momentum without any external force being applied to the free-falling system?
If this did happen, then Newton's first Law of Motion that defines inertia systems of reference is violated and it would mean that there is no such thing as an inertial system of reference; actually this renders the Principle of Equivalence obsolete. Surely, something must be wrong because the Principle of Equivalence can not be found in this wanting-state. We argue the reader to carefully go through the above argument to convince themselves of its correctness (or its incorrectness thereof). Whatever conclusion the reader will reach, it does not affect the final thesis being advanced namely that the affinities must be tensors. If they disagree with the above, it really does not matter as long as they agree that tonsorial affinities preserve both the angle and the magnitude of a vector under parallel transport.
In the above, we say this renders the Principle of Equivalence obsolete because for a system in free-fall like the laboratory above, according to this Principle of Equivalence; it is an inertial system throughout its journey thus we do not expect an object in an inertial system to alter its momentum without a force being applied to it. The non-preservation of angles during parallel transport in Riemann geometry is in violation of the Principle of Equivalence if it is understood that parallel transport takes place in a geodesic system of reference i.e., inertial systems of reference.
Naturally, we expect that for an observer inside the laboratory, they should observe a zero net change in the momentum. This, in the context of parallel transport of vectors, means that, such a spacetime will parallel transport vectors (in free-falling frames) in a manner such that after a complete circuit the parallel transported vector and the original vector, will still have the same magnitude and direction i.e.,![]() . Actually, this means that throughout its parallel transport, the magnitude and direction of the vector must be preserved. Riemann geometry does not preserve the angles but only the length of the vector under parallel transport. The only way to have both the angles and the length preserved is if the affinities are tensors and the curvature tensor of such a spacetime will be identically equal to zero. We have already discovered a geometry whose affinities are tensors. Since the RHS is obtained from the Riemann via the transformation,
. Actually, this means that throughout its parallel transport, the magnitude and direction of the vector must be preserved. Riemann geometry does not preserve the angles but only the length of the vector under parallel transport. The only way to have both the angles and the length preserved is if the affinities are tensors and the curvature tensor of such a spacetime will be identically equal to zero. We have already discovered a geometry whose affinities are tensors. Since the RHS is obtained from the Riemann via the transformation, ![]() , all we need to do now is to make the transformation:
, all we need to do now is to make the transformation:![]() , so that:
, so that:
![]() (29)
(29)
where:
![]() (30)
(30)
The fact that, ![]() , implies that:
, implies that:
![]() (31)
(31)
because![]() ,
, ![]() and
and![]() . The fact that,
. The fact that, ![]() , does not necessarily mean that,
, does not necessarily mean that,![]() . Equation (31) is a major field equation of the present theory. In comparison to the GTR, it has the same status as Professor Einstein’s field Equation (2). This is the equation that describes all the known (and unknown) forces that exist or can ever exist on the RHS. This seemingly colossal claim that (31) describes all of the known and unknown forces, we shall substantiate in the subsequent sections. In the next section, we shall take advantage of the tensorial nature of the affinities and choose a World geometry that is linear in the curvature tensor. As will be demonstrated in the section which follows thereafter, this choice―of a World geometry linear in the curvature tensor; appears to have a very strong correspondence with the physical and natural reality of the World we live in.
. Equation (31) is a major field equation of the present theory. In comparison to the GTR, it has the same status as Professor Einstein’s field Equation (2). This is the equation that describes all the known (and unknown) forces that exist or can ever exist on the RHS. This seemingly colossal claim that (31) describes all of the known and unknown forces, we shall substantiate in the subsequent sections. In the next section, we shall take advantage of the tensorial nature of the affinities and choose a World geometry that is linear in the curvature tensor. As will be demonstrated in the section which follows thereafter, this choice―of a World geometry linear in the curvature tensor; appears to have a very strong correspondence with the physical and natural reality of the World we live in.
8. Linear Riemann-Hilbert Space
Given that we have attained a geometry with tensorial affines, now is our time, this is our moment of exhalation, a moment to reap the sweetest fruits of our hard labour i.e., it is time to take the fullest advantage of the tensorial nature of the affinities. We now have the mathematical and physical prerogative, legitimacy and liberty to choose a spacetime where the non-linear terms vanish identically i.e., a spacetime such that, ![]() , and:
, and:
![]() (32)
(32)
Clearly and without any doubt, this fact that we have chosen a spacetime that is governed by the constraint (32), this means that in a single and triumphant moment of joy, we have just reed ourselves of the monstrous and troublesome non-linear terms in the Riemann tensor (30) because with this beautiful and elegant choice (32), they [non-linear terms] now vanish identically to become but footnotes of history. This means (31) now becomes:
![]() (33)
(33)
From (32), if we set![]() , we will have,
, we will have, ![]() , where
, where![]() . Now raising the index
. Now raising the index ![]() in the equation,
in the equation, ![]() , and contracting it with
, and contracting it with![]() , we will have:
, we will have:
![]() (34)
(34)
Now that we have a theory linear in the curvature tensor, a theory in which the non-linear terms vanish, we can use this to separate the Weyl terms from the Riemann terms. Weyl terms are here those terms associated with the affine vector ![]() and the Riemann terms are those terms associated with
and the Riemann terms are those terms associated with![]() . From the affine
. From the affine![]() , it follows that:
, it follows that:
![]() (35)
(35)
where:
![]() (36)
(36)
is the linear Riemann curvature tensor, and:
![]() (37)
(37)
is a curvature tensor that we shall call the Weyl curvature tensor. This Weyl curvature tensor is defined in terms of the material field![]() , it must represent the material field.
, it must represent the material field.
Now, from (33) and (35), it follows that:
![]() (38)
(38)
At this point―if it turns out the this theory proves to be a correct description of physical and natural reality; we have no doubt that if Professor Einstein where watching from above or from wherever in the intestacies of spacetime, he must be smiling endlessly because his life long endeavour was to derive8 the material tensor from pure geometry and not to insert it by the sleight of the mind and hand as he did with his gravitational field Equation (2). As his internationally acclaimed scientific biographer Abraham Pais graphically put it―Professor Einstein would look at his Equation (2) and greatly admire the left hand side which he would compare with marble―it was beautiful, pure and was a marvel sight for the artist as it was constructed from pure geometry; but when he [Professor Einstein] would look at the right hand side of this same equation; with equal passion, he was visited by deep melancholy sighs and feelings which made him loath the right hand side of his equation―he would compare this right handside with wood―it was ugly; with no end insight, Professor Einstein would moan time and again until his last breath on 13 April 1955.
His ultimate pine and goal thereof was to turn wood into marble, which meant deriving the material field from pure geometry. Professor Einstein wanted to find the final theory, this he pursued to the very end of life to a point that while on his death bed on April 13, 1955, instead of worrying about the imminent end of his fruitful life, he asked for a pen and his notes so that he could continue to work on the unified theory that he was working on at the time. It is sad to say that Professor Einstein never laid a fertile egg on this front―i.e., the front of unification.
Be that it may, it is without an iota of doubt that we say that, if what is before us proves itself to have a correspondence with physical and natural reality, then we can safely say we have achieved one of Professor Einstein’s goals to attaining the “Elicit Dream of a Final Theory” by deriving the material tensor from pure geometry―wood, one way or the other, has finally been turned into marble! This we are certain has been achieved in the present UFT. The only question is, “Does the theory correspond with physical and natural reality?” This we leave in hand of the reader so that they may be their own judge on the matter.
8.1. First Bianchi Field Equations
Now, we shall derive other field equations. We know that the Riemann curvature tensor satisfies the first Bianchi identity:
![]() (39)
(39)
From this first Bianachi identity and as as-well from (38), it follows that:
![]() (40)
(40)
The identity (40) leads to an important identity (which, for our purposes we shall call it a gauge condition). This identity (gauge condition) is obtained from (40) by contracting the index ![]() with
with![]() , that is to say, if for (40) we set
, that is to say, if for (40) we set![]() , one is led to:
, one is led to:
![]() (41)
(41)
When we arrive at (58), it shall become clear that the gauge condition (41) is necessary in-order for us to arrive at the familiar Maxwell-Proca equations of Electrodynamics.
8.2. Second Bianchi Field Equations
Now, we are are ready to derive our last set of field equations. We know that Riemann curvature tensor satisfies the second Bianchi identity:
![]() (42)
(42)
From this second Bianachi identity and as as-well from (38), it follows that:
![]() (43)
(43)
In the next section, we shall explore the Equations (38), (39), (40), (42) and (43) and from these equations, we shall see that one is able to obtain field equations that we are already familar with.
9. Resultant Field Equations
Before we go into the details of the present section, we must mention that, from here-on, we will now bring back the ![]() -representation index into our equations. We know that the Christophel affine
-representation index into our equations. We know that the Christophel affine![]() , is defined such that,
, is defined such that,
![]() , and that the metric,
, and that the metric, ![]() , has been define such that,
, has been define such that,![]() .
.
Thus, substituting this metric into the affine connection and then differentiating it as required by the differentials appearing in the affine, we obtain the following:
![]() (44)
(44)
Now, if we set:
![]() (45)
(45)
then, it follows from (44) and (45) that:
![]() (46)
(46)
In (45), the reader must take notice of the fact that the Greek index-![]() has now joined the index-
has now joined the index-![]() as part of the representation indices in the superscript of
as part of the representation indices in the superscript of![]() , and because of this, we have added the “dummy” Greek indices,
, and because of this, we have added the “dummy” Greek indices, ![]() and
and![]() , to
, to![]() , because of field tensors,
, because of field tensors, ![]() , and,
, and,![]() . Note that
. Note that![]() ; this is an important fact that needs to be remembered by the reader.
; this is an important fact that needs to be remembered by the reader.
Now, moving on; in the expression of the affine connection, ![]() , the term,
, the term, ![]() , is the sum of the Terms (II, III & V) in (44), while,
, is the sum of the Terms (II, III & V) in (44), while, ![]() , is a sum of the Terms (I, IV & VI) of the same equation. We will now write,
, is a sum of the Terms (I, IV & VI) of the same equation. We will now write, ![]() , as:
, as:
![]() (47)
(47)
Now that we have written the affine in terms of the field, ![]() , we are now ready to write down the source coupled and source free field equations. Already, the agile can already see the writing on the wall, that the field,
, we are now ready to write down the source coupled and source free field equations. Already, the agile can already see the writing on the wall, that the field, ![]() , as given in (45), is to be identified latter with the YM-force field.
, as given in (45), is to be identified latter with the YM-force field.
Before closing this section, we will write down a gauge condition that flows from the gauge condition (22) i.e.![]() . If (22) is to hold true, then, from (45), it follows that:
. If (22) is to hold true, then, from (45), it follows that:
![]() (48)
(48)
This implied gauge condition (48) will prove necessary in-order for us to arrive at the crucial equation (53).
9.1. Modified Lorenz Gauge
The Lorenz gauge condition (here represented by the relation![]() ) was introduced for the first time by the Danish mathematician and physicist―Professor Ludvig Valentin Lorenz (1829-1891), in 1867 [25] . For many years (including present day literature), this gauge has (and is) mistakenly been called the Lorentz gauge, after the great Dutch physicist―Professor Hendrik Antoon Lorentz (1853-1928), who also used it in his long paper in 1892 [26] . Fortunately for Professor Ludvig Valentin Lorenz, the story of the misattribution has recently been told in detail by cf. Jackson & Okun and Nevels & Chang-Seok [27] [28] .
) was introduced for the first time by the Danish mathematician and physicist―Professor Ludvig Valentin Lorenz (1829-1891), in 1867 [25] . For many years (including present day literature), this gauge has (and is) mistakenly been called the Lorentz gauge, after the great Dutch physicist―Professor Hendrik Antoon Lorentz (1853-1928), who also used it in his long paper in 1892 [26] . Fortunately for Professor Ludvig Valentin Lorenz, the story of the misattribution has recently been told in detail by cf. Jackson & Okun and Nevels & Chang-Seok [27] [28] .
For the present UFT―rather naturally than by the sleight of hand―the Lorenz gauge condition has been found necessary in-order that there is symmetry in the Greek indices of the resulting mathematical objects of the theory such as tensors e.g. for ![]() to be symmetric under the assumption that
to be symmetric under the assumption that![]() , it is absolutely necessary that the Lorenz gauge should hold (see [29] , p. 33). If particles are to have a non-zero mass in the proposed UFT, we find it necessary that we further modify the Lorenz gauge condition, so that it now reads:
, it is absolutely necessary that the Lorenz gauge should hold (see [29] , p. 33). If particles are to have a non-zero mass in the proposed UFT, we find it necessary that we further modify the Lorenz gauge condition, so that it now reads:
![]() (49)
(49)
where ![]() is a constant non-zero inherent and intrinsic physical quantity which is to be associated with the particle in question and as will become clear in § (9.3),
is a constant non-zero inherent and intrinsic physical quantity which is to be associated with the particle in question and as will become clear in § (9.3), ![]() is the mass of the particle. As long as
is the mass of the particle. As long as ![]() is a constant, the modified Lorenz gauge (49) serves the same purpose as the original Lorenz gauge
is a constant, the modified Lorenz gauge (49) serves the same purpose as the original Lorenz gauge![]() .
.
9.2. Source Free Field Equations
Now, we are going to deduce the source free field equations from the first Bianachi identities (39). We know
that![]() , and written in an expanded form in terms of the field tensor
, and written in an expanded form in terms of the field tensor![]() , its
, its
derivatives and in terms of the vector field![]() , we will have:
, we will have:
![]() (50)
(50)
Inserting ![]() into the second Bianachi identity (39), one obtains a sum of terms,
into the second Bianachi identity (39), one obtains a sum of terms, ![]() and
and ![]() cyclic in the indices
cyclic in the indices![]() . The equation or identity
. The equation or identity![]() , will only make sense if:
, will only make sense if:
![]() (51)
(51)
and:
![]() (52)
(52)
We will take (51) and (52) as general field equations. If we multiply (52) throughout by ![]() and then contract the indices
and then contract the indices ![]() and
and ![]() (i.e. set
(i.e. set![]() ), we will have:
), we will have:
![]() (53)
(53)
Further, if we multiply (53) throughout by ![]() and then contract the indices
and then contract the indices ![]() and
and ![]() (i.e. set
(i.e. set![]() ), we will have:
), we will have:
![]() (54)
(54)
therefore:
![]() (55)
(55)
We shall assume that only (55b) holds true and![]() . Because of the gauge condition (48), if
. Because of the gauge condition (48), if![]() , the resulting equations do not make sense at all―they, as aforementioned, would lead to the trivial equation “0 = 0”. We shall thus take (55b) as a sacrosanct gauge condition. This gauge condition (55b) will prove necessary in deriving the sourced field equation when we arrive at (69).
, the resulting equations do not make sense at all―they, as aforementioned, would lead to the trivial equation “0 = 0”. We shall thus take (55b) as a sacrosanct gauge condition. This gauge condition (55b) will prove necessary in deriving the sourced field equation when we arrive at (69).
Now, from (52), we will derive the source free field equations. If we multiply (52) throughout by ![]() and then contract the indices
and then contract the indices ![]() and
and ![]() (i.e. set
(i.e. set![]() ), we will have:
), we will have:
![]() (56)
(56)
In the framework of Maxwellian Electrodynamics, the above set of Equations (56) gives the exact source free field equations. It therefore follows that we have derived the first set of Maxwell’s equations, namely, the source free equations. This―to any searching mind, especially after a twenty year arduous journey of relentless searching; is certainly a reassuring development. One can take a breath of fresh air and walk straight to look out the window and hope to see a pristine blue-sky.
9.3. Source Coupled Field Equations
We shall now proceed to derive the source coupled field equations. This, we shall do by use of Equation (38) by contracting the indices ![]() and
and![]() , that is, we set,
, that is, we set, ![]() , so that the new equation is:
, so that the new equation is:
![]() (57)
(57)
First, we shall compute,![]() . It should not be difficult to deduce that:
. It should not be difficult to deduce that:
![]() (58)
(58)
where:
![]() (59)
(59)
where![]() . Soon, it shall become clear that
. Soon, it shall become clear that ![]() is a mass term―albeit, a Proca mass term. From the gauge condition (41) i.e., the condition that
is a mass term―albeit, a Proca mass term. From the gauge condition (41) i.e., the condition that![]() , if follows that (58) can now be written as:
, if follows that (58) can now be written as:
![]() (60)
(60)
The tensor ![]() is symmetric in its Greek indices. The term
is symmetric in its Greek indices. The term![]() , may at face value lead one to think that this term
, may at face value lead one to think that this term ![]() is not symmetric in the Greek indices, thus leading to an apparent contradiction. However, one must bare in mind that
is not symmetric in the Greek indices, thus leading to an apparent contradiction. However, one must bare in mind that![]() , thus we can write (60) as:
, thus we can write (60) as:
![]() (61)
(61)
in which case it becomes clear that ![]() is symmetric in its Greek indices. It is not difficult to deduce that the scalar
is symmetric in its Greek indices. It is not difficult to deduce that the scalar![]() , is such that:
, is such that:
![]() (62)
(62)
Now we proceed to compute![]() . In the case of,
. In the case of, ![]() , we will have:
, we will have:
![]() (63)
(63)
and the scalar![]() , is such that:
, is such that:
![]() (64)
(64)
Since![]() , and
, and![]() , it follows that:
, it follows that:
![]() (65)
(65)
therefore:
![]() (66)
(66)
Now, the source coupled field equations shall be derived from the following equation:
![]() (67)
(67)
Therefore, we need to compute ![]() and
and![]() . For this effort, we shall begin with
. For this effort, we shall begin with![]() , i.e.:
, i.e.:
![]() (68)
(68)
Now, in the representation indices, let us set ![]() for the Greek indices. This means that the above will reduce to:
for the Greek indices. This means that the above will reduce to:
![]() (69)
(69)
From the gauge condition (55b) i.e.![]() , it follows that (69) will reduce to:
, it follows that (69) will reduce to:
![]() (70)
(70)
This already looks very familiar―doesn’t it?
Now, let us proceed to calculate the left handside of (67) i.e.![]() . From (60), it follows that:
. From (60), it follows that:
![]() (71)
(71)
From the definition of ![]() as given in (23), it is not difficult to show that:
as given in (23), it is not difficult to show that:
![]() (72)
(72)
By inference from Maxwellian Electrodynamics, we know that, ![]() , where
, where ![]() is the four electrodynamic current. By way of analogy, the term,
is the four electrodynamic current. By way of analogy, the term, ![]() , must be a four current as-well i.e.,
, must be a four current as-well i.e.,![]() ; the minus sign has here been inserted for convenience. Accepting the foregoing, we are led to the term,
; the minus sign has here been inserted for convenience. Accepting the foregoing, we are led to the term, ![]() , now being given by:
, now being given by:
![]() (73)
(73)
Now, putting everything together i.e. from (67), (70) and (73), it follows that:
![]() (74)
(74)
In the framework of Electrodynamics, not only have we derived the source coupled equations of Professor Maxwell [30] , but the Maxwell-Proca Equations of Electrodynamics first proposed by the great Romanian physicist, Professor Alexandru Proca [31] -[33] , as an equation representing massive photons. This same equation was first explored by him in the subsequent years [34] -[40] and is today universally accepted as an equation representing massive gauge fields. In comparison to the Professor Proca’s theory; as equation (74) stands, it is now clear that ![]() must indeed be a mass term. It should be stated clearly that, besides the fact that this equation yields results that resonant with experience; the fundamental justification of Professor Proca’s modification does not exist and the present effort may very-well justify this seemingly ad hoc modification by Professor Proca.
must indeed be a mass term. It should be stated clearly that, besides the fact that this equation yields results that resonant with experience; the fundamental justification of Professor Proca’s modification does not exist and the present effort may very-well justify this seemingly ad hoc modification by Professor Proca.
Thus, in Equations (56) and (74), we have attained the desired set of equations that enable us to obtain―as a bare minimum―all of Professor Maxwell’s equations. Prima facie, the gravitational force appears to be absent from the present scheme. We will tackle this issue soon in the § (11). In the next subsection, we will have a look at the second Bianachi identities (42) and (43), from where we deduce some conservation laws.
9.4. Second Bianachi Identity Equations
We are now going to use the second Bianachi identities (42) and (43) to demonstrate the existence of a conserved four current from the field tensors, ![]() and
and![]() . Before we go into our calculation, we need to compute the following:
. Before we go into our calculation, we need to compute the following:
![]() (75)
(75)
For this, we are going to use Equation (18) that has been derived in the reading [41] , namely, the equation:
![]() (76)
(76)
As shown therein, this equation is necessary for there to exist massive long range and long lived photons. If this equation holds, it therefore follows that:
![]() (77)
(77)
Now, we can proceed to show the existence of a conserved four current from the field tensors, ![]() and
and![]() . We know from (42) that:
. We know from (42) that:
![]() (78)
(78)
and contracting the indices ![]() and
and![]() , we will have:
, we will have:
![]() (79)
(79)
We know also know from (43) that:
![]() (80)
(80)
and as above, contracting the indices ![]() and
and![]() , we will have:
, we will have:
![]() (81)
(81)
What the above equations imply is that the tensors ![]() and
and![]() , are conserved quantities. Further, the equation
, are conserved quantities. Further, the equation![]() , is telling us that:
, is telling us that:
![]() (82)
(82)
where ![]() is fundamental physical constant with the dimension of per unit length. Either
is fundamental physical constant with the dimension of per unit length. Either![]() ,
, ![]() or
or![]() .
.
10. Stocktaking
Though we are not done yet, it is perhaps time to take stock of what we have achieved thus far so that we bring some clarity and as-well so that the length of the road ahead may be made known and furthermore, so that the reader does not develop fatigue. Firstly, in-order to generate the desired field equations (i.e. 74 and 56) which surely have a resemblance with equations we that already know from experience, we have required a total of five gauge conditions and these gauge conditions are:
1) The first gauge condition is the Lorentz gauge![]() . This gauge condition is necessary for symmetry purposes e.g. for
. This gauge condition is necessary for symmetry purposes e.g. for ![]() (cf. [29] , p. 33).
(cf. [29] , p. 33).
2) The second gauge condition (22) has been imported from Maxwellian Electrodynamics and applied to the present theory i.e.![]() . This gauge is necessary in-order to get reed of terms that do not appear in the usual equations of both Maxwellian and YM-Dynamics.
. This gauge is necessary in-order to get reed of terms that do not appear in the usual equations of both Maxwellian and YM-Dynamics.
3) The third gauge condition (48) i.e.![]() ; is a consequence of the second gauge condition stated above. This gauge condition proves to be necessary in-order to get reed of terms that do not appear in the usual equations of both Maxwellian and YM-Dynamics.
; is a consequence of the second gauge condition stated above. This gauge condition proves to be necessary in-order to get reed of terms that do not appear in the usual equations of both Maxwellian and YM-Dynamics.
4) The fourth gauge condition (55) is,![]() ; like the other gauge conditions, this gauge condition proves to be necessary in-order to get reed of terms that do not appear in the usual equations of both Maxwellian and YM-Dynamics.
; like the other gauge conditions, this gauge condition proves to be necessary in-order to get reed of terms that do not appear in the usual equations of both Maxwellian and YM-Dynamics.
The field equations that we have produced seem to have nothing to do with gravitation but the nuclear forces. This obviously gives one the feeling that gravitation has now been shut out of the unification scheme i.e. all the other forces have willingly submitted to geometrization and gravitation has been shut out somehow. In the first two instalments [29] [42] [43] leading to the present version of the UFT, we noted this and we had to find some rather draconian means to fit gravitation into the scheme. This is set to change in the present instalment as we have found a natural way to include gravitation via Professor José Hera [44] ’s important Existence Theorem.
11. Gravitation and Gravitomagnetism
Professor José Hera [44] formulated―in our view; a very important Existence Theorem that states that, given any space and time-dependent localized scalar and vector sources satisfying the continuity equation―as is the case with electromagnetism; there exists in general, two retarded vector fields ![]() that satisfy a set of four field equations that are similar in nature and form to Maxwell’s equations. By applying the theorem to the usual electrical charge and current densities, the two retarded fields are identified with the electric
that satisfy a set of four field equations that are similar in nature and form to Maxwell’s equations. By applying the theorem to the usual electrical charge and current densities, the two retarded fields are identified with the electric ![]() and magnetic
and magnetic ![]() fields and the associated field equations with Maxwell’s equations i.e.
fields and the associated field equations with Maxwell’s equations i.e.![]() . In a nutshell, what Professor José Hera [44] proved is that, if
. In a nutshell, what Professor José Hera [44] proved is that, if ![]() is the charge density and J is the associated current corresponding to this charge, i.e.:
is the charge density and J is the associated current corresponding to this charge, i.e.:
![]() (83)
(83)
then, there must exist two corresponding fields, X and Y, that satisfy the following set of equations:
![]() (84)
(84)
![]() (85)
(85)
![]() (86)
(86)
![]() (87)
(87)
where![]() ,
, ![]() ,
, ![]() are arbitrary positive constants and are related to the speed of light c by the equation
are arbitrary positive constants and are related to the speed of light c by the equation![]() . In the case of electricity and magnetism, if X and Y are identified with the electric and magnetic fields respectively, then, we will have Professor Maxwell’s classical equations for Electrodynamics―in which case
. In the case of electricity and magnetism, if X and Y are identified with the electric and magnetic fields respectively, then, we will have Professor Maxwell’s classical equations for Electrodynamics―in which case![]() ,
, ![]() and
and![]() . In the case of electricity and magnetism, if X and Y are identified with the electric and magnetic fields respectively, then we have Professor Maxwell’s classical equations for Electrodynamics. Clearly, this axiomatic approach of deriving Maxwell’s field equations strongly suggests that electric charge conservation―and nothing else; can rightfully be considered to be the most basic and fundamental assumption underlying Professor Maxwell’s all-embellished and celebrated Equations of Electrodynamics.
. In the case of electricity and magnetism, if X and Y are identified with the electric and magnetic fields respectively, then we have Professor Maxwell’s classical equations for Electrodynamics. Clearly, this axiomatic approach of deriving Maxwell’s field equations strongly suggests that electric charge conservation―and nothing else; can rightfully be considered to be the most basic and fundamental assumption underlying Professor Maxwell’s all-embellished and celebrated Equations of Electrodynamics.
If―as is widely believed; the force of gravity is conveyed by mass, then, if the associated current (momentum) of this mass is conserved as given in (83), then, there must exist the two fields associated with mass and momentum. One of the fields is obviously the gravitational field g. The other must be a magnetic like force. Let us give this field the symbol Bg and let us call this the gravitational magnetic field and for short the g-magnetic field. What this means is that there must exist a similar set of Professor Maxwell's equations for gravitation. This phenomenon is typically called gravitomagnetism.
The first to consider the possibility of a formal analogy between gravitation and electromagnetism is Professor Maxwell himself, in his landmarking treatise on “A Dynamical Theory of the Electromagnetic Field” [30] . After failing to justify (to himself) the implied negative energies associated with the gravitational field, Professor Maxwell abandoned this line of thought [45] . Twenty eight years had to pass before Dr. Oliver Heaviside (1850-1925) reconsidered Professor Maxwell’s imaginative and brilliant but forgotten thoughts [46] [47] . Despite its brilliance and fit of imagination, both Professor Maxwell [30] and Dr. Oliver Heaviside [46] [47] ’s work was speculative in nature, with no real justification from the then known fundamental principles of either physics or logic but rather from the intuitive power of human reason and imagination. Only in recent times, has a justifiable fundamental physical basis for Professor Maxwell and Dr. Heaviside’s speculation (hereafter, the Maxwell-Heaviside Gravitomagnetic Theory) been heralded [44] [45] [48] . Presently, gravitomagnetism is accepted as first order approximation of Professor Einstein’s GTR [49] [50] .
Writing in his book “Causality, Electromagnetic Induction and Gravitation”, Professor Oleg D. Jefimenko (1922-2009) revived [48] this almost forgotten if not abandoned line of thought which most physicists now viewed as a pseudo-science because of lack of a real fundamental physical and theoretical justification save for the sheer power and wit of human intuition and imagination. Taking the work of Professor Jefimenko one important and crucial step further, Professor José Hera [44] formulated an important Existence Theorem stated above. It is this theorem that we now find to be not only pivotal but crucial in justifying the way in which we are now going to introduce gravitation on the realm, structure and edifice of the RHS.
Professor José Hera [44] did not consider gravitation in his work. However, this work can easily be extended not only to gravitation but to any field whose charge and corresponding current obeys the continuity equation. Assuming―as already stated above; that mass is identified with the gravitational charge of the body in question―as is the case in physics; and as-well assuming the conservation of mass and momentum, which in-turn means the conservation of gravitational charge, then, there must exist two vector fields (call them g and Bg) that satisfy a set of four Maxwell-type equations. These four equations describe what is known as gravitomagnetism. Gravitomagnetism is nothing but a formal analogy between Maxwell’s equations and the field equations of gravitation.
The problem with the issue of gravitomagnetism is that some have taken this to mean that the generated g-magnetic field must have an effect on electrically-laden bodies―no! This field, Bg, only couples to mass just as the magnetic field generated by electric currents couples to electrically-laden bodies. How then are we to introduce gravitational into the present scheme? If the gravitational phenomenon does take part in Maxwell-Hea- viside gravitomagnetism, then, there must exist a gravitomagnetic four vector, ![]() , just as there exist an electromagnetic four vector. A straight forward way to introduce the vector,
, just as there exist an electromagnetic four vector. A straight forward way to introduce the vector, ![]() , would be to split the vector,
, would be to split the vector, ![]() , into the sum of two vectors, the electromagnetic four vector,
, into the sum of two vectors, the electromagnetic four vector, ![]() , and the gravitomagnetic four vector,
, and the gravitomagnetic four vector, ![]() , i.e.:
, i.e.:
![]() (88)
(88)
where ![]() and
and ![]() are constants of superposition e.g.:
are constants of superposition e.g.:
![]() (89)
(89)
where in general ![]() such that
such that![]() . The vectors
. The vectors![]() ,
, ![]() and
and![]() , are such that:
, are such that:
![]() (90)
(90)
hence:
![]() (91)
(91)
and:
![]() (92)
(92)
Therefore, the Riemann metric![]() , is such that:
, is such that:
![]() (93)
(93)
where ![]() and
and![]() . The RHS metric i.e.,
. The RHS metric i.e., ![]() , is therefore given by:
, is therefore given by:
![]() (94)
(94)
and in-turn, the curvature tensor is given by:
![]() (95)
(95)
In the complete absence of electromagnetism (i.e.![]() ), the RHS is expected to maintain all of its properties, for this to be so, we must have for the gravitomagnetic curvature tensor
), the RHS is expected to maintain all of its properties, for this to be so, we must have for the gravitomagnetic curvature tensor![]() , at all times whether or not electromagnetism exists or not. This invariably means that
, at all times whether or not electromagnetism exists or not. This invariably means that![]() , at all times and for all conditions of existence, thus, it follows from the foregoing that the field equation for RHS where both electromagnetism and gravitomagnetism exist, we must have:
, at all times and for all conditions of existence, thus, it follows from the foregoing that the field equation for RHS where both electromagnetism and gravitomagnetism exist, we must have:
![]() (96)
(96)
Therefore, the resulting field equations for the electromagnetic sector of the RHS will be:
![]() (97)
(97)
while for the gravitomagnetic sector, the field equations will be:
![]() (98)
(98)
Therefore, herein, the same equations governing the electrical phenomenon govern the gravitational phenomenon in such a way that both are driven by two independent vectors which are sadly related to each other only by addition and the resulting mathematics thereof. The two sit side-by-side with no intimacy whatsoever. However, in a future reading, we shall propose a truce whereby we slip in a component of the gravitational magnetism into the electromagnetic phenomenon. Before that, let us derive first the geodesic equation of motion.
12. New Geodesic Equation
Let us now address the problem raised in § (2), i.e., the problem of the geodesic law namely that it is neither invariant nor covariant under a change of the system of coordinates and/or change in the reference system. As currently obtaining in the GTR, in order to derive the equation of motion, one needs to formulate this equation first in a Gaussian coordinate system and thereafter make a transformation to a coordinate system of their choice. As already said in § (2), this geodesic equation is in conflict with the very principle upon which the GTR is founded, namely the Principle of Relativity, which requires that one should be free to formulate the geodesic equation of motion in any legitimate coordinate system of their choice without having to be preferentially constrained to start from a Gaussian coordinate system. The geodesic law Equation (1) is derived from the Lagrangian:
![]() (99)
(99)
by inserting this into the Lagrangian equation of motion, namely:
![]() (100)
(100)
and thereafter making the necessary logical algebraic operations and manipulations. In the present, one must realise that the metric ![]() is that which is given rise to by a massive electrically laden particle whose mass and electrical charge are say
is that which is given rise to by a massive electrically laden particle whose mass and electrical charge are say ![]() and Q, respectively. Thus, we have both a gravitational and electrical field, hence, our geodesic equation of motion must be able to describe the trajectory of a massive electrically laden test particle. Given that the RHS’s metric is,
and Q, respectively. Thus, we have both a gravitational and electrical field, hence, our geodesic equation of motion must be able to describe the trajectory of a massive electrically laden test particle. Given that the RHS’s metric is, ![]() , one might think―that, as is the case with the GTR; the Lagrangian:
, one might think―that, as is the case with the GTR; the Lagrangian:
![]() (101)
(101)
will yield an appropriate equation of motion that agrees with experience in describing the trajectory of a massive electrically laden test particle in the vicinity of a massive electrical charged parent body. In the next few paragraphs, we shall shed some light on this issue whereby, we come up with a Lagrangian that leads to the appropriate equation that is in tandem with physical and natural reality.
In its bare form, Equation (1) has no natural provision for describing the trajectory of an electrically laden test particle. If the parent body, i.e., the body about which the electrically laden test particle describes its motion; is also carrying an electric charge, then, if Equation (1) is to describe the path of the electrically laden test particle, it (Equation (1)) will have to be modify outside of the confines of the GTR. What we want―or more appropriately, what is expected of a Universal World Geometry such as the RHS, is that the geodesic equation of motion for the RHS must have within the confines of the RHS, the provision for trajectories of electrically laden test particles.
If at all, how are we to attain such a geodesic equation capable of describing the trajectory of an electrically laden test particle in the vicinity of a massive electrically charged parent body? From (94), it is clear that the RHS metric, ![]() , is split between the electrical and gravitational components i.e.:
, is split between the electrical and gravitational components i.e.:![]() . It is logical that the electrical charge,
. It is logical that the electrical charge,![]() ; of the test particle must couple to the electrical component of the metric
; of the test particle must couple to the electrical component of the metric![]() , and likewise, the gravitational charge,
, and likewise, the gravitational charge,![]() ; of the test particle must couple to the electrical component of
; of the test particle must couple to the electrical component of![]() .
.
The suggestion coming from the fact that the metric ![]() has two separate components of the electrical and the gravitational, is that we must have two separate Lagrangians for the electrically laden test particle; Lagrangians that are conjoined by simple addition. Let these Lagrangians be:
has two separate components of the electrical and the gravitational, is that we must have two separate Lagrangians for the electrically laden test particle; Lagrangians that are conjoined by simple addition. Let these Lagrangians be:![]() , for the electrical component, and
, for the electrical component, and![]() , for the gravitational component, so that the resulting Lagrangian
, for the gravitational component, so that the resulting Lagrangian![]() , is such that
, is such that![]() . If
. If![]() , is the inertia mass of the electrically laden test particle, then, we find the following as the appropriate Lagrangians that result in a geodesic equation of motion that yields equations of motion that match with what we know from experience, i.e., for
, is the inertia mass of the electrically laden test particle, then, we find the following as the appropriate Lagrangians that result in a geodesic equation of motion that yields equations of motion that match with what we know from experience, i.e., for![]() , we propose:
, we propose:
![]() (102)
(102)
where![]() , and likewise, for
, and likewise, for![]() , we propose:
, we propose:
![]() (103)
(103)
where![]() , and the quantity
, and the quantity ![]() is expected to be a universal and fundamental physical “constant” with the units of mass per unit electrical charge, it is a constant that makes
is expected to be a universal and fundamental physical “constant” with the units of mass per unit electrical charge, it is a constant that makes ![]() a dimensionless parameter.
a dimensionless parameter.
Now, inserting![]() , into (100), and upon making the correct algebraic operations and manipulations, one is lead to the following geodesic equation of motion:
, into (100), and upon making the correct algebraic operations and manipulations, one is lead to the following geodesic equation of motion:
![]() (104)
(104)
where:
![]() (105)
(105)
is a tensorial affine for as long as the γ’s are all scalars. The tensor affinities ![]() and
and![]() , are such that:
, are such that:
![]() (106)
(106)
and like wise, we have![]() , such that:
, such that:
![]() (107)
(107)
Now, since the affine![]() , is a tensor, the problem of the geodesic equation highlighted in § (2) is solved if-and-only-if this affine tensor yields equations of motion which correspond with experience. To that end, we shall now move to show―as a way of justification of the potency and latent power of Equation (104)―that this equation, does indeed produce an equation that yields―in the absence of gravitation, the usual Lorentz equation of motion for a test particle in an ambient electromagnetic field. In the presence if an ambient gravitational field, this same equation yields the usual Newtonian gravitational equation of motion―albeit, with the all-important difference that new gravitomagneitc Lorentz terms surface; these new gravitomagneitc Lorentz terms are just as in the case of the electrical force.
, is a tensor, the problem of the geodesic equation highlighted in § (2) is solved if-and-only-if this affine tensor yields equations of motion which correspond with experience. To that end, we shall now move to show―as a way of justification of the potency and latent power of Equation (104)―that this equation, does indeed produce an equation that yields―in the absence of gravitation, the usual Lorentz equation of motion for a test particle in an ambient electromagnetic field. In the presence if an ambient gravitational field, this same equation yields the usual Newtonian gravitational equation of motion―albeit, with the all-important difference that new gravitomagneitc Lorentz terms surface; these new gravitomagneitc Lorentz terms are just as in the case of the electrical force.
Therefore, to first order approximation, (104) becomes:
![]() (108)
(108)
an assuming the following gauge conditions:
![]() (109)
(109)
then, (108) reduces to:
![]() (110)
(110)
Without the Gravitomagneto-Dynamics (GMD) component, the above equation is the acceptable Lorentz force law. The ![]() components of the GMD component give the usual equation of motion for a particle in a gravitational field with it supplemented a corresponding gravitomagnetic Lorentz term.
components of the GMD component give the usual equation of motion for a particle in a gravitational field with it supplemented a corresponding gravitomagnetic Lorentz term.
![]() (111)
(111)
The new term on the far right of (110) we have coined it the quantum force as it depends on the quantum probability amplitude![]() . We shall keep to our mission, that is, simple write down the equations and leave the exploration for latter to be done by ourselves and others who will see light in the work here presented. In the subsequent section, we shall now daringly move to make a proposal, a proposal that would bring some form of intimacy between the gravitational and electrical phenomenon.
. We shall keep to our mission, that is, simple write down the equations and leave the exploration for latter to be done by ourselves and others who will see light in the work here presented. In the subsequent section, we shall now daringly move to make a proposal, a proposal that would bring some form of intimacy between the gravitational and electrical phenomenon.
13. Global Symmetries and Yang-Mills Force Fields
In all its noble endeavours as presently understood, Yang-Mills (YM) theory [51] ―which was born out of the speculative work of two future Professors of physics, Chen-Ning Franklin Yang (b. 1922) and Robert Laurence Mills (1927-1999); this theory seeks to describe the behaviour of elementary particles using non-Abelian Lie Groups and it is at the nimbus and core of the unification theory of the Electromagnetic and the Weak force [i.e.,![]() ] of Professor Weinberg, Salam and Glashow [52] -[54] as-well as Quantum Chromodynamics (QCD) which obeys
] of Professor Weinberg, Salam and Glashow [52] -[54] as-well as Quantum Chromodynamics (QCD) which obeys ![]() symmetry and is the theory of the Strong force. Thus, YM-Theory forms the basis of the physicist’s current understanding of particle physics which is commonly refereed to as the Standard Model (SM). The question that we wish to ask and answer in this section is whether or not the present theory has within its fabric the ability to describe YM-Theory. The answer is yes, it has the ability to describe Yang-Mills Theory. We will not give a full demonstration of this, but only a glimpse of it. The exhibition of the full demonstration will be conducted in the accompanying and up-coming monograph.
symmetry and is the theory of the Strong force. Thus, YM-Theory forms the basis of the physicist’s current understanding of particle physics which is commonly refereed to as the Standard Model (SM). The question that we wish to ask and answer in this section is whether or not the present theory has within its fabric the ability to describe YM-Theory. The answer is yes, it has the ability to describe Yang-Mills Theory. We will not give a full demonstration of this, but only a glimpse of it. The exhibition of the full demonstration will be conducted in the accompanying and up-coming monograph.
13.1. Electromagnetism
Against the desideratum of the searching mind and very much to its chagrin, the natural picture emergent from the present UFT is one were the Universe is exclusively divided into two parts where one part is gravitational and the other electrical. In a separate future reading which tries to find intimacy between the electrical and gravitational phenomenon, we have proposed, more by the sleight of hand rather than from the naturalness of the theory a truce-like union between these gravitational and electrical components of the Universe. For the present section, we shall only consider the electrical component with the intent to demonstrate the existence of YM- Theory in the present UFT.
First we must realise that there are four fields in the representation F; and these are![]() ,
, ![]() ,
, ![]() and
and![]() . Depending on whether or not the non-Abelian component of
. Depending on whether or not the non-Abelian component of ![]() vanish, this field is either Abelian or
vanish, this field is either Abelian or
non-Abelian. If![]() , that is, the component
, that is, the component ![]() has no explicit time dependence, then the field
has no explicit time dependence, then the field
![]() , is Abelian. If like
, is Abelian. If like ![]() the components
the components ![]() have also no explicit time dependence,
have also no explicit time dependence,
then, from the definition of ![]() as given in (45), it follows that
as given in (45), it follows that ![]() must be an Abelien field since for this field, the non-Abelian component is forced to vanish. We expect that the field
must be an Abelien field since for this field, the non-Abelian component is forced to vanish. We expect that the field ![]() will have a clear space dependence thus making the fields
will have a clear space dependence thus making the fields ![]() to be the non-Abeliean YM-Fields.
to be the non-Abeliean YM-Fields.
What is interesting in all this is that, the electromagnetic field together with the resulting YM-Fields, these fields are all derived from the same vector field. This is unlike in the current SM were every field requires its own four vector field. In the scheme and core of the spirit of unification, this is considered to be the sought for unification were all the forces emerge from a singe field, they are different manifestations of the same field. The question now is, do the fields![]() ,
, ![]() and
and ![]() obey
obey ![]() or
or ![]() gauge invariance? If they do, then we have
gauge invariance? If they do, then we have ![]() and
and ![]() YM-Theory on the RHS. In the next subsection, we will show that any one of these fields―depending on the configuration thereof; can be shown to obey
YM-Theory on the RHS. In the next subsection, we will show that any one of these fields―depending on the configuration thereof; can be shown to obey![]() , albeit,
, albeit, ![]() on a four dimensional space.
on a four dimensional space.
13.2. Four Dimensional Yang-Mills Theory
We are now going to demonstrate that under certain conditions of existence on the RHS, there exists YM- Theory―a YM-Theory that is exactly as that found in the current SM, albeit, with the important difference that it is now a four dimensional YM-Theory. For this, let us generally consider the fields ![]() that transform according to some representation of a certain Lie Group G. That is, we shall consider the elements
that transform according to some representation of a certain Lie Group G. That is, we shall consider the elements ![]() to comprise a group. Because
to comprise a group. Because ![]() are 4 × 4 matrices, this means that, for every element of the Group G, we will have some 4 × 4 unitary matrices
are 4 × 4 matrices, this means that, for every element of the Group G, we will have some 4 × 4 unitary matrices![]() ; these matrices
; these matrices ![]() satisfy the same multiplication rules as the corresponding elements of G. Further, because the elements
satisfy the same multiplication rules as the corresponding elements of G. Further, because the elements ![]() are 4 × 4 matrices, they must submit to some decomposition were the wave function
are 4 × 4 matrices, they must submit to some decomposition were the wave function ![]() and the scalar and vector product
and the scalar and vector product ![]() can be written as the direct sum of subspaces of the Group G as follows:
can be written as the direct sum of subspaces of the Group G as follows:
![]() (112)
(112)
![]() (113)
(113)
where the q’s are real or complex numbers which are constraint by the usual wave-function normalization condition, namely ![]() (and as-well by the fact that
(and as-well by the fact that![]() ) in such a way that:
) in such a way that:
![]() (114)
(114)
where in the ordinary picture of QM, one can view the q’s in the same way one views the probability amplitudes
in quantum superposition i.e. in-ordinary QM, we have ![]() where
where ![]() is a quantum state function
is a quantum state function
and ![]() are sub-states of the system and cj are probability amplitudes. The objects
are sub-states of the system and cj are probability amplitudes. The objects ![]() are 4 × 4 matrices and are known as the generators of the Group G and they satisfy the following Lie Algebra9:
are 4 × 4 matrices and are known as the generators of the Group G and they satisfy the following Lie Algebra9:
![]() (115)
(115)
where ![]() is a set of structural constants peculiar to the Lie Group under consideration. The generators of the group are defined by the representation appropriate for the gauge Group G under consideration. Substituting (112) and (113) into (15), we obtain:
is a set of structural constants peculiar to the Lie Group under consideration. The generators of the group are defined by the representation appropriate for the gauge Group G under consideration. Substituting (112) and (113) into (15), we obtain:
![]() (116)
(116)
where:
![]() (117)
(117)
Just like![]() , the metric that emerges from (116) is decomposable and in its decomposed form, it is given by:
, the metric that emerges from (116) is decomposable and in its decomposed form, it is given by:
![]() (118)
(118)
where:
![]() (119)
(119)
It is very important to note at this point that if the wavefunction ![]() were a 4 × 1 object and not a 4 × 4 object as is the case in the present, then, it would have been impossible to decompose the metric in a manner that we have just done in (118). As will become clear shortly, this decomposition is a sine qua non in-order for the attainment of YM-Theory on the RHS.
were a 4 × 1 object and not a 4 × 4 object as is the case in the present, then, it would have been impossible to decompose the metric in a manner that we have just done in (118). As will become clear shortly, this decomposition is a sine qua non in-order for the attainment of YM-Theory on the RHS.
Now we come to the most crucial part on our “sojourn to demonstrate” the existence of YM-Theory on the RHS. Some may consider and ultimately accuse the step that we are about to take as a deliberate and artificial insemination of a condition into the theory so that the theory matches with experience. We see no problem with fixing a theory so as to match with experience. Like Professor Einstein’s GTR, most people would demand of a theory to be constrained by its internal and natural logic in-order to match with physical and natural reality. We ask you the reader:
Insofar as adoption is concerned, what would you do if you realised that there is an absolutely necessary condition not naturally found in the domains and confines of your theory, a condition that would make the theory beautifully match with experience? Would you not impose this condition by assuming it be a vital but (an as-yet) naturally unjustified ingredient of the theory?
Rather sceptically, fixation is largely viewed by the better majority of researchers as some form of “cheating” so as to arrive at the correct or desired answer. If anything, we are of the benevolent view that what one must ask after fixing a theory to match with experience is the following question:
What―if any; does this fixation tell us about the Laws of Physics in relation to physical and natural reality?
Before answering this question ourselves, let us write down the ansatz condition that we feel leads us to field equations that have a sure correspondence with the equations that we already known from experience―i.e., the equations of YM-Theory as they appear in the current SM. We find that if the following condition:
![]() (120)
(120)
is adopted (or assumed) and is taken as a fundamental gauge condition were ![]() are the associated coupling constants corresponding to the fields
are the associated coupling constants corresponding to the fields![]() , then, we will obtain all of YM-Theory on the RHS―albeit―a four dimensional YM-Theory which is much richer in content and meaning than the currently obtaining YM-Theory. In (120) above (and hereafter), the raised ik-indices in the structural constants
, then, we will obtain all of YM-Theory on the RHS―albeit―a four dimensional YM-Theory which is much richer in content and meaning than the currently obtaining YM-Theory. In (120) above (and hereafter), the raised ik-indices in the structural constants ![]() sum-up together with the ik-indices in the product
sum-up together with the ik-indices in the product![]() , just as is the case in the Einstein summation convention.
, just as is the case in the Einstein summation convention.
Notice that the ik-indices of ![]() in the middle term of (120) are not raised (i.e.,
in the middle term of (120) are not raised (i.e.,![]() ) while in the last part of this equation, they have been raised i.e.
) while in the last part of this equation, they have been raised i.e.![]() . We have raised the ik-indices of
. We have raised the ik-indices of ![]() to indicate summation in the usual Einstein summation convention. It is this raising of the ik-indices that enabled us to do away with the double summation signs appearing in the middle part of (120).
to indicate summation in the usual Einstein summation convention. It is this raising of the ik-indices that enabled us to do away with the double summation signs appearing in the middle part of (120).
Now, with this gauge condition (120) given, it follows that the field (45) will now be given by ![]() , where:
, where:
![]() (121)
(121)
In form and structure, this field is the usual YM-Field as we know it―albeit―a YM-Field whose ![]() -entries or elements are 4 × 4 matrices.
-entries or elements are 4 × 4 matrices.
Now, substituting (112) and (113) into (98), the resulting field equations:
![]() (122)
(122)
In (122), we have also written the resulting field equation for the gravitational and electrodynamic field. These equations surely lead to the following corresponding equations for the sub-particles![]() :
:
![]() (123)
(123)
Now, if at the most fundamental level of reality all the physics of the World is embodied in the field equations (122) and (123) [or (74) and (56)], then, the following transformations will leave all of the physics of the World invariant:
![]() (124)
(124)
where:
![]() (125)
(125)
is a hermitian unitary matrix which is such that![]() , and
, and ![]() is some 4 × 4 function that depends on
is some 4 × 4 function that depends on ![]() and this function is such that is anti-commutes with the the vector
and this function is such that is anti-commutes with the the vector![]() , that is to say:
, that is to say:
![]() (126)
(126)
While the transformations (124) will leave all of the physics of the World invariant, the transformation (124b) will alter the geometry of the sub-particles and as-well that of the particles themselves. In relation to the question that we paused earlier about the fixation of the theory to match with experience i.e. the question “What this fixing tells us about the Laws of Physics in relation to physical and natural reality?”, we now realise that this fixation is telling us that one can alter the geometry (via the alteration of the metric![]() ) of a particle without affecting the resulting physics thereof. This alteration that leaves the entire physics of the World invariant is that embodied in the arcane and beautiful mathematics of Lie Groups. This therefore suggests that particles may very will be undergoing a constant random changes in their geometries in-accordance with the mathematics of Lie Groups in such a way that from a physics stand-point, one can never notice this constant random change in the geometry of the particle.
) of a particle without affecting the resulting physics thereof. This alteration that leaves the entire physics of the World invariant is that embodied in the arcane and beautiful mathematics of Lie Groups. This therefore suggests that particles may very will be undergoing a constant random changes in their geometries in-accordance with the mathematics of Lie Groups in such a way that from a physics stand-point, one can never notice this constant random change in the geometry of the particle.
Thus, to justify the fixation (120) here-made without any prior knowledge that Nature employs YM-Theory in exactly the manner it does as we know, one would have to ask themselves the ansatz-type question:
What condition exists―if any; and is there to be imposed upon the RHS in such a manner that one can somewhat in an arbitrary, somewhat willy-nilly and willy-wally fashion, alter the geometry of a particle without affecting the resulting physics thereof?
The answer would be the imposition of the gauge condition (120); it is a condition which for better and/or for worse, is to be adhered to by the vector fields,![]() . Whence, if―truly; the RHS is the Fundamental and Universal Geometry of the World, then, according to all that we know at present, it would appear as though YM- Theory as presently understood, comes about as an exogenous imposition and not a natural occurrence on the RHS. Thus, we see here that to Professor Einstein’s all-daring question of whether or not the Good Lord had a choice in making the Universe, He [God] very well might have had a choice because the gauge condition (120) is a choice that seems to have been tailor made by Whosoever created the World and all therein. If anything, this condition (120) is a sure finger print of the Divine and Sacrosanct Tailor of the Universe. It is very much possible that if we knew much more than we know now, this condition (120) may turn-out to be a natural occurrence on the RHS, in which case, it would invariably mean that God may not have had a choice in creating a Universe governed by the mathematics of YM-Theory or Lie Groups. At present, we see no way of naturally harnessing it [condition (120)] from the RHS except by way of the sleight of hand were we have had to equanimously and gently impose it from outside.
. Whence, if―truly; the RHS is the Fundamental and Universal Geometry of the World, then, according to all that we know at present, it would appear as though YM- Theory as presently understood, comes about as an exogenous imposition and not a natural occurrence on the RHS. Thus, we see here that to Professor Einstein’s all-daring question of whether or not the Good Lord had a choice in making the Universe, He [God] very well might have had a choice because the gauge condition (120) is a choice that seems to have been tailor made by Whosoever created the World and all therein. If anything, this condition (120) is a sure finger print of the Divine and Sacrosanct Tailor of the Universe. It is very much possible that if we knew much more than we know now, this condition (120) may turn-out to be a natural occurrence on the RHS, in which case, it would invariably mean that God may not have had a choice in creating a Universe governed by the mathematics of YM-Theory or Lie Groups. At present, we see no way of naturally harnessing it [condition (120)] from the RHS except by way of the sleight of hand were we have had to equanimously and gently impose it from outside.
14. Discussion
We cannot possibly know whether or not the Good Lord looks down from above at our present endeavour and laughs if not scoff at it, that perhaps in all the twenty years (1994-2014) of the relentless and unflinching labour that we have put up in-order to attain the present unified theory, He has led us up the garden path on a sure blind alley. Be that it may, we surely must (unflinchingly)―for the sack of posterity; be bold enough as to express our true heartfelt confidence that the New Universal World Geometry (the RHS) here discovered most certainly describes our World or will in the immediate future prove to do exactly that. If experience proves otherwise―then, without an iota or dot of doubt; at least some elements of the present endeavour will surely percolate significantly into the Final Universal World Geometry to be discovered in the future by others.
The present UFT is built on what is supposed to be Professor Weyl’s fail idea [6] of adding a conformal term to the Riemann metric. Unlike Professor Weyl, we have demanded of this conformal term to yield for us tensorial affinities. Coupled with the idea of decomposing the metric into a product of a four vector, we have shown that one can obtain all the equations associated with Yang-Mills Theory, albeit, the resulting objects are 4 × 4 matrices. In this new UFT, it appears that gravitation may very well be explained by the very same mathematics that governs the nuclear forces. While the same mathematics applicable to the nuclear forces may apply to gravitation, the nuclear and gravitational forces seem to have no unification―i.e., intimacy and reciprocal action whereby one forces is inter-convertible into the other as initially desired by proponents of unification theories.
We should mention here that in building the present UFT, we have not made reference to the literature on unified field theories in the intervening years 1918-2014 and the reason for this being that we have have had to go back to 1918 and built our theory from the debris of Professor Weyl’s supposed failed unification effort. In the end, the final equations strongly appear to resemble currently accepted equations describing the nuclear forces. Because of this, we feel that the present work―if proved correct, may be pointing to the fact that, in our effort to arriving at the final theory, we may very well have taken the “wrong” theoretical route because our theories in building the theory of nuclear force have been predominately shaped by results from experiments rather than from theory. From a theoretical standpoint, it appears we have been trying to glue together general relativity and quantum mechanics using only logical connections and reasoning. In that effort to glue these two great theories together, we have respectively held them to be sacrosanct leading us to seeking a self consistent manner to glue them together while preserving their independent realities.
Basing on our true heartfelt confidence, we must say that, what is before us so strongly seems to point to the fact that the whole of physical phenomenon may now be derived from a single Universal World Geometry that obeys the Universal World Law beholden to the principle presaged in reading [29] (p. 13), namely that:
Generalized Principle of Equivalence: Physical Laws have the same form in all equivalent reference systems independently of the coordinate system used to express them and the complete physical state or physical description of an event emerging from these laws in the respective reference systems must remain absolutely and independently unaltered―i.e., invariant and congruent; by the transition to a new coordinate system.
We hearty, sincerely and in all probity believe that we have herein shown that it is possible to describe all the known forces of Nature on a four dimensional geometric theory that needs not the addition of extra dimensions as is the case with string and string related theories which today predominately stand on the beacon and chief echelons of unification as the most favoured/promising theories. Although a lot of work is still to be done as mentioned in the penultimate of the introduction section that two volumes each spanning about 200 pages are at an advanced stage of preparation, in our most humble and modest opinion, we believe that the present attempt is a significant contribution to the endeavour of the unification program of physics. We are of the strong opinion that the reader should be their own judge. We shall state a few main points that lead us to believe that the present attempt is a significant contribution to the endeavour of the unification program of physics.
First, we know that in Riemann geometry and as-well in the GTR, the metric tensor is described by ten different potentials and in-turn these potentials describe the gravitational field. On the RHS, the metric tensor is described by just four different potentials and not ten and these potentials describe both the gravitational, electromagnetic and nuclear and sub-nuclear fields. At the very least, this surely is a paradigm shift which is a much more simpler model of spacetime and matter that the most promising models! The RHS on which the present theory is founded, is different from Riemann spacetime in that the unit vectors of the RHS are variable at all points on this continuum. This property of the RHS that it has variable unit vectors make it fall into the category of Professor Weyl’s brilliant but failed geometry, but the RHS is different because the affinities are tensors; the meaning of which is that vectors do not change their length and angles under parallel transport.
We note that while the gravitational force has here been brought under the same roof with the nuclear forces, it is not unified with these forces in a manner Professor Michael Faraday had hoped, i.e., it being inter-convert- ible to other forces just as the electronic and magnetic forces are inter-convertible into one another. It is not even what Professor Einstein had envisaged in his 1929 interview with the journal Nature when he said [55]
“Now, but only now, we know that the force which moves Electrons in their ellipses about the nuclei of the atom is the same force which moves our Earth in its annual course about the Sun, and it is the same force which brings to us the rays of light and heat which make life possible upon this planet.”
Professor Einstein said these words when he was describing his then proposed final theory on distant parallelism [56] that latter proved to have no resemblance with physical and natural reality as we know it.
It strongly appears that we have been able to achieve one thing that Professor Einstein sought in a unified theory, i.e., he envisioned the material field ![]() being part and parcel of the fabric of spacetime. On this, i.e. his vision of the final theory, Professor Einstein is quoted as having said that the left handside of his equation is “like marble and the right handside is like wood” and that he found wood so ugly that his dream was to turn wood into marble. These feelings of Professor Einstein against his own GTR are better summed up in his own words in a letter to Father Georges Lemaitre (1894-1966) the Belgian Roman Catholic Priest on September 26, 1947:
being part and parcel of the fabric of spacetime. On this, i.e. his vision of the final theory, Professor Einstein is quoted as having said that the left handside of his equation is “like marble and the right handside is like wood” and that he found wood so ugly that his dream was to turn wood into marble. These feelings of Professor Einstein against his own GTR are better summed up in his own words in a letter to Father Georges Lemaitre (1894-1966) the Belgian Roman Catholic Priest on September 26, 1947:
I have found it very ugly that the field equation should be composed of two logically independent terms which are connected by addition. About justification of such feelings concerning logical simplicity is to difficult to argue. I can not help to feel [sorry] and I am unable to believe that such an ugly thing should be realised in Nature.
If anything, we consider that our ideas of a UFT have here been fully and well formulated. What lies ahead is to determine the precise nature of the theory via a rigours mathematical study against the background of our experience. The theory certainly contains tensor equations and the quantum theory of the Standard Model is a part of it. We could like to close with the words from the great Professor Einstein:
In light of knowledge attained, the happy achievement seems almost a matter of course, and any intelligent student can grasp it without too much trouble. But the years of anxious searching in the dark, with their intense longing, their alterations of confidence and exhaustion and the final emergence into the light―only those who have experienced it can understand it.
In addition to the depth of Professor Einstein’s words which are sure born out of true experience, we must hasten to add that in the pursuit of new knowledge, one ought to have the necessary “iron spine” to put up, and ultimately stand in the way of rebuke and discouragement from seemingly established professors (and eminent personalities), who, on their usual course or discourse, vehemently reject the new in-favour of maintaining the old, for it is about the only thing they have come to know and are thus only prepared to have that of old―and that alone; as the only true and purest wisdom of the World. The foremost duty to all of humanity―i.e., past, present and posterity; of the young, curious and the searching mind, is to vehicle and usher in new ideas procured from the lofty vineyard of the purest and finest of their thoughts. Most at times, this rebuke and discouragement springs from pure prejudice. Whatever the reason or reasons may be, the young, curious, zestful and searching mind must never tire, yield, give-up nor give-in, but continue un-diverted on its course, destiny and path―leading to newer depths; knowing that persistence―sure―yields its rewards, when one refuses to quit!
15. Conclusions
Assuming the correctness or acceptability of the ideas presented herein, we hereby make the following conclusions:
1) It is our feeling that a unified field theory of all the forces of Nature may very well have been achieved in the present instalment. Despite the plethora of work that lies ahead, we can―in the meantime hope that our readers will see light in what we have presented and that they may take part in the completion of the theory. We are certain that the completion of this theory can not be the effort of a single mind, but that of many minds working together.
2) The electrical and gravitational phenomenon have herein not been unified in a manner as was initially envisaged by a great many researchers e.g. notably Professor Faraday and Einstein; were a reciprocal action and interplay between the two fields has been highly anticipated. No, the two fields here seat harmoniously side-by- side in a quasi-independent manner on the RHS. We should say that, we also expected the final theory to give a reciprocal action and interplay between the electrical and gravitational phenomenon, but alas! Nature has Her own ways; this is not the case here and we can not force it to happen but rather accept what is on the table. If anything, we can only measure the present theory against the background of our experience to see if it has any bearing and correspondence with physical and natural reality as we come to know it.
3) A tensor affine theory that includes all the known force fields of the World has here been achieved on a four-dimensional continuum of spacetime without the need for extra dimensions. In relation to present efforts that employ extra dimension (i.e., string and string-related theories) and stand at the highest echelons of promise as the most promising unified theories, the attainment here of a unified theory which includes all the forces of Nature on a four-dimensional continuum of spacetime, is but a tremendous simplification. If correct, it is sure a great leap forward.
4) A geodesic equation that does not suffer the set back of needing preferred coordinate and reference systems has herein been achieved via the attainment of the tensorial affinities. The resulting geodesic equation has Lorentz terms for both the electrical and gravitational phenomenon. Besides, it has some extra new terms that need to be explored. This may very well explain some of the gravitational anomalies in the Solar system and as-well that of the flat rotation curves of spiral galaxies which has led to the darkmatter hypothesis.
5) Gravitomagnetism which emerges from Professor Einstein’s GTR as a first order approximation emerges in the present via Professor José Hera [44] ’s Existence Theorem as an exact physical phenomenon. The emergent gravitomagnetic phenomenon is exactly that which was envisaged by Professor Maxwell [30] and Dr. Heaviside [46] [47] many score years ago.
6) Professor Einstein’s gravitational waves which are―to first order approximation; vibrations of the Riemann metric ![]() and were predicted in 1916 at the inception of his GTR and have so far escaped direct detection by the finest instruments ever built; these gravitational waves may―sadly―not exist if the present theory stands the ruthless test of experience. Instead, Maxwell-Heaviside Gravitomagnetic waves analogous to electromagnetic waves are what may exist, should the present prove worthwhile.
and were predicted in 1916 at the inception of his GTR and have so far escaped direct detection by the finest instruments ever built; these gravitational waves may―sadly―not exist if the present theory stands the ruthless test of experience. Instead, Maxwell-Heaviside Gravitomagnetic waves analogous to electromagnetic waves are what may exist, should the present prove worthwhile.
7) The present theory is free from singularities for as long as ![]() and
and ![]() are non-singular. Actually, the present theory very readily provides for
are non-singular. Actually, the present theory very readily provides for ![]() and
and ![]() to be non-singular for all conditions of experience and existence. If this is the case, then, Professor Einstein’s black-holes which have so far escaped direct detection, may not exist. Yes, regions of extreme curvature are predicted to exist by the theory, but this will not lead to singular black-holes, but to regions of extreme curvature.
to be non-singular for all conditions of experience and existence. If this is the case, then, Professor Einstein’s black-holes which have so far escaped direct detection, may not exist. Yes, regions of extreme curvature are predicted to exist by the theory, but this will not lead to singular black-holes, but to regions of extreme curvature.
8) All the particles in Nature are predicted by the present theory to have a non-zero mass. This includes the photon and the neutrino―these must have mass, just as is the case with all other particles in Nature. This as well includes all gauge bosons. The idea of massive photons is given attention in the readings [41] [57] .
9) It should be stated clearly that, besides the fact that Professor Proca’s theory of massive gauge fields yields results that are in complete resonance with experience; the fundamental theoretical justification of this modification of Maxwellian Electrodynamics does not exist―actually no clearly visible effort in the available literature has been made to seek the fundamental theoretical justification for the Proca theory. The present effort may very-well be the required justification for this brilliant but seemingly ad hoc modification of Professor Proca. If this is the case that the present theory is surely a fundamental theoretical justification for the Proca theory, then, the present effort would be a significant step forward in the understanding of the fundamental theoretical origins of the Proca theory.
10) As will be demonstrated in a future reading, the present unified theory yields not only the Dirac equation, but the general spin Dirac equations in curved spacetime together with the fundamental theoretical origins of the Dirac equation as a condition for smoothness of the RHS. We consider this to be one of the most immediate and most outstanding achievements of the present theory. This we believe must give credence to the theory that, perhaps, it most certainly contains in it, a grain and an element of truth and is thus worthy of one’s valuable time to consider as a candidate unified theory.
16. Recommendations
Once again, assuming the correctness or acceptability of the ideas presented herein, we hereby put forward the following recommendations:
1) In-order to obtain the full quantized version of the present UFT, there is need to apply to it [present theory], the already available and well known methods of second quantization. This second quantization introduces the uncertainly principle into the theory. Certainly, this is what is needed for a full quantization of the theory. We are hopeful that this task will be taken up by others.
2) There is need to consider gravitomagnetism as a fully fledge science and not a first approximation of general relativity. We anticipate that such as approach must resolve some of the existing gravitational anomalies such that the secular drift of the Earth-Moon system [58] [59] from the Sun and the drift of the Moon from the Earth [60] [61] and as-well the observed flyby anomalies [62] [63] and even darkmatter [64] -[67] .
3) There is need to consider the RHS with in mind the task of putting it on a firm much more clear mathematical footing.
4) There is need to consider the geodesic equation to see what is meaning is with regard to electromagnetism, gravitation and quantum mechanics.
5) Finally, we can not at this point say what kind of picture the present UFT projects of the Universe, however, one thing appear clear, its picture seem to has signatures of the present world. There is thus need to put the theory on a much firmer footing by checking all the mathematics here laid down.
Acknowledgements
We are heftily grateful to the National University of Science & Technology (NUST)’s Research & Innovation Department and Research Board for their unremitting support rendered toward our research endeavours; of particular mention, Prof. Dr. P. Mundy, Dr. P. Makoni, Dr. D. J. Hlatywayo and Prof. Dr. Y. S. Naik’s unwavering support. We are grateful to the insights of Dr. William Straub―his insights have helped refine some portions of the present theory. This reading is dedicated to my mother Setmore Nyambuya and to the memory of my dearly missed departed father Nicholas Nyambuya (04.10.1947-23.09.1999).
NOTES
1Theories of Principle are theories not based on hypothesis but on a fundamental empirical discovery or fact(s). Propelled on a train of sound logic, the fundamental empirical discovery [or fact(s)] leads to the understanding of the general characteristics of natural processes and phenomenon. From this, mathematical models are then developed which separate the natural processes and phenomenon into theoretical-mathematical descriptions of physical and natural reality. Thus, by analytical means, the necessary conditions that have to be satisfied are deduced and as such, separate physical events must satisfy these conditions. If the theory is correct, experience should then match the conclusions [1] .
2Dr. Philp E. Gibbs is founder of the viXra-preprint server found at http://www.viXra.org.
![]()
3Like all other things, only time will tell if this approach is correct.
![]()
4In Equation (11) above, the term ![]() must be treated as a single object with one index
must be treated as a single object with one index![]() . This is what this object is. One can set
. This is what this object is. One can set![]() . The problem with this setting is that we need to have the objects,
. The problem with this setting is that we need to have the objects, ![]() and
and![]() , clearly visible in the equation.
, clearly visible in the equation.
![]()
5By flat, it here is not meant that the spacetime is Minkowski flat, but that the metric has no off diagonal terms. On the same footing, by positively curved spacetime, it meant that metric has positive off diagonal terms and likewise, a negatively curved spacetime, it meant that metric has negative off diagonal terms.
![]()
6It must be understood here that the term “God” is here used in as a metaphor to mean a force, or agent that caused the Universe to come into existence and not the religious God of Father Abraham. Yes―in the serene and pristine of our privacy; we practically and wholesomely believe in the Christian God, the God of Father Abraham, but for scientific purposes, we feel there is no need to enter into endless debates on the nature of God, as this is beyond the realm science. Ours is merely to investigate the marvellous structure of World as it reveals itself by itself. A wise mind will know Who to attribute the beauty it discovers about the Universe.
![]()
7Professor Baez, J., General Relativity Tutorial-Parallel Transport: http://math.ucr.edu/home/baez/gr/parallel.transport.html. Accessed on this May 28, 2009.
![]()
8Here, we must hasten to say that we have not exactly derived the material tensor field![]() , but merely justified its physical existence on the fundamental basis of the need for tensorial affinities. Thus, this material field is not only justifiable on a fundamental physical level but, very much a part and parcel of the whole edifice of the marvellous structure of the spacetime continuum.
, but merely justified its physical existence on the fundamental basis of the need for tensorial affinities. Thus, this material field is not only justifiable on a fundamental physical level but, very much a part and parcel of the whole edifice of the marvellous structure of the spacetime continuum.
![]()
9In (115) below, the square ([*, *]) and curly ({*, *}) brackets are the usual commutator and anti-commutator brackets respectively.