Application of Principal Component Regression with Dummy Variable in Statistical Downscaling to Forecast Rainfall ()
1. Introduction
Climate change is the average change of one or more elements of weather in a particular area. One of the climate change phenomena in Indonesia is the change of rainfall amount at some places. The change will have a wide impact on various sectors, particularly the agricultural sector. The uncertain impact of climate change will affect the increase or decrease in agricultural production. Therefore, the estimation of rainfall gives a positive contribution to agriculture.
Rainfall is a common variable in research related to the impact of climate change. Rainfall estimation in Indonesia needs to develop the climate models with high resolution on a local-scale by considering global atmospheric circulation information such as global circulation model output (GCM) [1] . However, the information from GCM is still in global-scale and unavailiable for smaller scale phenomena. Techniques of statistical downscaling (SD) may be used to obtain local-scale climate information from GCM [2] . Generally, GCM data have large dimension and high correlation between the grid so that the common method in SD model is principal component regression (PCR) [1] .
SD modeling requires a strong relationship between rainfall and GCM precipitation data to describe the local climate variability well [3] . A strong relationship (high correlation) will produce a similar pattern between those data. However, the pattern of the GCM precipitation data was not the same as the pattern of rainfall data. There was time shift (time lag) on the GCM data. Therefore, determining the time lag is needed to be applied to GCM precipitation data. The time lag of GCM precipitation data can be determined by the highest cross-correlation between rainfall and GCM precipitation data calculated using the cross-correlation function (CCF).
SD technique with multirespon PLSR method had been used to forecast rainfall in Indramayu District [4] . Furthermore, PLSR, weighted least squares regression (WLSR), and PCR methods were also used to forecast rainfall in Sukadana weather station based on satellite data of tropical rainfall measuring mission (TRMM) [5] . In this research GCM data with time lag was used. Therefore, the objectives of the research were to determine the time lag of GCM data and build SD model using PCR method with time lag of the GCM precipitation data.
2. Material and Methods
2.1. Data
The data used in this research was GCM precipitation (mm/month) from climate model intercomparison project (CMIP5) as predictor variables and rainfall data (mm/month) in Indramayu district as response variable from 1979 to 2008. CMIP5 GCM data was downloaded from website http://www.climatexp.knmi.nl/ issued by the Netherlands KNMI.
The domain size of GCM used in this research was 8 × 8 square grid (2.5˚ × 2.5˚ for each grid) from 98.75˚E to 116.25˚E and from −16.25˚S to 1.25˚N above area of Indramayu. The size of domain 8 × 8 grids over the area of Indramayu showed that the estimate was more consistent and not sensitive to outliers [6] .
2.2. Methods
The steps of the analysis in this research were:
1) Determine the time lag of GCM data using CCF. If 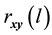 is cross-correlation between the
is cross-correlation between the 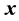 and
and 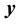 series at time lag-
series at time lag-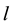 ,
, 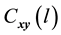 is covariance between
is covariance between 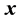 and
and 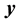 at time lag-
at time lag-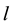 ,
, 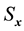 and
and 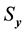 are the standard deviation of
are the standard deviation of 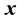 and
and 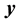 series respectively, the CCF can be formulated as Equation (1).
series respectively, the CCF can be formulated as Equation (1).
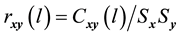 (1)
(1)
2) Identify multicollinearity precipitation data using variance inflation factors (VIF).
3) Apply SD technique using PCR method.
PCR method begins with principal component analysis (PCR) to produce new components that are not correlated with each other and referred to as the principal component (PC). The 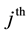 PC is given by Equation (2).
PC is given by Equation (2).
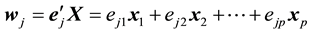 (2)
(2)
where 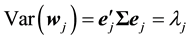 and
and![]() .
. ![]() and
and ![]() row are eigenvalue and eigen- vector of the variance covariance matrix
row are eigenvalue and eigen- vector of the variance covariance matrix![]() .
.
The general model of PCR can be formulated as Equation (3) [7] .
![]() (3)
(3)
Furthermore, the PCR model with ![]() component can be written as Equation (4).
component can be written as Equation (4).
![]() (4)
(4)
where ![]() is error vektor of size
is error vektor of size![]() ,
, ![]() is response variable vector of size
is response variable vector of size![]() ,
, ![]() is intercept,
is intercept, ![]() is vector that all element is one of size
is vector that all element is one of size![]() ,
, ![]() is PC matrix of size
is PC matrix of size![]() , and
, and ![]() is PC coefficient vector of size
is PC coefficient vector of size![]() . Estimator of regression coefficients using the least squares method can be formulated as Equation (5).
. Estimator of regression coefficients using the least squares method can be formulated as Equation (5).
![]() (5)
(5)
If errors of PCR model indicated that conditions were not homogeneous, then the dummy variables would be added to the PCR model. Dummy variables were determined by the result of grouping between the ![]() -score and
-score and ![]() -score. The plots between
-score. The plots between ![]() -scores and
-scores and ![]() -score were obtained from PLSR method.
-score were obtained from PLSR method.
If ![]() is a matrix of predictor variables, the PLSR method produces new components, which are called
is a matrix of predictor variables, the PLSR method produces new components, which are called ![]() -scores
-scores![]() . It is defined in Equation (6) with the
. It is defined in Equation (6) with the ![]() -weight coefficients are denoted by
-weight coefficients are denoted by ![]() [8] .
[8] .
![]() (6)
(6)
The ![]() -scores (
-scores (![]() ’s) have the following properties:
’s) have the following properties:
・ They are multiplied by the loadings![]() , so that the
, so that the ![]() -errors
-errors ![]() in Equation (7) are small.
in Equation (7) are small.
![]() (7)
(7)
・ The ![]() -scores are good predictor of
-scores are good predictor of ![]() with the weights
with the weights ![]() and errors
and errors ![]() in Equation (8).
in Equation (8).
![]() (8)
(8)
・ The ![]() -scores (
-scores (![]() ’s) were calculated using Equation (9).
’s) were calculated using Equation (9).
![]() (9)
(9)
4) Step 1-3 used data in period 1979-2007 and validation of the model used data period 2008.
3. Results and Discussion
3.1. Data Exploration
3.1.1. Time Lag of GCM Precipitation Data
Cross-correlation function was used to calculate the highest cross-correlation between the precipitation and rainfall data. The highest cross-correlation determined the time lag of GCM precipitation data. Based on Figure 1(a), the plot of rainfall in Indramayu showed that the highest average rainfall occurred in January and February, while the precipitation plots of ![]() showed in March (Figure 1(c)). Consequently the correlation between rainfall data and the precipitation data of
showed in March (Figure 1(c)). Consequently the correlation between rainfall data and the precipitation data of ![]() was low. Therefore, the CCF was used to determine the time lag of GCM precipitation data.
was low. Therefore, the CCF was used to determine the time lag of GCM precipitation data.
Figure 1(b) showed that precipitation ![]() had the highest cross-correlation (time lag) with rainfall data on the 2nd time lag. January rainfall occurred in March on the precipitation data
had the highest cross-correlation (time lag) with rainfall data on the 2nd time lag. January rainfall occurred in March on the precipitation data![]() . Therefore, the 2-month was lagged on the precipitation data
. Therefore, the 2-month was lagged on the precipitation data![]() . The results on Figure 1(d) showed that the scatter pattern of precipitation data
. The results on Figure 1(d) showed that the scatter pattern of precipitation data ![]() with time lag following the rainfall pattern so that could improve the correlation between rainfall data and the precipitation data of
with time lag following the rainfall pattern so that could improve the correlation between rainfall data and the precipitation data of![]() . In the same way, the time lag was also determined on the precipitation data from
. In the same way, the time lag was also determined on the precipitation data from ![]() to
to![]() . The farthest shift occurred at 10th time lag. However, the time lag of precipitation data generally occurred at first time lag.
. The farthest shift occurred at 10th time lag. However, the time lag of precipitation data generally occurred at first time lag.
The calculations showed that the time lag determination on GCM data might optimize the relationship between the precipitation and rainfall data. The number of GCM grid with lag (lag-GCM) which had a correlation larger than 0.7 with rainfall data was 73%. Meanwhile, the correlation between the rainfall and precipitation data without lag (GCM) larger than 0.7 only reached 9%.
3.1.2. Variance Inflation Factors
The calculations showed that the time lag determination on GCM data might optimize the relationship between the precipitation and rainfall data. The number of GCM grid with lag (lag-GCM) which had a correlation larger
than 0.7 with rainfall data was 73%. Meanwhile, the correlation between the rainfall and precipitation data without lag (GCM) larger than 0.7 only reached 9%.
3.2. Statistical Downscaling Model
3.2.1. Principal Component Regression
PCR is a method that can be used to overcome the problem of multicollinearity on predictor variables. Modeling using the PCR method begins with PCA to reduce the dimensions or to overcome the problems of multicollinearity. The number of PC used in the PCR model were selected based on the cumulative proportion of the total variability in the ranged from 65% to 95%. Table 1 showed that the PC1 on lag-GCM data was better in explaining data diversity than PC1 on GCM data. However, the next components on the lag-GCM data had a cumulative proportion which is relatively similar to the GCM data. The first 4 PC could explain 95% of the data variability. Thus, there were 4 PCR models based on the number of the PC that used, both the lag-GCM and GCM data.
The modeling results indicated the PCR model on lag-GCM data was better in explaining the data diversity than on data GCM (Table 2). The significant difference was shown by the model PC1R with ![]() values of 34.2% on GCM data and of 62% on lag-GCM data. This was caused by the proportion of PC1 variability on the GCM data was only 69%, while on the lag-GCM data was 83%. On average, PCR model on lag-GCM data had higher
values of 34.2% on GCM data and of 62% on lag-GCM data. This was caused by the proportion of PC1 variability on the GCM data was only 69%, while on the lag-GCM data was 83%. On average, PCR model on lag-GCM data had higher ![]() (ranged from 62% to 63%) than
(ranged from 62% to 63%) than ![]() (ranged from 34.2% to 62%) on GCM data. In addition, the root mean squared error (RMSE) value ranged from 66.67 to 67.33 on lag-GCM data and from 67.15 to 88.58 on GCM data. This indicated that the determination of time lag for the GCM precipitation data was able to increase the
(ranged from 34.2% to 62%) on GCM data. In addition, the root mean squared error (RMSE) value ranged from 66.67 to 67.33 on lag-GCM data and from 67.15 to 88.58 on GCM data. This indicated that the determination of time lag for the GCM precipitation data was able to increase the ![]() value around 9.7% and lowered RMSE value around 9.7.
value around 9.7% and lowered RMSE value around 9.7.
The error was analyzed on the PC1R model using GCM and lag-GCM data. Figure 2(a) and Figure 2(b) showed that the error scatter formed a divergent pattern. The higher fitted rainfall gave the bigger absolute value
![]()
Table 1. Eigenvalue and diversity proportion of 5 PCs for GCM and lag-GCM data.
![]()
Table 2. RMSE and R2 values of each model with GCM and lag-GCM data.
![]()
![]() (a) (b)
(a) (b)
Figure 2. Error plots of PC1R model with (a) GCM data and (b) lag-GCM data.
of errors. This case indicated heterogeneous in error. The condition of error heterogeneity also occurred in the PC2R, PC3R, and PC4R models on lag-GCM and GCM data. Therefore, the PCR models were modified by the addition of dummy variables.
(a) (b)
Figure 1 Error plots of PC1R model with (a) GCM data and (b) lag-GCM data
Dummy variables in the PCR models overcome the problems of error heterogeneity. Dummy variables were determined based on the result of grouping from PLSR method. Figure 3 showed the five groups of rainfall data based on dominant color group. The first group generally occurred from May to October with the intensity from 0 to 110.53 mm/month, the second group generally occurred in March, April, and November with the intensity from 110.54 to 235.07 mm/month, third group generally occurred in December withthe intensity from 235.08 to 353.73 mm/month, fourth group generally occurred in February with the intensity from 353.74 to 454.73 mm/month, and fifth group generally occurred in January withthe intensity more than 454.73 mm/month. This grouping was based on the discriminant analysis and a percentage of 94.8% clustering accuracy. Thus, the four dummy variables were added to the PCR models.
Table 3 showed the PCR models with dummy variables (PCRD) gave a better model than the PCR models without dummy variables. PCRD models gave ![]() ranged from 91.2% to 93% on GCM data and from 92.9% to 93.4% on lag-GCM data (Table 3). The addition of dummy variables in the PCR models increased the model performance to explain variability of rainfall around 39.68% on GCM data and around 30.53% on lag-GCM data. The RMSE values were relative small, ranged from 29.09 to 32.56 on GCM data and from 28.73 to 29.34 on lag-GCM data. But on average, PCRD models using lag-GCM data gave higher
ranged from 91.2% to 93% on GCM data and from 92.9% to 93.4% on lag-GCM data (Table 3). The addition of dummy variables in the PCR models increased the model performance to explain variability of rainfall around 39.68% on GCM data and around 30.53% on lag-GCM data. The RMSE values were relative small, ranged from 29.09 to 32.56 on GCM data and from 28.73 to 29.34 on lag-GCM data. But on average, PCRD models using lag-GCM data gave higher ![]() values (93.10%) than using the GCM data (92.55%).
values (93.10%) than using the GCM data (92.55%).
The error diagnosis of PC1RD model using GCM and lag-GCM data showed 5 groups of error (Figure 4(a) and Figure 4(b)). Grouping was caused by the addition of dummy variables in PCR models. However, the error scatter patterns of each group in Figure 4(a) and Figure 4(b) were more homogeneous than the error scatter pattern in the PCR models. The conditions of homogeneous in error were also indicated by the PC2RD, PC3RD, and PC4RD models on GCM and lag-GCM data. It meant, the addition of dummy variables in the PCR models gave model that was more homogeneous in error than the PCR models without dummy variables.
3.2.3. Model Validation and Selection
Model validation stage based on the root mean squared error of prediction (RMSEP) and correlation values between actual rainfall and estimated rainfall using GCM and lag-GCM data. Based on Table 4, the estimated rainfall data using lag-GCM was better than using the GCM data. The estimated value of PCR models on lag-GCM had higher correlation (ranged from 0.88 to 0.91) and lower RMSEP (ranged from 71.91 to 77.29) than correlation (ranged from 79.93 to 103.74) and RMSEP (84.22) of PCR models on GCM data. In addition, the PCRD models gave estimator for rainfall with RMSEP ranged from 28.48 to 31.04 on lag-GCM data and RMSEP ranged from 31.51 to 35.06 on GCM data, the correlation ranged of 0.99 and from 0.97 to 0.98 respectively. Generally, the PCRD model that involving PC1 on lag-GCM gave the best estimated model for rainfall that had the smallest RMSEP (28.48) and correlation 0.99.
![]()
Table 3. RMSE and R2 values of each model with GCM and lag-GCM data.
![]()
![]() (a) (b)
(a) (b)
Figure 4. Error plots of PC1RD model with (a) GCM and (b) lag-GCM data.
![]()
Table 4. RMSEP and correlation values of each model with lag-GCM and GCM data.
Figure 5(a) and Figure 5(b) showed that the results of estimated rainfall were lower than the actual rainfall from January to March. However, the estimators were higher than the actual rainfall from April to December. PCR models on lag-GCM data could estimate rainfall data that follows the actual rainfall patterns, particularly from June to December. In addition, the estimator using lag-GCM data was closer to actual value (Figure 5(a)). However, the estimator using GCM data was not following the actual rainfall patterns, especially PC1R model (Figure 5(b)). The distance between the estimated and the actual values was quite distant. Similar to the PCR models, PCRD models using data lag-GCM also showed better performance than using the GCM data (Figure 6(a) and Figure 6(b)). On average, the distance between the actual and the estimated values of PCRD models using data lag-GCM were closer than using the GCM data (Figure 6(a)). This meant that the determination of time lag for the GCM precipitation data gave estimator more accurate in the SD model than GCM data without it.
Figure 6 showed that the PCRD models captured the better rainfall pattern than PCR models (Figure 5). PCRD models were more accurate in estimating rainfall, particularly at high intensity rainfall (from January to March). The distance between the actual and the estimated values of PCRD models were relatively closer than the estimated from PCR models. Figure 5 showed that the PCR model failed estimating rainfall from January to March. It indicated that addition of dummy variables in the PCR models could fix the estimated rainfall. But on average, PCRD model using lag-GCM data were more accurate in giving the estimated rainfall than PCR model.
![]()
![]() (a) (b)
(a) (b)
Figure 5. Estimated rainfall plot of PCR models with (a) lag-GCM and (b) GCM data.
![]()
![]() (a) (b)
(a) (b)
Figure 6. Estimated rainfall plot of PCRD models with (a) lag-GCM and (b) GCM data.
4. Conclusion
Cross-correlation between rainfall and GCM precipitation data has an important role in modeling of statistical downscaling. The highest cross-correlation determined the time lag that optimized the relationship between rainfall data and the data of GCM precipitation, so it improved the accuracy prediction of rainfall data. Estimation of rainfall using the GCM precipitation data with time lag was more accurate than using GCM precipitation data without time lag. The PCR models with dummy variables and using GCM precipitation data with time lag gave better estimated rainfall than PCR models without dummy variables. The model involving one principal component was the best model that had high correlation (0.99) and the smallest RMSEP (28.84).
NOTES
*Corresponding author.