1. Introduction
Optimal control theory, which is an extension of calculus of variations is a mathematical optimization method for deriving control policies. In essence, an optimal control is set of differential equations describing the path of the control variables that minimize the cost functional. Mond and Hanson [1] were the first to formulate a control problem as a mathematical programming problem and studied Wolfe type duality for the same under convexity of the function involved in the formulation. Subsequently a number of duality results for a control problem involving differentiable functions were obtained, for example, in the references [2] -[5] . There exist applications of optimal control with nondifferentiable terms which appear in the problem of friction. This motivated Chandra et al. [2] to study optimality and duality for a class of nondifferentiable control problem containing the square root of certain quadratic form in the integrand of the objective functional. The popularity of this type of mathematical programming problem seems to originate from the fact that even though the objective functions and/or constraint functions are nonsmooth, a simple representation for the dual may be found. Non smooth mathematical programming theory deals with much more general functions by means of generalized subdifferential [6] and quasidifferential [7] . However, the square root of a positive semidefinite quadratic form and support function are of the few cases of a nondifferentiable function for which subdifferentials can explicitly be written.
In this research we introduce a control problem with a support function in the integrand of the objective functional and each inequality constraint function. Optimality conditions for this nondifferentiable control problem are derived and Wolfe type duality is investigated under pseudoconvexity. Special cases are generated. The linkage between our results and those of nonlinear programming problem containing support function is also indicated.
2. Control Problem and Preliminaries
We introduce the following control problem involving support functions:
(CP): Minimize: 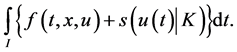
Subject to
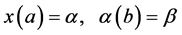 (1)
(1)
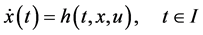 (2)
(2)
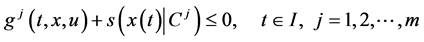 (3)
(3)
where
1) 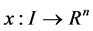 is a differentiable state vector function with its derivative
is a differentiable state vector function with its derivative 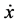 and
and 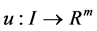 is a smooth control vector function.
is a smooth control vector function.
2) 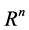 denotes an
denotes an 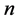 -dimensional Euclidean space and
-dimensional Euclidean space and 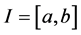 is a real interval, and
is a real interval, and
3)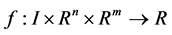 ,
, 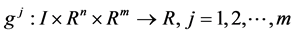 and
and 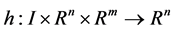 are continuously differentiable.
are continuously differentiable.
4) 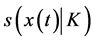 and
and 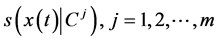 are the support function of the compact set
are the support function of the compact set 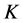 and
and ![]() respectively.
respectively.
Denote the partial derivatives of ![]() by
by![]() ,
, ![]() and
and![]() ,
,
![]()
where superscript denote the vector components. Further ![]() represents the space of continuously differentiable
represents the space of continuously differentiable
state functions ![]() such that
such that ![]() and
and ![]() and is equipped with the norm
and is equipped with the norm![]() , and
, and![]() , the space of piecewise continuous control vector functions
, the space of piecewise continuous control vector functions ![]() having the uniform norm
having the uniform norm![]() . The differential Equation (2) with initial conditions expressed as
. The differential Equation (2) with initial conditions expressed as ![]()
![]() may
may
be written as![]() , where
, where ![]() being the space of continuous function from
being the space of continuous function from ![]() to
to ![]() defined as
defined as![]() . In the derivation of these optimality condition, some constraint qualification to make the equality constraint locally solvable [2] is needed for this and hence, the Fréchet derivative of
. In the derivation of these optimality condition, some constraint qualification to make the equality constraint locally solvable [2] is needed for this and hence, the Fréchet derivative of![]() , (say) with respect to
, (say) with respect to![]() , namely
, namely
![]() are required to be subjective. We review some well known facts about a support function for easy reference. Let
are required to be subjective. We review some well known facts about a support function for easy reference. Let ![]() be a compact convex set in
be a compact convex set in![]() . Then the support function
. Then the support function
of ![]() denoted by
denoted by ![]() is defined as,
is defined as, ![]()
A support function, being convex and everywhere finite, has a subdifferential in the sense of convex analysis, that is, there exists ![]() such that
such that ![]() for all
for all ![]()
As in [8] the subdifferential of ![]() is given by
is given by![]() . Let
. Let ![]() be normal cone at a point
be normal cone at a point![]() . Then
. Then ![]() if and only if
if and only if ![]() or equivalently,
or equivalently, ![]() is in the subdifferential of
is in the subdifferential of ![]() at
at ![]()
3. Optimality Conditions
In this section, we derive necessary optimality conditions of both Fritz John and Karush-Kuhn-Tucker type for the control problem (CP) stated in the preceding section.
Theorem 1. (Fritz John Conditions): If ![]() is an optimal solution of (CP) and the Fréchet derivative
is an optimal solution of (CP) and the Fréchet derivative ![]() is surjective, then there exist Langrange multipliers
is surjective, then there exist Langrange multipliers ![]() and piecewise smooth
and piecewise smooth ![]() and
and ![]() such that
such that
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
Proof: The problem (CP) may be expressed in its abstract version as
(ECD): ![]()
subject to
![]()
where ![]()
![]() is given by
is given by![]() ,
, ![]() and
and![]() ; the nonnegative orthant of
; the nonnegative orthant of ![]()
By the result of [9] it follows that there exist Langrange multipliers ![]() (the dual of
(the dual of![]() ) and
) and ![]() in the dual space of
in the dual space of ![]() satisfying
satisfying
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
The condition (12) reduces to
![]() (16)
(16)
![]() (17)
(17)
Since ![]() is continuously differentiable function of
is continuously differentiable function of ![]() and
and![]() ,
, ![]() is Fréchet differentiable with respect to
is Fréchet differentiable with respect to![]() . The partial derivatives of
. The partial derivatives of ![]() with respect to
with respect to ![]() and
and![]() , denoted by
, denoted by ![]() and
and ![]() respectively, are given by
respectively, are given by
![]() (18)
(18)
![]() (19)
(19)
Similar results for ![]() and
and ![]() as for
as for ![]() can be given. Assume now subject to later validation that,
can be given. Assume now subject to later validation that, ![]() can be represented by measurable function
can be represented by measurable function ![]() with
with ![]() satisfying
satisfying
![]() (20)
(20)
Define the convex function ![]() by
by![]() . From [2] its subdifferential,
. From [2] its subdifferential,
![]()
Now![]() . From ([6] , Theorem 3), we have
. From ([6] , Theorem 3), we have
![]() (21)
(21)
with ![]() measurable, namely
measurable, namely ![]() from (16).
from (16).
Let![]() , where
, where ![]() denotes the vector support function whose
denotes the vector support function whose ![]() component is
component is![]() . Then
. Then
![]() (22)
(22)
Denoted by ![]() the Clarke generalized gradient [6] with respect to
the Clarke generalized gradient [6] with respect to![]() . Then
. Then
![]() (23)
(23)
The above is possible by using the representation of ![]() as the convex hull of limit of points of gradients at smooth points near
as the convex hull of limit of points of gradients at smooth points near![]() . Here
. Here ![]() denotes the algebraic sum of sets. Since
denotes the algebraic sum of sets. Since ![]() is convex, we have for each
is convex, we have for each ![]()
![]() (24)
(24)
From [10] , it implies that ![]() if and only if these exists a measurable function
if and only if these exists a measurable function ![]() such that
such that
![]()
Now
![]() (25)
(25)
Consider,
![]() (26)
(26)
Using (18), (25), (26), we have
![]() (27)
(27)
Since the integral values for any![]() , by Lemma 2 ([11] , p. 500), it follows that
, by Lemma 2 ([11] , p. 500), it follows that
![]() (28)
(28)
The cited lemma assumes that the expression in the square bracket of (27) is piecewise continuous, but this readily extends to measurable. This validates (4). On the basis of analysis needed to validate (28), we can easily establish
![]()
Also ![]() along with
along with ![]() of (24) yields
of (24) yields
![]()
By the application of the above-cited lemma, this gives (6) i.e.
![]()
The remaining proof of the theorem easily follow on the lines of the proof of Theorem 4.1 of [2] .
Hence the above analysis established the theorem fully.
Chandra et al. [2] pointed out if the optimal solution for (CP) is normal, then the Fritz John type optimal conditions reduce to the following Karush-Kuhn-Tucker optimal conditions:
Theorem 2: If ![]() is an optimal solution and is normal and
is an optimal solution and is normal and ![]() is surjective, there exist piecewise smooth
is surjective, there exist piecewise smooth![]() ,
, ![]() with
with![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]()
Such that
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
4. Wolfe Type Duality
We propose the following dual as the Wolfe type dual and validate duality results amongst (CP) and (WCD).
(WCD): Maximize
![]()
subject to
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
Theorem 3 (Weak Duality): Assume that
1) ![]() is feasibility for (CP)
is feasibility for (CP)
2) ![]() is feasible for (CD) and
is feasible for (CD) and
3) for all feasible, ![]()
![]()
is pseudo convex in ![]() for all
for all ![]() and
and![]() ,
, ![]()
Then
![]()
Proof: Combining (37) and (38), we have
![]()
By the pseudoconvexity hypothesis 3), this yields
![]() (41)
(41)
Since ![]() is feasible for (CP), we have
is feasible for (CP), we have
![]() ,
,
implying
![]() ,
,
and
![]() ,
,
implying
![]()
Since![]() ,
, ![]() , we have
, we have
![]()
From (41), we have
![]()
This implies
![]()
That is,
![]()
Theorem 4 (Strong duality): If ![]() is an optimal solution of (CP) and is normal, there exist piecewise smooth
is an optimal solution of (CP) and is normal, there exist piecewise smooth ![]() where
where![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() such that
such that ![]() is feasible for (WCD) and the optimal values of the problem (CP) and (WCD) are equal. If also the hypotheses of Theorem1 hold, then
is feasible for (WCD) and the optimal values of the problem (CP) and (WCD) are equal. If also the hypotheses of Theorem1 hold, then ![]() is an optimal solution of the problem (WCD).
is an optimal solution of the problem (WCD).
Proof: Since ![]() is an optimal solution of (CP) and is normal, by Theorem 1, it implies that there exist piecewise smooth
is an optimal solution of (CP) and is normal, by Theorem 1, it implies that there exist piecewise smooth![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]()
![]() such that conditions (4)-(10) of the theorem are satisfied. The conditions (4)-(6) together with (9) and (10) imply the feasibility of
such that conditions (4)-(10) of the theorem are satisfied. The conditions (4)-(6) together with (9) and (10) imply the feasibility of ![]() for (WCD). The condition (6)-(8) yield the equality of objective functionals of the two problem. In view of this equality and the hypotheses of Theorem 3, the optimality of
for (WCD). The condition (6)-(8) yield the equality of objective functionals of the two problem. In view of this equality and the hypotheses of Theorem 3, the optimality of ![]() for (WCD) is obtained.
for (WCD) is obtained.
Theorem 5: (Strict Converse Duality): Assume
(H1): ![]() is an optimal solution and is normal;
is an optimal solution and is normal;
(H2): ![]() is an optimal solution;
is an optimal solution;
(H3): ![]() is strictly pseudo convex.
is strictly pseudo convex.
then![]() , i.e.
, i.e. ![]() is an optimal solution of (CP).
is an optimal solution of (CP).
Proof: Assume that![]() . By Theorem 4, there exist piecewise smooth
. By Theorem 4, there exist piecewise smooth ![]() with,
with, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() ,
, ![]() such that
such that![]() is an optimal to (CD) and
is an optimal to (CD) and
![]()
From the feasibility of ![]() for (WCD), we have
for (WCD), we have
![]()
This by strict pseudoconvexity hypothesis (H3) yields,
![]()
Since![]() , and
, and![]() , this yields,
, this yields,
![]()
This is absurd. Hence ![]() is an optimal solution of (CP).
is an optimal solution of (CP).
5. Converse Duality
The problem (WCD) can be written as the follows:
Maximize: ![]()
Subject to ![]()
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
Consider ![]() and
and ![]() as defining a map-
as defining a map-
pings ![]() and
and ![]() respectively where
respectively where ![]() is the space of piecewise smooth
is the space of piecewise smooth![]() ,
, ![]() is space of piecewise smooth
is space of piecewise smooth![]() ,
, ![]() is the space of piecewise of smooth
is the space of piecewise of smooth![]() ,
, ![]() ,
, ![]() and
and ![]() are Banach spaces.
are Banach spaces. ![]() and
and
![]() with
with![]() . Here some restrictions are required on the equality constraints. For this it suffices that if the Fréchet derivatives
. Here some restrictions are required on the equality constraints. For this it suffices that if the Fréchet derivatives
![]()
and
![]()
have weak ![]() closed range.
closed range.
Theorem 6. (Converse Duality): Assume
(A1):![]() ,
, ![]() and
and ![]() are twice continuously differentiable.
are twice continuously differentiable.
(A2): ![]() is an optimal solution of (CP).
is an optimal solution of (CP).
(A3): ![]() and
and ![]() have weak
have weak ![]() closed range.
closed range.
(A4): The matrix ![]() is nonsingular.
is nonsingular.
Then ![]() is an optimal solution of (CP) and the optimal values of (CP) and (WCD) are equal.
is an optimal solution of (CP) and the optimal values of (CP) and (WCD) are equal.
Proof: Since ![]() is an optimal solution of (WCD), by Theorem 1 there exists
is an optimal solution of (WCD), by Theorem 1 there exists![]() ,
,
and piecewise smooth functions![]() ,
, ![]() , and
, and ![]() such that
such that
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
![]() (46)
(46)
![]() (47)
(47)
![]() (48)
(48)
![]() (49)
(49)
![]() (50)
(50)
Using (36) and (37) in (42) and (43) respectively, we obtain
![]()
The equations can be combined in the matrix form as,
![]()
This, due to the hypothesis (A4) yields
![]() (51)
(51)
Let![]() , then (44) implies
, then (44) implies![]() ,
, ![]() , consequently we get
, consequently we get ![]() contradicting (50), hence
contradicting (50), hence ![]()
The relations (44) together with (48) and (45) respectively imply
![]() (52)
(52)
![]() (53)
(53)
From (52) and![]() ,
, ![]() , we have
, we have
![]() (54)
(54)
From (53) along with![]() ,
, ![]() , we obtain
, we obtain
![]() (55)
(55)
In view of (51) and definition of a normal cone (50) and (51), we have![]() ,
, ![]() ,
, ![]() and
and ![]() implying
implying
![]() ,
,
and
![]() (56)
(56)
From (52) together with (56) and
![]() ,
,![]() ,
, ![]() (57)
(57)
imply
![]() (58)
(58)
From (53) and (57), the feasibility of ![]() for (CP) follows.
for (CP) follows.
Consider
![]()
(by using (54), (55) and (56).
This implies that the values of objective functionals of the problem are equal. Consequently in view of the hypothesis of Theorem 1 it implies that ![]() is an optimal solution of (CP).
is an optimal solution of (CP).
6. Special Cases
Let for![]() .
. ![]() and
and![]() ,
, ![]() be positive semidefinite matrics and continuous on
be positive semidefinite matrics and continuous on![]() . Then
. Then
![]()
where
![]()
and
![]()
where
![]()
The control problems of the preceding section becomes as the following:
(WCD0): Maximize
![]()
Subject to
![]()
![]()
![]()
![]()
![]()
If![]() ,
, ![]() are deleted and
are deleted and ![]() is replaced by
is replaced by![]() , the problem (CP0) and (WCD0) reduce to those studied by Chandra et al. [2] .
, the problem (CP0) and (WCD0) reduce to those studied by Chandra et al. [2] .
7. Related Nonlinear Programming Problems
If the functions appearing (CP) and (WCD) are independent, of ![]() then these problems reduce to the following nonlinear programming problem with support functions not reported explicitly in the literature.
then these problems reduce to the following nonlinear programming problem with support functions not reported explicitly in the literature.
(CP0): Minimize ![]()
subject to ![]()
(WCD0): Maximize ![]()
subject to ![]()
![]()
![]()
![]()
If ![]() and
and ![]() are replaced by
are replaced by ![]() and
and ![]() respectively, the above problem reduce to the following problem studied by Husain et al. [12] .
respectively, the above problem reduce to the following problem studied by Husain et al. [12] .
(NP1): Minimize ![]()
Subject to ![]()
(WNP1): Maximize ![]()
Subject to ![]()
![]()
![]()
8. Conclusion
Fritz John and Karush-Kuhn-Tucker type necessary optimality conditions for class of nondifferentiable control problems are derived. As an application of Karush-Kuhn-Tucker type necessary optimality conditions, Wolfe type dual is formulated and various duality theorems under generalized convexity conditions are proved. The linkage between our duality results and those of a nonlinear programming problem with support functions is indicated.