An Improved Finite Temperature Lanczos Method and Its Application to the Spin-1/2 Heisenberg Model on the Kagome Lattice ()
1. Introduction
Study about the spin-1/2 Heisenberg model on the kagome lattice [1] -[4] has remained to be formidable during several decades. Recently this model has been studied extensively to pursue a possible candidate for a quantum spin liquid [5] -[10] . Also as a spin-1/2 antiferromagnet with the kagome geometry, Kapellasite,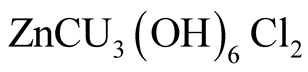 
has been synthesized and has been studied about its magnetic properties [11] . These experimental works require theoretical studies on this system at finite temperature
. One of these studies is made by the high-temperature series expansion that has shown the quite stable results for the uniform susceptibility over the wide range of temperature [12] -[14] . But this study has failed to present conclusive results for the specific heat at low
. Reasons of this failure are that this method such as the high-temperature series expansion is difficult at low
, and that the specific heat of the model on the kagome lattice cannot be described by the power-law behavior at low
. Also we should realize that this method explains only a half of the entropy.
In this work, we will present calculations of the specific heat at low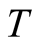 
by the exact approach for small clusters. The exact approach is very powerful and extensively applied for study at zero 
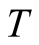[15] -[17] , although the size is severely limited. There are few researches on the exact approach to calculations of the specific heat at finite
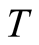. Only some results on 
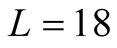or 
clusters are found in [12] [13] . Here L is the total number of sites. By these previous works, it is understood that ordinary calculations on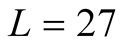 
or larger lattices are quite difficult because the system on the kagome lattice has the complicated structure at low
. We point out the Chebyshev polynomial expansion (CPE) as one method of the exact approaches at finite 
[18] [19] . Another method is the finite temperature Lanczos method (FTLM) [20] [21] .While the polymial expansion method is well mathematically understood, in the FTLM we should be careful to control numerical errors. Due to this weakness there are a fewer applications of the FTLM, compared with the CPE [18] , although both methods give us the same calculation costs.
However, recently the FTLM has been improved by making use of the full irreducible representation of the symmetry group [22] , by applying the method to the microcanonical ensemble [23] or by combining it with the meanfield approach [24] . Also the improvement has been made by modifying the initial state for the Lanczos method [25] . As a result, we can make precise calculations of thermodynamic quantities of strongly correlated systems [22] . Also it has been applied to the Kondo lattice [26] , and J1-J2 Heisenberg model [27] .
Here we would like to emphasize an advantage of the FTLM that we calculate the specific heat at many values of 
without keeping states in the computer memory. This is quite important in study by limited resources of computers.
In calculations at low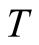
, we need the large number 
of iterations for obtaining the orthogonal states in the FTLM. In calculations of
, we have to worry about errors on the orthogonality of the states. In order to keep that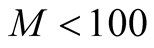
, we propose a two-step method, which is some extension of the method, in which the initial state for the Lanczos method is modified [25] .
In the first step, we use the CPE to generate a state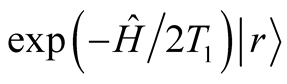 
at moderate
. Here 
is a random vector. In the second step, we employ the FTLM. We call our proposed method as a two-step finite temperature Lanczos method (tFTLM).
In addition to this two-step strategy, we propose a sampling method for selecting the initial random state. It is well known that the random vector method is quite effective for the trace calculation of the partition function. If the Hamiltonian has some symmetry, the basis states are divided into symmetry sectors. In each symmetry sector we calculate the partition function. At the infinitely high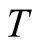 
a sampling weight of each symmetry sector is proportional to the number of basis states in the symmetry sector. But at very low
, the partition function depends extremely on the lowest energy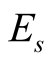 
of the symmetry sector
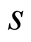. Based on this consideration, we use a product of 
and the number of basis states for a sample weight of a sector.
Contents of this paper are as following. After a brief review on the FTLM, we propose our method in section 2. In section 3, we make an examination about our method in order to show that the tFTLM is effective at very low
. After the examination, we apply the tFTLM to calculate the specific heat of the spin-1/2 Heisenberg model on the kagome lattice. By results of 
and 
lattice we conclude that the specific heat shows the curve of the shoulder around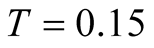
. A final section is devoted to a conclusion.
2. Two-Step Finite Temperature Lanczos Method
First we present a brief description on the FTLM. We consider calculations of a static expectation value of an operator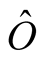 
at
.
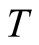(1)
with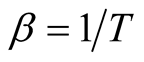 
and a sum over a complete orthonormal basis set
. Here N is the dimension of the vector space. Using the FTLM it is approximated by
(2)
(3)
with a sum over symmetry sectors s of dimension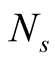
. The trace in (1) is replaced by the sum over 
s random vectors 
in (2) and (3) [28] [29] . 
is the number of iterations in the Lanczos procedure. On each random vector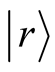
, the Lanczos procedure gives us the eigenenergies 
and their corresponding eigenvectors
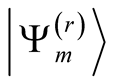, whose number is
. Because we adopt the random vector method, the calculation cost is of order of
.
The accuracy of the FTLM depends on obtained eigenvalues in the Lanczos method. When a system size becomes large, we need a quite large number 
in order to obtain the eigenvalue that is equal or nearly equal to the lowest energy of the system. However, 
could not be large, because in the Lanczos method the error on the orthogonality becomes large as 
is large. The maximum value of 
is about 100 [18] . The limit of 
gives us the minimum 
where calculations are reliable.
This limitation can be avoided in the Lanczos method for the energy calculation at zero 
by repeating this method several times. In order to introduce this repetition into the FTLM, we propose a two-step method. In the first step we generate a state 
at moderate
.
, (4)
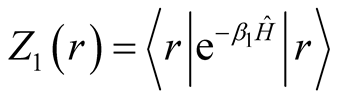. (5)
For this calculations of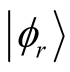
, we use the CPE.
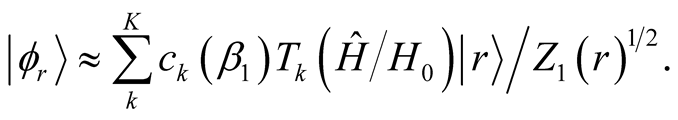(6)
Here 
is the k-th Chebyshev polynomial. Here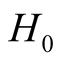 
is determined in order that the absolute value of 
is less than 1.
The precision of the approximation in the first step calculation can be controlled by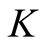
. We would like to reduce the numerical error of the state 
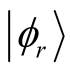to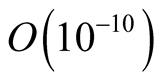
, so that 
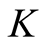is fixed by the value of
.
Next we carry out the second step procedure. Here we apply the Lanczos method, where we use this state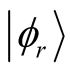 
as the initial state.
(7)
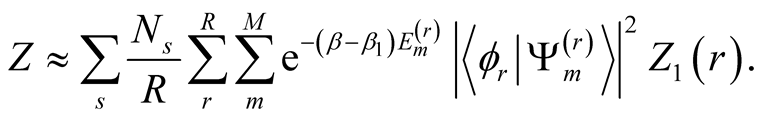(8)
In the Lanczos procedure we obtain eigenenergies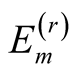 
and their corresponding eigenvectors
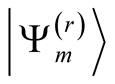, whose number is
.
Finally we describe a sampling method for selecting the initial random state. As described in the introduction, at low 
the partition function depends extremely on the lowest energy 
of the symmetry sector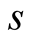
. If 
differs from each other, it is not effective that only the number of basis states 
of the symmetry sector is used as the sampling weight. The Heisenberg model on the kagome is a typical example of cases that there are some differences between
’s. For our calculations we use the product of 
and the number of basis states for the sample weight of a sector. Therefore a probability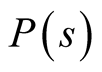 
of selecting s is given by
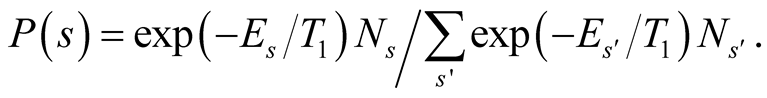
Using this probability
, we obtain
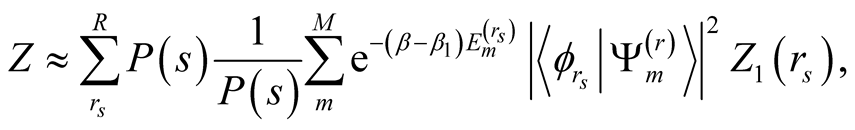(9)
The following is a procedure for sampling. First we select s according to the probability
. Next we generate a random vector in the selected s. We apply the tFTLM to calculate the partition function. After that we multiply this partition function by the factor of
.
3. The Specific Heat
First we make an examination about our method by applying the tFTLM to calculations in the spin-1/2 Heisenberg model on the kagome lattice. The Hamiltonian of this model is defined by
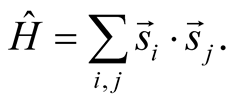
Here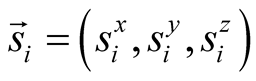 
is a spin operator of the spin one-half at a site
. The sum is carried out over a pair of sites on a link of the kagome lattice.
For the examination of the tFTLM we calculate the specific heat on the kagome antiferromagnet of the 
lattice. Although the exact results on it cannot be available, the specific heat per site 
must be quite small at extremely low 
on the finite lattice. In Figure 1, we plot the specific heat until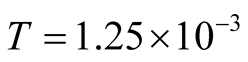
. The calculations are made using the FTLM and the tFTLM. The specific heat obtained by the FTLM of 
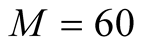does not fall to the zero, but remains constant. Results by the FTLM of 
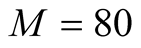have the same tendency, though the constant value becomes small. About results by the tFTLM, the specific heat has fallen to the value that is consistent with zero. This figure shows that the tFTLM can be applied safely to the extremely low
.
Next we make calculations of the 
of the spin-1/2 Heisenberg model on the kagome lattice. Here we give a description about parameters of the tFHTM on 
and
. In the first step we have two parameters of 
and
. 
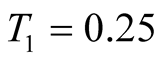is chosen in order to check our method, by comparing our results with results of the FTLM or of the high-temperature series expansion [12] . In order to reduce the calculation error into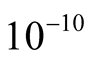 
about a given random vector, we need a ratio of coefficients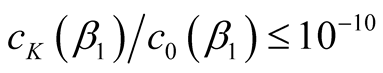 
in the Chebyshev polynomial (6). For obtaining this ratio, we determine 
in (6). In the second step the minimum value of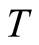
, at which calculations are made, is 0.0125 for making valuable discussions on the size dependence of the specific heat. For determining a value of
, we check the reliability of calculations using only one random vector. After this examination we fix that
.
Our results on clusters of 
are given in Figure 2. From the study by the high-temperature series expansion analysis [12] [13] we can say that the dependence of the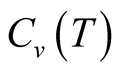 
at 
or at the higher 
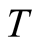on the size is quite small. Our results support this little dependence on the cluster size. On data at 
we find the dependence of the specific heat 
on the cluster size, but it is small. By this small dependence, we can say that the curve of the 
on the temperature has changed from the curve at
. As the study of [12] [13] showed, the high-temperature series expansion could not explain this curve at this temperature. On the entropy 
that is calculated by the integration from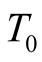 
to the infinitely high
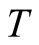we have that
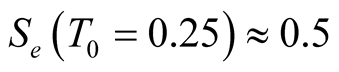. This small value suggests existence of the huge number of excited stateswhose gap energies are small than
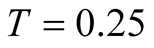. At
, we can find the large dependence of the 
on the cluster size. Therefore we could not mention a quantitative statement on the curve of the specific heat.
But at 
we can make a qualitative discussion. We find the qualitatively same results on data of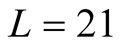 
and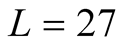
, which show the shoulder of the 
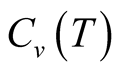curve. The 
on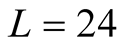 
shows the clear peak. This fact gives us the qualitative difference between the 
on the even size lattice and that of the odd size lattice. On the 
lattice, the peak of the 
curve is not found, and only the shoulder is seen. This tendency suggests that the curve of the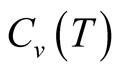 
on the larger even size lattice will agree with the curve on
. Summarizing our calculations, they show that this shoulder survives at the large 
limit at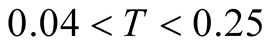
.
4. Conclusions
In this work, we presented two improvements on the FTLM in order to apply this method to systems at very low
Figure 1. The specific heat at low temperature on the kagome lattice of 
In the tFTHM,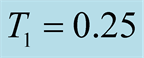
. The number of sampling random vectors is 1000.
temperature. One improvement was to introduce the two-step FTLM, tFTLM. In the first step we used the Chebyshev polynomial expansion to calculate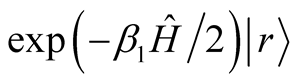 
at moderate temperature
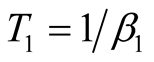. In the second step, we applied the FTLM using the calculated state as the initial state. By this two-step method, we don’t have to worry about the error of the Lanczos method. The following is a reason for this improvement. We need a large number of iterations on the Lanczos method at low temperature. This number is limited by the numerical error. While in the Chebyshev polynomial expansion this error is under the control. Therefore the numerical error can be quite small at the first step calculation. By the first step calculation we can reduce the number of the iteration of the Lanczos method in the second calculation.
Another improvement was to employ the effective sampling method for selecting a random vector. Using this sampling we can improve the efficiency of calculations. By the tFTLM, we calculated the specific heat of the spin-1/2 Heisenberg model on the kagome lattice of 30 sites. Our results confirmed the little dependence of the specific heat on the cluster size at
. At 
the dependence on the cluster size was small, so that we concluded that the curve of the specific heat changed from the curve at the higher temperature. Also our calculation suggested that the shoulder of the curve survived at the large cluster size at
. Summarizing this work, we proposed the tFTLM that was quite effective for numerical study at extremely low temperature and we presented definite results about the specific heat of the Heisenberg model on the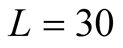 
kagome lattice.
We would like to make comments on further applications of the method. In this paper we applied the tFTLM to only static quantities at finite
. But it is easy to apply our method to the dynamical quantities. In study of the spin liquid model on the kagome, the work [7] has discussed the dynamical susceptibility that can be observed by neutron scattering and NMR. Also in numerical studies this is an issue to be examined, if we realize that around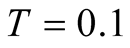 
results of the specific heat on 
differ from results on
, while the uniform susceptibility has showed the little dependence. Therefore it is very interesting to examine a size dependence of the dynamical susceptibility.
Also we comment on implication of our results of the specific heat. They require the more careful study on the spin liquid model, which suggests the power law behavior of the specific heat at low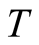
. The size dependence has become small around 
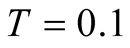in our results. Therefore we need a consistent description about our results and about the power-law behavior of the specific heat. But this is not easy as discussed in [12] . Our study suggests that the unified understanding of the specific heat is one of important issues on the Heisenberg model on the kagome lattice.
Acknowledgements
M. T. thanks Dr. Yasuko Munehisa for every encouragement on my study.