Studies of Electron Energy Distribution Function (EEDF) in Lithium Vapor Excitation at 2S→3D Two-Photon Resonance ()
1. Introduction
Generation of plasma in gases by intense laser pulses is a well-known optical phenomenon. The efficiency of this process can be increased by many orders of magnitude when the laser wavelength corresponds to an absorption line of ionized medium [1] . Laser-produced plasma sources are currently being developed to generate photons at a 13.5 nm wavelength to continue the development of faster computer chips. Utilizing the smallest wavelength for extreme ultraviolet lithography projection is the path to future progress in semiconductor technology [2] .
On one hand, the electron energy distribution function is a topic of continuing interest to the plasma physics, fusion, and astrophysical communities because they can play an important role in the formation, evolution, and radiative properties of a wide variety of plasma sources. Non-Maxwellian electron energy distributions have been predicted or detected in diverse laboratory sources including tokomaks [3] [4] , laser plasmas [5] - [7] and pulsed-power plasmas [8] - [10] as well as in astrophysical sources such as solar flares [11] [12] and active galactic nuclei [13] , where they are generated by strong electric fields or resonant laser-plasma interactions. On the other hand, measurements of the EEDF are important for many applications, such as studies of absolute negative conductivity in photo plasma. This effect was predicted in the medium of a Li+Ar+N2 mixture under optical resonant excitation of the 2s→2p transition in lithium [14] [15] . The additional interest in the EEDF for the photo plasma is related to the light-to-electric signal conversion [16] [17] .
Two-photon excitation of Li(3d) state is a starting point for a variety of processes in lithium vapor. Under conditions of high atom densities (1015 cm‒3) and laser powers (106 W・cm‒2), this excitation plays an important role in laser plasma production [18] - [20] . Recently, Labazan and Milosevic [21] studied the processes which occurred in lithium vapor under two-photon excitation of the Li(3d) state at 639.1 nm. In their experiment they used a pulsed dye laser pumped with excimer laser to excite the Li(3d) level by two-photon absorption at 639.1 nm. Density of lithium vapor was in the range (1013 - 1014 cm‒3) and laser powers (105 - 106 W・cm‒2). The laser pulse duration was about 20 ns (FWHM), laser repetition rate was usually 5 Hz and the pulse energy was measured in the range 1 - 4 mJ at 639.1 nm. They had measured the radiation rates from lithium atomic states populated by two-photon excitation.
Theoretical modeling of alkali metal vapor ionization under resonant optical excitation was carried out in [22] - [25] . It was shown that there existed a competition of several ionization reactions: two-photon ionization of resonant states, associative resonant states, direct ionization by electron impact of the ground state, the resonant-state stepwise ionization by electron impact and photionization from high-lying excited states by resonance radiation.
More recently, Mahmoud et al. [26] presented a computational model to study the collisional ionization processes which occurred under 2s→2p excitation of lithium vapor excited with a nanosecond pulsed laser. Our interest in this work is primary to investigate the Electron Energy Distribution Function (EEDF) in lithium vapour excitation at 2s→3d two-photon resonance to determine conditions (namely lithium atom densities, laser energy, etc.) for the excitation processes because of its eventual importance in understanding ionization-guiding discharge experiments. This work studies two main subjects:
1) The influence of the ionization processes on the EEDF shape and the electron density in laser excited lithium by two-photon.
2) The dependence of EEDF and the ion density on the laser power and the lithium vapor density. In addition, we compare our results with that calculated by McGeoch [24] . The article is organized in the following way. In Section 2, we present theoretical model which includes the physical processes and the rate equations and the mathematical formula of the rate coefficients used to describe expected processes. In Section 3, we show our calculation results along with a discussion of various processes involved. Finally our conclusions are presented in Section 4.
2. The Theoretical Model of Laser Excited Lithium Vapour 2S→3D Transition
The energy level structure of lithium atom is well known [26] . Its low ionization potential provides little obstacles for multiphoton excitation and ionization. In the study of Labazan and Milosevic [21] Xe-Cl excimer laser pumped dye laser is used for the ionization of lithium vapor. Two photons at 639.1 nm will excite the lithium atom from the ground state 2S to the excited state 3D. Another 639.1 nm photon will ionize the lithium atom. The two-photon excitation rate 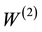 in (s‒1) can be written as:
in (s‒1) can be written as:
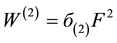 (1)
(1)
where 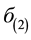 and F represent the two-photon excitation cross section and the photon flux density respectively. The photon flux is given by,
and F represent the two-photon excitation cross section and the photon flux density respectively. The photon flux is given by,
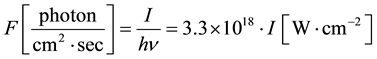
In this section, we consider the processes which occur in lithium vapour under two-photon excitation of the Li(3D) state at 639.1 nm. The molecular channel does not contribute to ionization processes according to the experimental conditions [20] [21] .
2.1. Process Considered
1) The absorption of resonant photon.
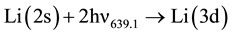
2) Photon ionization of the nl level.
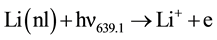
3) Associative ionization of 3d-3d collision.
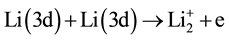
4) Collisional ionization (Penning ionization).
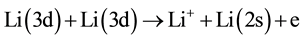
5) Reverse Energy pooling collisions.
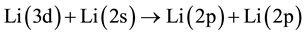
6) Radiative decay of Li(3d).
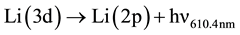
7) Energy pooling collisions.
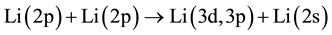
8) Super elastic collision (SEC):
The super elastic collision is described by the collision of a low energy electron with an excited atom. This process can be written as:
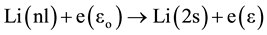 where ε > εo.
where ε > εo.
9) Electron impact excitation:
This process is the inverse of superelastic collision process,
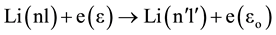 where ε > εo.
where ε > εo.
10) Electron impact ionization.
When an electron gains enough energy (through super-elastic collisions), which is equal to the ionization potential of the neutral atom, It can undergo an ionizing collision by electron impact process, resulting in a low energy electron of 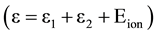 and atomic ion.
and atomic ion.
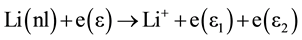
where 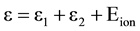 and
and ![]() is the ionization energy.
is the ionization energy.
11) Radiative recombination.
![]()
12) Three-body recombination.
![]()
where 3s ≤ nl ≤ 7d.
For simplicity we have assumed that ε1 = ε2 in the electron impact ionization and its inverse three-body recombination processes. There are several assumptions which we use for mathematical description of excitation and ionization processes.
2.2. Rate Equations
The rate of change of population density of state 2s, 2p, 3d and the highly excited states nl is given by,
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
The rate of growth of the molecular ion and the atomic ion is given by,
![]() (6)
(6)
![]() (7)
(7)
where,
![]() ,
,![]() ,
, ![]() and
and ![]() are the population density of levels 2s, 2p, 3d and nl, respectively.
are the population density of levels 2s, 2p, 3d and nl, respectively.
![]() represents the electron density as a function of electron energy
represents the electron density as a function of electron energy![]() .
.
![]() is the stimulated absorption rate coefficient from 2s to 3d level (sec−1).
is the stimulated absorption rate coefficient from 2s to 3d level (sec−1).
![]() is the stimulated emission rate coefficient from 3d to 2s level (sec−1).
is the stimulated emission rate coefficient from 3d to 2s level (sec−1).
![]() Einstein coefficient for spontaneous emission for the transition 2p to 2s (sec−1).
Einstein coefficient for spontaneous emission for the transition 2p to 2s (sec−1).
![]() Einstein coefficient for spontaneous emission for the transition (3d to 2s) (sec−1).
Einstein coefficient for spontaneous emission for the transition (3d to 2s) (sec−1).
![]() Einstein coefficient for spontaneous emission for the transition 3p to 2s (sec−1).
Einstein coefficient for spontaneous emission for the transition 3p to 2s (sec−1).
![]() Einstein coefficient for spontaneous emission for the transition 3d to 2p (sec−1).
Einstein coefficient for spontaneous emission for the transition 3d to 2p (sec−1).
![]() Einstein coefficient for spontaneous emission for the transition n→m (sec−1).
Einstein coefficient for spontaneous emission for the transition n→m (sec−1).
![]() represents the energy pooling collisions rate coefficient (cm3×sec−1).
represents the energy pooling collisions rate coefficient (cm3×sec−1).
![]() represents the reverse energy pooling collisions rate coefficient (cm3×sec−1).
represents the reverse energy pooling collisions rate coefficient (cm3×sec−1).
![]() represents the association ionization rate coefficient (cm3×sec−1).
represents the association ionization rate coefficient (cm3×sec−1).
![]() represents Penning ionization rate coefficient for level n (cm3×sec−1).
represents Penning ionization rate coefficient for level n (cm3×sec−1).
![]() represents the electron collision rate coefficient for transition from (3d→2s) as a function of electron energy
represents the electron collision rate coefficient for transition from (3d→2s) as a function of electron energy ![]() (cm3×sec−1).
(cm3×sec−1).
![]() represents the electron collision rate coefficient for transition from (2s→3d) as a function of electron energy
represents the electron collision rate coefficient for transition from (2s→3d) as a function of electron energy ![]() (cm3×sec−1).
(cm3×sec−1).
![]() represents electron collision ionization rate coefficient for level 3d (cm3×sec−1).
represents electron collision ionization rate coefficient for level 3d (cm3×sec−1).
![]() represents electron collision ionization rate coefficient for level 2s (cm3×sec−1).
represents electron collision ionization rate coefficient for level 2s (cm3×sec−1).
![]() represents electron collision ionization rate coefficient for level n (cm3×sec−1).
represents electron collision ionization rate coefficient for level n (cm3×sec−1).
![]() represents the electron collision rate coefficient for transition from (n→m) as a function of electron energy
represents the electron collision rate coefficient for transition from (n→m) as a function of electron energy ![]() (cm3×sec−1).
(cm3×sec−1).
![]() represents the electron collision rate coefficient for transition from (m→n) as a function of electron energy
represents the electron collision rate coefficient for transition from (m→n) as a function of electron energy ![]() (cm3×sec−1).
(cm3×sec−1).
![]() represents the photon ionization cross-section for level n (cm2).
represents the photon ionization cross-section for level n (cm2).
![]() represents the single photon ionization cross-section for level 2p (cm2).
represents the single photon ionization cross-section for level 2p (cm2).
![]() represents the three body recombination rate coefficient for level n (cm6×sec−1).
represents the three body recombination rate coefficient for level n (cm6×sec−1).
![]() represents the radiative recombination rate coefficient (cm3×sec−1).
represents the radiative recombination rate coefficient (cm3×sec−1).
![]() represents the density of atomic ions.
represents the density of atomic ions.
![]() represents the density of molecular ions.
represents the density of molecular ions.
![]() is the photon flux (photon/(cm2×sec)).
is the photon flux (photon/(cm2×sec)).
The electron energy distribution function equation (EEDF) is given by:
![]() (8)
(8)
The normalization conditions are given by:
![]() (9)
(9)
![]() (10)
(10)
where N0 is the density of Li atomic vapour. Note that the factor 1/2 with kEP and kAI corrects for possible double counting of each colliding pair of identical particles [27] .
2.3. Effects of EEDF on Collisional Rates
To calculate the electron energy distribution function, numerous data have to be compiled from the literature to be fed into the Boltzmann equation computational code [28] . By the use of suitable approximations for the energy dependence of the cross sections, the rate coefficients can be expressed by simple analytical formula. The rates of collisional process in plasma are given by the product of the plasma electron density ne and the rate coefficient ![]() of the particular process. The rate coefficient is determined by integrating an energy-depen- dent collision cross section б(ε) over the electron energy distribution function [29] .
of the particular process. The rate coefficient is determined by integrating an energy-depen- dent collision cross section б(ε) over the electron energy distribution function [29] .
![]() (11)
(11)
where v and ε are the velocity and energy, of the incident electron respectively. The lower limit of the integration is the threshold energy of the process for collisional excitation and ionization.
For single-temperature plasmas with Maxwellian electron energy distributions, de-excitation and recombination rates can be obtained directly from collisional excitation and ionization rate coefficients through detailed balance. For plasmas that have electrons in non-Maxwellian distributions, the cross sections of these reverse rates must be integrated over the entire electron energy distribution. By the use of suitable approximation for the energy dependence of the cross sections, the corresponding rate coefficients can be expressed by simple analytical formula.
The cross sections for excitation by electron impact ![]() are linearly approximated in the energy range of interest [29] :
are linearly approximated in the energy range of interest [29] :
![]() (12)
(12)
Here, Cnm is the excitation cross section constant and εs the energy threshold. The excitation rate coefficient is obtained by integration with respect to Maxwellian energy distribution:
![]() (13)
(13)
The rate coefficient kmn for the reverse reaction, superelastic collisions is obtained by the principle of detailed balance as follows:
![]() (14)
(14)
where gn and gm are the statistical weights of the upper and lower levels, respectively.
For the ionization of excited states by electron impact we use the empirical formula given by Vriens and Smeets [30] for the cross section and rate coefficients:
![]() (15)
(15)
where Ei = 5.18 − En ε ≥ Ei.
The reverse reaction, recombination by a three-particle collision, is obtained by the detailed balancing of ionization:
![]() (16)
(16)
where gn and g+ are the statistical weights of the neutral atomic and the atomic ion respectively.
For the radiative recombination rate coefficients we have used the empirical formula given by Drawin [31] :
![]() (17)
(17)
![]() (18)
(18)
and ux =1.58 ´ 105![]() , Z is the atomic number of the neutral atom and T is the gas temperature in K˚.
, Z is the atomic number of the neutral atom and T is the gas temperature in K˚.
On the other hand the values of the rate coefficients of collisional ionization, energy pooling collisions and processes in our model are indicated in Table 1.
3. Results and Discussion
The set of equations which was mentioned previously is solved numerically under the experimental conditions of Labazan and Milosevic [21] . In this instance the initial lithium vapor density was assumed to be 3 ´ 1013 - 7 ´ 1014 cm‒3, the laser power changes from 1 ´ 105 to 1 ´ 106 W・cm‒2, the temperature varied from 760 K˚ - 880 K˚
and the energy of single pulse (E) varied from 1→4 m Joule. The laser intensity (I) is given by![]() ,
,
![]()
Table 1. Kinetic processes in lithium ionization model.
where 𝜏 is the laser pulse duration and r is the laser beam radius. Under these conditions, the laser light was tuned to the two-photon resonance 2s→3d, at λ = 639.1 nm. The rate equation for the electron energy distribution function (8) is divided into 54 equations, where the ionization energy of Li = 5.39 eV and the energy step equal 0.1 eV. We calculate 1) the electron energy distribution function and its dependence on the laser intensity and lithium vapor density., 2) the effect of laser power and the time on the atomic ion (Li+) and the molecular ion![]() , 3) the effect of laser power and the lithium vapor density on the time evolution of the electron density which generated during the laser interaction with lithium vapor.
, 3) the effect of laser power and the lithium vapor density on the time evolution of the electron density which generated during the laser interaction with lithium vapor.
3.1. The Dependence of the Electron Energy Distribution Function on the Lithium Atomic Vapor and Laser Power
The electron energy distribution function as a function of lithium atomic vapor after 20 ns and laser power 1 ´ 105 W・cm−2 is plotted and shown in Figure 1. From this figure we note that the spectral structure is observed with certain peaks (A, B, C, D, and E) lying at energies 0.35, 1.1, 1.75, 2.5 and 3 eV respectively. The energy distribution of the electrons produced in peak A is centering at a mean energy E ≈ 0.35 eV by photon ionization processes which is described by the following equation.
![]()
Also the peak B corresponds to electrons produced by photon ionization processes of (5s, 4d, 4p, 4s).
![]()
While the peak C corresponds to single photon ionization.
![]()
Figure 1. The dependence of the Electron Energy Distribution Function on the lithium vapor density after 20 n sec from the laser pulse and laser power 1 × 105 W・cm−2.
![]()
The peak D corresponds to the electrons produced by Penning and associative ionization of Li(3d) which described by the following collision.
![]()
![]()
While the peak E is attributed to the superelastic collisions.
![]() where ε > εo.
where ε > εo.
We assume that the interaction started with the absorption of laser photons by Li(2s) excited to Li(3d) through two-photon resonance process. We assume that the most important source of population of the Li(3d) state is the laser excitation, atoms can make many interactions like Penning, associative ionization, photoionization, decay to Li(2p) (life time τ3d-2p = 16.7 ns [20] , may collide with Li(2s) in reverse energy pooling reaction to form Li(2p) atoms which is the main source of highly excited atoms through energy pooling interactions, also Li(3d) atoms may collide with Li(2s) to create Li(3p) through energy transfer collisions [21] , finally super elastic collisions and photoionization processes of all excited states can take place during the interaction.
The dependence of the electron energy distribution function on the laser power after 20 ns and lithium vapor density 3 ´ 1013 cm−3 is indicated in Figure 2. From this figure we show that, as the laser power increases, the
![]()
Figure 2. Electron Energy Distribution Function after 20 n sec from the laser pulse at different values of laser power and lithium vapor density 3 × 1013 cm−3.
value of the electron energy distribution increases at EEDF corresponding to peaks, B, C and E. This result indicates the dependence of the occurrence of some physical processes on the laser power which turn results in the appearance of such peaks in EEDF. These peaks are attributed to some physical processes which contribute to the population and depopulation of the various excited states considered in this analysis. The figures illustrates the role of the photoioniation process in EEDF formation in the case when Jph is for an order of magnitude greater than the ionization flux due to electron impact Jei = kc,2pN(2p)ne. Photoionization from the Li (3P) and Li(3d) states produces electrons with energy ~0.3 eV. As one can see, a peak is formed on EEDF around this energy. However the interesting point from our point of view is that, the photoionization and collisional ionization are the dominant processes during the plasma formation in laser excited lithium atoms [15] [16] .
3.2. The Dependence of the Atomic Ions (Li+) Density on the Atomic Lithium Vapor and Laser Power
The growth rate of the atomic ions (Li+) density as a function of lithium vapor density is shown in Figure 3 for different values of irradiation time. From this figure it can be seen that the atomic ions (Li+) density show that as the lithium density increases the ion density Li+ increases and the curves show almost the same behavior with descending values of lithium vapor density for different values of time. Also it is observed that the density of atomic ions (Li+) increases with the laser power as indicates in Figure 4 for different values of time. This beha- vior is due to the Li+ mainly produced by the photoionization and laser induced Penning ionization processes
![]()
Figure 3. Variation of Atomic ions density Li+ with Lithium vapor density No at different time intervals and laser power 1 × 105 W・cm−2.
[17] . Collisions of highly-excited atoms with resonantly excited ones may result in Penning ionization where nl states are populated in energy pooling collisions of two Li(2p) atoms [21] .
3.3. The Time Evolution of the Atomic Ion Li+
The growth rate of the Li+ as a function of time is indicated in Figure 5 for different values of laser power. From this figure it can be seen that the (Li+) shows a fast increase during the early stages of the interaction up to 5 ns followed by a linear increase up to 10 ns. Immediately after this time the density of Li+ density shows a slow increase during the late stage of the irradiation time. This behavior is due to the Li+ mainly produced by the Penning ionization and photionization processes as follows:
![]()
![]()
where nl states are populated in energy pooling collisions of two Li(3d) atoms:
![]()
In general the figure shows the same behavior for almost values of the irradiation time.
3.4. The Molecular ions ![]() Density as a Function of Lithium Vapor Density
Density as a Function of Lithium Vapor Density
Density of the molecular ions ![]() variation with lithium vapor density is illustrated in Figure 6 at laser power 1 × 105 W・cm‒2. From this figure we can see that the Li2+ density increases rapidly with increasing of
variation with lithium vapor density is illustrated in Figure 6 at laser power 1 × 105 W・cm‒2. From this figure we can see that the Li2+ density increases rapidly with increasing of
![]()
Figure 4. Variation of Atomic ions density Li+ with laser power at different time intervals and lithium vapour density 7 × 1014 cm−3.
lithium vapor density, while the density of molecular ions is approximately constant with the variation of laser power where the molecular ions are produced from associative ionization (AI). On the hand, in lithium unlike the rest of the alkali metals, the reaction of the association ionization of two resonant excited atoms is not important at T (gas temperature) < 0.1 eV, due to a considerable energy deficit (~0.7 eV) which diminishes its efficiency [16] .
3.5. The Time Evolution of the Molecular Ion ![]()
The growth rate of the molecular ion ![]() as a function of time is illustrated in Figure 7 for different values of laser power. From this figure, we can see that the
as a function of time is illustrated in Figure 7 for different values of laser power. From this figure, we can see that the ![]() density shows a fast increase during the period 0.1 ns up to 5 ns followed by a linear increase up to 20 ns. Immediately after this time the Li+2 density shows a slow increase during the late stages of the irradiation time. An understanding of this behavior can be attained by considering that the main processes for producing these molecular ions are associative ionization (AI) process as follows:
density shows a fast increase during the period 0.1 ns up to 5 ns followed by a linear increase up to 20 ns. Immediately after this time the Li+2 density shows a slow increase during the late stages of the irradiation time. An understanding of this behavior can be attained by considering that the main processes for producing these molecular ions are associative ionization (AI) process as follows:
![]() (AI)
(AI)
where eV is the kinetic energy of the free electrons emitted when ![]() ion formed in the mean relative kinetic energy of the colliding atoms in the beam. Generally, the linear shape of
ion formed in the mean relative kinetic energy of the colliding atoms in the beam. Generally, the linear shape of ![]() and the linear and quadratic term exchange show that the only possible mechanism for producing the molecular ion is (AI) at a certain density of Li atomic vapor.
and the linear and quadratic term exchange show that the only possible mechanism for producing the molecular ion is (AI) at a certain density of Li atomic vapor.
![]()
Figure 5. Time evolution of Atomic ion Li+ at different lithium vapor densities and laser power 1 × 105 W・cm−2.
![]()
Figure 6. Variation of molecular ion density Li2+ with Lithium vapor density No at different time intervals and laser power 1 × 105 W・cm−2.
![]()
Figure 7. Time evolution of Molecular ion ![]() at different lithium vapor densities and laser power 1 × 105 W・cm−2.
at different lithium vapor densities and laser power 1 × 105 W・cm−2.
3.6. The Dependence of the Electron Density (Ne ) on the Atomic Lithium Vapor and Laser Power
Variation of electrons density with lithium vapor density is shown in Figure 8, the curves show that Ne is directly proportional to the lithium vapor at laser power 1 × 105 W・cm−2. Also Figure 9 shows the dependence of the electron density of the laser power at constant lithium vapor density. From this figure, we note that as the laser increases the density of the electron Ne increases and the curves show the same behavior with descending values of the laser power for the different periods of irradiation time. Moreover, at high laser power greater than 105 W・cm−2 we note a very fast increase in the electron density. The explanation of this behavior is attributed to the main physical processes which produce the Ne are the photoionization and collisional ionization processes. On the other hand under the resonant radiation the ionization goes from Li(3p), Li(3d) and also from the higher lying states, the photoionization flux from the kth level ![]() is proportional to the ionization cross section
is proportional to the ionization cross section![]() , to the level population nk and to the photon flux density
, to the level population nk and to the photon flux density![]() ,where I (W・cm−2) is the incident radiation density. For the conditions under consideration one can expect the maximal population for the states situated near resonant excited Li(3d) level, which is why the total ionization rate is determined by the ionization from Li(3p) and Li(3d) states. The energy gap between these two levels is 0.045 eV.
,where I (W・cm−2) is the incident radiation density. For the conditions under consideration one can expect the maximal population for the states situated near resonant excited Li(3d) level, which is why the total ionization rate is determined by the ionization from Li(3p) and Li(3d) states. The energy gap between these two levels is 0.045 eV.
3.7. The Time Evolution of the Electron Density Ne
The growth rate of electrons Ne as a function of time is indicted in Figure 10 for different values of lithium vapor density. From this figure, we can see that, the electron density increase up to 20 ns. Immediately after this time the electron density shows a slow increase during the late stages of the interaction. The explanation of the linear growth can be described as follows, after the absorption of two-photon resonance,
![]()
ions can be created by following paths.
The first is a photoionization of the 3d level:
![]()
The second path is reverse energy pooling or spontaneous decay of Li(3d) to form Li(2p) followed by energy pooling of Li(2p) atoms to form higher excited states like (3d, 3p, …) level followed by photoionization:
![]()
![]()
Figure 8. Variation of electrons density Ne with Lithium vapor density No at different time intervals and laser power 1 × 105 W・cm−2.
![]()
![]()
![]()
The third one is Penning ionization: ![]()
In general, during the early stages electrons are created at a high rate through photoionization and collisional ionization processes. Beyond this time, the growth rate of the atomic ion becomes slower due to the competition between the generation of the electrons through Penning ionization or photoionization, as well collisional of the ground and excited losses of the ions by radiative recombination and three body recombination [20] [21] . In contrast, photoionization can play a remarkable role at a low ionization degree of the medium, when the basic mechanism of the Li(3p,3d) population are energy pooling collisions: ![]() [39] . Through this process electron excitation prevails when kEPN(2p) > k 2p-(3p,3d) ne where kEP is the energy pooling rate coefficient. As far as we know, there is no definite value for this constant for lithium. The considered reaction is an endothermic one. For the pooling reaction with resonant Cs atoms a similar energy gap (∆Ep ~0.18 eV) the reaction constants are of an order kEP ~(10−11 - 10−12) cm3・s‒1 [40] . When we employ this value to
[39] . Through this process electron excitation prevails when kEPN(2p) > k 2p-(3p,3d) ne where kEP is the energy pooling rate coefficient. As far as we know, there is no definite value for this constant for lithium. The considered reaction is an endothermic one. For the pooling reaction with resonant Cs atoms a similar energy gap (∆Ep ~0.18 eV) the reaction constants are of an order kEP ~(10−11 - 10−12) cm3・s‒1 [40] . When we employ this value to
![]()
Figure 9. Variation of electrons density Ne with laser power at different time intervals and lithium vapor density 3 × 1013 cm−3.
make estimations for the reaction with lithium we find that under optical saturation potoionization processes can be the dominant processes in ionization processes.
Similarly, energy pooling collisions play a dual role as they deplete the lower states and simultaneously populate the upper states of interest, thus doubling the effect. In fact the two process, (superelastic transfer to the free electrons and energy pooling collisions) work in tandem to create qusicontinuous population inversions.
To give a deeper understanding of the role played by the physical processes in the electron growth rate and to confirm these results we compared our relation with that which obtained by McGeoch [24] . He applied his simple kinetic model of optically pumped lithium plasma to calculate the time evolution of the electron density which created during the interaction of lithium vapor with laser radiation. From Figure 11 it is seen that our results showed the same trend as those calculated by McGeoch [24] , where their values display reasonable consistency over the whole range time. This in turn verified the validity of the model to investigate the Electron energy distribution function (EEDF) in lithium vapor excitation at 2s→3d two-photon resonance.
4. Conclusion
We have carried out a computational study of the influence of collisional ionization and collisional excitation processes which occur in lithium vapour under two-photon excitation of the Li(3d) state at 639.1 nm. We have
![]()
Figure 10. Time evolution of electrons density Ne at different lithium vapor densities and laser power 1 × 105 W・cm−2.
![]()
Figure 11. Comparison between the calculated Electron density of our model and that obtained by McGeoch [24] model at Laser pulse = 20 ns and lithium vapor density Li = 1 × 1013 cm−3.
calculated the electron energy distribution function as well as the molecular ions and atomic ions for lithium atom densities in the range (1013 - 1014 cm−3) and laser powers (105 - 106 W・cm−2). The results confirm a satisfactory description of the experimentally observed behavior. At atomic density of 1014 cm−3 radiation population of the Li(2p) state dominates over the collisional energy transfer (REP). The reverse energy pooling as a source for large pool of Li(2p) atoms could be important at large atom densities. The nonlinear dependence of the electron energy distribution function on the lithium vapor density indicates that collisional processes, such as laser induced Penning ionization, associative ionization, Photoionization, as well as energy pooling collisions (which play role in populating the 3p and 3d states) form the plasma. The high energy of the EEDF had a non-equili- brium shape. This was caused by relaxation of fast electrons produced by super-elastic collisions with residual excited atoms. The model may be useful in a laser induced plasma or discharge experiments.