Quasi-Radial Modes of Pulsating Neutron Stars: Numerical Results for General-Relativistic Rigidly Rotating Polytropic Models ()
1. Introduction
According to “Hartle’s perturbation method” (also called “Hartle-Thorne perturbation method”; [1] [2] ), we treat rotating relativistic neutron stars as perturbative solutions of the Einstein’s field equations, which describe a static spherically symmetric relativistic model. Our aim here is to compute, based on the work of Hartle et al. [3] and also of Hartle and Friedmann [4] , the zerothand second-order eigenfrequencies of the lowest three modes of radial pulsation for general-relativistic polytropic models. The zeroth-order eigenfrequencies,  , are the eigenfrequencies of the nonrotating model, while the second-order ones,
, are the eigenfrequencies of the nonrotating model, while the second-order ones,  , are the rotationinduced changes in the eigenfrequencies.
, are the rotationinduced changes in the eigenfrequencies.
In this study, we use “gravitational units” (abbreviated “gu”; see [5] and [6] ), also called “geometrized units”. In these units the speed of light,  , and the gravitational constant,
, and the gravitational constant,  , are equal to unity,
, are equal to unity,  , and the length is the unique “base unit”, measured in centimeters (abbreviated “cm”). On the other hand, the wellknown “centimeter-gram-second units” (abbreviated “
, and the length is the unique “base unit”, measured in centimeters (abbreviated “cm”). On the other hand, the wellknown “centimeter-gram-second units” (abbreviated “ ”) have three base units: the length measured in cm, the mass measured in grams (abbreviated “
”) have three base units: the length measured in cm, the mass measured in grams (abbreviated “ ”), and the time measured in seconds (abbreviated “
”), and the time measured in seconds (abbreviated “ ”).
”).
2. The Nonrotating Model
The Schwarzschild metric for a nonrotating spherical object, expressed in polar coordinates, is given by the relation ([1] , Equation (25))
 (1)
(1)
where  and
and  are metric functions of
are metric functions of . The exponential functions
. The exponential functions  and
and  represent the fluctuations in the time rate flow and the divergence from the Euclidean geometry, respectively. The gravitational potential
represent the fluctuations in the time rate flow and the divergence from the Euclidean geometry, respectively. The gravitational potential  is usually defined as (see e.g. [5] , Equation (2))
is usually defined as (see e.g. [5] , Equation (2))
 (2)
(2)
and the metric function  by (see e.g. [5] , Equation (5))
by (see e.g. [5] , Equation (5))
 (3)
(3)
where  is the mass-energy of the star.
is the mass-energy of the star.
A relativistic neutron star obeys the Tolman-Oppenheimer-Volkoff (TOV) equations of (i) hydrostatic equilibrium ([1] , Equation (28))
 (4)
(4)
and (ii) mass-energy ([1] , Equation (29a))
 (5)
(5)
fulfilling the initial conditions
 (6)
(6)
where  is the pressure and
is the pressure and  the mass-energy density.
the mass-energy density.
To treat numerically the system (4)-(5), we need an equation relating  to
to ,
,  , that is, an “equation of state” (EOS). In this study, we consider the polytropic EOS (see e.g. [7] , Equation (3); see also [8] , Section II)
, that is, an “equation of state” (EOS). In this study, we consider the polytropic EOS (see e.g. [7] , Equation (3); see also [8] , Section II)
 (7)
(7)
The parameters  and
and  are the so-called “polyropic constant” and “polytropic index”, respectively. The so-called “adiabatic index”,
are the so-called “polyropic constant” and “polytropic index”, respectively. The so-called “adiabatic index”,  , is defined as (cf. [3] , Equation (2.3))
, is defined as (cf. [3] , Equation (2.3))
 (8)
(8)
and, in general, is associated with perturbations about equilibrium under constant entropy. On the other hand, the so-called “adiabatic index associated with the equation of state”,  , is defined as (cf. [3] , Equation (3.12))
, is defined as (cf. [3] , Equation (3.12))
 (9)
(9)
In the polytropic EOS (7),  is the rest-mass density, related to the mass-energy density via the equation ([6] , Equation (9))
is the rest-mass density, related to the mass-energy density via the equation ([6] , Equation (9))
 (10)
(10)
To solve the system (4)-(5), we write the two equations as ([6] , Equations (8) and (9), respectively)
 (11)
(11)
 (12)
(12)
The initial conditions are now
 (13)
(13)
To complete the study of the nonrotating model, we need to solve the differential equation for the gravitational potential  ([1] , Equation (29b))
([1] , Equation (29b))
 (14)
(14)
obeying the boundary condition at the surface of the star (cf. [6] , Equation (30))
 (15)
(15)
3. Rigid Rotation
When a star is rotating, its shape deviates from sphericity. Furthermore, when the star is in equilibrium state, there is a balance between the pressure forces, the gravitational forces, and the centrifugal forces. Assuming that the star is rotating rigidly and slowly (see however the starting remark in Section 7), the perturbed metric is given by ([2] , Equation (4))
 (16)
(16)
where  are Legendre polynomials; the perturbation functions
are Legendre polynomials; the perturbation functions ,
,  ,
,  ,
,  , and
, and  are radial functions proportional to
are radial functions proportional to ; the centrifugal forces depend on the angular velocity
; the centrifugal forces depend on the angular velocity  relative to a distant observer, as well as on the angular velocity
relative to a distant observer, as well as on the angular velocity  relative to the local inertial frame, these two angular velocities connected via the relation ([2] , Equation (6))
relative to the local inertial frame, these two angular velocities connected via the relation ([2] , Equation (6))
 (17)
(17)
where  is the angular velocity of the local inertial frame. To calculate
is the angular velocity of the local inertial frame. To calculate , we solve the so-called “framedragging equation” ([2] , Equation (9))
, we solve the so-called “framedragging equation” ([2] , Equation (9))
 (18)
(18)
where ([2] , Equation (10))
 (19)
(19)
Outside the star,  takes the form ([2] , Equation (13b))
takes the form ([2] , Equation (13b))
 (20)
(20)
where  is the total angular momentum of the star, given by ([2] , Equation (13a))
is the total angular momentum of the star, given by ([2] , Equation (13a))
 (21)
(21)
where  is the radius of the star.
is the radius of the star.
To solve Equation (18), we integrate from the center of the star outwards, imposing the initial conditions
 (22)
(22)
where the constant  is chosen arbitrarily. Since, due to Equation (20), the angular velocity
is chosen arbitrarily. Since, due to Equation (20), the angular velocity  corresponding to the arbitrarily chosen initial value
corresponding to the arbitrarily chosen initial value 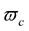 is equal to
is equal to
 (23)
(23)
and since, in general, the prescribed angular velocity  is different to
is different to , we must rescale the solution
, we must rescale the solution  of Equation (18) in order for the prescribed value
of Equation (18) in order for the prescribed value  to be applied to our model (for details on this matter, see [5] , Section 5.2),
to be applied to our model (for details on this matter, see [5] , Section 5.2),
 (24)
(24)
4. Spherical Deformation
The spherical deformations due to rigid rotation are the mass perturbation function,  , and the pressure perturbation function,
, and the pressure perturbation function, . They are calculated by integrating the “
. They are calculated by integrating the “ equations of hydrostatic equilibrium” ([1] , Section VII), which become after a long algebra ([2] , Equations (15a) and (15b), respectively)
equations of hydrostatic equilibrium” ([1] , Section VII), which become after a long algebra ([2] , Equations (15a) and (15b), respectively)
 (25)
(25)
 (26)
(26)
with initial conditions  and
and  at
at .
.
The perturbation function  (to be used in Section 5), involved in the metric (16), is defined outside the star as ([2] , Equation (17a))
(to be used in Section 5), involved in the metric (16), is defined outside the star as ([2] , Equation (17a))
 (27)
(27)
and inside the star as ([2] , Equation (17b))
 (28)
(28)
The constant  is determined so that
is determined so that  be continuous across the surface (see e.g. [5] , Equation (47))
be continuous across the surface (see e.g. [5] , Equation (47))
 (29)
(29)
In these equations,  is the mass-energy of the star (also called gravitational mass); and
is the mass-energy of the star (also called gravitational mass); and  is the increase in the gravitational mass due to spherical deformation, given by ([5] , Equation (43))
is the increase in the gravitational mass due to spherical deformation, given by ([5] , Equation (43))
 (30)
(30)
5. Quasi-Radial Pulsation
When a star is rotating rigidly with a small angular velocity  (see however the starting remark in Section 7), the squared eigenfrequencies
(see however the starting remark in Section 7), the squared eigenfrequencies  of its pulsation modes can be expanded in powers of
of its pulsation modes can be expanded in powers of  ([4] , Equation (2.1)),
([4] , Equation (2.1)),
 (31)
(31)
where the superscript “ ” denotes terms of zeroth order in
” denotes terms of zeroth order in , and the superscript “(2)” terms of second order in
, and the superscript “(2)” terms of second order in . The aim of the present study is to compute the zerothand the second-order eigenfrequencies of the lowest three pulsation modes.
. The aim of the present study is to compute the zerothand the second-order eigenfrequencies of the lowest three pulsation modes.
Concerning the zeroth-order eigenfrequencies, we begin with the so-called “Chandrasekhar operator” ([3] , Equation (4.6b)),  , applied to the so-called “displacement function” ([3] , Equations (4.2a, b, c, d)),
, applied to the so-called “displacement function” ([3] , Equations (4.2a, b, c, d)),  , and set equal to zero,
, and set equal to zero,
 (32)
(32)
where primes denote differentiation with respect to , and
, and
 (33)
(33)
 (34)
(34)
 (35)
(35)
 (36)
(36)
 (37)
(37)
 (38)
(38)
The second-order differential Equation (32), subject to the initial condition ([3] , Equation (4.2e))
 (39)
(39)
(without loss of generality, we can take ) and to the boundary condition
) and to the boundary condition
 (40)
(40)
establishes a Sturm-Liouville (SL) boundary value problem with eigenvalues the pulsation eigenfrequencies
 . Equation (32) can be put into the so-called “SL form” (cf. [9] , Equation (14))
. Equation (32) can be put into the so-called “SL form” (cf. [9] , Equation (14))
 (41)
(41)
where
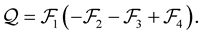 (42)
(42)
The SL form (41) can be transformed into a system of two first-order differential equations ([9] , Equations (18) and (19)),
 (43)
(43)
subject to the initial conditions  and
and  near
near , and to the boundary condition
, and to the boundary condition  at the surface (Equation (40)).
at the surface (Equation (40)).
To compute the eigenvalue(s) , we work as follows. We start the numerical integration for a trial value
, we work as follows. We start the numerical integration for a trial value  and initial conditions as above. We integrate towards the surface and then check if the resulting solution
and initial conditions as above. We integrate towards the surface and then check if the resulting solution  satisfies the boundary condition
satisfies the boundary condition . From the point of view of numerical analysis, this boundary condition can be treated as an algebraic equation of the form
. From the point of view of numerical analysis, this boundary condition can be treated as an algebraic equation of the form ; thus our task, to compute the root(s)
; thus our task, to compute the root(s)  of this equation, can be achieved by a standard numerical method (e.g. the bisection method).
of this equation, can be achieved by a standard numerical method (e.g. the bisection method).
The second-order eigenfrequencies  are computed by the relation ([3] , Equation (4.8))
are computed by the relation ([3] , Equation (4.8))
 (44)
(44)
The driving term  is defined as (cf. [3] , Table 4)
is defined as (cf. [3] , Table 4)

(45)
where, in turn,

(46)
 (47)
(47)
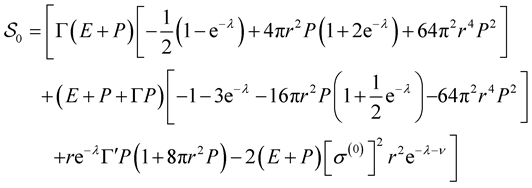 (48)
(48)
 (49)
(49)
 (50)
(50)
and
 (51)
(51)
6. The Computations
In this study, to compute nonrotating models (Section 2), rigid rotations (Section 3), and spherical deformations (Section 4), we use the corresponding numerical methods described in very detail in [5] (Sections 5.1 and 5.2). We then combine these methods with the numerical framework described in Section 5 for computing the zerothand second-order eigenfrequencies of pulsation.
To implement all the required methods, and thus to compute the results presented here, we have written and used a Mathematica® program.
7. Numerical Results and Discussion
To begin with, it is worth remarking here that, as it has been verified by several authors (see e.g. [10] , Sections 4 and 7; see also [11] , Section 5.3; for differentially rotating neutron stars, see [5] , Section 6), Hartle’s perturbation method gives remarkably accurate results even when applied to rapidly rotating neutron stars, although this method has been developed as a slow-rotation perturbation method.
As discussed in [4] (Section I), pulsars are identified as rotating neutron stars and, therefore, there is a strong interest in studying the influence of a rigid rotation on the properties of such relativistic objects. In particular, it is of great interest to compute the pulsation frequencies of the quasi-radial modes (i.e. modes which would be radial in the absence of rotation) for several models and thus to have a measure of the effect of general relativity on these frequencies. To that purpose, we have computed, and present in this section, relevant numerical results.
Regarding our computations, we resolve four nonrotating general-relativistic polytropic models with polytropic indices  and
and . Each model is resolved for five central mass-energy densities:
. Each model is resolved for five central mass-energy densities: ,
,  ,
,  ,
,  , and
, and  cgs. These values have been chosen to be below and relatively close to the “maximum-mass densities” of the corresponding models, being in fact the more interesting ones when considering neutron stars. It is worth mentioning here that the total mass
cgs. These values have been chosen to be below and relatively close to the “maximum-mass densities” of the corresponding models, being in fact the more interesting ones when considering neutron stars. It is worth mentioning here that the total mass  of a model, treated as a function of the central density
of a model, treated as a function of the central density ,
,  , obtains a maximum value
, obtains a maximum value  for a specific value
for a specific value ; such a model is called “maximum-mass model”, and the central density of this model is called “maximum-mass density”. The maximum-mass densities of our models, computed by a method described in [6] (Section 4), are
; such a model is called “maximum-mass model”, and the central density of this model is called “maximum-mass density”. The maximum-mass densities of our models, computed by a method described in [6] (Section 4), are ,
,  ,
,  and
and  cgs, respectively ([6] , Tables 2-5, respectively). All models, studied here, have
cgs, respectively ([6] , Tables 2-5, respectively). All models, studied here, have  cgs. Accordingly, in our computations the sequence of central mass-energy densities is terminated at
cgs. Accordingly, in our computations the sequence of central mass-energy densities is terminated at  cgs.
cgs.
Next, each density case is resolved for the three lowest modes of pulsation: Mode 0, Mode 1, and Mode 2. For each mode, we compute a rigidly rotating configuration with angular velocity equal to the corresponding Keplerian angular velocity, . Hartle’s perturbation method uses proper expansions in the rotation parameter
. Hartle’s perturbation method uses proper expansions in the rotation parameter
 , where
, where  is the angular velocity for which mass shedding starts occuring at the equator of a star. Thus
is the angular velocity for which mass shedding starts occuring at the equator of a star. Thus  describes the Newtonian balance between centrifugal and gravitational forces. However, this Newtonian upper bound appears to be a rather overestimated limit for neutron stars. For such relativistic objects, the appropriate upper bound is
describes the Newtonian balance between centrifugal and gravitational forces. However, this Newtonian upper bound appears to be a rather overestimated limit for neutron stars. For such relativistic objects, the appropriate upper bound is . Hence, if the angular velocity is slightly greater than
. Hence, if the angular velocity is slightly greater than , then mass shedding occurs at the equator of a neutron star.
, then mass shedding occurs at the equator of a neutron star.  can be computed by several methods (for a discussion on this matter, see [11] ; for a detailed description of such a method, see [12] ; see also [13] , and references therein, for results concerning general-relativistic polytropic models). In this study, the Keplerian angular velocities given in Tables 1-4 have been computed by using the well-known “Rotating Neutron Stars Package” (RNS) [14] .
can be computed by several methods (for a discussion on this matter, see [11] ; for a detailed description of such a method, see [12] ; see also [13] , and references therein, for results concerning general-relativistic polytropic models). In this study, the Keplerian angular velocities given in Tables 1-4 have been computed by using the well-known “Rotating Neutron Stars Package” (RNS) [14] .
Furthermore, we assume that the adiabatic indices  (Equation (8)) and
(Equation (8)) and  (Equation (9)) do coincide for the polytropic models under consideration,
(Equation (9)) do coincide for the polytropic models under consideration,
 (52)
(52)

Table 1. Central mass-energy density and rest-mass density, gravitational mass, and radius of a nonrotating general-relativistic polytropic model with polytropic index  and polytropic constant
and polytropic constant  . The Keplerian angular velocities, appearing here, have been computed by RNS.
. The Keplerian angular velocities, appearing here, have been computed by RNS.

Table 2. Central mass-energy density and rest-mass density, gravitational mass, and radius of a nonrotating general-relativistic polytropic model with polytropic index  and polytropic constant
and polytropic constant  . The Keplerian angular velocities, appearing here, have been computed by RNS.
. The Keplerian angular velocities, appearing here, have been computed by RNS.

Table 3. Central mass-energy density and rest-mass density, gravitational mass, and radius of a nonrotating general-relativistic polytropic model with polytropic index  and polytropic constant
and polytropic constant  . The Keplerian angular velocities, appearing here, have been computed by RNS.
. The Keplerian angular velocities, appearing here, have been computed by RNS.

Table 4. Central mass-energy density and rest-mass density, gravitational mass, and radius of a nonrotating general-relativistic polytropic model with polytropic index  and polytropic constant
and polytropic constant  . The Keplerian angular velocities, appearing here, have been computed by RNS.
. The Keplerian angular velocities, appearing here, have been computed by RNS.
In addition, a second step towards simplification is to assume, as several authors do (see e.g. [4] ; for a different view, on the other hand, see e.g. [9] ), that  is associated with the polytropic index
is associated with the polytropic index  via the polytropic relation (cf. [6] , Equation (5))
via the polytropic relation (cf. [6] , Equation (5))
 (53)
(53)
In all tables of the present paper, parenthesized (positive or negative) integers following numerical values denote powers of ten. For example, the entry  is equal to
is equal to  and the entry
and the entry  is equal to
is equal to .
.
For the five density cases with polytropic index , we can compare our results in Table 5 with respective results in Table 3 of [4] . To the purpose of such comparisons, we have written Table 5 in exactly the same format with that of Table 3 of [4] . We find excellent agreement between respective results, except for two eigenfrequencies
, we can compare our results in Table 5 with respective results in Table 3 of [4] . To the purpose of such comparisons, we have written Table 5 in exactly the same format with that of Table 3 of [4] . We find excellent agreement between respective results, except for two eigenfrequencies  belonging to Mode 2. The first one arises when
belonging to Mode 2. The first one arises when  and leads to a difference ~4% (our result is “−15.95”, while the result in [4] is “−16.6”); and the second one occurs when
and leads to a difference ~4% (our result is “−15.95”, while the result in [4] is “−16.6”); and the second one occurs when  and leads to a difference
and leads to a difference  (our result is “−14.15”, while that in [4] is “−13.7”). Since all other results do almost coincide, it seems that these two differences are of rather minor significance.
(our result is “−14.15”, while that in [4] is “−13.7”). Since all other results do almost coincide, it seems that these two differences are of rather minor significance.
Our main remarks on the numerical results presented in Tables 5-8 have as follows. First, in all cases examined, the eigenfrequencies  and
and  increase in absolute value with the central density. Equivalently, since (for the cases examined) increasing central density implies increasing gravitational mass, all the eigenfrequencies increase in absolute value with the gravitational mass. In addition, since increasing central density does also imply increasing Keplerian angular velocity for a rotating configuration, all the eigenfrequencies
increase in absolute value with the central density. Equivalently, since (for the cases examined) increasing central density implies increasing gravitational mass, all the eigenfrequencies increase in absolute value with the gravitational mass. In addition, since increasing central density does also imply increasing Keplerian angular velocity for a rotating configuration, all the eigenfrequencies  increase in absolute value with the Keplerian angular velocity.
increase in absolute value with the Keplerian angular velocity.

Table 5. Eigenfrequencies of the lowest three modes of a nonrotating and a rotating general-relativistic polytropic model with polytropic index , and polytropic constant and Keplerian angular velocities as in Table2
, and polytropic constant and Keplerian angular velocities as in Table2

Table 6. Eigenfrequencies of the lowest three modes of a nonrotating and a rotating general-relativistic polytropic model with polytropic index , and polytropic constant and Keplerian angular velocities as in Table1
, and polytropic constant and Keplerian angular velocities as in Table1

Table 7. Eigenfrequencies of the lowest three modes of a nonrotating and a rotating general-relativistic polytropic model with polytropic index , and polytropic constant and Keplerian angular velocities as in Table3
, and polytropic constant and Keplerian angular velocities as in Table3

Table 8. Eigenfrequencies of the lowest three modes of a nonrotating and a rotating general-relativistic polytropic model with polytropic index , and polytropic constant and Keplerian angular velocities as in Table4
, and polytropic constant and Keplerian angular velocities as in Table4
Second, all eigenfrequencies  are positive, thus representing stable nonrotating pulsating configurations. Likewise, the eigenfrequencies
are positive, thus representing stable nonrotating pulsating configurations. Likewise, the eigenfrequencies  are positive for Mode 0 and for the soft polytropic EOSs
are positive for Mode 0 and for the soft polytropic EOSs  and
and . Consequently, the effect of rotation is to stabilize such rotationally perturbed configurations. On the other hand, the eigenfrequencies
. Consequently, the effect of rotation is to stabilize such rotationally perturbed configurations. On the other hand, the eigenfrequencies  are negative for Modes 1 and 2 of the soft EOSs
are negative for Modes 1 and 2 of the soft EOSs
 and
and , as well as for the three modes of the stiff EOSs
, as well as for the three modes of the stiff EOSs  and
and , thus turning to destabilize the corresponding rotating configurations. It is worth mentioning here that, among the members of a collection of EOSs, the EOS deriving the larger value
, thus turning to destabilize the corresponding rotating configurations. It is worth mentioning here that, among the members of a collection of EOSs, the EOS deriving the larger value  for a given
for a given  is the “stiffest” EOS in the collection; while the EOS leading to the smaller value
is the “stiffest” EOS in the collection; while the EOS leading to the smaller value  for the same
for the same  is the “softest” EOS in this collection. Note that, for increasing polytropic index
is the “softest” EOS in this collection. Note that, for increasing polytropic index , the polytropic EOSs are getting softer; equivalently, for decreasing
, the polytropic EOSs are getting softer; equivalently, for decreasing , the polytropic EOSs become stiffer.
, the polytropic EOSs become stiffer.
Finally, in all cases examined, the zeroth-order eigenfrequencies  are ~one order of magnitude greater than the respective squared Keplerian angular velocities
are ~one order of magnitude greater than the respective squared Keplerian angular velocities ; this inequality is in fact a necessary condition for the perturbation theory developed in [3] and [4] to be valid, as discussed in detail in [4] (Section II). Consequently, all the cases examined lie within the domain of applicability of the theory, and, especially, of Equation (31) for computing the second-order eigenfrequencies
; this inequality is in fact a necessary condition for the perturbation theory developed in [3] and [4] to be valid, as discussed in detail in [4] (Section II). Consequently, all the cases examined lie within the domain of applicability of the theory, and, especially, of Equation (31) for computing the second-order eigenfrequencies  which represent the rotationally induced changes in the pulsation eigenfrequencies.
which represent the rotationally induced changes in the pulsation eigenfrequencies.